露天煤矿工程轮胎温度变化的有限元分析计算
李洪波,王跃旭
(1.神华北电胜利能源有限公司设备维修中心生产技术部,内蒙古 锡林浩特 026000;2.神华北电胜利能源有限公司机电信息部,内蒙古 锡林浩特 026000)
0 引 言
轮胎材料的力学性能会受到温度变化的影响,当轮胎的力学性能发生变化时,轮胎的强度及刚度也会发生相应的变化,最终使得轮胎的结构发生破损。温度的分布影响轮胎的转向、加减速及防滑等性能,如果轮胎的内部温度达到轮胎橡胶材料所能承载的最高温度橡胶材料也会因轮胎温度过高而损坏。在早期人们利用实验的方法来对滚动轮胎的生热问题进行研究,在进行实验研究时只能对轮胎内部的几个点位进行温度测试,利用实验的手段不能得到轮胎整体的温度场分布情况,只能获得部分区域的温度分布信息。在此之后一些学者利用简化的轮胎模型来进行解析,以便获得轮胎的温度场分布情况,此方法使用的模型过于简化,只能获得半定量或定性的研究结果,不能够将轮胎的实际温度场准确的反应出来。随着最近几年大型商业软件的发展及非线性有限元理论的成熟使得分析轮胎实际温度场的分布情况更加精准。19世纪80年代初有一些科学家使用解耦的方式将轮胎的热力耦合分析分解成热传导分析、损耗计算及变形分析三部分,为早期轮胎温度场分布的有限元分析奠定了基础[1-4]。解耦的基本思路为:在计算能量损耗时,利用弹性本构关系的变形结果加上非线性黏弹性模型对能量的损耗进行详细的计算[3]。而在变形分析中则不对橡胶材料的时间相关性及温度相关性进行考虑,只将黏弹性本构关系替换为弹性本构关系。由于当时计算机速度及有限元理论都处于初级阶段,在进行有限元分析时的网格都比较粗糙,所以不能够得到较精准结果,但是这种求解分析方法在科学界还是得到了认同,并在后续得到了推广应用。有一部分科学家利用了解耦的分析思想,并通过ABAQUS软件建立了轮胎在进行轮毂实验时的胎体温度场分布情况的计算方案,使用实验数据反演练法将轮胎侧面的对流热交换系数进行了分段确定,同时对轮胎稳态温度场在不同运行速度情况下的变化情况也进行了考究。以上的分析工作没有考虑轮胎所承受的载荷以及轮胎的静态气压对温度场的影响,所以其分析的结果还需要进行进一步的论证。
本文利用计算与实验相互验证的方式对轮胎在转鼓试验下的实际滚动状态进行分析,并利用解耦的分析计算方式,根据轮胎静态气压及胎侧温度场的测试结果,进行SF31904C卡车30.00R51轮胎稳态温度场的有限元分析。为了有效验证有限元分析结果的准确性需要同时进行轮胎转鼓实验内部温度场分布测试。本文重点分析轮胎的冷态气压及承载载荷等非轮胎自身因素对轮胎稳态温度场的影响。
1 转鼓下温度场实验结论
1.1 转鼓下温度场测试
在转鼓试验台上面开展轮胎温度场分布试验测试。实施方案见表1。实施方案中的行驶速度是轮胎与轮毂接触边缘处的线速度,轮胎在这里处于被动运行状态。为了确保轮胎在试验中的稳态温度场能够达到稳定的状态,将轮胎在不同工矿环境中的运行时间设定为2 h。在进行试验的过程中采用红外热成像仪对轮胎的胎侧温度进行监测记录。如图1所示,将红外热成像仪放置在轮毂试验机的一旁,并将镜头对准需要测量温度的轮胎侧面。同时,在轮胎的内部放置无线胎压传感器,对轮胎内部气压的变化情况进行监测记录。
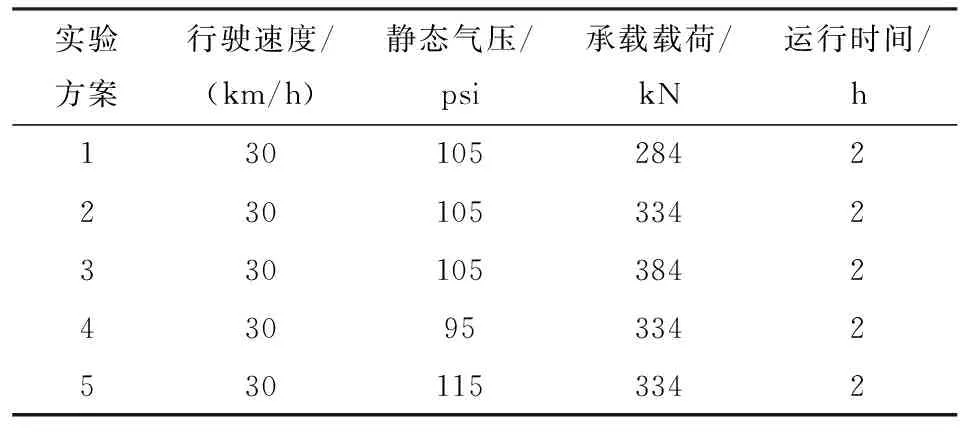
表1 不同环境下轮胎温度场测试实验方案
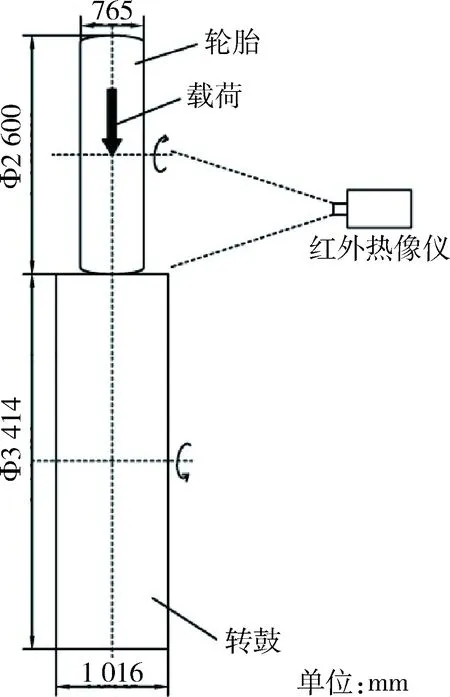
图1 轮胎转鼓试验原理图
1.2 轮胎温度场测试实验结论
轮胎在工作环境为实验方案1的情况下胎侧温度随时间变化在轮胎径向(设定轮胎圆心为坐标原点)方向变化情况如图2所示。由图2可以看出,当轮胎行驶一段时间以后,轮胎的侧面温度场的分布只有很小的上下跳动,因此能够认为此时轮胎侧面的温度场分布已经达到了稳定的状态。同时,在测试结果中体现出了当径向坐标比1.25 m大的时候,轮胎侧面的温度会呈现较明显的下降趋势。其下降的主要原因是胎面位置与散热性能较好的转鼓进行接触,带走了轮胎表面的部分热量,同时由于轮胎在周围空气对流的作用下散发出一部分热量,进而导致其表面温度及附近区域温度急剧下降。在实验中的其他几个实验方案中轮胎侧面的温度场分布情况与实验方案1的情况相似。
在轮胎静态气压相同的前提下,轮胎在承载不同载荷时胎侧温度场变化情况见图3。在轮胎承载相同载荷的前提下,轮胎在不同静态气压情况下的胎侧稳态温度场的变化情况见图4。由图3与图4可以得出:轮胎的承载载荷增加时轮胎的胎侧稳态温度上升;轮胎的静态气压升高时轮胎胎侧的温度则下降。造成此现象的主要原因:当承载载荷固定时,轮胎气压升高,其运行变形降低,能量损耗较少,温度相应降低;在静态气压不变的情况下,随着载荷的增加,轮胎运行时变形量增大,轮胎消耗的能量升高,进而导致轮胎的温度升高。
胎腔内部气体的稳态温度变化情况需要通过间接的方式测算得出。胎腔内部气体压力在静负载试验中的变化情况见图5。从图5可知,胎腔内部气体压力的变化几乎不受轮胎承载载荷大小的影响,在进行静负载实验时胎腔内部的空气温度几乎是不发生变化的,通过理想气体状态方程能够知道轮胎所承载的载荷对胎腔内部气体体积的影响非常少。在对轮胎温度与胎内气压进行实测发现,随着温度的升高胎腔内部气压变化没有大于20%,但是在进行有限元计算时发现温度升高对胎腔内部体积的变化不会大于1%,这就说明在进行实验时气压的改变几乎不影响轮胎内腔体积。所以,在本文中不考虑胎腔体积变化的影响,在计算胎腔内气体稳态温度时直接使用理想气体状态方程,见式(1)。

(1)
式中:T0为轮胎的初始温度;P0为轮胎的静态气压;T1为轮胎达到稳态温度时胎腔空气温度;P1为轮胎达到稳态温度时胎腔空气压力。
在工作环境为实验方案1、方案2、方案3时,设定相同的静态压力,胎腔内部空气稳态温度变化情况见图6;在工作环境为实验方案2、方案4、方案5时,设定相同的承载载荷,胎腔内部空气温度与静态气压关系见图7。从图6与图7能够看出,胎腔内部空气稳态温度的变化规律与胎侧稳态温度的变化规律是相同的,其稳态温度的变化都是随着承载载荷的上升而增加,随着静态压力的升高而降低。
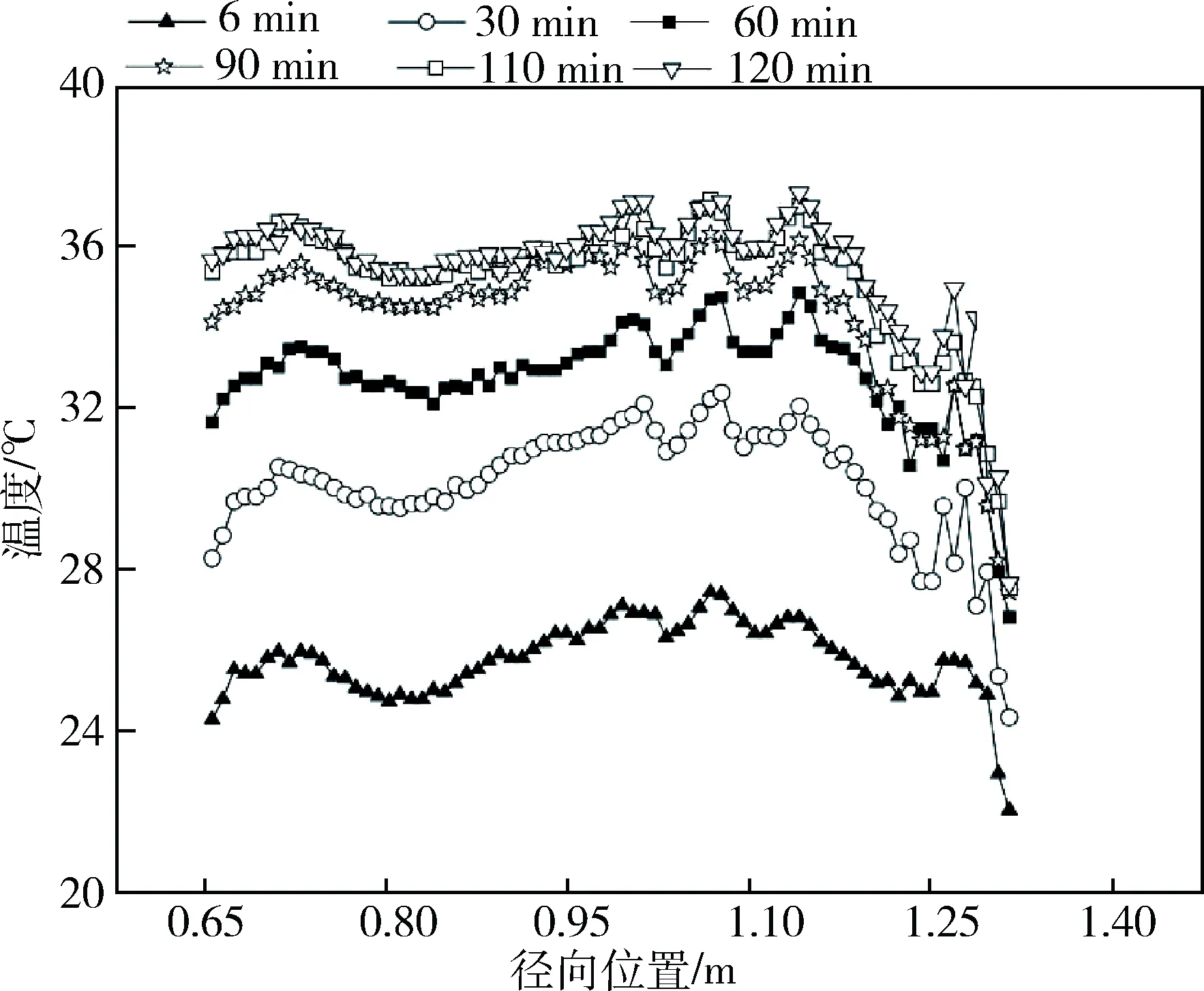
图2 轮胎胎侧温度变化
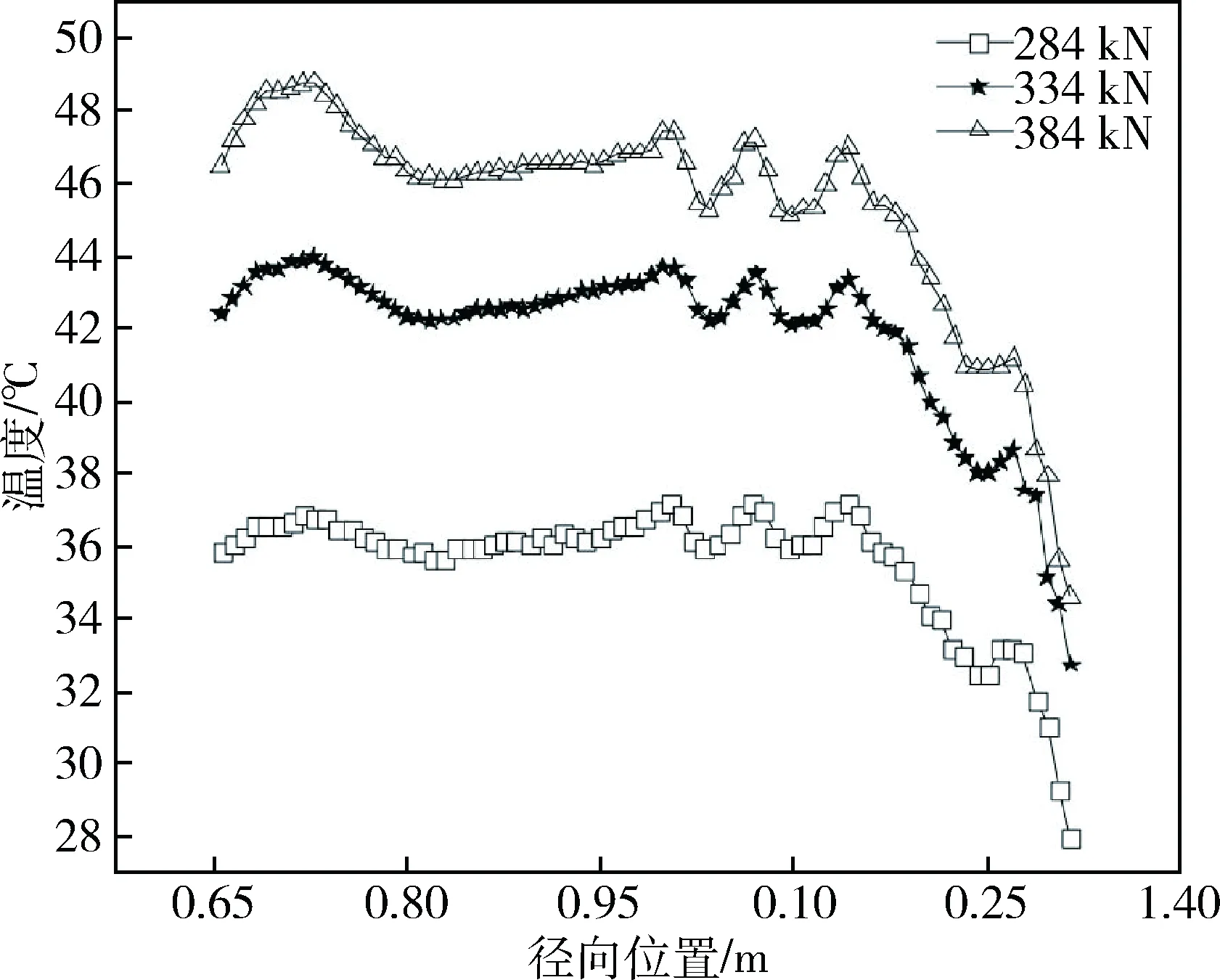
图3 同静态气压下胎侧温度分布
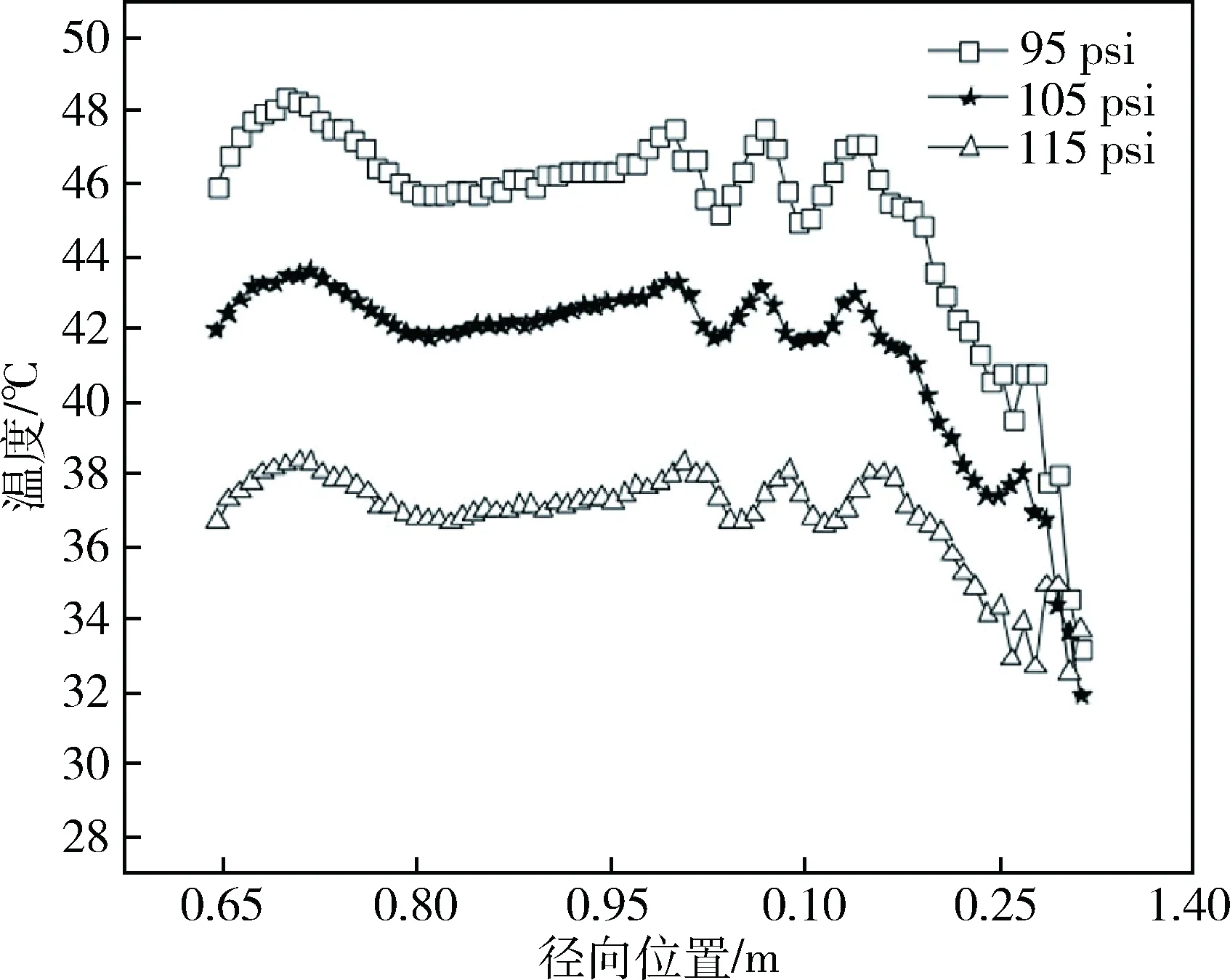
图4 同承载载荷下胎侧稳态温度分布
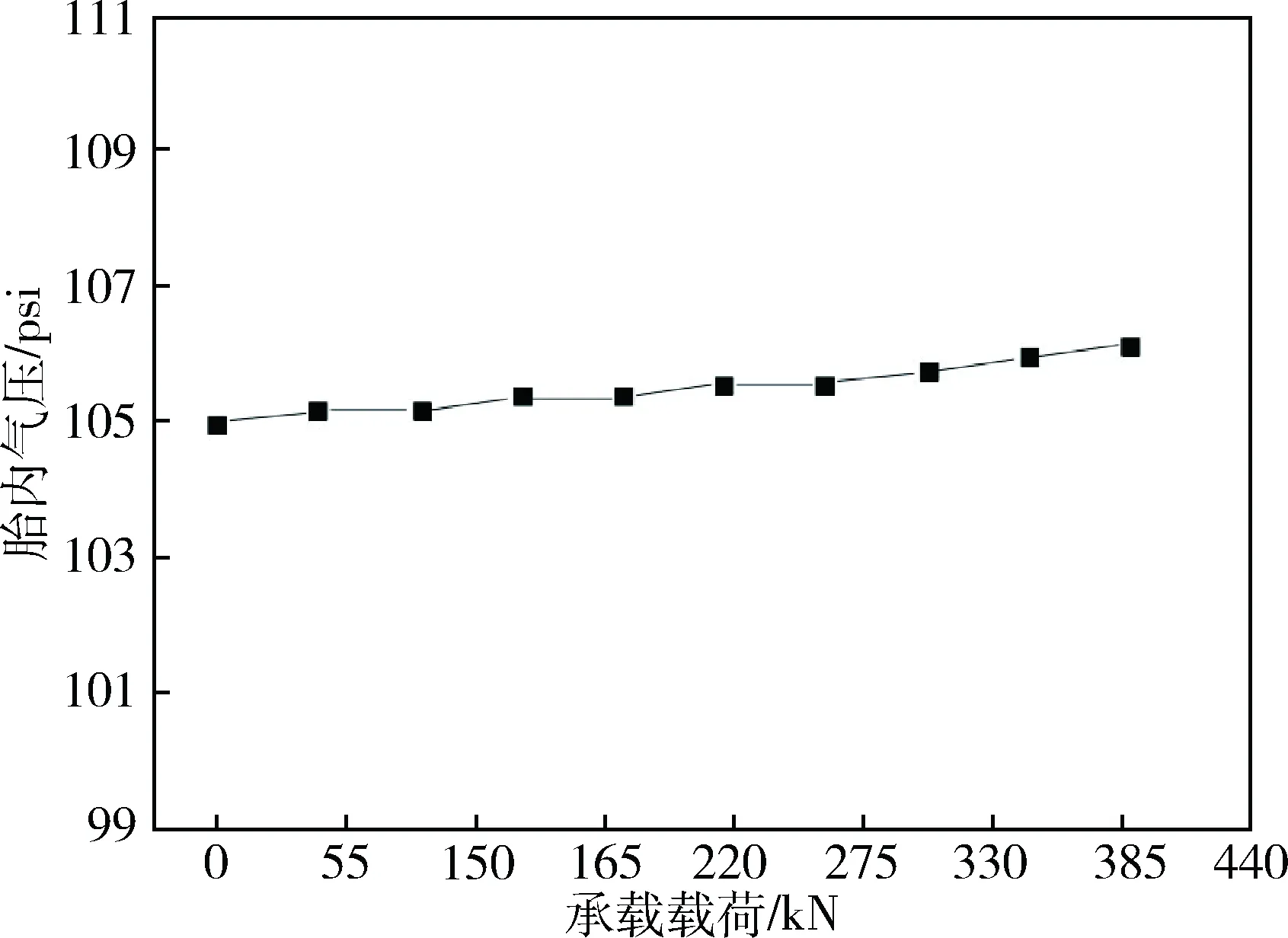
图5 承载载荷与胎内气压关系
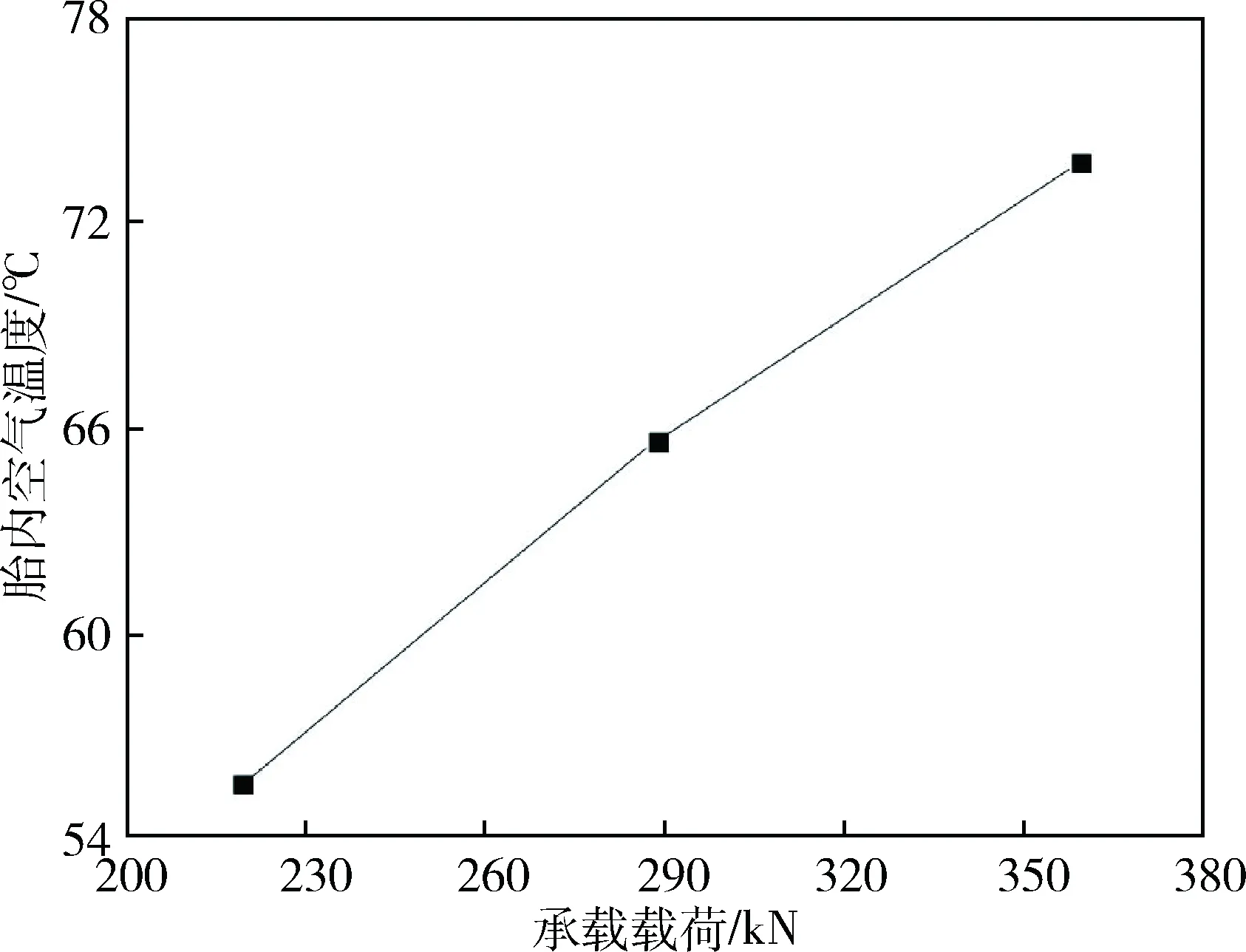
图6 同静态压力下胎内空气温度变化图

图7 相同承载载荷下胎内空气温度变化图
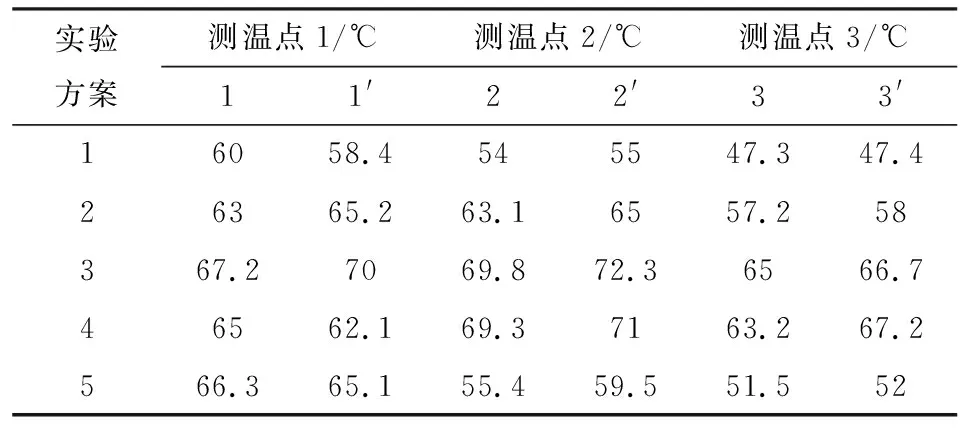
为了有效验证后续有限元的分析结果,需要探测多个实验轮胎的内部稳态温度。其测温方式为:在进行转鼓实验前,在轮胎的胎冠、胎肩等部位打多个小深孔进行内部温度测量,本次试验一共打了6个测温点,测温点分布情况如图8所示,在0°与180°两个轮胎横截面上分别打3个测温点(图8中1(1′)、2(2′)、3(3′));在轮胎行驶2 h后立即将热电偶探头插入实验前打好的小深孔内进行孔低温度测量。由于测量迅速,且小孔的直径很小,可以认为此过程不出现能量损失,假定所测温度为此时轮胎内腔的稳态温度。各位置测得的轮胎内部稳态温度见表2。从表2能够看出,在两个横截面上对应位置点所测得的稳态温度存在差异,但是其差异情况能够接受。此外,在实验方案1、方案2、方案3的工作环境下,测点的温度变化受载荷的影响较大;在实验方案2、方案4、方案5的工作环境下,2#与3#测点的温度随静态气压的升高而下降,但是1#测温点受静态气压的影响则比较小。
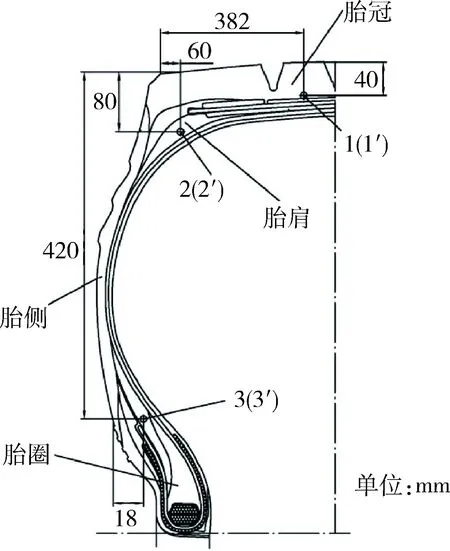
图8 轮胎测温点示意图
表2 胎内测温点温度表
实验方案测温点1/℃测温点2/℃测温点3/℃11'22'33'16058.4545547.347.426365.263.16557.258367.27069.872.36566.746562.169.37163.267.2566.365.155.459.551.552
2 实验条件下轮胎温度场的有限元分析
2.1 有限元分析总体思路
本文对轮胎温度场进行有限元分析的总体思路见图9。在视图中的热传导分析及变形分析都使用ABAQUS有限元软件进行,利用笔者编写的程序进行能量损耗计算,通过计算获取的能量损耗设定为热传导分析的内部热源。
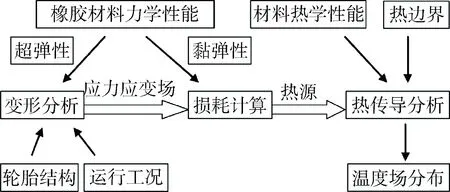
图9 轮胎温度场有限元分析总体思路图
2.2 材料变形计算
依据解耦的理念,在进行变形模块分析中不需要考虑材料参数的时间相关性及温度相关性,使用超弹性的YEOH本构模型作为计算橡胶材料的计算模型。在这里假设橡胶材料是不能被压缩的,所以YEOH形式的应变能函数见式(2)[5]。
U=C10(I1-3)+C20(I1-3)2+C30(I1-3)3
(2)
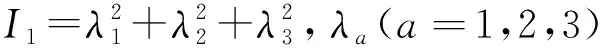
为了减少计算时间以及降低三维建模的难度,在这里对轮胎的一些详细部分不进行分析建模(如标志线、防擦线等),对轮胎的横向花纹也不进行考虑,只对轮胎的纵向花纹造成的影响进行分析。本文认为轮胎的几何形状是轴对称图形,所以对轮胎进行有限元建模,并通过此模型来进行轮胎充气过程及装配过程的分析。进行轮胎稳态滚动及加载过程的分析,需要将此轴对称模型使用ABAQUS软件自带的Symmetric Modle Generation功能直接生成轮胎的3D模型。在这里选用8节点的实体单元C3D8H作为3D模型中的不可压缩橡胶材料,选用4节点的实体单元CGAX4H作为轴对称模型的不可压缩橡胶材料。使用REBAR单元来对轮胎的钢丝圈、胎体层帘线等骨架材料进行定义;定义转鼓以及轮辋材料为刚体。在进行模拟计算时,在轮辋的参考点上加载一个垂直地面的集中,并将转鼓模拟刚体固定;通过加载均布压力在胎体的内表面来模拟胎内气压。
2.3 轮胎在转鼓试验中的滚动状态验证
有的科学家在进行转鼓实验时,认为轮胎是处于自由滚动状态的,即转鼓与轮胎之间是没有相对运动。在这里使用实验与计算相结合的方式来验证转鼓试验中的滚动状态。即通过有限元分析获得转股实验中各种运行环境里轮胎转动的角速度,同时利用转速表分别测得各种运行环境中轮胎转动的角速度。按照转鼓的表面粗糙程度以及其材料,在模拟计算中将转鼓与轮胎间的动摩擦因数设定为0.5,如果轮胎与转鼓间无切向摩擦力则认为此时轮胎是自由滚动的。在进行实验时,将转鼓转动的角速度设定为4.88 rad/s(转鼓边缘线速度为30 km/h),记录不同运行环境下有限元计算得到的角速度与实际测量的角速度,记录见表3。在表3中对比数据发现,计算与实测的数据相差不大于2%,所以能够认为轮胎在仿真计算中是自由滚动的。所以在本文中,分析轮胎稳态温度场时也设定轮胎是自由滚动的。
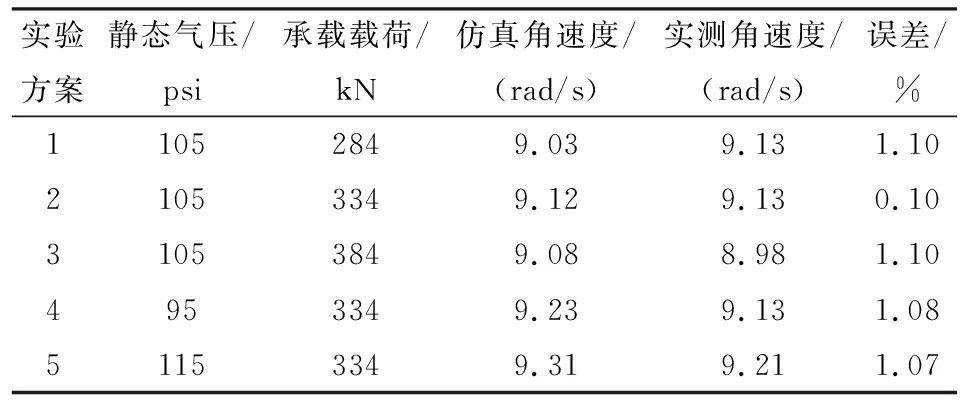
表3 轮胎计算与实测角速度对比表
2.4 损耗能量分析
在轮胎材料的变形分析过程中,将轴对称模型绕中心轴旋转直接生成轮胎的3D模型,这里的3D模型称为一个单元环,轴对称模型称为截面单元,每个截面单元都能够生成单元环。在轮胎稳态温度场分析时轮胎滚动一周的截面单元的应力-应变加卸载过程用每一个单元环沿轮胎周向分布的应力-应变场来代替。再通过傅立叶级数将轮胎稳态滚动中的非谐变等效应力(应变)循环分解成谐波的叠加,见式(3)和式(4)。
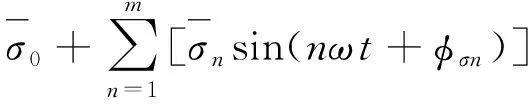
(3)
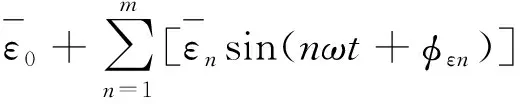
(4)

(5)
式中:δ为黏弹性材料损耗角;ε0为应变幅值;σ0为应力幅值。
频率在5 Hz到几百赫兹时橡胶材料的损耗角变化很小,因此在进行计算时对损耗角的频率相关性进行考虑。所以可以通过试验获得的损耗角及傅立叶分解出来的应力-应变幅值进行能量损耗的计算。整理式(3)~(5)得到式(6)。
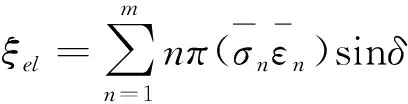
(6)

2.5 稳态热传导有限元分析
进行热传导分析时认为轮胎处于稳态滚动状态,且是一个标准轴对称结构,轮胎各截面分布相同的温度,所以能够将有限元模型建立成为轴对称模型来进行热传导分析,在这里采用与变形分析中一样的网格[5]。对轮胎进行稳态温度场分析是存在内在热源的热传导问题分析[5]。将其离散成网格,则单元的热生成率见式(7)。
ξel=ξel/T
(7)
式中:ξel为热生成率,即单位时间内某个轮胎截面上一个单元所损耗的能量;T为轮胎滚动一周所需时间。
在这里应用ABAQUS软件内的HETVAL对其内部热源进行定义。将轮辋接触面、轮胎内腔表面、轮胎外表面定义为轮胎结构的热传导边界,其示意图如图10所示。将试验中热成像仪收集到的数据直接离散到胎侧边界有限元网格的每个节点上去,当作温度的边界。轮胎内腔的环境温度是内腔气压计算出来的内腔气体稳态温度。剩余的边界则用作对流边界。
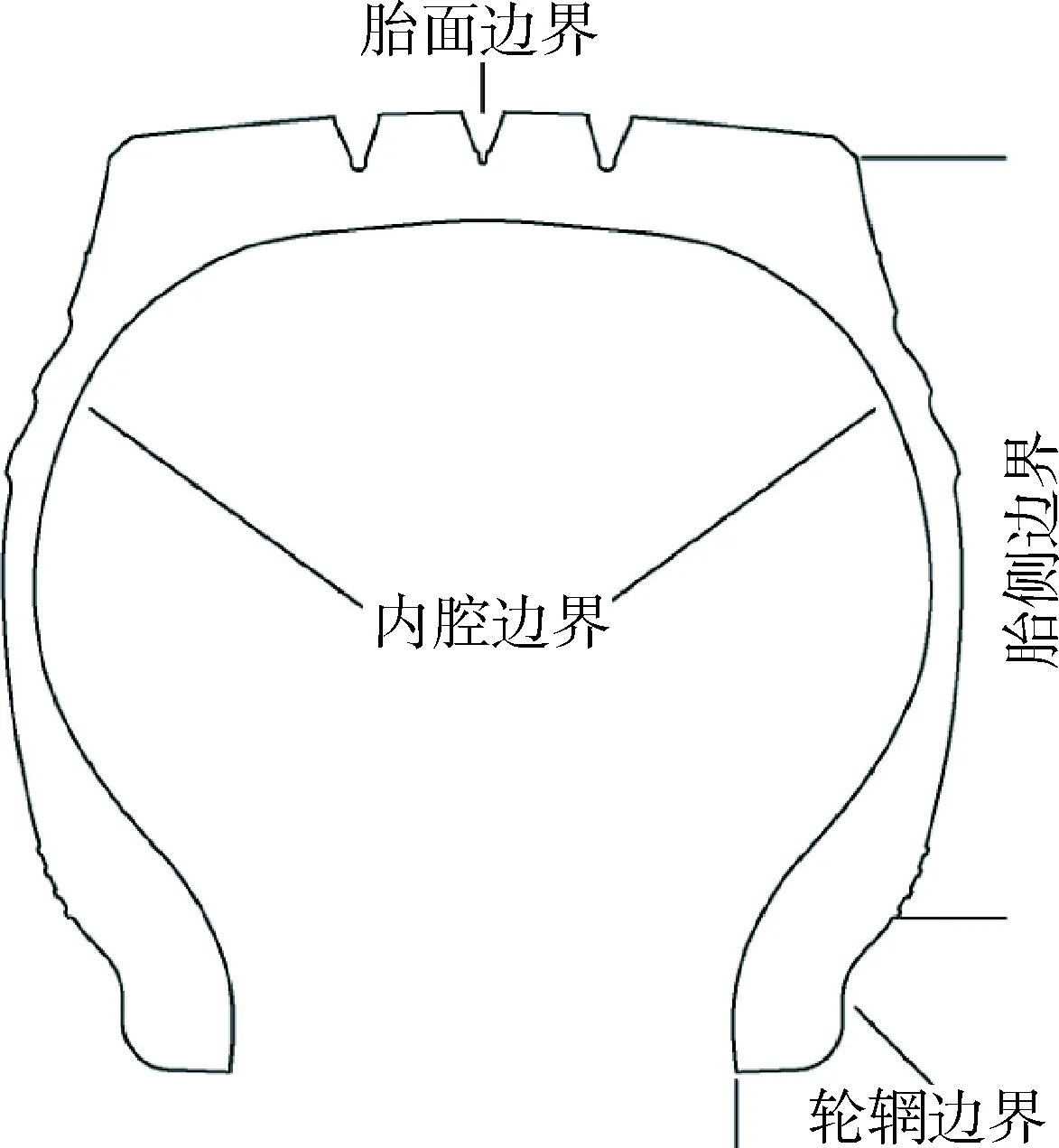
图10 轮胎热传导边界
2.6 温度场的分布结论
本文对5种不同运行环境下的轮胎稳态温度场进行了分析[6]。第一个运行环境中的稳态温度场分布情况见图11。从图11中可以看出轮胎高温的集中区域,其主要是由于橡胶材料的厚度影响热量的散失,导致轮胎胎冠以及胎肩的热量不断积聚稳态温度要比轮胎其他部位高[7]。轮胎内部的6个测温点稳态温度情况见图12,在不同承载载荷情况下内部测温点的稳态温度变化规律如图12(a)~(c)所示,在不同静态压力情况下内部测温点温度变化规律如图12(d)~(f)所示。能够看出,实测的温度分布情况与有限元的分析结果相一致,所以这种分析方式具有较高的准确性[8]。在图12中能够看出:测温点的温度随着承载载荷的增加呈升高的状态;测温点温度随着静态气压的增加而呈降低的状态。造成此现象的主要原因:当承载载荷固定时,轮胎气压
升高其运行变形降低,能量损耗较少,温度相应降低;在静态气压不变的情况下,随着载荷的增加,轮胎运行时变形量增大,轮胎消耗的能量升高,进而导致轮胎的温度升高[9]。
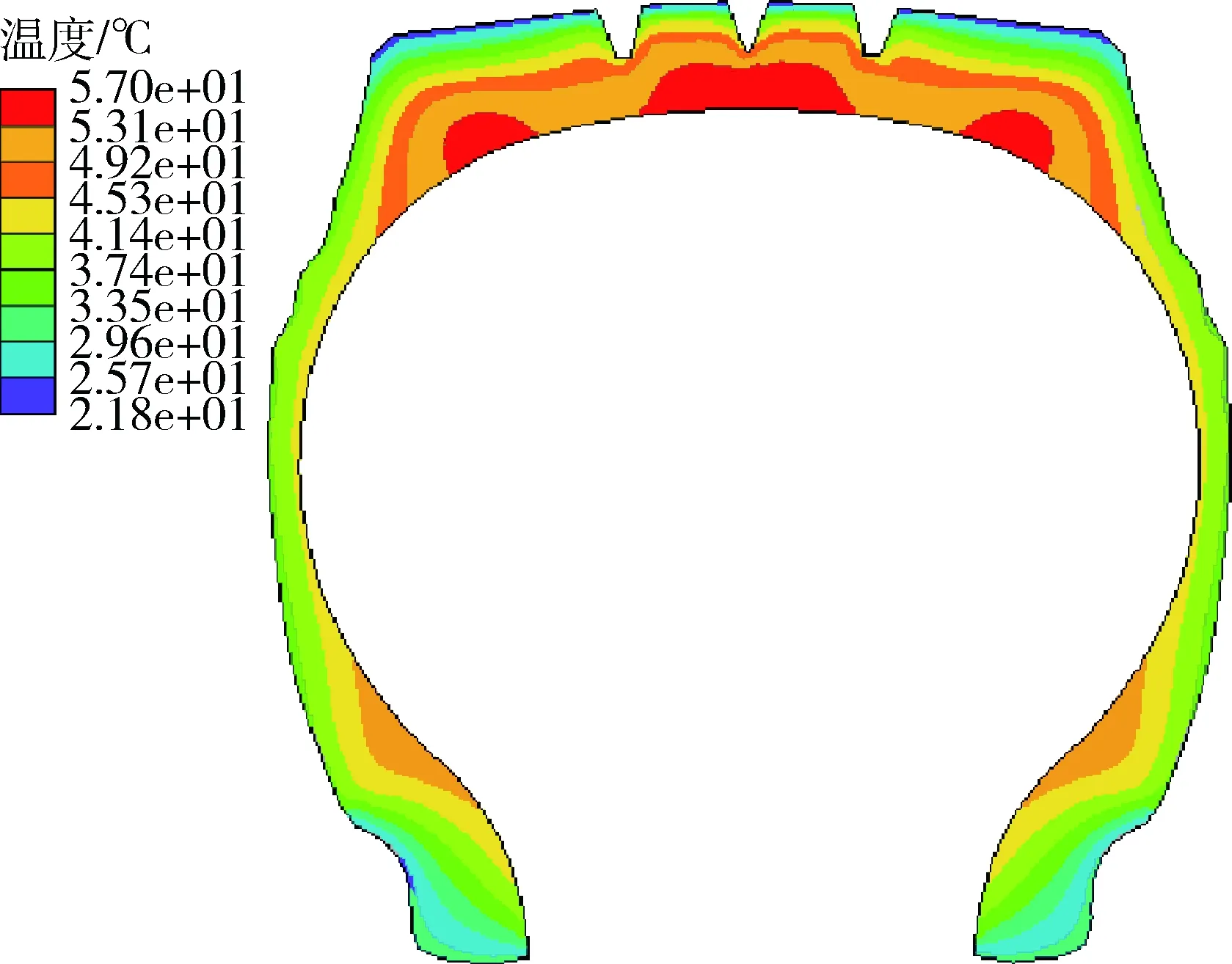
图11 运行环境1中轮胎温度场
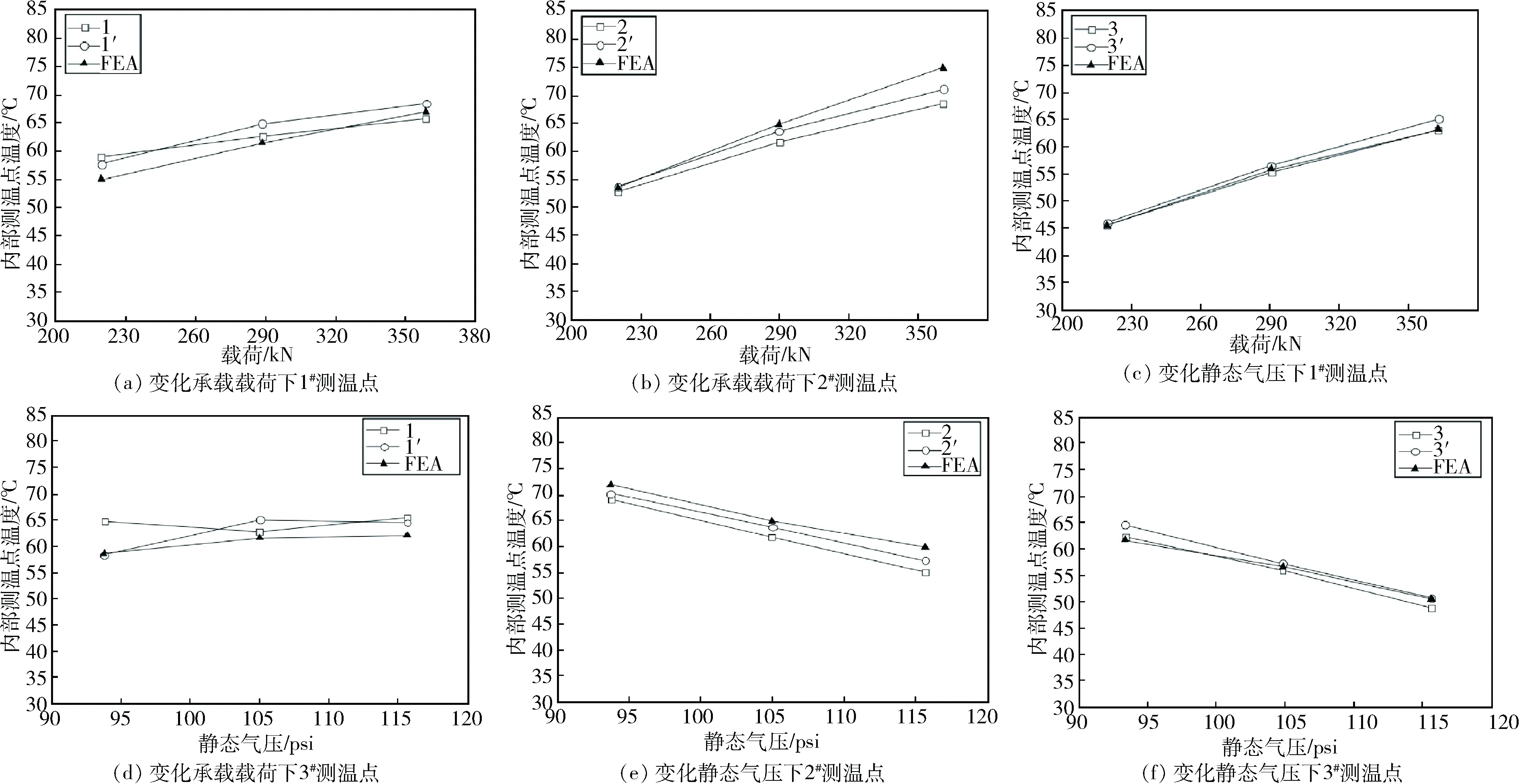
图12 不同条件下轮胎测温点稳态温度变化
3 结 论
本文测试了轮胎在转鼓实验下的稳态温度,同时对胎侧的稳态温度分布、内部测温点的稳态温度以及轮胎内腔稳态气压等情况进行了测量。并使用计算与实验共同进行的方式对轮胎在转鼓试验中的自由滚动无滑移状态进行了对比验证。
通过解耦分析的思路,使用ABAQUS软件对轮胎在转鼓实验中的稳态温度场进行了有限元仿真分析。分析结果表明其数据与实测的数据在变化规律等方面基本一致,说明此方法可用于轮胎稳态温度场分析。本文还重点对轮胎静态气压以及承载载荷等一些外界因素对温度场变化的影响。得出结论:轮胎的稳态温度随着承载载荷的增加呈升高的趋势;随着静态气压的增加而呈降低的趋势;而胎冠区域温度场变化几乎不受静态气压影响。

