基于等时球模型处理时间序列的矢量差分方法
王振齐
(中国政法大学 商学院, 北京 100088)
0 引言
描述时间序列的一类随机模型是Walker[1]提出的自回归移动平均过程(ARMA).假设序列的概率统计特性不随时间改变, 即变化都在固定的均值水平,变动具有相同的方差,ARMA模型较好地刻画了平稳时间序列自相关的演变规律.在很多领域得到了广泛的应用.然而,在工业,商业等领域时间序列不具备固定的均值水平.比如在经济领域,指标由于受到多种非线性因素的作用,呈现波动的不平稳特性.Holt[2]和Winters[3]分别针对存在一定增长趋势的非平稳时间序列、季节性非平稳序列建立指数加权移动模型(EVMA),较好地刻画了这两类特殊时间序列的变化规律.更一般的是易丹辉的著作中Box和Jenkins[4]提出的齐次非平稳模型(ARIMA),采用直接差分的方法将时间序列平稳化,差分后的序列满足了ARMA过程的建模要求.
随着研究的不断深入,文献[5]中的Granger及Hosking,Waxman,Tsay和Ooms等[6-9]在不同领域的研究发现ARIMA过程采用的直接差分容易造成过度差分.最具代表性的是文献[5]中的Granger和Hosking[6],分别独立提出的分数阶差分模型(ARFIMA),对非平稳时间序列进行处理得到了较好的效果.应用研究的经典之作是Ooms等[9]对美国、英国通货膨胀序列进行建模并预测,预测精度相当满意.林雨等[10]基于ARFIMA模型对黄金收益序列进行预测, 实证结果较好.Reisen等[11]通过蒙特卡洛模拟证明5步之内ARFIMA模型的预测能力优于ARMA模型.伍德里奇[12]总结以往的ARFIMA研究,发现大多数统计学家认为,一阶自相关系数大于0.9,就需要进行分数阶差分处理.和直接差分相比,分数阶差分的特点是适当的调整了差分的幅度.
近年来,不少国内学者在差分优化上做了一些尝试.吴亮红等[13]构建了一种自适应权重的差分进化算法.李牧东等[14]提出了基于最优高斯随机游走和个体筛选策略的差分进化算法.戈剑武等[15]提出了一种改进的自适应差分进化算法. 李亚楠等[16]建立了一种基于模拟退火的参数自适应差分演化算法.本文借鉴张昴等[17]提出的矢量差分的方法.一方面改善矢量差分的加法结构以提高差分幅度从而获得更高的预测精度,另一方面用三维空间等时球为框架以解读时间序列的随机特性和自回归特性.
首先以经典力学中的矢量分析法为依托, 用不同大小和方向的作用力对应经济指标受到的多因素.对经济指标进行矢量化处理,在空间直角坐标系中进行正交化分解,用矢量的减法法则处理不平稳数据[18].结合质点沿球中弦下滑的等时性,创建基于等时球中矢量弦的差分方法,并与ARMA过程相结合,建立ARPMA模型.用统计学理论论证了矢量差分法既能较好地刻画相邻两个时点样本的相关程度,又避免了过度差分.最后,将该方法应用于CPI的预测研究,结果表明有着自适应能力的矢量差分法与直接差分法相比,预测精度更高,证明了矢量差分法对非平稳时间序列处理的有效性.
1 基于等时球中矢量弦的差分法原理
1.1 经济指标的矢量特性
多种非线性因素综合作用于经济系统造成了经济指标的不平稳特性,用经典力学理论来阐述经济系统受到的多因素:一个方向上的力对应一种作用因素,一个经济学指标的实现受到了多种大小和不同方向力的作用[18].这是对经济系统非线性根源、经济指标序列非平稳性波动的力学解读.经济指标在这些因素的作用下,其实现路径是曲折的、不规范路径.物理上,有时质点的运动过程也是不规则的,运动轨迹是曲线形式的.在研究质点运动位移时只要知道质点的初始位置.经典力学理论指出位移的大小和方向只和初始位置有关,和其运动路径、运动过程无关,这就是位移的矢量特性,如图1所示.

图1 曲折的路径和规则的位移
在研究经济指标大小变动时,可以借鉴位移的矢量分析特点.把各期经济指标从同一点出发以其大小为长度,按照一定规则画在矢量空间中.此时经济指标有大小和方向两个要素,在矢量空间中有三个维度,这样能更好地反映经济指标大小的不确定性和方向的复杂性[18].物理学中,力的分解、合成运算是按照矢量法则进行的.那么受多种因素作用的经济指标也应该用矢量法则进行分析.下面先介绍非平稳经济指标的矢量差分法则.然后探究经济指标等间隔采集特性的力学机制,用质点沿球中弦下滑的等时性对其进行刻画,进而用解析几何的方法对球中矢量弦进行差分处理.
1.2 矢量化经济指标的差分法则


图2 矢量差分法则

1.3 质点沿球中弦下滑的等时性和经济指标等间隔采集特性的对应
如图3所示,质点从球面上任意一点P沿直线下滑到球的最低点O所用的时间相等.此即质点沿球中弦下滑的等时性.运用牛顿运动定律和运动学位移公式很容易给出证明.


图3 质点沿球中弦下滑的等时性
2 矢量差分的数值计算及其统计特性
为了坐标系中计算方便,也为了消除指标数量级以便进行三角函数计算,在不改变数据规律的条件下,采用
P=λ|OP|/|OP|max
(1)
式(1)中:0<λ<1.
把原始指标数据映射到[0,λ]区间内.在等时球模型中λ的值即为指标数据中的最大值.下面从动力学最降速原理给出指标数据中最大值的产生条件.
2.1 数据最大值在动力学最降速特性下产生

图4 45 °倾角斜槽的最降速特性

(2)
把原始指标数据标准化后用解析几何理论对其做差分计算.
2.2 对球上弦进行矢量差分计算的解析几何方法
物理上,对矢量做数值计算的方法是解析几何法.取球的直径为1,矢量指标的仰角(与水平面的夹角)为θ,矢量指标OP在水平面投影的方向角(逆时针,与x轴正方向的夹角)为ω,如图5所示.

图5 对矢量进行数值计算的解析几何法
对经过P点和最低点O的大圆OPO′做分析.根据弦切角定理易得出圆周角∠OPO′等于弦切角θ.在直角三角形OO′P,易得|OP|为sinθ.基于P点的任意性,得出在直径为1的圆中任意圆周角θ对应的弦长为sinθ.此时OP在z轴方向的正投影为sinθsinθ,OP在x轴方向的分量为sinθcosθcosω,y轴方向的分量为sinθcosθsinω.观察x轴分量和y轴分量的数值发现,无论ω为何值,二者矢量和的大小总是为sinθcosθ这表明作用于x,y的不同大小的因素可以组合为数值相等的水平面指标分量xoy,我们称之为矢量指标的随机分量,称z轴分量为趋势分量.若取ω=θ,求得x轴分量sin2θcosθ/2 ,y轴分量sin2θsinθ/2.
对x,y,z三个分量分别进行差分,得到序列{dxn},{dyn},{dzn},进行预测分析,然后还原得到{xfn},{yfn},{zfn},进而根据
(3)
得到预测值序列{pfn}.
2.3 矢量差分的统计特性
分数阶差分能够避免直接差分过度的缺陷,差分特点为(pn-pn-1)d,一般地0.5


图6 自相关系数的自适应调整
观察图6发现,当Δθ较大时ρ就较小.这与连续两期样本点相关性较差时数值相差较大是一致的.因此,矢量差算法的相关系数更符合现实情况.下面选取CPI数据进行实证研究.
3 实证研究
为了证明矢量差分在刻画时间序列非平稳时间序列的有效性,本文选取CPI数据(2000年1月至2018年1月)做分析,共217个数据,选用前205个样本作为训练集,后12个月份样本作为验证集,数据来源于国家统计局.
3.1 CPI序列平稳性检验
首先按照矢量差分的数值计算及其统计特性中的计算方法,对数据进行标准化处理,使用ADF、DFGLS检验对标准化后的序列{Pn}进行平稳性检验,检验结果如表1所示.

表1 归一化后序列的平稳性检验
从表1可以看出,CPI序列未通过ADF、DFGLS检验,此时应当接受序列不平稳的假设,认为序列是非平稳的.
3.2 直接差分处理后建模
直接差分后的序列{dPn}通过ADF检验,可以认为时间序列己经平稳.观察序列自相关函数图像和偏自相关函数图像,选择ARMA(1,2)模型.模型相应输出参数如表2所示.

表2 直接差分建模参数输出
参数估计后,对拟合模型的适应性进行LM检验,发现残差不存在自相关性.对残差序列进行ARCH效应检验,结果表明残差序列不存在波动率聚集现象.因此,该ARMA模型合理.
3.3 矢量差分处理后建模
对标准化后的序列{Pn}在等时球内进行矢量化处理,根据第二部分提出的计算方案,对三个分量序列分别建模处理.矢量差分后的三个分量序列{dxn},{dyn},{dzn} 均通过ADF检验,认为时间序列己经平稳.
序列{dxn}选择ARMA (2,3)模型.模型相应输出参数如表3所示.

表3 序列{dxn}建模参数输出
序列{dyn}选择ARMA (3,3)模型.模型相应输出参数如表4所示.
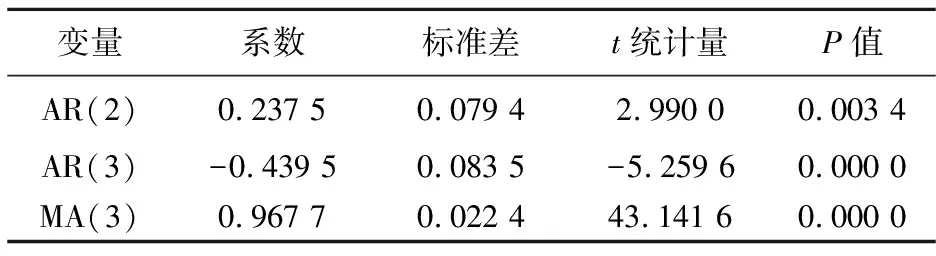
表4 序列{dyn}建模参数输出
序列{dzn}选 择 ARMA(3,3)模型.模型相应输出参数如表5所示.
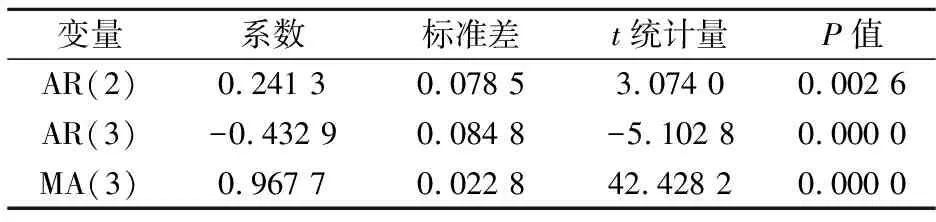
表5 序列{dzn}建模参数输出
对上述三个拟合模型进行LM检验、ARCH效应检验,结果表明模型合理.
3.4 预测和评价
对三个分量序列{dxn},{dyn},{dzn}用静态预测法做检验集的12个月份数据预测,进而还原CPI序列,结果如表6所示.

表6 矢量差分法和直接差分法预测结果
为了更直观地比较矢量差分法、直接差分法的预测效果,釆用绝对百分比误差MAPE、均方误差MSE对预测结果进行评价,结果如表7所示.

表7 矢量差分法和直接差分法误差比较
显然,由表7可以看出,矢量差分法与直接差分法相比,在对CPI序列做预测(2017年2月至2018年1月)时,预测误差更低,绝对误差降低了5%左右,相对误差降低了10%以上,充分显示了矢量差分法在对非平稳数据差分时,因其自相关系数的适应性,避免了过度差分,较好地刻画了序列演变规律.
4 结论
本文采用经典物理学中矢量的分析法为依托,解读时间序列的非平稳性.首先,分别介绍了力学矢量分析的合成、分解原理,矢量数值计算的三角形法则,用矢量减法做差分以处理非平稳序列.接着基于经济指标釆集的等间隔特性,将经济指标在等时球中做矢量化处理.用力学理论给出了最大值和球中矢量弦的对应条件,给出数据标准化公式.进而在空间直角坐标系中对经济指标正交化分解得到三个正交分量序列,对三个序列做差分处理得到平稳时间序列,然后合成矢量差分.考察矢量差分的数值特征发现,矢量差分一方面避免了过度差分,一方面在差分处理时可以做到自适应调整.对CPI序列和三个矢量形式的分序列构建ARMA模型基本一致,进行12个月份的静态预测,发现预测误差更低,绝对误差降低了5%左右,相对误差降低了10%以上,充分论证了矢量差分法在诠释经济数据非平稳特征时的有效性.

