缝洞型碳酸盐岩油藏天然水体倍数估算方法
刘 学, 张占华, 黄 晶, 吴春新, 张 博
(1.中海石油(中国)有限公司 天津分公司, 天津 300452; 2.中海油研究总院, 北京 100028)
0 引言
目前碳酸盐岩油藏探明油气储量约占全球总储量的50%,产量约占全球总产量的65%,开发地位尤为重要[1,2].在众多碳酸盐岩油藏中,裂缝型碳酸盐岩油藏是一种特殊类型的油藏.它是经过多期构造运动与古岩溶共同作用形成的,以岩溶缝洞为主控因素,以缝洞储集体为主的复杂油气藏系统[3,4].储层中流体的主要储集、渗流通道以孔、缝为主,基质的孔隙度以及渗透率都非常小,基本可以忽略不计.由于储层多受风华和剥蚀作用影响,储集空间形态各异,同时非均质性较大[5-11].作为油气田开发中的一项基本工作,能量分析是开发技术政策制订和调整的主要依据.
目前针对缝洞型油藏天然能量评价主要采用以下三种方法:第一种是地质描述法[12,13],它是根据油藏地下资料,以确定圈闭中储藏的流体地下体积来计算水体的大小,该方法通常是在油田开发初期应用,其准确度受地震分辨率的制约.第二种是动态分析法[14-16],该方法主要以油气产量及压力的变化特征为研究对象,应用油气藏工程方法进行分析,将物质平衡理论与油气藏的具体开发地质特征相结合,可以充分的利用油气藏的动态数据,工作量不大但可信度较高.第三种是数值模拟法[17,18],该方法精度高,可是工作量也相对较大.
本文从渗流理论出发,将水侵量转换为油水边界的压力梯度的变化,建立了缝洞型碳酸盐岩储层水侵量的解析数学模型,并对该模型进行求解.通过对比物质平衡方程的水侵量,结合试算法调整无因次半径的数值来确定油藏的天然水体倍数,数值模拟验证具有一定的可靠性,同时还具有简单、快捷的特点,适合类似油藏的矿场应用.
1 水体计算方法
裂缝-孔隙-溶洞三重介质油藏井底压力特征主要分为三个阶段.
第一阶段:假设裂缝与溶洞相联通,溶洞和裂缝系统中的原油流入井筒.基质岩块仍保持原来的状态,其压力Pm保持不变,没有流动.这时井底压力所反映的是溶洞系统和裂缝系统特性.其流动性与均质油藏基本相同,裂缝-溶洞系统压力降落不多,Pf+Pc与Pm差值较小,尚未建立起基质块向裂缝中流动的正常制度.其井底压力特性与均质孔隙储层特性类似.
第二阶段:过度阶段.这时(Pf+rPc)-Pm的差值已有一定程度,能建立起从基质到裂缝-溶洞的流动.基质块空隙中流体压力Pm也逐渐降低.
第三阶段:三重介质阶段.这是原油从基质流入裂缝-溶洞,裂缝-溶洞流入井筒,Pm与(Pf+Pc)同时下降.井底压力变化反映的是孔隙-裂缝整体系统的特性,表现出孔隙-裂缝整体的均质特性.
以边水油藏为例,当供给边界无限大时(re≫rw)可裂缝系统将作为渗流的主要通道,基岩、溶洞主要作为流体交换的介质,假设油井定产量生产,且内外边界压差恒定,可求得其通解为[19]:
(1)
式(1)中:
(2)
(3)
当油水边界的压力梯度发生变化时将产生水侵,因此得出:
(4)
根据公式(4)求出水侵量的计算公式:
(5)
求出水侵量的计算公式为:
(6)
代入无因次表达式化简得[20]:
(7)

(8)
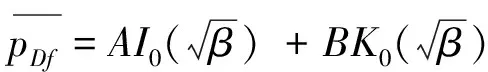
(9)
对(9)式进行Stehfest数值反演
(10)

由式(10)即可求得不同tD对应的无因次水侵量QD的值,在代入式(7),即:
(pi-pwf)QD
(11)
则累积水侵量为:
(12)
根据假设条件已知,发生水侵的主要原因是含水区岩石和流体的弹性膨胀引起的,水侵为非稳态水侵.可以将式(12)简化为:
(13)
(14)
(15)
式(1)~(15)中:m、f、c—基岩、裂缝、溶洞;k—渗透率,μm2;μ—粘度,mPa·s;λ—窜流系数;Cm、Cf、Cc—压缩系数,1/MPa;pwf—井底流动压力,MPa;pi—原始地层压力,MPa;re—供给半径,m;rw—井筒半径,m;pm、pf、pc—压力,MPa;We—一定压力降阶段的累积水侵量,m3;△pk—阶段压力降,MPa;Q(tD)—无因次水侵量;tD—无因次时间.
计算水体的步骤为:
(1)应用物质平衡方程计算累积水侵量,缝洞系统的物质平衡方程为:
(1+m)Cc]Δp
(16)
其中地层水的体积系数(Bw)与水的密度(ρw)可近似等于1,则累积水侵量为:
(17)
(2)根据式(14)、(15)计算无因次时间tD与阶段压力降Δpk.

(4)调整无因次半径rD的数值,使物质平衡法计算的水侵量的与非稳态法计算的水侵量基本相同,利用rD计算水体规模.
(18)
2 实例分析
渤海X油田为一个利用天然能量开发的边水碳酸盐岩油藏,其地质参数和流体参数如表1所示.为了进一步确定油藏的天然能量和后期是否需要转为注水开发等问题,需要确定天然水体的倍数,分别采用解析法和数值模拟法计算了该油田的水体,该油田的历史生产数据如表2所示.

表1 部分地质参数和流体性质参数

表2 渤海X油田历史生产数据
根据非稳态法计算水体,化简物质平衡方程公式(17).由于该区块没有气顶,因此在公式(17)中m=0,Bo≈Boi,Bg≈1.
(19)
根据公式(19)求出累积水侵量为71.99×104m3.
根据公式(15)求出无因次水侵时间,再由公式(14)求出阶段压降,计算结果如表3所示.

表3 非稳态水侵量计算结果
当rD=6.0时,利用公式(13)求出累积水侵量为68.19×104m3.通过计算表明,当rD=6.0时,非稳态水侵量大于物质平衡方法计算的数值,重设rD的值;当rD=7.0时,计算得到非稳态水侵量为77.35×104m3.
根据计算结果采用插值法计算rD=6.66,根据式(18)计算水体倍数为84倍.
渤海X油田数值模拟模型如图1所示.全区地质储量为1 400×104m3左右,全区含水拟合较好(如图2),在此基础上计算得到水体体积为12.12×108m3,水体倍数为86.57倍,基本与本文方法计算的结果一致.但是,数值模拟法需要对油藏的生产动态进行拟合,过程较为复杂,因此本文方法对于该类油田估算水体规模具有一定的优势.

图1 渤海X油田数值模拟网格图
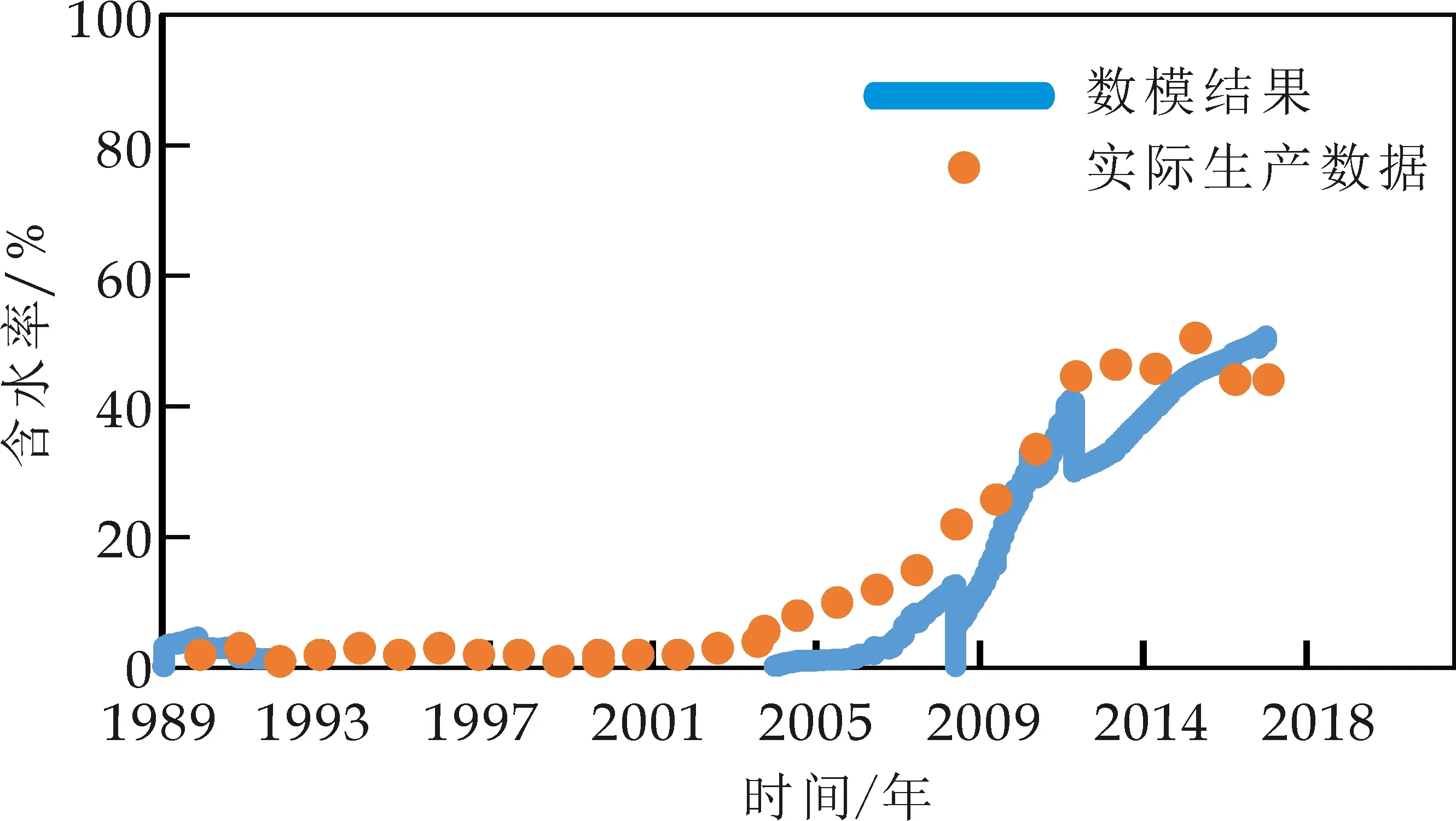
图2 渤海X油田全区含水率拟合图
3 结论
(1)将水侵量转换为油水边界的压力梯度的变化,建立了缝洞型碳酸盐岩储层水侵量的解析数学模型,并通过拉普拉斯变换及Stehfesh数值反演等数学方法得到了该模型的解析解.
(2)结合物质平衡方程,通过求解阶段压力降及无因次时间,得到碳酸盐岩储层的无因次半径,通过试算法调整无因次半径的数值来确定油藏的天然水体倍数,该方法通过数值模拟验证具有一定的可靠性,同时还具有简单、快捷的特点,适合类似油藏的矿场应用.
——以四川盆地云锦向斜茅口组为例

