圆形件卷材排样问题的一种定序定位算法

陆 涛，潘卫平



圆形件卷材排样问题的一种定序定位算法

陆 涛1，潘卫平2

(1. 南宁学院信息工程学院，广西 南宁 530200；2. 广西大学计算机与电子信息学院，广西 南宁 530004)

圆形件卷材排样问题是指将一组不同半径的圆形件互不重叠的排放在宽度指定的卷材上，使得占据的卷材长度最小。针对该问题提出一种定序定位启发式优化算法。设计基于最大穴度的定位算法，对于每个特定排样序列，计算待排样圆形件在当前布局的所有可行放置位置的穴度，选择穴度最高的一个位置放置圆形件；更新当前布局，继续排放剩余圆形件，直到所有圆形件均排放进卷材为止。采用遗传算法对排样序列进行遗传进化得到多种不同的排样方案，选择耗费卷材长度最小的一种排样方案作为最终解。实验结果表明，本文算法排样方案耗费卷材长度较小，且算法计算时间相对合理。

卷材排样问题；圆形件；优化排样；排样算法；定序定位算法

在机械制造领域，经常需要将金属卷材切割成圆形件用来生产各种家用商品，譬如水桶，盘子，杯子等。对圆形件在卷材中的排样方式进行优化，可以减少卷材资源消耗，降低企业生产成本[1-2]。本文研究圆形件卷材排样(circular parts coiled sheet packing，CCSP)问题，该问题在文献[3]的切割与装填布局分类中属于二维开放维度布局问题，在计算理论上属于NP难范畴，具有很高的计算复杂度[4]。

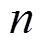
本文针对CCSP问题，提出一种耗时较少的定序定位求解算法。首先构造圆形件的定位算法，计算圆形件在当前布局中各个可行放置位置的穴度，按照穴度最大原则确定圆形件的放置位置；然后采用遗传算法构造多个圆形件排样序列，对于每个排样序列调用上述定位算法确定排样方案，选择卷材使用长度最小的排样方案作为最终解。编程实现本文算法，采用数值实验验证本文算法的有效性。

1 CCSP问题的相关概念

1.1 数学模型

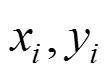
1.2 圆形件放置位置的穴度

如图1所示，在卷材中排入了圆形件1和圆形件2之后，图中虚线给出了圆形件3可能的排放位置。

图1 第3个圆形件在卷材中可能的排放位置示意图

(1)c+1至少与集合S中的2个圆形件相切。

(2)c+1至少与集合S中的1个圆形件相切并且至少与卷材的3条边(左边、上边和下边)中的1条边相切。

(3)c+1至少与卷材的3条边中的2条边相切。

2 排样算法

2.1 定位算法

2.2 定序算法

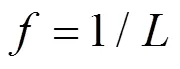
2.2.1 初始种群

初始种群对遗传算法的收敛速度和优化效率具有重要影响。从实际生产经验可知，大小不同的圆形件均匀搭配排放能使布局紧凑，从而提高材料利用率。本节在构造初始种群时借鉴此经验。

2.2.2 遗传算子

2.2.3 终止条件

重复执行第2.2.2节，直到满足预定的进化代数，或计算时间超过规定的最大时间，停止计算，输出适应度最大的个体，得到最优排样方案。

3 数值实验计算

在主频3.2 GHz，内存4 GB的计算机上进行下面两组实验，本文算法进化代数设置为500代，最大计算时间设置为3 600 s。算法排样方案取500代中的最优排样方案；如果算法计算时间超过3 600 s，则取3 600 s内获得的最优排样 方案。

实验1.采用文献[8]的18道例题，将本文算法与文献[8]的3种算法进行比较，分别为开放条带生成算法(open strip generation solution procedure，OSGSP)、改进版的开放条带生成算法(open strip generation solution procedure with a diversification strategy，OSGSPa)和二划分束搜索算法(Beam-Seach and the Binary Interval Search，BSBIS)。求解上述18道例题，本文算法总共耗时10 147.63 s，平均每道例题计算时间为563.76 s，OSGSP算法、OSGSPa算法和BSBIS算法每道例题平均计算时间分别为0.14 s、23.06 s和19 782.58 s。对于18道例题，本文算法排样方案使用卷材平均长度为35.754 8，OSGSP算法、OSGSPa算法和BSBIS算法分别为37.727 3、37.091 9和36.180 8，实验对比结果见表1；本文算法比上述3种算法分别节省5.23%、3.60%和1.78%的卷材长度。因为在定位算法与文献[8]定位算法类似的前提下：①本文定序算法基于遗传算法原理比OSGSP和OSGSPa算法考察了更多个数的圆形件排样序列；②BSBIS算法基于束搜索原理，实质是一种不完全枚举算法，考虑到计算时间和内存空间上的限制，BSBIS算法寻优能力可能劣于本文的定序算法。图2为本文算法求得的例题SY12的排样方案，其卷材宽度为9.5 dm，圆形件的尺寸数据见图3。

表1 SY类例题本文算法与文献算法的计算结果比较

图2 例题SY12的排样方案

图3 例题SY12的50个圆形件的半径数据(dm)

实验2.采用文献[9]的30道例题，将本文算法与文献[9]算法和文献[10]算法进行比较。本文算法求解上述例题，平均每道例题耗时35.62 s，文献[9]和文献[10]未报道例题的具体计算时间，其中文献[10]设置每道例题最大计算时间为30 h。3种算法的实验对比结果见表2，从表中可以看出本文算法比文献[9]和文献[10]分别节省1.58%和0.68%的卷材长度。文献[9]算法是一种贪婪算法，虽然并行化提高了其计算效率，但是未能改变其贪婪性；文献[10]算法基于非线性规划模型，在有限的时间内，算法无法找到最优解。图4为本文算法求得的例题KBG_SPP3的排样方案。

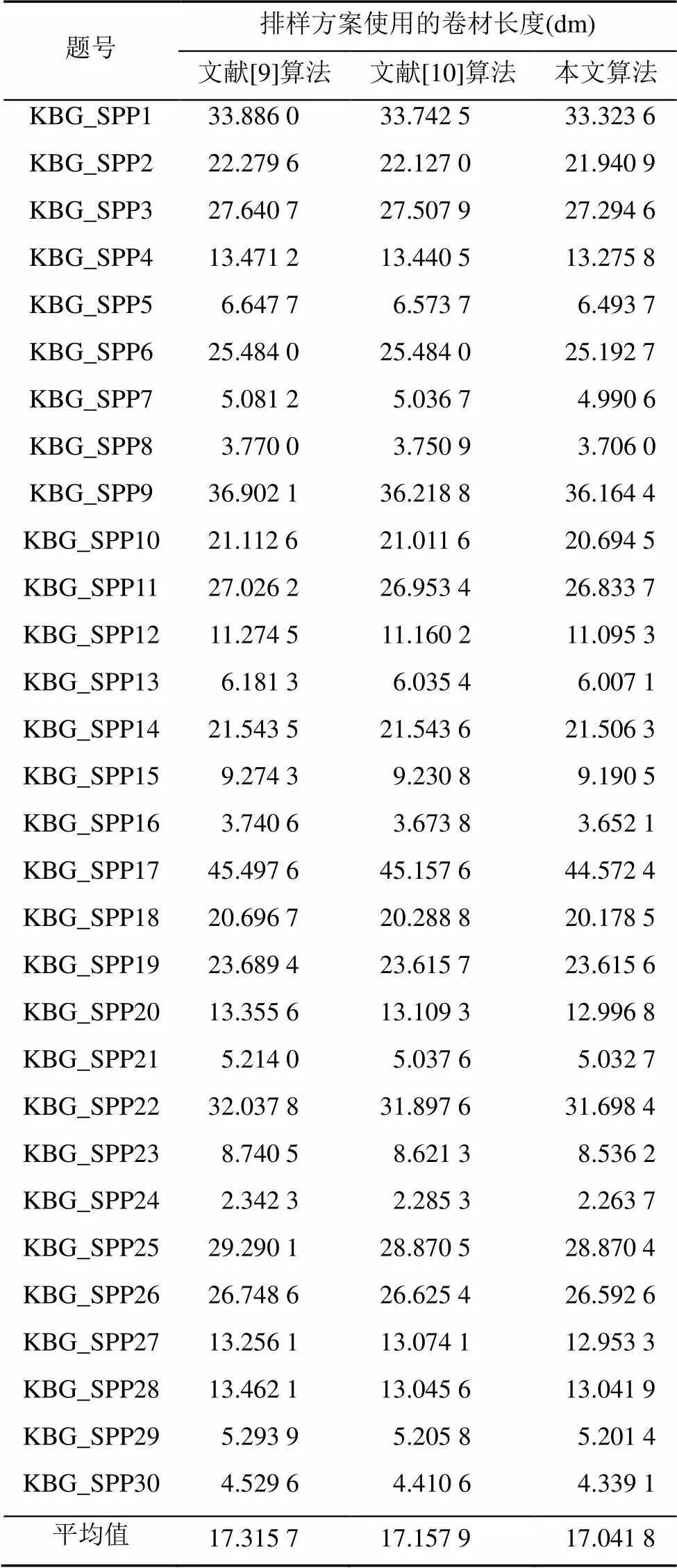
表2 KBG_SPP类例题本文算法与文献算法计算结果比较

图4 例题KBG_SPP3的排样方案

4 结束语

针对圆形件卷材排样问题，构造了一种基于定序定位思想的排样算法。该算法将排样过程分为定序和定位2个阶段，在定序阶段确定圆形件的排放顺序，在定位阶段确定圆形件的具体排放位置。对于一个特定的排样序列，定位算法按照放置位置穴度最大原则确定当前待排圆形件的排放位置。为了扩大解空间的搜索范围，定序阶段采用遗传算法构造了大量不同的排样序列，选择其中最优的一个排样序列作为最终解。从2组实验计算结果，可以看出本文算法具有较高的节材能力和合理的计算时间。

[1] 胡钢, 杨瑞, 潘立武. 基于价值修正的圆片下料顺序启发式算法[J]. 图学学报, 2016, 37(3): 337-341.

[2] 陈燕, 刘咏, 谢琪琦, 等. 基于梯形和平行四边形的圆片剪冲下料算法设计与实现[J]. 图学学报, 2016, 37(5): 661-667.

[3] WÄSCHER G, HAUßNER H, SCHUMANN H. An improved typology of cutting and packing problems [J]. European Journal of Operational Research, 2007, 183(3): 1109-1130.

[4] HUANG W Q, LI Y, AKEB H, et al. Greedy algorithms for packing unequal circles into a rectangular container [J]. Journal of the Operational Research Society, 2005, 56(5): 539-548.

[5] CÔTÉ J F, DELL´AMICO M, LORI M. Combinatorial benders’ cuts for the strip packing problem [J]. Operations Research, 2014, 62(3): 643-661.

[6] 姚怡, 吴金春, 赖朝安. 采用分层搜索填充策略的启发式带排样算法[J]. 武汉大学学报: 工学版, 2014, 47(6): 854-858.

[7] CUI Y P, ZHOU Y W, CUI Y D. Triple-solution approach for the strip packing problem with two-staged patterns [J]. Journal of Combinatorial Optimization, 2017, 34(2): 588-604.

[8] AKEB H, HIFI M. Algorithms for the circular two-dimensional open dimension problem [J]. International Transactions in Operational Research, 2008, 15(6): 685-704.

[9] KUBACH T, BORTFELDT A, GEHRING H. Parallel greedy algorithms for packing unequal circles into a strip or a rectangle [J]. Central European Journal of Operations Research, 2009, 17(4): 461-477.

[10] STOYAN Y, YASKOV G. Packing unequal circles into a strip of minimal length with a jump algorithm [J]. Optimization Letters, 2014, 8(3): 949-970.

[11] 周杰, 周静, 蔡世清, 等. 基于遗传算法的参与式感知激励机制的优化[J]. 科学技术与工程, 2016, 16(17): 230-234.

[12] 刘二辉, 姚锡凡. 基于改进遗传算法的自动导引小车路径规划及其实现平台[J]. 计算机集成制造系统, 2017, 23(3): 465-472.

A Sequential Positioning Algorithm for Problem of Circular Parts Coiled Sheet Packing

LU Tao1, PAN Weiping2

(1. Information Engineering College, Nanning University, Nanning Guangxi 530200, China; 2. Computer and Electronic Information College, Guangxi University, Nanning Guangxi 530004, China)

The problem of circular parts coiled sheet packing means that a set of different radius circular parts are non-overlappingly packed on the coiled sheet with specified width, so that the occupied length of the coiled sheet is minimized. To solve this problem, a sequential positioning heuristic optimization algorithm is proposed. A positioning algorithm is designed based on maximum caving degree. For each particular packing sequence, caving degrees of all feasible placement location of circular parts are calculated, and the location which has the highest caving degree is selected to pack the circular part. The current layout is updated, and the packing of the residual circular parts is continued, according to the above rule until all of circular parts are packed into the coiled sheet. Genetic algorithm is employed to evolve the packing sequence, in order to obtain a great number of different packing schemes, and the packing scheme with the minimum coiled sheet length is chosen as the final solution. The experimental results show that the algorithm scheduling scheme of this paper consumes less coil length, and the calculation time of the algorithm is relatively reasonable.

coiled sheet packing problem; circular parts; packing optimization; packing algorithm; sequential positioning algorithm

TP 391

10.11996/JG.j.2095-302X.2018030562

A

2095-302X(2018)03-0562-05

2017-10-12；

2017-11-15

国家自然科学基金项目(61363026)；广西高校科学技术研究项目(KY2015YB533)

陆 涛(1982-)，男，广西环江人，讲师，硕士。主要研究方向为软件工程、人工智能和大数据。E-mail：ltgx82@163.com

潘卫平(1989-)，男，湖北黄冈人，工程师，硕士，主要研究方向为优化计算。E-mail：gxwp08@163.com