形状可调的Loop细分曲面渐进插值方法
陈甜甜,闫 迪,王 伟,赵 罡
形状可调的Loop细分曲面渐进插值方法
陈甜甜,闫 迪,王 伟,赵 罡
(北京航空航天大学机械工程及自动化学院,北京 100191)
针对Loop细分无法调整形状与不能插值的问题,提出了一种形状可调的Loop细分曲面渐进插值方法。首先给出了一个既能对细分网格顶点统一调整又便于引入权因子实现细分曲面形状可调的等价Loop细分模板。其次,通过渐进迭代调整初始控制网格顶点生成新网格,运用本文的两步Loop细分方法对新网格进行细分,得到插值于初始控制顶点的形状可调的Loop细分曲面。最后,证明了该方法的收敛性,并给出实例验证了该方法的有效性。
Loop细分;形状可调;渐进插值;权因子
细分曲面造型技术由于具有算法简单、容易实现、可以表示任意拓扑结构的物体等优点,已经在几何造型、计算机动画、游戏等领域得到了广泛的应用[1]。细分方法按其极限曲面是否插值于初始控制顶点分为逼近型细分方法与插值型细分方法。经典的逼近型细分方法有Catmull-Clark细分[2]和Loop细分[3],这类细分方法的极限曲面相对初始网格都会有收缩[4]。典型的插值型细分方法有Butterfly细分[5]和Kobbelt细分[6],这类细分方法的极限曲面不存在收缩,但连续性不好,只能达到整体1连续,而且细分曲面也可能会产生一定程度的变形,因此仅仅凭借初始控制网格无法准确预判其极限曲面的形状。
针对插值型细分的上述缺点,人们提出了利用逼近型细分构造插值细分曲面的方法。HOPPE等[7]提出了一种基于Loop细分的插值型细分方法。NASRI[8]通过修改Doo-Sabin细分方法的规则使之具有插值特性。BRUNET[9]改进了Nasri的方法,增加了形状控制特性。HALSTEAD等[10]提出构造线性方程组反求控制顶点,对反求后的控制网格进行细分,得到细分后的极限曲面插值于初始网格控制顶点。但这些方法需求解线性方程组,方程组有可能是病态的。为了避免繁琐的线性方程组求解,CHEN等[11]和CHENG等[12]分别提出了基于Catmull-Clark细分和基于Loop细分的渐进迭代插值方法。这类方法首先对细分曲面的初始控制顶点进行迭代调整,接着采用已有的逼近型细分方法对调整后的初始控制网格进行细分,不仅易于实现,而且具有较好的曲面连续性。为了进一步提高渐进迭代插值细分方法的灵活性,林晓晶和潘日晶[13]提出了一种基于Loop细分的渐进插值方法,该方法通过引入参数修改Loop细分几何规则,增加了形状调整的灵活性。2014年,CHEN和PRAUTZSCH[14]提出了广义三角形中点细分方法(以下简称广义中点细分),该方法给出了一种广义中点细分模板,在细分过程中引入可调权因子,实现细分曲面的形状可调。文献[13]运用经典Loop细分模板,文献[14]运用广义中点细分模板,两者虽然都能实现形状可调,但是细分模板较复杂,实现过程较繁琐。
通过研究Loop细分与广义中点细分之间的联系,本文给出了一种能对细分网格顶点统一调整的等价Loop细分模板,并在此模板的基础上,提出了一种形状可调的Loop细分曲面渐进插值方法。该方法通过渐进迭代调整初始控制顶点的位置,使得相应的细分曲面插值于初始控制网格。同时通过在本文中给出的等价Loop细分模板中引入权因子,从而实现Loop细分曲面形状可调的特性。
1 等价Loop细分模板
1.1 Loop细分
Loop细分方法是一种基于三角形网格的细分模式,其极限曲面是三向四次箱样条曲面的推广,在正则点和奇异点处可分别达到2连续与1连续。在实现过程中,新顶点-顶点和新边点-顶点采用不同的规则进行计算。文献[3]中给出了新顶点与新边点的计算公式。

1.2 等价Loop细分模板
广义中点细分属于1-4三角形面片分裂细分方法,其细分规则为

其中,R为线性细分;A为加权平均。R运算与A运算如图1所示。

广义中点细分在进行运算之后使用式(4)对所有细分网格顶点进行运算,由式(3)和式(4)得到进行一次广义中点细分之后内部-顶点的计算表达式(5)和内部-顶点的计算表达式(6),即

内部-顶点的计算表达式
(5)
内部-顶点的计算表达式


广义中点细分边界-顶点与边界-顶点的处理方式与Loop细分一致,给出广义中点细分的等价细分模板如图3所示。通过对比该等价细分模板和Loop细分模板可以发现:两者在形式上完全一致。

图3 广义中点细分的等价模板
为了保持Loop细分曲面的形状不变,又兼具广义中点细分的细分网格顶点统一调整的优势,本文给出了一个既能对细分网格顶点统一调整又便于引入权因子实现细分曲面形状可调的等价Loop细分模板。
对比Loop细分的几何规则和广义中点细分的等价模板可知,当权因子满足式(7)时,Loop细分的内部-顶点与内部-顶点才可以进行统一调整,即

其中,为相应的内部-顶点的价,化简得


本节通过分析对比广义中点细分的等价细分模板与Loop细分模板之间的联系,给出了-顶点和-顶点统一调整的等价Loop细分模板。总体来说,等价Loop细分模板有以下两方面的意义,一是能够简化Loop细分算法在计算机上的实现过程,二是便于在Loop细分模板中引入权因子,以实现Loop细分曲面形状可调。

图4 Loop细分网格顶点统一调整的等价细分模板
2 两步渐进插值细分方法
Loop细分是一种基于三角形网格的逼近型细分方法,这种方法的细分曲面不能插值于初始网格的控制顶点,相比于初始网格存在一定的收缩,且细分曲面形状不可调整。因此,本文提出了一种形状可调的Loop细分曲面渐进插值方法,该方法既能实现插值,又可以通过改变权因子的大小实现细分曲面形状可调。
2.1 两步Loop细分
两步细分方法是ZHENG和CAI[16]在2006年首次提出的一种细分方法,该方法实现了Catmull-Clark细分方法的形状可调。本文将这种方法应用于Loop细分,结合迭代插值算法实现形状可调的Loop细分渐进插值方法。具体的两步Loop细分实现过程如下:


(2) 对第(1)步得到的新网格运用等价Loop细分模板进行细分,直至得到极限细分曲面。
2.2 两步Loop细分方法的极限点公式

2.3 迭代插值


3 收敛性证明
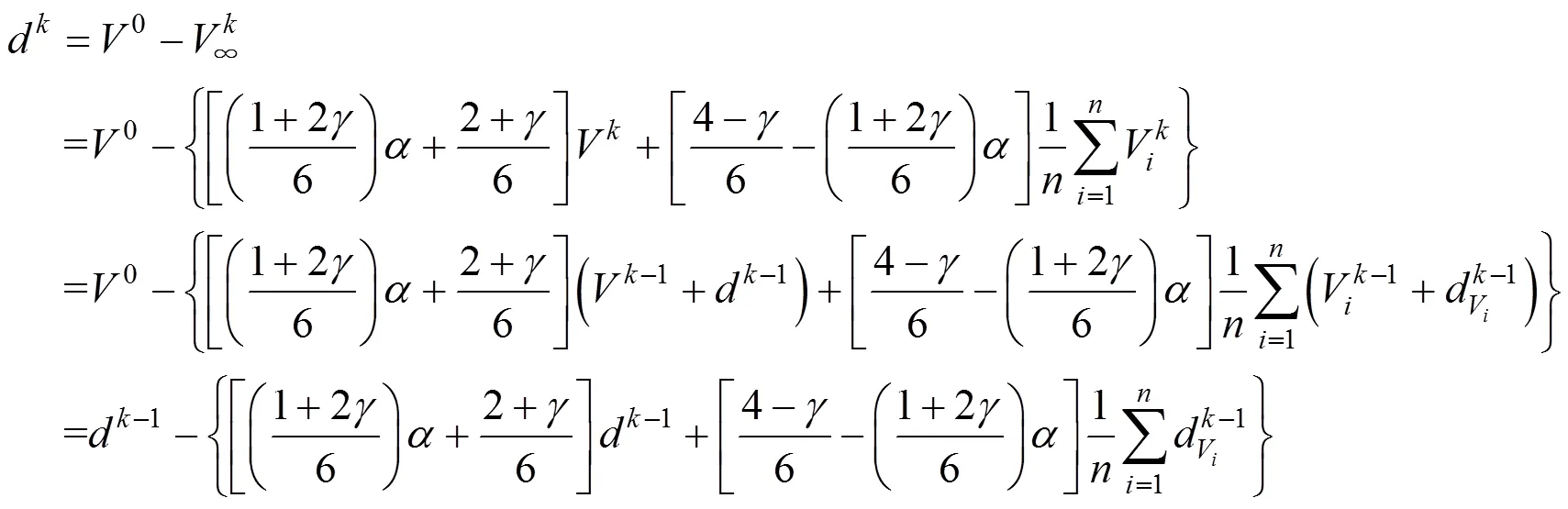
将式(14)以矩阵形式表示


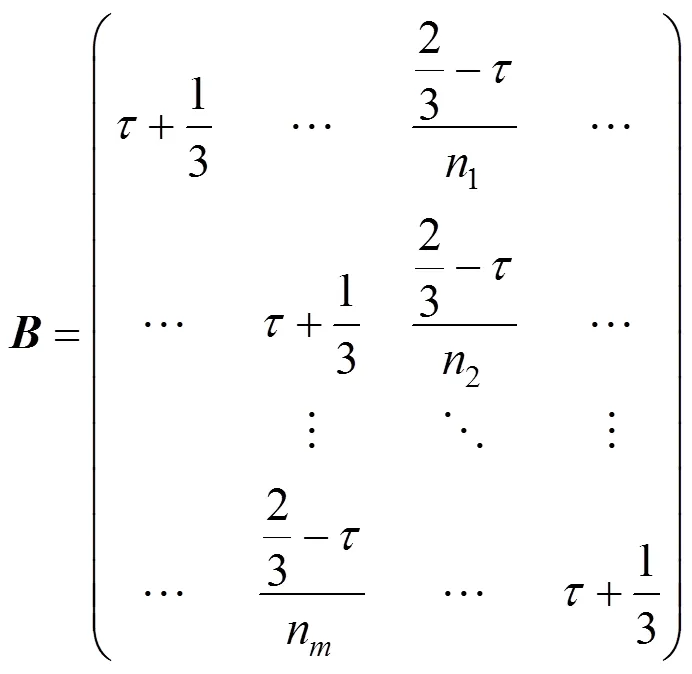
根据矩阵的这些性质,可将其分解为一个对角矩阵和一个对称矩阵,即。其中,对角矩阵为

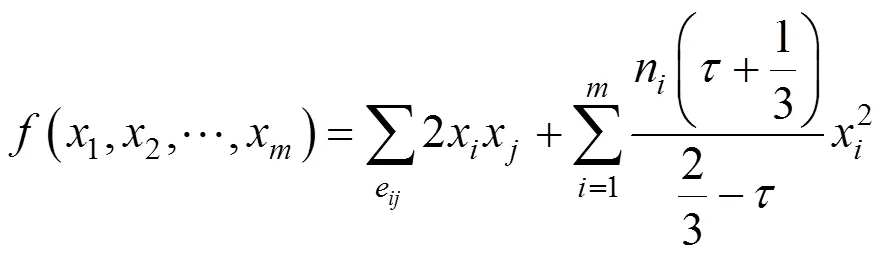

故

引理3. 正定矩阵的特征值是正值。
4 算法实例
所有实验均在配置为Intel(R) Core(TM) i5-6500 CPU @ 3.20 GHz 处理器和8 GB内存的电脑上进行,程序运行环境为Visual Studio 2010。实验均在Knot、Cat、Pig和Bear等4种网格模型的基础上进行。
首先,为了对比传统Loop细分模板与等价Loop细分模板的运行时间,以Loop细分4次为例,对4种网格模型进行了实验,实验数据见表1。从表1中可以看出,随着初始网格顶点数的增加,等价Loop细分模板在实现Loop细分上的优势愈发明显,效率更高。

表1 传统Loop细分方法与等价Loop细分模板的运行时间对比


图 5 不同值所对应的Knot 模型插值曲面

图 6 Loop 细分曲面及不同值所对应的Cat 模型插值曲面

图 7 Loop 细分曲面及不同值所对应的Pig 模型插值曲面

图 8 Loop 细分曲面及不同值所对应的Bear 模型插值曲面
5 结 论

[1] 李桂清. 细分曲面造型及应用[D]. 北京: 中国科学院计算技术研究所, 2001.
[2] CATMULL E, CLARK J. Recursively generated B-spline surfaces on arbitrary topological meshes [J]. Computer Aided Design, 1978, 10(6): 350-355.
[3] LOOP C T. Smooth subdivision surfaces based on triangles [D]. Salt Lake City: Department of Mathematics University of Utah, 1987.
[4] ODER P S, ZORIN D, DEROSE T, et al. Subdivision for modeling and animation [C]//ACM SIGGRAPH 2000 Course Notes. New York: ACM Press, 2000: 65-102.
[5] DYN N, LEVIN D, GREGORY J A. A butterfly subdivision scheme for surface interpolation with tension control [J]. ACM Transaction on Graphics, 1990, 9(2): 160-169.
[6] KOBBELT L. Interpolatory subdivision on open quadrilateral nets with arbitrary topology [J]. Computer Graphics Forum, 1996, 5(3): 409-420.
[7] HOPPE H, DEROSE T, DUCHAMP T, et al. Piecewise smooth surface reconstruction [C]//Conference on Computer Graphics and Interactive Techniques. New York: ACM Press, 1994: 295-302.
[8] NASRI A H. Polyhedral subdivision methods for free-form surfaces [J]. ACM Transaction on Graphics, 1987, 6(1): 29-73.
[9] BRUNET P. Including shape handles in recursive subdivision surfaces [J]. Computer Aided Geometric Design, 1988, 5(1): 41-50.
[10] HALSTEAD M, KASS M, DEROSE T. Efficient, fair interpolation using Catmull-Clark surfaces [C]// Proceedings of the 20th Annual Conference on Computer Graphics and Interactive Techniques. New York: ACM Press, 1993: 35-44.
[11] CHEN Z X, LUO X N, TAN L, et al. Progressive interpolation based on Catmull-Clark subdivision surfaces [J]. Computer Graphics Forum, 2008, 27(7): 1823-1827.
[12] CHENG F H, FAN F T, LAI S H, et al. Loop subdivision surface based progressive interpolation [J]. Journal of Computer Science and Technology, 2009, 24(1): 39-46.
[13] 林晓晶, 潘日晶. 一种基于Loop细分的渐进插值方法[J]. 福建师范大学学报: 自然科学版, 2014(1): 18-24.
[14] CHEN Q, PRAUTZSCH H. General triangular midpoint subdivision [J]. Computer Aided Geometric Design, 2014, 31(7): 475-485.
[15] MA W Y, MA X H, TSO S-K, et al. A direct approach for subdivision surface fitting from a dense triangle mesh [J]. Computer Aided Design, 2004, 36(6): 525-536.
[16] ZHENG J, CAI Y. Interpolation over arbitrary topology meshes using a two-phase subdivision scheme [J]. IEEE Transactions on Visualization and Computer Graphics, 2006, 12(3): 301-310.
A Progressive Interpolation Scheme for Loop Subdivision Surfaces with Shape Adjustment
CHEN Tiantian, YAN Di, WANG Wei, ZHAO Gang
(School of Mechanical Engineering and Automation, Beihang University, Beijing 100191, China)
Aming at the problems that Loop subdivision can’t satisfy the shape adjustment and interpolate the given mesh, a progressive interpolation scheme for Loop subdivision surfaces with shape adjustment is presented. Firstly, an equivalent Loop subdivision mask that can adjust the mesh vertices uniformly and facilitate the introduction of weight to adjust the shape of subdivision surfaces is proposed. Secondly, the new grid is generated by the iterative adjustment of the initial control grid, and using the two-phase Loop subdivision scheme presented in this paper to subdivide the new mesh, the shape-adjustable Loop subdivision surface that interpolate the initial control vertices is obtained. Finally, the convergence of the scheme is proved and some typical examples are illustrated to verify its effectiveness.
Loop subdivision; shape adjustment; progressive interpolation; weight
TP 391
10.11996/JG.j.2095-302X.2018030395
A
2095-302X(2018)03-0395-07
2017-01-14;
2017-05-11
国家自然科学基金项目(51305016,61572056)
陈甜甜(1982–),女,上海人,实验师,博士,硕士生导师。主要研究方向为CAD/CAM、复杂曲线曲面造型。E-mail:chentt@buaa.edu.cn

