反推火箭燃烧产物空间羽流场污染分析

陈思佳，刘　岭，翟　博，邱亚男，胡辉彪

(北京宇航系统工程研究所，北京，100076)

0　引言

卫星与运载火箭之间的分离可通过安装在箭体四周的固体反推火箭(以下简称反推火箭)产生燃气混合物羽流来提供分离能源实现可靠分离[1]。反推火箭燃气从喷管喷出，即由高密度连续介质流逐渐演化为低密度气体自由分子流，从而形成一个反推火箭燃气羽流影响区域，并对卫星产生污染[2]。通常可以采用地面试验和数值模拟仿真分析[3]。地面试验模拟成本高昂，周期长，而且推力大于20 N的发动机的羽流地面试验就比较困难，因为背压很难保持足够低的水平[4]。因此对于大推力发动机的高空羽流模拟，以数值计算为主。程晓丽和王强等人[5]利用Woronowicz等人提出的自由分子单一点源模型推广建立的的非均匀出口条件下的工程分析模型[6]，分析了10 N双组元发动机的羽流流场和污染分布。张建华等人采用Simons方法分析了发动机羽流分布。不过工程方法只适合在方案研制阶段，进入后期设计，还需要更可靠的数值模拟方法。褚洪杰采用CFD和工程方法相结合预测了高空羽流的污染分布，程晓丽等人[9]采用DSMC方法分析了高空羽流。钱中[10]等人也分析了羽流中粒子的分布情况。不过DSMC方法受限计算量太大，应用受到限制。Gatsonis 等人[10]采用CFD/DSMC方法求解了冷工质的高空羽流分析。在本文中，将采用CFD/DSMC方法分析1万牛量级的反推火箭的羽流分布和对卫星污染情况进行数值模拟仿真；对反推火箭安装于火箭的不同位置、不同安装角的燃气喷出物羽流特征进行计算，并对数值计算结果进行比对分析，得到反推火箭不同的安装位置与安装角度所形成燃气喷出物羽流场对卫星污染的影响。

1　反推火箭羽流场计算方法

反推火箭燃气羽流流场始于喷管内部的燃气流动，由于喷管内部气流密度高，能够满足连续流基本假设条件，喷管内部的流动可采用二维轴对称N-S方程或带滑移流边界条件的N-S方程数值计算方法进行模拟计算。在喷管出口附近的流动进入近连续滑移流动，采用带滑移边界条件的N-S方程解算器捕捉喷管内部出口附近的流动信息。气体在流出喷管后急剧膨胀而变得越来越来稀薄，连续介质流假设开始遭到破坏，对于远离喷管出口的羽流区N-S方程已不适用于羽流流动特征的描述,则喷管外羽流流场计算采用DSMC方法。因此，本文反推火箭羽流场数值计算采用N-S/DSMC耦合算法技术解决CFD与DSMC两种方法间的计算过渡问题。

反推火箭燃气从喷管内流动到羽流核心区、近场区到远场区以及卫星载体影响区流动时，气流密度从近场高密度核心区变化为远场高稀薄微小密度的羽流粒子区。仅使用DSMC计算方案无法对密度剧烈变化的燃气流场进行数值。因此，在数值计算时采用区域分解方法，将喷口外适于DSMC方法描述的羽流流场分解为临近喷口的近场核心区、远场羽流区以及贴近火箭、卫星表面的羽流粒子撞击区。

对于临近喷口的高密度羽流近场核心区，使用DSMC方法模拟计算。由于该区域羽流流动毗邻喷管超音速高温、高压燃气流，则近场核心区气流密度大。因此，数值计算网格采用二级笛卡尔直角网格，在计算过程中对网格进行自适应调整，以满足网格长度羽流平均自由程λ的要求，准确地反映流场物理量的变化梯度。

对于羽流核心区的远场羽流区，气流密度急剧下降，背景低压工作环境导致羽流不断快速膨胀，羽流流场从近连续流变化到稀薄过渡流、高稀薄自由分子流。羽流流场进一步变成速度减小的稀薄气体分子流动，需考虑减小DSMC计算出现统计散度过大的问题。对于远场区羽流流场计算在采用DSMC方法的同时，需增加计算次数以增大统计的样本空间。

对于贴近火箭、卫星表面的羽流粒子撞击区，羽流流场密度低，不会产生复杂的流场结构，可视为自由膨胀。对该区域羽流存在的与壁面相对位置、流场非均匀、流动分离等问题，均可通过DSMC方法跟踪分子运动轨迹来实现流场特性计算。该区域的流场网格划分，通过引入分区网格和非结构网格技术，流场中使用自适应二级笛卡尔网格，火箭、卫星表面采用准确表征物面形状的非结构网格。

2　计算模型与羽流流场的划分

为便于计算实现，将卫星、火箭处理为圆柱体，所选定的计算区域可处理为去掉火箭筒体左上柱体部分的一个巨大的非规则圆柱体区域，图1为具体的计算区域示意图。

反推火箭安装于箭体侧壁距火箭上端面距离为d1的典型位置。反推火箭燃气流从喷管喷出后，在极其低压外界环境中迅速膨胀，密度急剧下降，流动状态先后经历连续流区、近连续滑移流区、过渡流区乃至高稀薄自由分子流区，同时对火箭、卫星载体表面产生沉积侵蚀影响。这类羽流流场计算网格可按照流动特征进行划分，同时根据不同的流场特征采用相应的计算方法。

图1　反推火箭燃气羽流计算区域及网格划分示意图Fig.1　Diagram of calculation area and mesh generation for spatial plume contamination in retro-rocket

3　羽流场计算状态

为考虑反推火箭在不同安装位置、不同安装角度下，燃气喷出物羽流场对卫星的影响，本文针对上述2种影响因素提出了3种不同安装形式，并对不同安装形式下反推火箭燃烧产物的羽流场进行计算分析，通过对不同安装形式下反推火箭燃烧产物羽流场计算结果进行比对分析，得到安装位置与安装角度对控制反推火箭污染的影响。

为叙述方便，定义反推火箭安装在运载火箭柱体壁面距离火箭上端面的距离为d1，反推火箭中心轴线与运载火箭中心轴线安装角为θ。具体反推火箭的3种不同安装方案列于表1所示。

4　计算结果及分析

为直观表述反推火箭各种安装状态的数密度大小和分布，将不同安装状态下反推火箭燃烧产物羽流场的计算结果分别对应列于图2～图7所示。

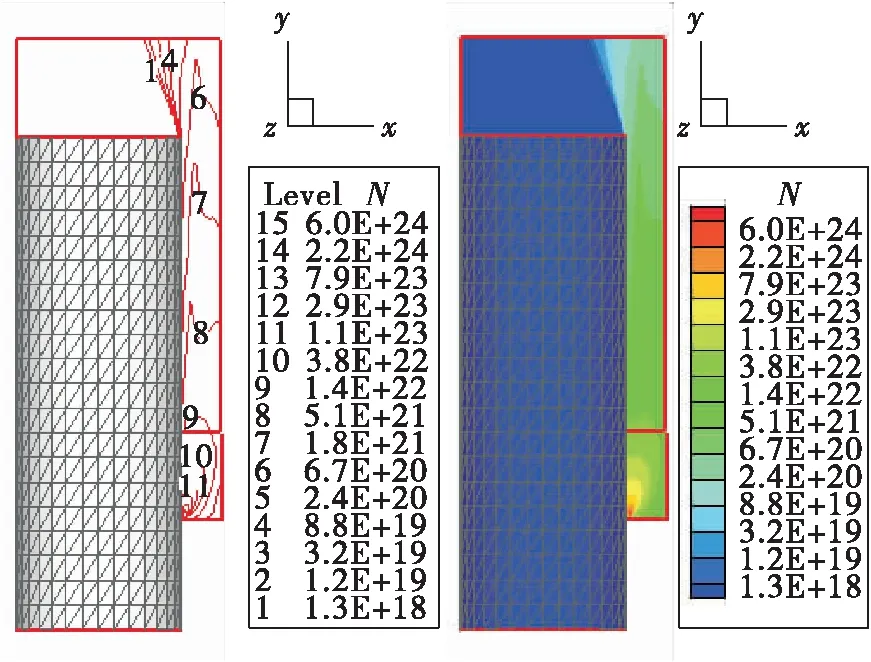
图2　状态1数密度分布Fig.2　Number density of state 1

图3　状态2数密度分布Fig.3　Number density of state 2

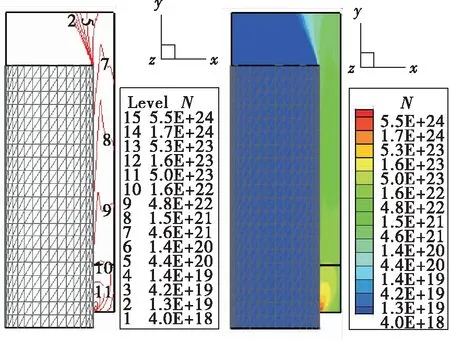
图4　状态3数密度分布Fig.4　Number density of state 3

根据以上各种状态的计算结果，将所有状态下不同位置反推火箭燃烧产物颗粒的数密度计算结果列于表2所示。

由上述数密度分布图反映出仅局部改变反推火箭安装角与安装位置，3种状态所计算得到的流场结构与流动参数变化趋势、定性分布规律基本相似。

根据图2～图7计算结果可以得到，增大反推火箭安装角与下移反推火箭的安装位置，都会使卫星载体影响区的羽流场数密度大大降低，从而减小反推火箭发动机燃气羽流对卫星载体的影响，但是过分增大反推火箭在主体运载火箭四周园柱体壁面的安装角，又会减小反推火箭提供的星箭分离有效推力。

图5　状态1数密度分布d2=2 m平面Fig.5　Number density distribution of state 1 on the d2plane (d2=2 m)

图6　状态2数密度分布d2=2 m平面Fig.6　Number density distribution of state 2 on the d2plane (d2=2 m)

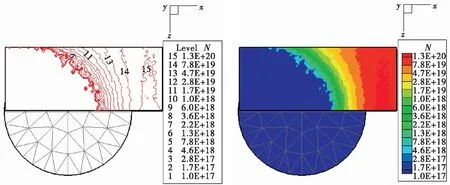
图7　状态3数密度分布d2=2 m平面Fig.7　Number density distribution of state 3 on the d2plane (d2=2 m)

.

图8　上端面(x=2 m，z=0 m)中心轴线由里向外数密度变化规律Fig.8　Number density variation from inside to outside on central axis of the upper end plane (y=2 m，z=0 m)

从图8绘出的数密度随x轴变化关系可以得到，3种状态计算得到的数密度峰值彼此差别。状态1的峰值最大，状态2的峰值其次，状态3的峰值最小。

且对于d1=7.7 m，θ=9°的状态1，其计算得到的数密度峰值约是状态2的峰值的1.6倍、约是状态3的峰值的2.7倍；

5　结论

通过上述反推火箭不同安装状态的羽流场计算结果进行分析比较表明，不同安装角与安装位置对反推火箭羽流场的计算结果会有较大影响，导致反推火箭燃烧产物对卫星污染的影响不同。因此，调整反推火箭的安装形式，是减少反推火箭羽流场对卫星污染侵蚀影响的有效途径。