高倍聚光模组系统研究与设计
黄 瑞,郭丽敏,刘友强,王聪聪,赵 明,张晓宁,张红梅,王智勇,曹银花
(北京工业大学激光工程研究院,北京 100124)
1 引 言
高倍聚光太阳能技术旨在通过采用相对便宜的光学元件来取代大量昂贵的半导体材料以降低电力成本[1]。虽然改进的余地仍然很大,但这种技术在丰富的太阳能资源和有利的经济环境下已经显示出可喜的成果[2]。梁齐兵等[3]对某一特定的三结聚光电池进行电路网络建模计算,并分析菲涅耳透镜光斑强度分布和照射面积对电池的影响;付苓等[4]针对能流分布的均匀性的问题,设计了3种可改善聚光能量分布均匀性的二次聚光器;郭丽敏等[5]成功设计出一种可拆卸的倒置的去掉顶部的棱锥形二次反射镜来提高聚光光伏接收角;杨光辉等[6]对设计的二次均光元件进行了优化,输出功率提高了16%;闫素英等[7]为了提高三结砷化镓太阳能电池芯片表面能流分布的均匀性,对菲涅耳高倍聚光PV/T系统采用正交试验法,得到光斑均匀性为89.11%、光学效率达89.29%。太阳能光伏发电依次经历了晶硅(单晶硅、多晶硅)发电技术、薄膜(CIGS、CdTe为代表)发电技术、以及第三代高倍聚光光伏(HCPV)技术。
与前两代发电技术相比,高倍聚光发电技术具有光电转换效率高[8]、光谱吸收范围宽、温度适应性好、土地利用率高、环境友好等诸多优点,已经成为当今太阳能应用领域研究的热点课题。高倍聚光发电技术的关键在于聚光系统的性能,而聚光系统的性能又与单位模组的实际发电效率密切相关。聚光系统的聚光效率和能量均匀性直接影响单位模组的发电效率。本文研究和设计出菲涅耳透镜和球冠平顶微棱镜,来提高聚光系统的聚光效率和电池表面的能量均匀性。
2 理论分析
2.1 菲涅耳透镜的设计
菲涅耳透镜具有加工简单、体积小、重量轻等优点。它的设计不同于普通透镜[9],主要采用近似有限元方法将大面积曲面透镜分成极小的环带,通过每个小环带的聚焦,最终达到聚焦的效果。本文利用边缘光线原理,即以最大入射角入射的光线可以达到电池片表面,就认为中间光线就可以入射到电池片表面。聚光系统主要考虑的是光线到达电池片表面的能量集中度和聚光效率,并不需要考虑成像质量。菲涅耳透镜的聚光原理如图1所示。
图中光线垂直入射到菲涅耳透镜的表面,光线方向不发生改变。当光线到达透镜的齿面时,光线会发生折射,折射后的光线到达太阳能电池表面。本文中设计的菲涅耳透镜厚度为2 mm,透镜的齿高y≤0.4 mm。当齿高 y≤0.4 mm 时,透镜齿之间的间隔为1 mm。当齿高y>0.4 mm时,需要调整齿间间隔和齿的角度来达到光线汇聚到电池片表面的目的。
当齿高y>0.4 mm时,根据边缘光线原理,假设光线从齿的最左侧垂直入射下来,齿的最左侧到透镜圆心的距离为P,光线与齿面形成θi的角度,太阳能电池位于菲涅耳透镜的焦点f处,太阳能电池片的半径为r,由于电池片相较于菲涅耳透镜的焦距来说很小,可以将其视为一点,到达芯片上的光线与竖直方向所成的角度都为τ,所经过折射的光线方向偏转角度为(τ+θi),由几何关系可知,齿在水平方向也成θi的角度,菲涅耳透镜的折射率为n,空气的折射率为1,齿间间隔为Δd。
根据折射率定理可得:
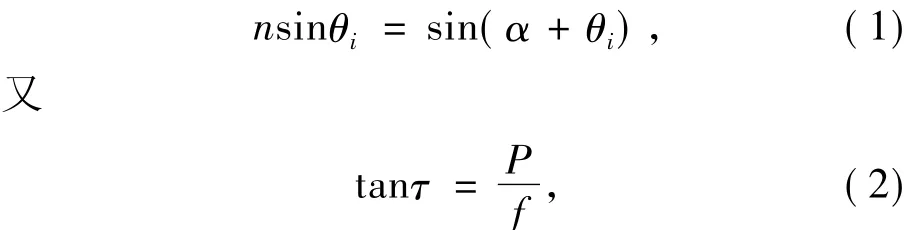
可以求出 θi的值,齿高 y=0.4 mm,则齿间间隔为:

然后将(P+Δd)作为下一个齿最左侧的距离,这个过程可以代入到Matlab中进行迭代,得出菲涅耳透镜各个齿间间隔和齿的角度的具体值。这样就可以设计出不同焦距的菲涅耳透镜满足应用需求。
2.2 球冠平顶微棱镜的设计
2.2.1设计方案研究
球冠平顶微棱镜的结构如图2所示,棱镜的下面仍然采用正四棱锥的结构[10],上面为球面和平面的组合,作为太阳光的入射面,小底面作为太阳光的出射面,小底面的面积与太阳电池片的面积相当,4个侧面为全反射工作面。为了减少反射能量损失,设计时要求光线在侧壁上发生一次全反射后就到达太阳能电池的接收面上。

图2 球冠平顶微棱镜结构示意图

设空气折射率为n1,球冠平顶微棱镜折射率为n2,参考折射定律和几何关系可知:
设球冠平顶微棱镜两边与圆心的夹角为α,入射光线和球冠交点与球圆心的连线与OH的夹角为β。在△ABO中,由正弦定理可知,
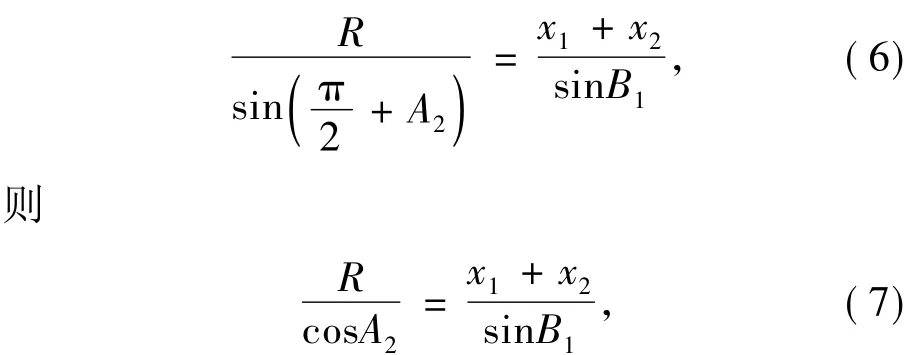
在△EIO中,由正弦定理可知,
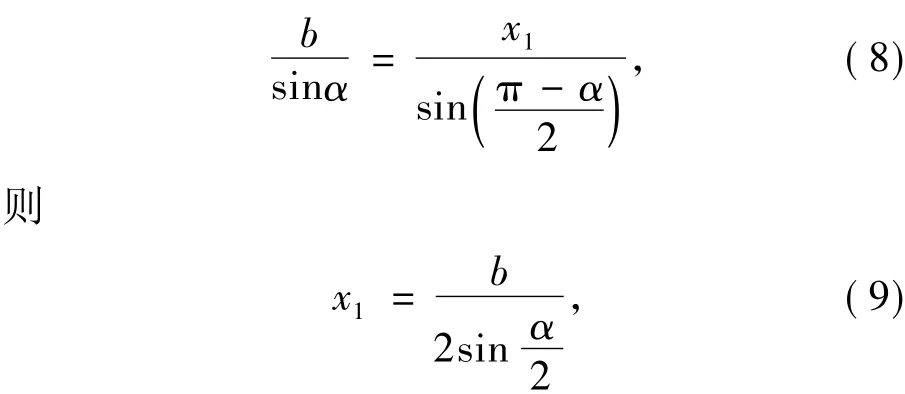
由公式(4)可知,
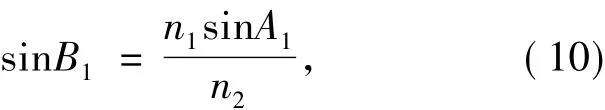
将公式(10)带入公式(7)得:
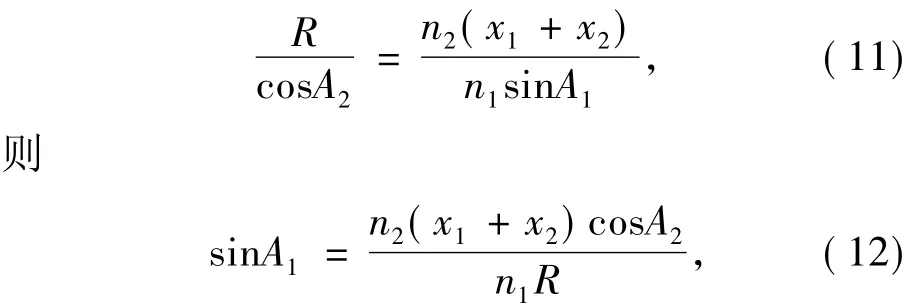
在△BEI中,由正弦定理可知,
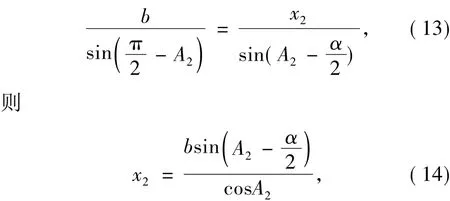
由公式(9)、(12)、(14)可得
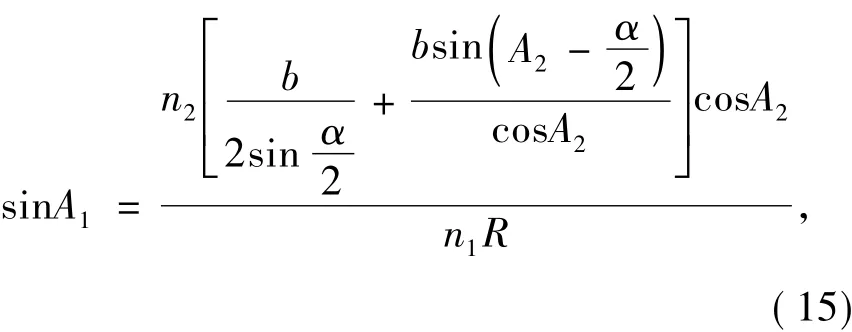
光线在B点发生全反射,由全反射定理可知,
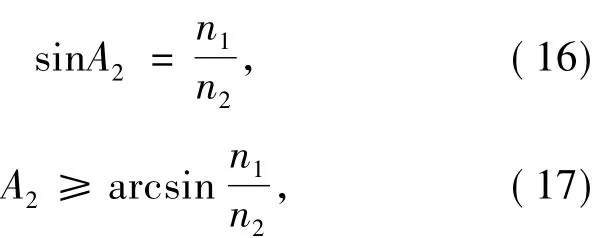
由公式(15)、(17)可得

如图2所示,入射A点的光线,经B点反射到达I点,要求所有光线经过一次反射后能到达EI表面,则BE的长度x≤x2,即入射角A≤A1。(20)就可以得出进入球冠平顶微棱镜球面处光线入射角与球冠二次镜α、R、b之间的参数要求,从而保证了球冠平顶微棱镜球面处的聚光效果,以此作为二次光学元件设计的理论依据。

球冠平顶微棱镜是将球冠顶磨平,可以显著改善入射到太阳能电池片的能量均匀性。垂直入射到平顶的太阳光线没有经过侧面发射到达太阳能电池片上[11]。
经过球冠平顶微棱镜的光线可直接到达电池片表面,或经过侧面反射一次后到达电池接收面,其聚光效果同微棱镜结构[12],即要求入射角为A'1的光线需满足以下条件:
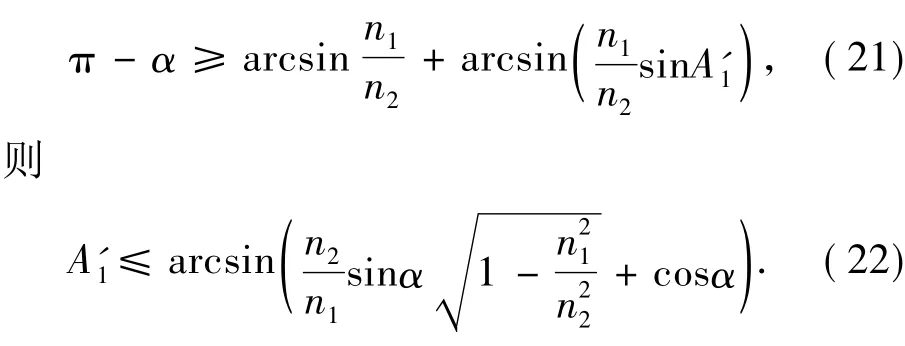
如图2所示,设A点为球冠平顶的分割点,由几何关系及公式(17)可知,
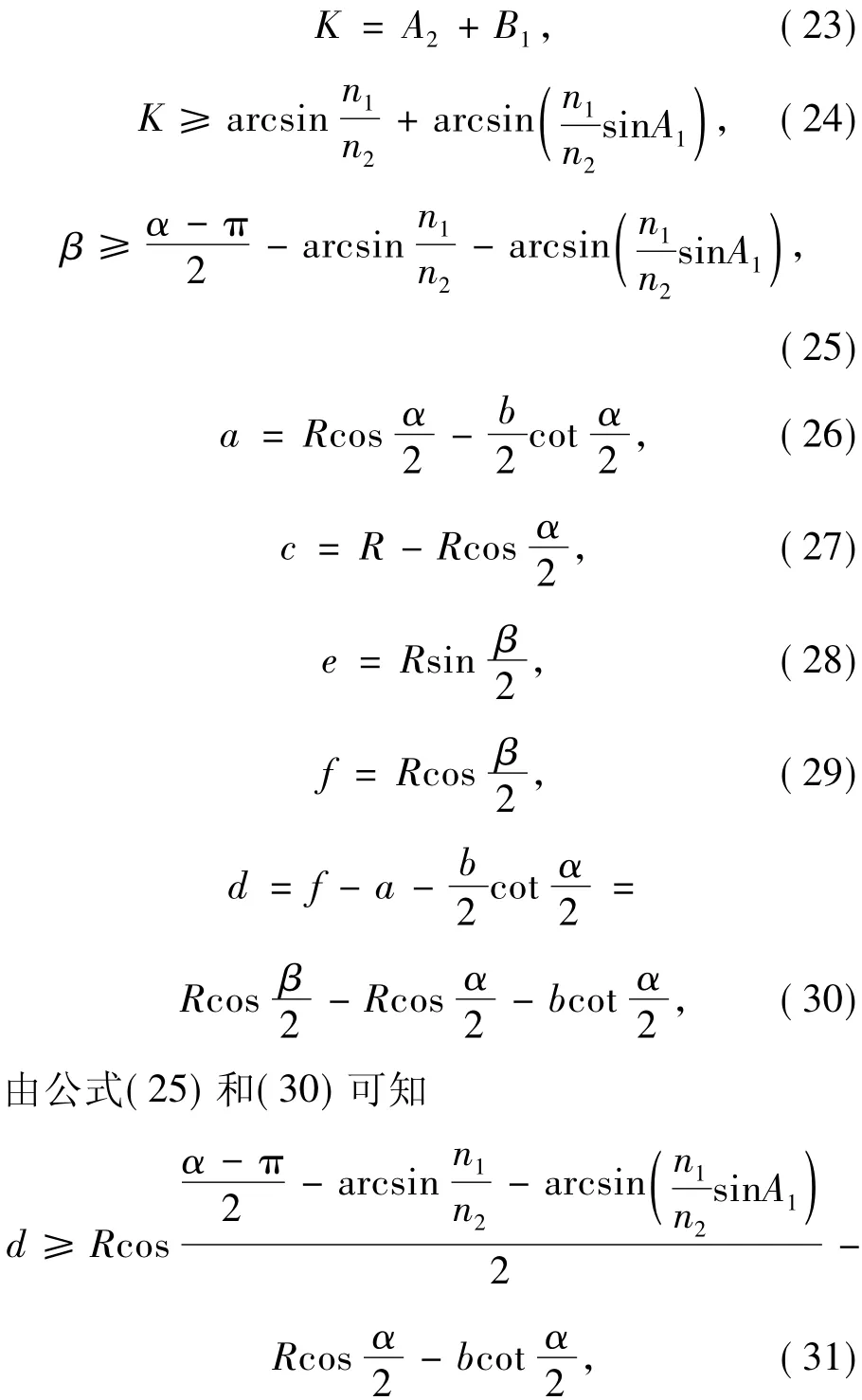
由此可见,入射角A'1确定后,即可求出球冠平顶
到球面棱边的距离d。
2.2.2球冠平顶微棱镜模型
图3所示为球冠平顶微棱镜的三维模型示意图,下底面边长为b,平顶到球面的距离为g,球面半径为R,球冠两侧面的夹角为α。
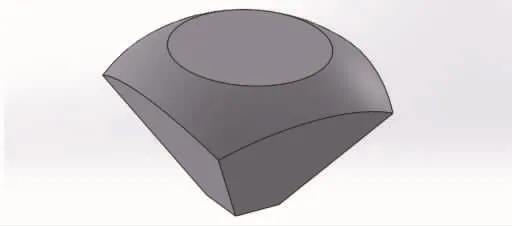
图3 球冠平顶微棱镜三维模型示意图
3 模拟与实验
3.1 576倍模组聚光系统的设计模拟
我们可以将设计好的菲涅耳透镜和球冠平顶微棱镜的各项参数导入Solidworks中,建立菲涅耳透镜和球冠平顶微棱镜组成的聚光系统三维模型,结构如图4所示。

图4 聚光系统的三维模型
576倍模组聚光系统由菲涅耳透镜和球冠平顶微棱镜组成[13]。其中,菲涅耳透镜的初始参数是厚度为2 mm,齿高y≤0.4 mm部分,透镜齿之间的间隔为1 mm;齿高y=0.4 mm的部分,调整齿间间隔和齿的角度使得光线汇聚在电池片上。另外,为了便于后期组装,我们将圆形的菲涅耳透镜切成其内接正方形,尺寸为60 mm×60 mm。576倍模组聚光系统对应的菲涅耳透镜的焦距为108mm,太阳能电池片的尺寸为2.5 mm ×2.5 mm。将设计好的聚光系统导入进Zemax系统中,利用Zemax的非序列模式进行聚光系统的光路分析。系统在Zemax中的结构如图5所示。

图5 Zemax中的聚光系统的光线模拟图
影响球冠平顶微棱镜的聚光效果主要有3个因素[14]:平顶到球面的距离 g、棱镜两侧面的夹角α以及球冠的半径R。下面我们将利用Zemax进行电池表面能量均匀性和接收效率的分析,采用控制变量法分别确定3个方面的值。最终设计出最佳的球冠微棱镜结构。其中菲涅耳透镜在Zemax中采用硅酮材料,球冠采用K9玻璃,Zemax中模拟的总能量为3.6 W。
3.1.1两侧面夹角α的优化
在研究两侧面夹角对球冠的影响过程中,我们保持平顶到球面的距离g=0,球冠的半径R=9 mm,两侧面的夹角取 100°~140°,每间隔 1°取一个测量值。计算结果部分的能量值如表1所示;两面夹角与能量值之间的关系曲线,用origin软件画出,如图6所示。
软件仿真可得,当平顶到球面的距离g=0,球冠的半径R=9 mm时,两侧面的夹角α为112°到122°之间时,到达太阳能电池片上的能量值比较高。同时,我们在模拟的过程中发现当只改变球冠平顶微棱镜的两侧面夹角时,探测器上光斑能量的均匀性并没有提高,而且计算得出的能量均匀度并不高。
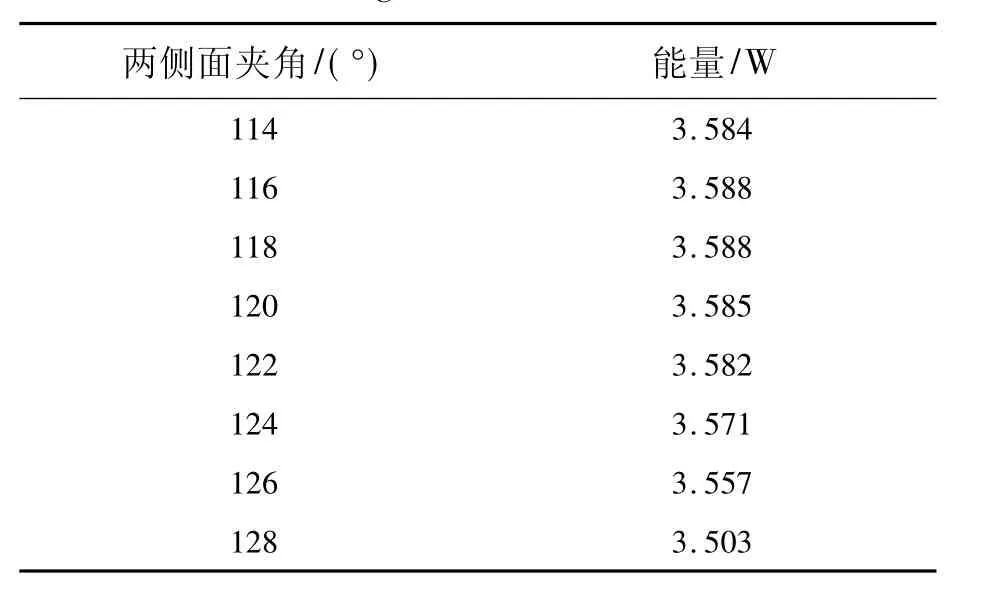
表1 不同两侧面夹角对应聚焦光斑能量值Tab.1 Energy value of focusing spot corresponding to different two side angles
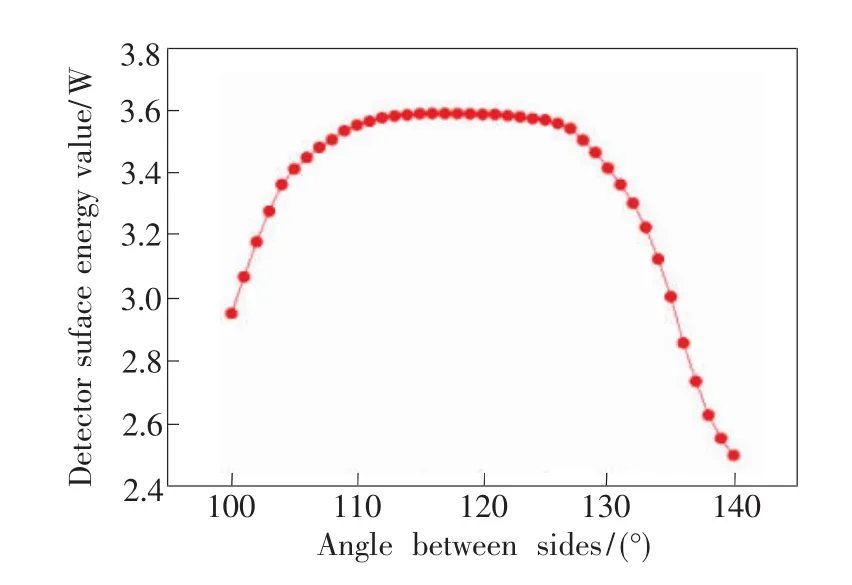
图6 两侧面夹角与聚焦光斑能量值的对应关系
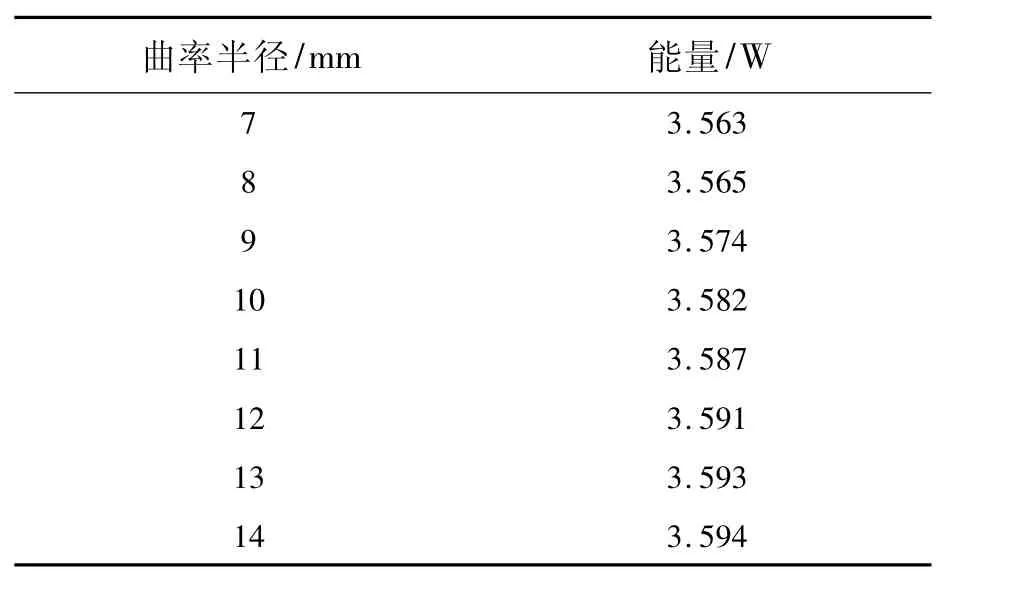
表2 不同曲率半径对应的聚焦光斑能量值Tab.2 Energy value of focusing spot corresponding to different radius of curvature
3.1.2曲率半径的优化设计
设球冠两侧面的夹角α为120°,平顶到球面的距离为0mm,此时的球冠平顶微棱镜为球冠二次棱镜,对棱镜的曲率半径进行优化设计,R的取值范围为7~14mm,每隔1mm测量一次,利用Zemax进行模拟计算,得出聚光能量值,测量出的值如表2所示;图7为曲率半径R与聚焦光斑能量值的对应关系。
根据变化曲线可知,曲率半径R越大,在电池片上的聚光能量值越高,但是当R>9 mm时,能量随着曲率半径变化不大。考虑到加工方便等因素,曲率半径R取10 mm。
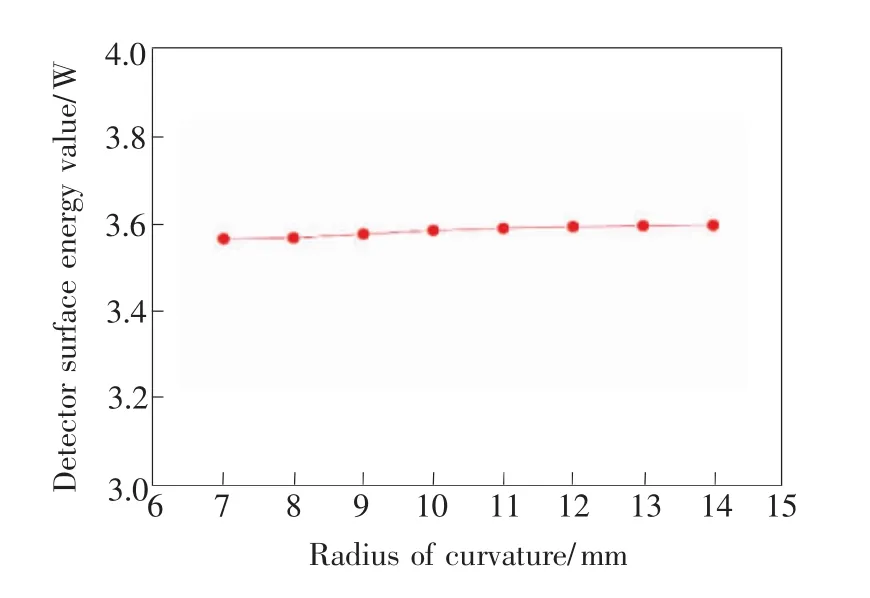
图7 曲率半径与聚焦光斑能量值的对应关系

表3 不同间隔g对应的聚焦光斑能量值Tab.3 Energy value of focusing spot corresponding to different intervals
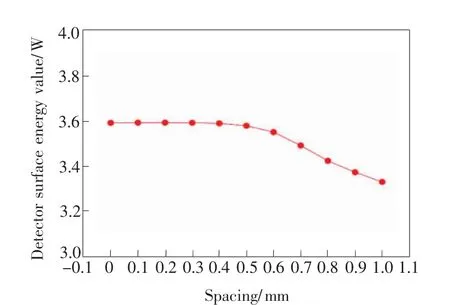
图8 平顶到球面的间距与聚焦能量的对应关系
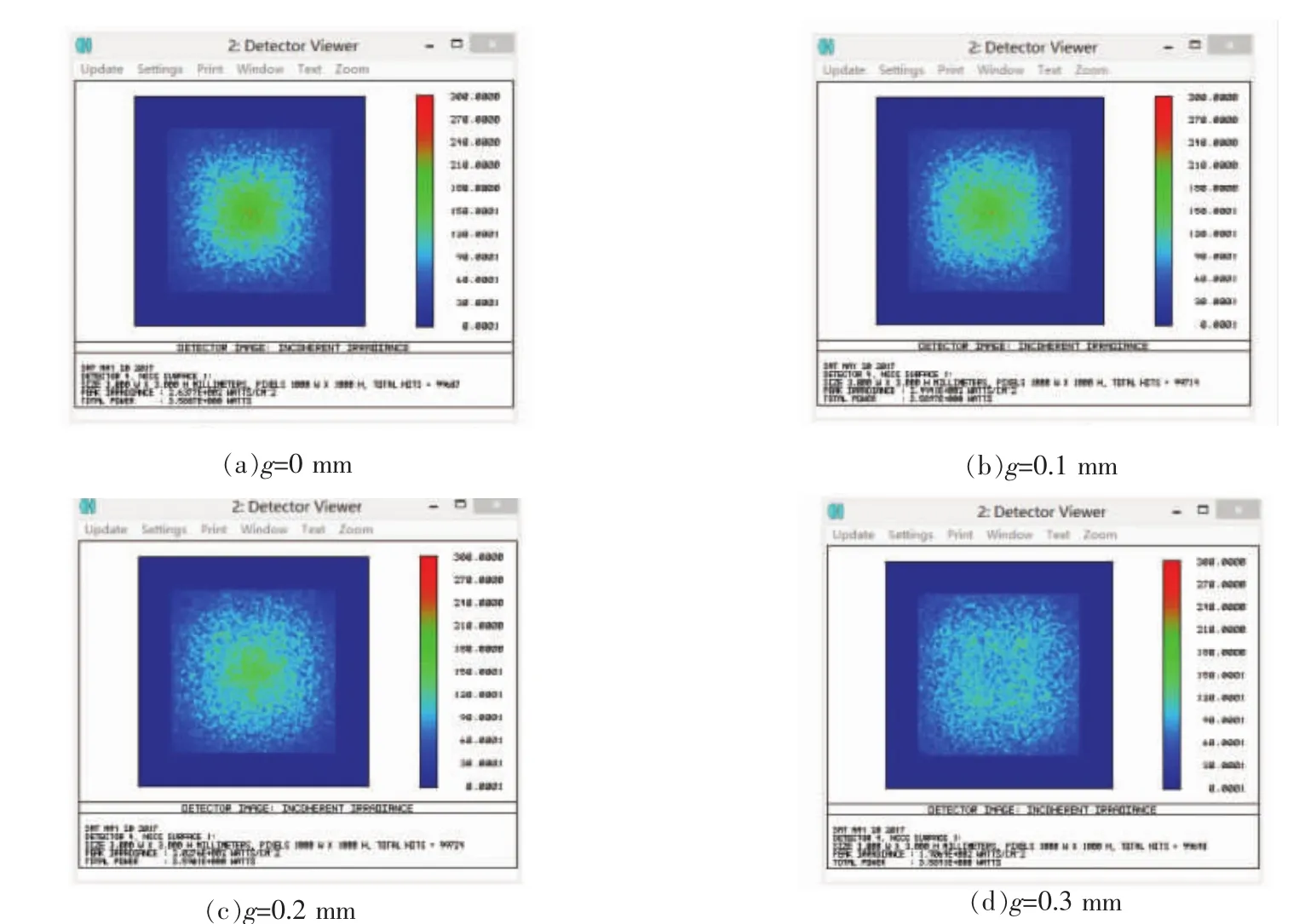
图9 不同间距处对应的能量均匀性变化情况
3.1.3平顶到球面间距g的优化
取球冠的曲率半径R为10 mm,两侧面夹角α为120°,利用Zemax对球冠微棱镜的平顶到球面的间距进行模拟。平顶到球面的间距g从0取到1 mm,模拟的聚焦光斑能量值如表3所示,用origin软件画出平顶到球面间距g与聚焦光斑能量值的变化曲线如图8所示。
从模拟的结果能够看出,平顶到球面的间距对系统的聚光效果影响明显。此外,在Zemax的模拟过程中,间距对入射到电池片的光线的均匀性也有较为明显的改变。这里我们选取间距g=0,0.1,0.2,0.3 mm 时,探测器上光线强度的分布情况如图9所示。综合聚光能量和聚光均匀性两方面考虑,我们取间隔g为0.2 mm。
3.1.4聚光系统整体优化设计
根据以上模拟确定球冠的曲率半径R=10 mm,间隔 g=0.2 mm,球冠两侧面的夹角 α为116°~120°,菲涅耳透镜的焦距为108 mm。为了能够最终确定最佳的聚光系统,我们再次对两侧面夹角进行优化分析,不同角度对应的能量值如表4所示。同时我们也计算了在不同角度处,入射到探测器表面的能量均匀性的大小。聚焦光斑能量的均匀性为平均辐照度与最大幅照度之比,不同角度对应的能量均匀性的大小如表5所示。

表4 不同角度对应的聚焦光斑能量值Tab.4 Energy value of focusing spot corresponding to different angles

表5 不同角度对应的能量均匀性的大小Tab.5 Magnitude of energy uniformity corresponding to different angles
综合考虑聚焦光斑能量值和能量均匀性两个因素,决定选取两侧面夹角α的角度为117°,平顶到球面的间隔g为0.2 mm,球冠平顶微棱镜的曲率半径R为10 mm。此时,Zemax模拟的总能量为3.6 W,测出的能量为3.588 1 W,因此理论聚光效率为99.7%。
3.2 聚光系统实验研究
3.2.1实验对象确定
我们根据仿真模拟确定球冠平顶微棱镜相关参数,研制出球冠平顶微棱镜,它的实物图如图10所示;并在此基础上,研制出高倍聚光模组的实际产品,如图11所示。

图10 球冠平顶微棱镜的实物图

图11 高倍聚光模组实物图

图12 聚光模组测试系统
3.2.2实验方案和结果
本文采用高聚光型太阳能组件室内测试系统来对聚光模组进行静态效率I-V测试[15]。高聚光型太阳能组件室内测试系统由闪光发光器件、反射光板、模组功率测试仪等组成。系统专门配备有相应的测试软件,用来记录数据。我们对579倍聚光模组进行测试,所用的太阳能电池效率为40%,光强设置为850 W/m2,温度为常温25℃。将发电模组放入测试机台如图12中,即可进行发电单元的最大输出功率Emax测试,共测试10次,测试结果如表6所示,典型I-V测试曲线如图13所示。
从图中可以看出,测试结果的最大平均输出功率为135.6W。太阳能电池效率为40%,光强设置为850W/m2,可以计算出聚光系统的聚光效率为83.1%。但由于存在棱镜的透过损失、菲涅耳透镜加工的误差以及光学元件折射率分布不均匀等因素影响,实际的聚光效率比理论的聚光效率小,这符合实际情况。同时入射在太阳能电池片的能量均匀性为0.812。

表6 输出功率测试结果Tab.6 Test results of output power
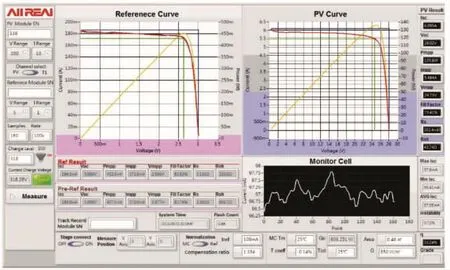
图13 典型的I-V测试曲线
4 结 论
本文研究和设计了一种高倍聚光发电模组,分别对模组中的菲涅耳透镜和球冠平棱镜进行研究。确定了菲涅耳透镜的具体设计参数,并分别讨论了球冠平顶微棱镜的曲率半径、两侧面夹角和平顶到球面的间隔对棱镜聚光能力的影响。最终决定选取两侧面夹角为117°,平顶到球面的间隔为0.2 mm,球冠平顶微棱镜的曲率半径为10 mm。模拟测出系统的聚光效率为99.7%,能量均匀性为0.812。最后进行实验,实际测出的聚光效率为 83.1% 。

