均匀重力场中质点在光滑圆柱面上的挠曲线运动
李 力
(重庆清华中学,重庆 400054)
在理论力学和分析力学课程里,通常研究质点的平面曲线运动。这些做平面曲线运动的质点,多数被约束在二维平面上,也有一些被约束在二维曲面上。约束在二维曲面上发生的一般的空间挠曲线运动,却很少涉及。空间曲线不仅有弯曲的性质,而且还有扭转从而离开平面形式的性质。前一性质用曲率描述,后一性质则用挠率刻画。平面曲线的挠率恒等于零,反之,挠率恒等于零的曲线必是平面曲线。所谓挠曲线,就是挠率不恒为零的曲线[1],这种空间挠曲线运动的处理,不可避免地要用到更多的数学方法,比如微分几何的曲线、曲面论,某些特殊函数的知识等。
本文研究了均匀重力场中的质点在光滑圆柱面上的挠曲线运动,用牛顿定律或拉格朗日方程推导质点的运动微分方程,然后解得质点脱离圆柱面的位置满足的方程以及脱离前的运动时间,最后导出用椭圆积分表示的挠曲线运动轨迹的参数解析表达式。
1 质点在光滑圆柱面上的运动微分方程
在如图1所示的光滑1/4圆柱面以及圆柱坐标系(ρ,φ,z)中,质点的初位置在圆柱面的最上端A(R,0,0),初速度v0在过A点的水平切面内,与Oz轴夹角为α,沿Oz、Oy轴的分速度分别为v1,v2。显然有初始条件̇z0=v1=v0cosα,Ṙφ0=v2=v0sinα,即
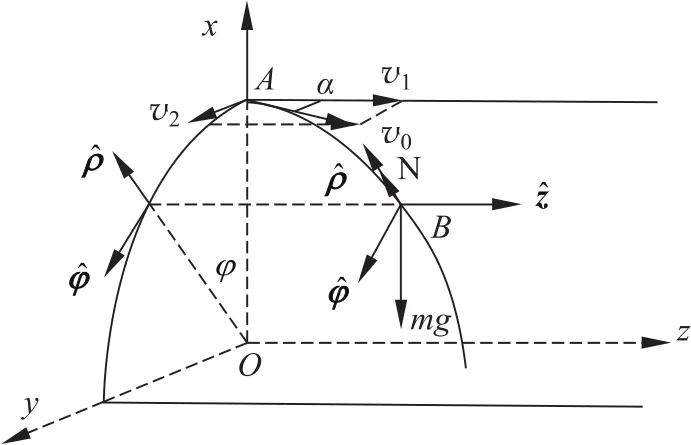
图1 质点在光滑圆柱面上的挠曲运动
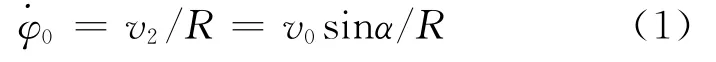
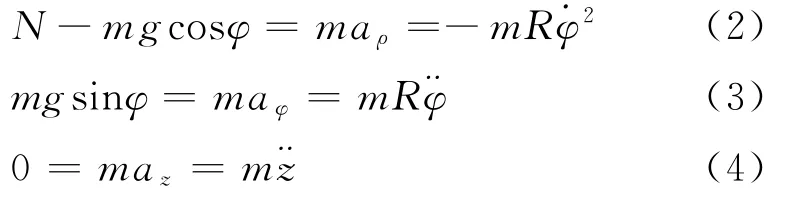
顺便指出,用拉格朗日方程也可以简便地推导出(3)、(4)两式,此处不再赘述。
2 z和̇φ的推导
由式(4)积分,并考虑初始条件,得̇z=v1,故
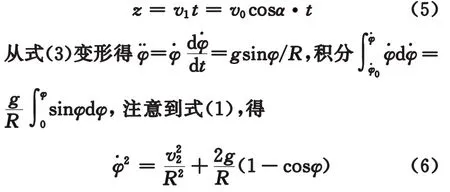
因̇φ>0,故取
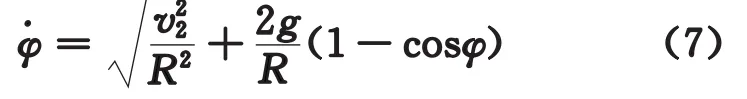
3 脱离位置与脱离时间
将式(6)代入式(2),并令 N=0、φ=φm,有
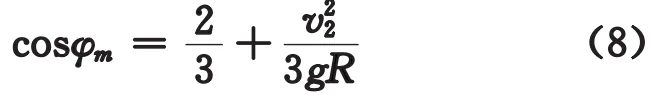
由于在A点不脱离圆柱面,须v2< g R,从而式(3)右端另外,若v=0,则脱离2位置cosφm=,这正是理论力学课程中熟悉的结论[3]。
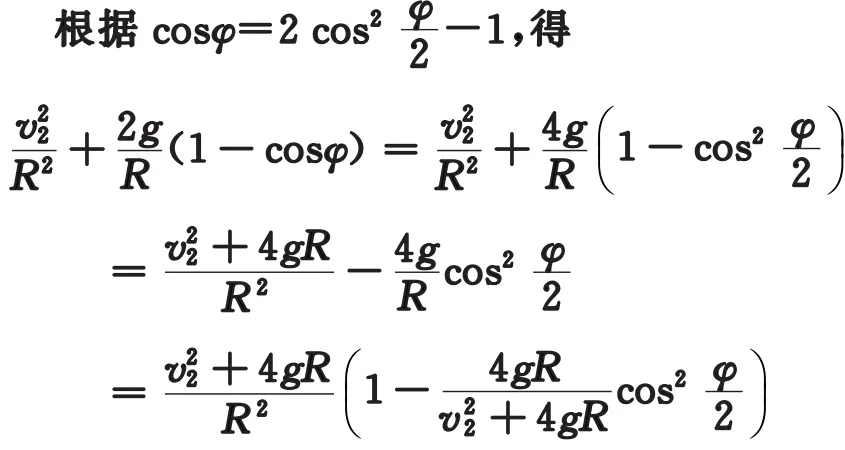
故式(7)化为

得到脱离时间
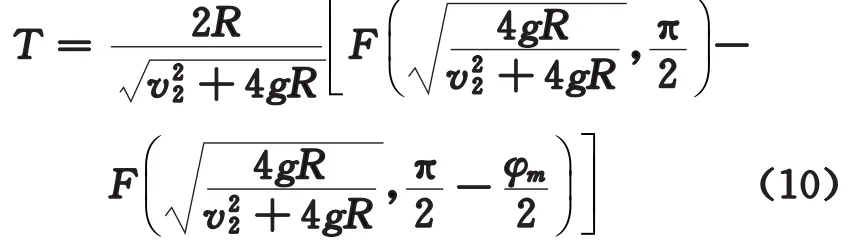
其中F(k,φ)是勒让德第一类椭圆积分[4],即而φm由式(8)定出。
4 运动轨迹方程的解析表达式
为了得到在圆柱面上的运动轨迹方程,只需在式(10)中作代换T→t,φm→φ,并同式(5)联立,即得用椭圆积分表示的挠曲线运动轨迹的参数解析表达式为
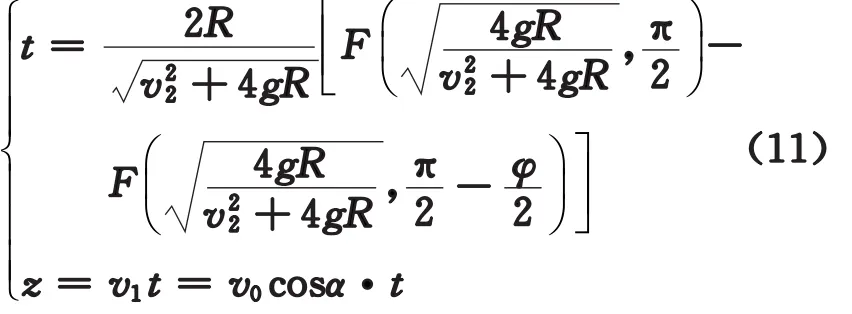
或者直接写成
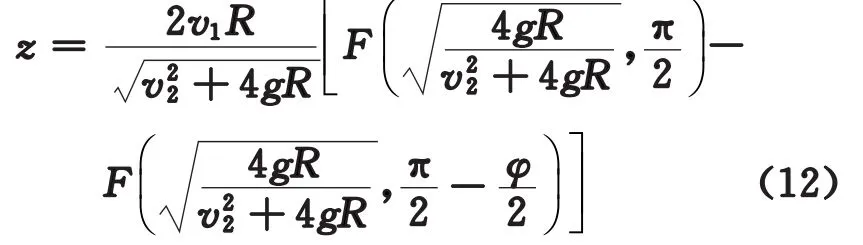
按照微分几何曲线论[1],得到运动轨迹在直角坐标系中以时间t为参数的曲线表达式为

如果以z为参数,则曲线的参数方程可写为
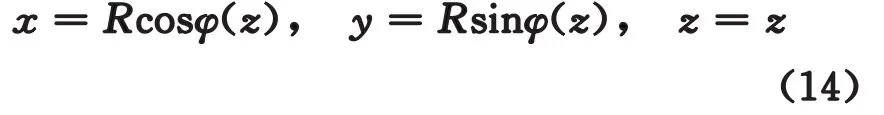
其中φ(t),φ(z)分别是由式(11)和式(12)所定义的φ与t、φ与z之间的函数关系。
5 结语
研究均匀重力场中的质点在光滑圆柱面上的挠曲线运动,有一定的理论意义和应用价值。本文用牛顿定律或拉格朗日方程推导质点的运动微分方程式(2)~(4),然后解得质点脱离圆柱面的位置满足的方程(8)以及脱离前的运动时间式(10),最后导出用椭圆积分表示的挠曲线运动轨迹的解析参数表达式(11)~(14)。
因为圆柱面上过A点的沿v0方向的平面截线是椭圆,而式(11)~(14)表明运动轨迹并非椭圆,所以质点做挠曲线运动;又由变分法可知,圆柱面上的测地线(即短程线)是螺旋线[5],故质点的运动轨迹也不是测地线。另外,用微分几何可以证明,在只受曲面法向约束力时,质点必沿测地线运动[6],而我们讨论的本问题还要考虑均匀重力场的作用,因此更为复杂。由此可以看出,均匀重力场中的质点,在任意形状的光滑曲面上的空间挠曲线运动,求解起来有相当的难度,一般而言是不容易得到或者根本不存在解析表达式的。
——目镜套筒

