四参数Logistic模型和传统模型对被试作答拟合能力的比较研究

刘　玥　刘红云

(北京师范大学心理学部，北京 100875)

1　前言

1.1　测验中的睡眠现象

在成就测验中，存在着一种高能力被试答错容易题目的“睡眠现象(sleeping phenomenon)”(Wright，1977)。造成这种现象的原因可能有：焦虑、不良的测试环境导致被试分心、粗心、误解题意，测验动机过强和家长期望压力过大等。同时，在心理测验(如人格测验)中，也存在一种由于被试掩饰、说谎等原因，在试题上表现出人格特征维度低水平方向的倾向性作答，使得被试在这一人格特征维度上总分偏低的现象(简小珠，焦璨，彭春妹，2010)。睡眠现象会导致测验总分偏低，从而造成测量偏差。在项目反应理论下，为了对睡眠现象进行修正，McDonald(1967)最早提出使用参数来反映一部分高能力被试答错了容易试题的现象。睡眠现象可能会单独出现。例如，对于一些难度较大的填空题，高能力被试未必能全部答对，而低能力被试则很难猜对。这时可以使用含有难度、区分度和睡眠参数(上渐近线参数)的三参数Logistic模型拟合数据。另外，睡眠现象和猜测现象可能同时出现，这时可以在传统IRT模型(以下简称传统模型)基础上加入睡眠参数，来反映数据结构。

1.2　四参数Logistic模型介绍

1.2.1四参数Logistic模型定义

Waller和Reise(2010)在最早的四参数Logistic模型基础上进行拓展，提出了广义模型。该模型中每道题目的睡眠参数是不同的。

其中，aj，bj，cj分别表示区分度、难度、猜测参数。dj表示睡眠参数，在传统模型中，dj固定为1，而在此模型中，dj可以小于1且在题目间变化。

另外，如果测验中仅存在睡眠现象而不存在猜测现象，则可以使用含有难度、区分度和睡眠参数的三参数logistics模型(Waller & Reise，2010)。

1.2.2四参数Logistic模型估计

四参数Logistic模型在产生初期应用并不广泛，这主要是由于传统的极大似然估计方法很难实现该模型的参数估计(Waller & Reise，2010)。而贝叶斯估计方法对于估计复杂、多参数的模型非常有效。因此，Loken和Rulison(2010)使用贝叶斯估计方法实现了对四参数Logistic模型的参数估计。

1.2.3四参数Logistic模型应用

在Barton和Lord(1981)的研究中，将四参数Logistic模型应用于成就测验。但是测验极大似然值没有显著增加，被试能力估计值没有显著的变化，四参数模型还增加了计算的复杂性。因此，他们不提倡使用该模型。在之后的近二十年里，关于该模型的研究论文几乎没有，该模型只在一些教材中被提及。在此期间的BILOG、MULTILOG等软件都没有相应程序模块(简小珠，张敏强，彭春妹，2010)。

直至近几年，研究者开始关注心理测验中的睡眠现象和四参数Logistic模型。2003年，Reise和Waller(2003)在分析人格测验MMPI-2 时，发现了一些试题存在睡眠现象，建议使用四参数Logistic模型拟合数据。简小珠、戴海崎和彭春妹(2007)在分析高考数据时，发现了一些试题同时存在猜测现象和睡眠现象，或单独存在猜测现象和睡眠现象。目前，关于四参数Logistic模型在成就测验中的应用主要关注CAT测试中高能力被试在初始阶段答错容易试题后，该模型对能力值低估的修正作用(Rulison & Loken，2009)。但是，国内外关于四参数Logistic模型的文章还较少，尤其国内关于该模型在实际数据中应用的研究则更少(简小珠，2006)。

1.3　研究目的

对于四参数Logistic模型的研究，大多关注了该模型与传统模型在估计结果和信息量上的差异。研究多以四参数Logistic模型模拟作答反应，以睡眠现象作为既定的前提。然而，在实际的测验中，睡眠现象真实发生的频率如何？四参数Logistic模型与传统模型的估计结果到底存在多大区别？还需要在实证研究中寻找答案。另外，关于四参数Logistic模型的应用研究多针对成就测验或心理测验中的一种，并且多数认为该模型更适用于心理测验。那么，在成就测验中，四参数Logistic模型是否对于模型拟合和参数估计没有显著改善呢？研究以焦虑量表和两种分布的数学测验为例，同时比较了在心理测验和成就测验中，四参数Logistic模型和传统模型在模型拟合和参数估计值上的结果，分析了四参数Logistic模型的必要性，提出了应用建议。

2　方法

2.1　测量工具及被试

心理测验选择了泰勒焦虑调查量表(Taylor Manifest Anxiety Scale)，共有50道题目，所有题目都要求被试回答是或否，因此均为0/1计分。被试共计5410名，其中男性占44.27%，女性占55.73%，年龄为30.12±11.87，被试得分呈负偏态分布。

成就测验选择了某大规模数学测验，共60道题目，均为有4个备选答案的单项选择题，0/1计分，满分为60分。参加测验的学生为来自47所学校的4882名高一学生，总分偏度为0.097，基本符合正态分布。

从数学测验得分小于30分的学生中随机剔除50%，构造一个新样本，其样本量为3740人，偏度为-0.199，得到一个相对原有分布的负偏态分布，以考察含有睡眠参数模型的优势是否能够在负偏态分布的成就测验中显现。

泰勒焦虑调查量表和数学测验的描述统计结果如下表：

2.2　比较模型

使用R中的sirt软件包(Robitzsch & Robitzsch，2015)进行模型与数据的拟合。拟合的模型有以下七种。

模型1：Rasch模型

模型2：两参数Logistic模型(2PM)。

模型3：三参数Logistic模型(3PM)，含有难度、区分度和猜测参数的Logistic模型。

模型4：三参数睡眠logistics模型(3PMR)，含有难度、区分度和睡眠参数的logistc模型。适用于睡眠现象单独存在的情况。

模型5：四参数Logistic模型(4PM)，同时含有难度、区分度、猜测参数和睡眠参数的Logistic模型。

模型6：模型5的基础上将所有题目猜测参数固定相等估计的模型(4PMc)。

模型7：模型5的基础上将所有题目睡眠参数都固定相等估计的模型(4PMd)。

3　结果

3.1　不同模型拟合指标结果

表2列出了对于不同数据，各模型的拟合指标结果。AIC、BIC结果具有较高的一致性。对于所有测验来说，Rasch模型的拟合结果均最差，对于泰勒焦虑调查量表，3PMR的AIC指标最好，2PM的BIC指标最好；对于原始的和构造的负偏态数学测验，4PM的AIC指标最好，4PMd的BIC结果最好。由于这两个拟合指标均考虑了模型的复杂程度，因此，综合来看，上渐近线参数非1的模型能提供较好的拟合结果。

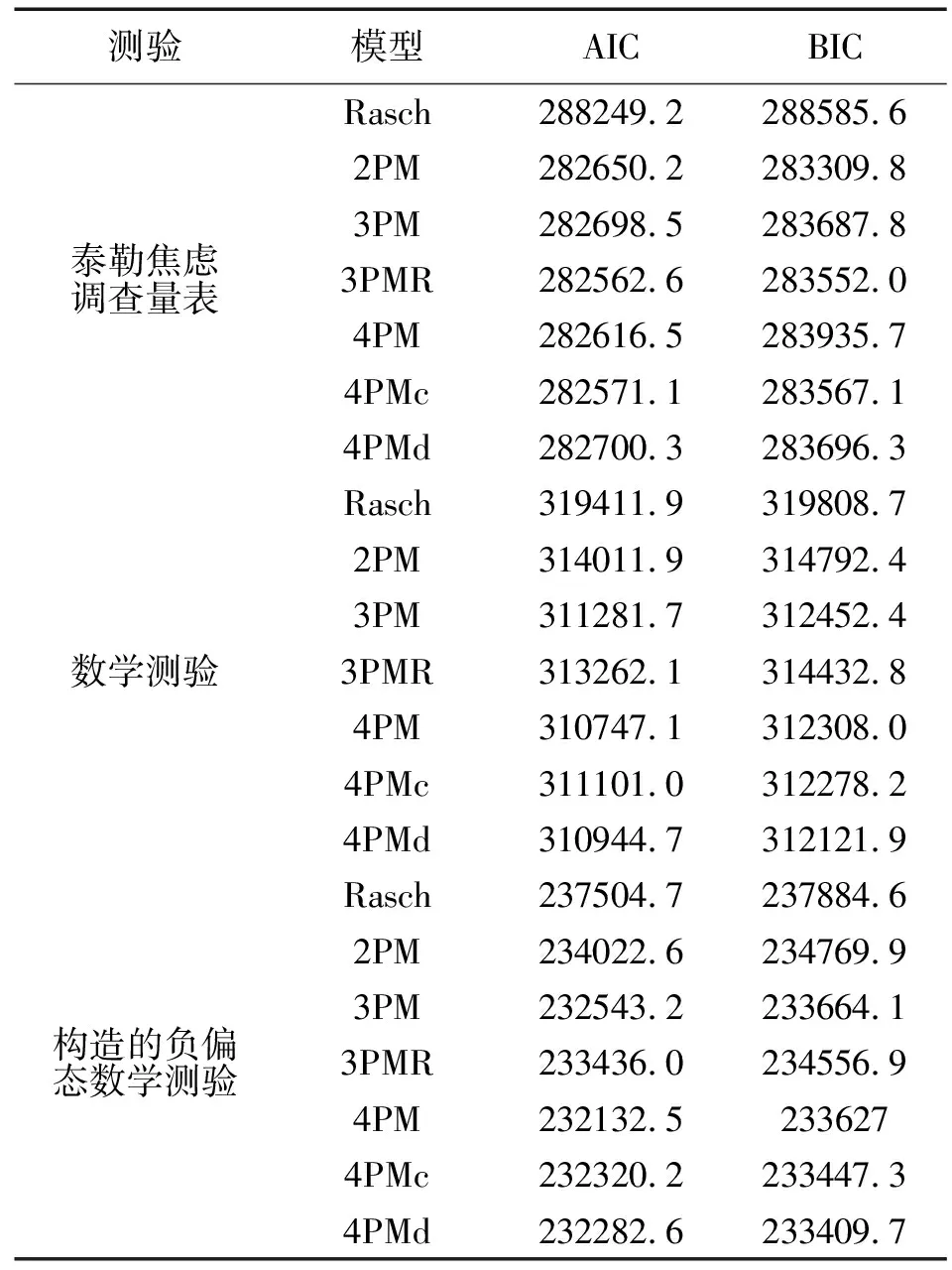
表2　不同测验模型拟合结果

3.2　不同模型参数相关

为考察四参数Logistic模型与传统模型参数估计结果的差异，计算了拟合情况最好的四参数Logistic模型(或上渐近线参数非1的模型，以下简称四参数Logistic模型)与拟合情况次之的上渐近线参数固定为1的传统模型的题目参数、能力参数的相关。

3.2.1题目参数相关

表3列出了不同测验四参数Logistic模型与拟合情况最接近的传统模型题目参数估计值的相关。

表3　四参数Logistic模型与传统模型题目参数估计值相关

从以上结果可以看出，对于不同测验，四参数Logistic模型与传统模型的难度参数估计结果具有较高的一致性，但是区分度参数具有较大的差异，并且，对于构造的负偏态数学测验，不同模型区分度参数估计值差异最大。不同模型区分度参数估计值的差异如图1所示。

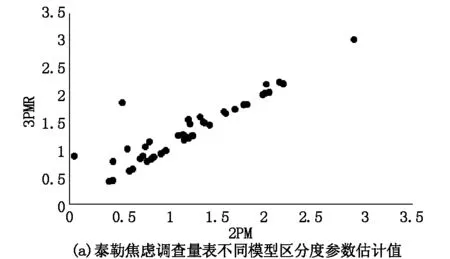
图1　四参数Logistic模型与传统模型区分度参数估计值

从图中可以看出，四参数Logistic模型得到的区分度参数估计值高于传统模型。

表4列出了按照四参数Logistic模型的难度参数估计值，删除最简单的5、10、15道题目后，不同模型参数估计值的相关。

表4　删除简单题目后四参数Logistic模型与传统模型题目参数估计值相关

从表中可以看出，删除简单题目对难度参数估计值的相关没有显著影响。但是，随着删除简单题目数量增加，不同模型区分度参数的一致性增强，该现象对于构造的负偏态数学测验尤其明显。这可能是由于简单题目数量越少，睡眠现象发生的概率相对越少，则上渐近线参数为1的情况更为普遍，因此，四参数Logistic模型与传统模型区分度参数估计值越接近。

3.2.2能力参数相关

表5列出了不同测验四参数Logistic模型与拟合情况最接近的传统模型所有能力参数估计值、部分能力参数估计值的相关。

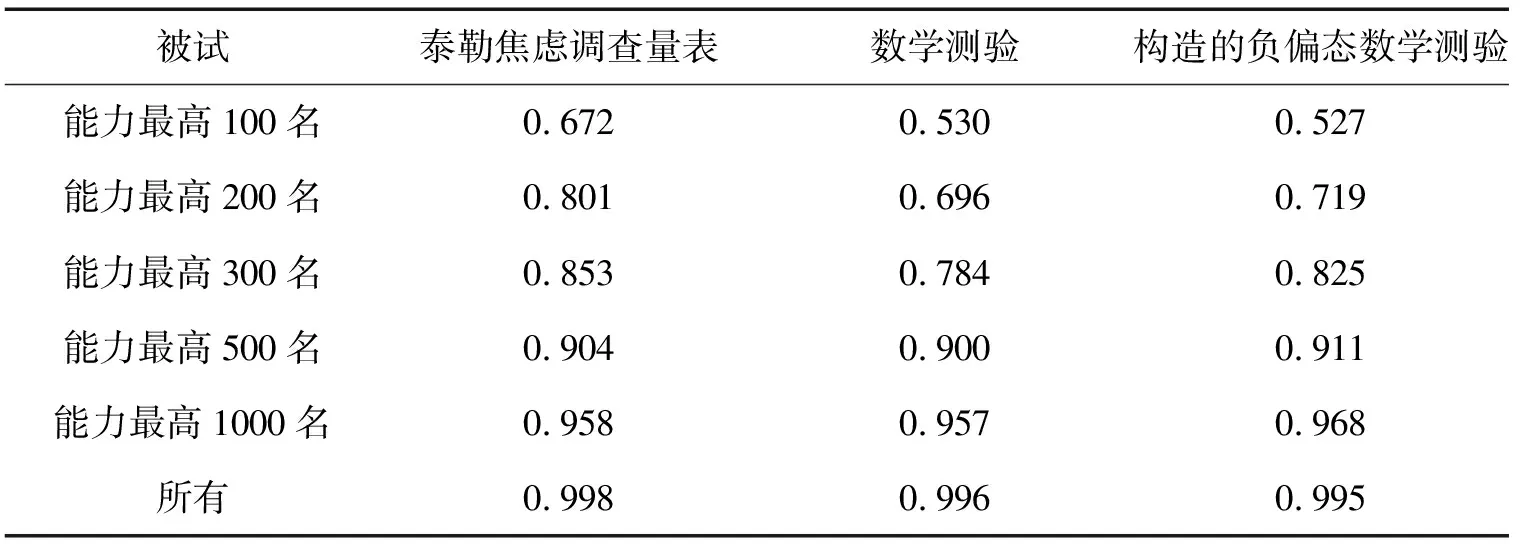
表5　四参数Logistic模型与传统模型能力参数估计值相关

注：不同测验所比较的模型与表3一致。

从结果可以看出，虽然对于所有的被试，不同模型能力参数估计值相关很高，但是对于能力越高的群体，不同模型能力参数估计值的一致性越低，特别是对于能力最高的100名被试，不同模型能力参数估计值的相关仅为0.672、0.530和0.527，对于高能力被试，四参数Logistic模型得到的能力参数估计值高于传统模型。

以数学测验为例，选取了四参数Logistic模型能力参数估计值为1以上、2以上的被试，并分别计算了对于这些群体，使用4PM和3PM得到的能力参数估计值的相关。结果显示，对于所有被试、能力为1以上被试、能力为2以上被试，两种模型能力参数估计值的相关分别为0.996、0.942、0.590。进一步验证了对于能力水平越高的被试，四参数Logistic模型与传统模型能力参数估计值差异越大。另外，如图2所示，对于高能力被试，4PM得到的能力参数估计结果普遍高于3PM。

图2　不同被试四参数Logistic模型与三参数Logistic模型能力参数估计值

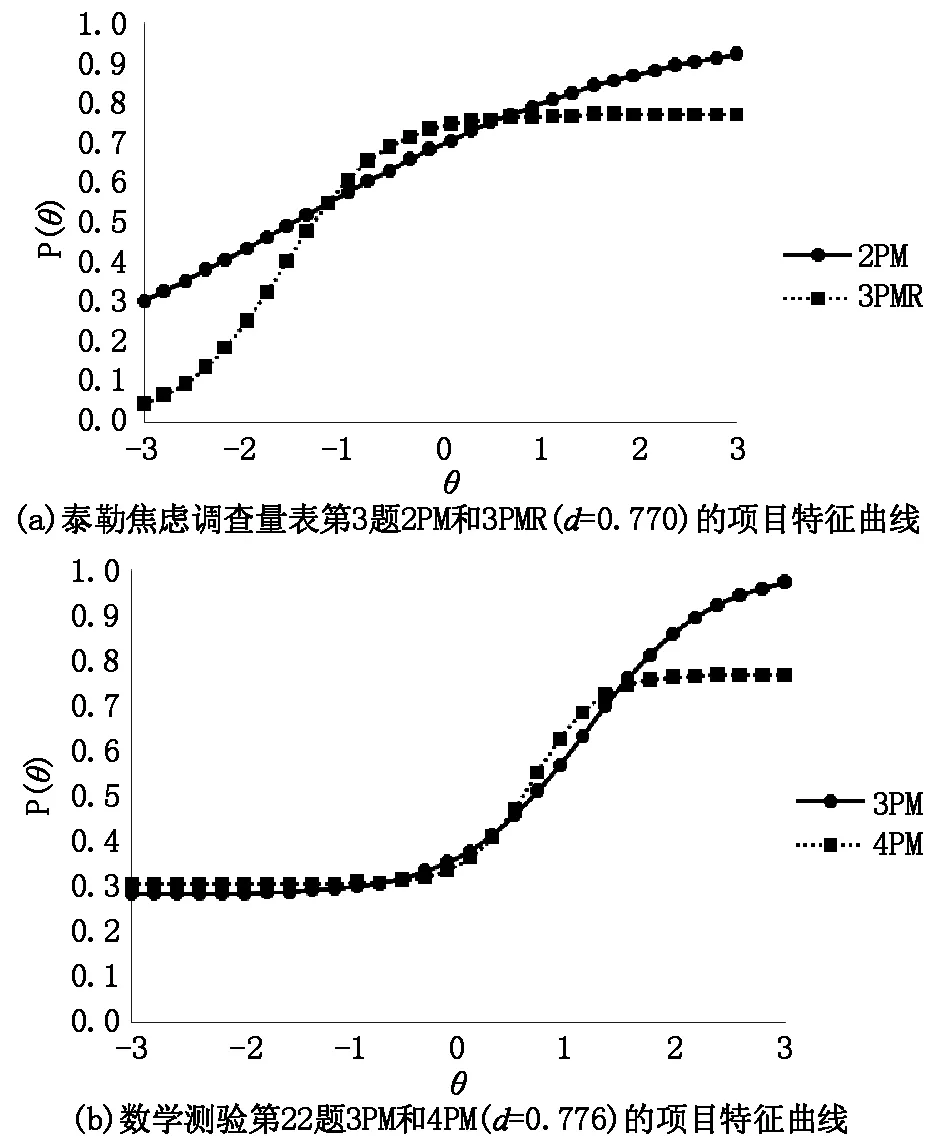
图3　四参数Logistic模型与传统模型项目特征曲线

3.3　项目特征曲线分析

为了进一步证明上渐近线参数非1现象的存在，在泰勒焦虑调查量表和数学测验中分别选取了d参数显著小于1的一道题目，绘制不同模型的项目特征曲线(ICC)，如图3所示。

从图中可以看出，实际测验中确实存在上渐近线参数显著小于1的题目。对于这些题目，传统模型的上渐近线为1，高能力被试答对题目的概率接近1；而四参数Logistic模型的上渐近线小于1，高能力被试答对题目的概率显著小于1。

4　讨论

4.1　四参数Logistic模型的必要性

研究以实际数据为例，展示了四参数Logistic模型如何用于分析心理测验和成就测验，并与传统模型的拟合性和参数估计结果比较，总结出四参数Logistic模型的必要性。

4.1.1四参数Logistic模型对心理测验的必要性

早期关于四参数Logistic模型的文章中，多认为该模型更适用于心理和人格测验。这是由于三个原因造成的：一是心理测验题目存在着极端性，即某些题目有基础的选择率，会存在非0下渐近线现象和非1 上渐近线现象。例如，有调查显示，有自杀倾向的青少年比例小于0.50，那么在青少年的抑郁量表中，即使有重度抑郁的人，也不一定有自杀倾向。二是心理测验项目上存在“非对称的项目特征模糊性(non-symmetric item ambiguity)”，即人格测验在人格特征维度上的一端测量可以模糊，而在人格特征维度的另一端的测量要求精确。这时需要c或d参数来反映，以得到更精确的测量(简小珠，焦璨，彭春妹，2010)。三是相比于成就测验，心理测验所关注的峰值具有较强的灵活性。在大多数心理测验中，量尺的两端都具有一定的意义。如果由于解释分数的需要，将原有的量表方向反向，那么原本需要猜测参数的题目反向后需要睡眠参数。因此，在很多研究中都证明了在心理测验中，四参数Logistic模型的适用性(Waller & Reise，2010)。

四参数Logistic模型用于泰勒焦虑调查量表也具有较大的优势。第一，从模型拟合指标来看，考虑了睡眠参数的模型其AIC拟合指标结果最好。第二，从参数估计结果来看，考虑了d参数的模型与传统模型在区分度、能力参数估计值上具有一定的差异，传统模型会低估一些题目的区分度参数，低估高能力被试的能力参数。第三，从具体的题目参数估计结果来看，确实存在d参数显著小于1的题目。例如第15题，题目为“我的手脚经常是暖的。(My hands and feet are usually warm)”，该题为反向计分，d参数显著小于1(d=0.58，se=0.007)。测验设计者假设，越焦虑的人，他们的手脚就越不会暖。但是实际数据证明，在所有被试中，有接近半数选择了“是”，这可能是因为手脚温暖也存在基础选择率，即在所有人群中，本来就有很大比例的人手脚是暖的。因此，对于这类题目，加入d参数进行数据拟合就非常必要。

4.1.2四参数Logistic模型对成就测验的必要性

研究者曾经对ETS所收集的成就测验的数据(如SAT的语言部分、SAT的数学部分、GRE的语言部分等)采用四参数Logistic模型进行拟合，结果证明，四参数Logistic模型没有提高测验的似然值，得到的能力估计结果也没有显著的差异，并且计算复杂，因此没有较大的实践价值(Barton & Lord，1981)。

但是随着ETS让参加测试的学生免费重考事件的出现(Carlson，2000)，许多研究者开始关注在CAT中被试能力被严重低估而导致不可信的问题(Rulison & Loken，2009)。

在传统的纸笔测验中，也可能存在由于睡眠现象而导致被试能力低估的问题。这时，也可以应用四参数Logistic模型来对能力估计值进行矫正，得到更为准确的测量结果。对于数学测验和构造的负偏态数学测验，四参数Logistic模型在各拟合指标上均优于传统模型；在区分度参数估计结果上与传统模型有较大的差异，并且当低难度题目比例相对较大时，这种差异更为明显；高能力被试的能力估计结果也普遍高于传统模型。另外，在具体的题目参数估计结果上，也有一些题目的d参数估计值显著小于1。对比原始数学测验和构造的负偏态数学测验的估计结果可以发现，对于构造的负偏态数学测验，四参数Logistic模型和传统模型在区分度参数估计结果上的差异更大；而在两种分布下，不同模型在能力参数估计结果上的差异没有显著区别。研究假设在负偏态的分布中，由于高能力的被试比例较大，因此四参数Logistic模型的优势应更明显。但是实际结果并没有证明这一假设。这可能是由于一方面，构造的负偏态分布是基于测验的原始分得到的，这种经典测量理论下的原始分对被试能力水平的描述本来就存在较大的误差；另一方面，所构造的数据偏度为-0.199，偏度较小，可能尚未达到使得四参数Logistic模型优势得以突显的程度。因此，未来的研究可以考虑使用模拟的方法，构造不同分布的数据，系统地考察四参数Logistic模型与传统模型的差异。

综上，成就测验实际数据分析结果证明，对于研究所选用的成就测验，有必要使用四参数Logistic模型进行拟合。

4.2　四参数Logistic模型的使用建议

传统模型是四参数Logistic模型的特例，在实际中，是否需要选择四参数Logistic模型进行数据拟合可以考虑以下几个方面的问题：

一是测验的类型。对于心理测验，由于被试无意识的社会期望反应和掩饰防御反应等等，被试作答存在着非0下渐近线现象和非1 上渐近线现象，会影响测验结果的准确性(简小珠，焦璨，彭春妹，2010)。因此，建议使用四参数Logistic模型进行参数估计。对于成就测验，有条件的情况下，可以在三参数Logistic模型的基础上，使用四参数Logistic模型的估计结果作为验证与补充，纠正高能力被试答错容易试题时的能力低估现象。另外，如果测验中简单题目的比例较高，使用四参数Logistic模型可能会得到较为准确的结果。

二是测验的目的。对于某些成就测验而言，准确地估计被试的能力水平非常重要。例如在一些高利害的测验(如高考)中，每个考生的能力估计结果都会造成直接和重要的后果，其准确性就显得尤为重要。如果由于睡眠现象的存在，低估了高能力考生的能力值，就会对高能力人才的发展产生诸多不利的影响。另外，对于安置性测验(placement test)，考生能力的估计结果直接影响到学生的分班、分级，如果由于使用了不合适的模型进行拟合而低估了高能力考生的能力值，会导致分班结果的偏差，进而影响到高能力学生后续阶段的学习。因此，在这些成就测验中，考虑到测验的目的，可以使用四参数Logistic模型，保证高能力被试能力估计结果的准确性。

三是运算的复杂程度。早期使用四参数Logistic模型的主要障碍在于计算的复杂性和费时，随着估计方法和计算机性能的发展，最新的IRT 软件WINSTEPS(Linacre，2009)包含了四参数logistic 模型的项目参数估计模块，R语言中的sirt软件包也具有拟合四参数Logistic模型的功能。这些软件的发展使得在选择四参数Logistic模型时，运算的复杂程度已不是制约模型应用的主要因素，为其广泛应用奠定了基础。

4.3　有待进一步研究的问题

研究所涉及的实际数据，均为0/1计分。今后，可以将四参数Logistic模型推广到多级评分的题目，甚至混合题型的测验中。

其次，四参数Logistic模型的等值也是值得深入研究的问题。可以探索使用该模型是否能够显著提高高能力群体被试能力等值结果的准确性。

最后，随着多维项目反应理论越来越受到关注，如何将四参数Logistic模型推广至多维情境中，也需要更多的研究者付诸努力。

5　结论

在实际测验中，确实存在睡眠现象。四参数Logistic模型能够显著提高模型对心理测验和成就测验数据的拟合性，纠正区分度参数低估和高能力被试答错容易试题时的能力低估现象。因此，在实际测验的数据分析中，应当根据具体情况，必要时使用四参数Logistic模型替代传统模型，对参数估计结果进行验证与补充，以提高测量结果的准确性。