某型直升机RCS的仿真计算与分析

杨继云

(中国人民解放军92941部队，辽宁 葫芦岛,125001)

0　引　言

RCS(雷达散射截面积,Radar-Cross Section)是直升机散射特性的一个重要参数，雷达就是根据目标对其入射波的有效散射截面积来发现目标的。通过对直升机RCS的研究，可以为今后的设计、生产提供一定的指导，因此计算它的RCS有重要意义。

目前，直升机的雷达目标特性计算方法主要有全尺寸测量、缩比模型测量、动态测量、数学仿真计算等。本文采用物理光学法的Stratton-Chu积分方程计算直升机各面元的散射场，采用等效电流法计算直升机各边缘的绕射场，再将直升机各面元的散射场和直升机边缘的绕射场进行矢量叠加，获得直升机总的RCS。然后将理论计算结果与动态测量试验结果进行对比分析，验证该仿真计算方法的有效性。

1　理论方法

1.1　表面散射场的计算

物理光学法的出发点是Stratton-Chu积分方程，根据Stratton-Chu积分公式，可以得出物体表面外任一点P的散射场强。

Es=∮s[jωμ(n×HT)ψ+(n×ET)×ψ+
(n·ET)ψ]ds

(1)

Hs=∮s[-jωε(n×ET)ψ+(n×ET)×ψ+
(n·ET)ψ]ds

(2)

式中：ET，HT分别表示总的电场和总的磁场；n为物体表面的单位法向量；s为散射体表面；ψ为自由空间格林函数。为了简化积分运算，把积分方程化为定积分方程，将目标表面离散为一定数量的多边形面元，计算各面元的散射，叠加得到整个目标表面的散射场。对于任意导体曲面，化简远场积分得到的散射电场强度为

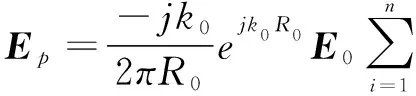
(3)

令IP=∬sie-2jk0zdxdy，si为曲面片，计算出IP值，就能求出整个目标的表面散射场。将目标表面离散为若干个三角形面元，它们的参数为提取的目标“面元-边缘”网格数据中的顶点和面元数组。一般认为曲面片上任意一点到该替代平面的距离小于λ/16时就能满足计算精度的要求，这样就把IP的面积分转化为线积分，得到Ep的解析表达式，即求出了各面元的散射电场。

1.2　边缘绕射场的计算

在远离镜面反射方向上，物理光学计算的场并不精确，而且随着散射方向偏离而变化。因此，在复杂目标散射场计算中，必须考虑由边缘引起的绕射场，使理论计算具有更强的适应性。

等效电磁流法的根据是：任何有限电磁流分布的远区绕射场通过一个辐射积分来求和时，将得到一个有限结果，所以该方法假设在边缘各点处存在线电流Ie和线磁流Im，并以远场辐射积分的形式对它们求和来表示绕射场，如式(4)所示。

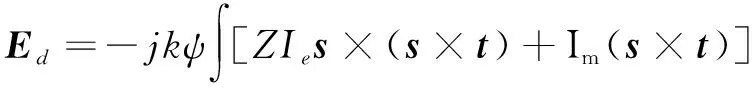
(4)

式中：ψ为自由空间的Green函数；k为入射波的波数；t为沿该边缘回路方向的单位矢量。各参数如图1所示。

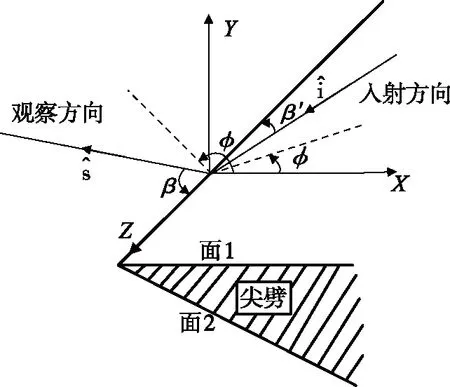
图1　边缘绕射的几何结构Fig. 1　Geometry of edge diffraction

将表面场积分与直尖劈的解析解相联系，可求得不含物理光学项的等效电流Ie为

(5)

(6)

将等效线电流Ie和线磁流Im代入式(4)，便可求出边缘绕射场Ed为

(7)

式中：C为边缘，但求解Ed的积分仍复杂困难。为了工程实用计算，对边缘进行简化处理：将边缘划分为若干小段，每一小段都用直线来模拟，它们的参数是提取的目标“面元-边缘”网格数据中的顶点和边缘数组，分别对离散的每一小直线段边缘进行计算，然后进行矢量叠加得到边缘绕射场。

1.3　遮挡处理

在采用“面元边缘法”计算目标RCS前，必须判别所处理的面元和边缘是否被遮挡。当雷达波照射到目标时，表面被分为两个部分：照射区和阴影区。处于阴影区或被遮挡的面元和边缘对后向散射场没有贡献，计算中应当去除。应用计算机图形学中消隐方法来判断、处理遮挡问题。具体方法如下：

1) 首先判断目标表面是否处于照射区(设入射波法矢为i，面元外法矢为n)，如果i·n≥0，表面处于阴影区；如果i·n<0，表面处于照射区。

2) 将目标上所有处于照射区的面元和边缘投影到垂直于雷达波入射方向的平面上，这样就将复杂目标的表面投影到了二维平面上。

3) 在投影平面上计算照射区各面元的几何重心，并在入射方向上按深度进行排序，从而确定目标表面的相交区域和重叠的顺序。

4) 只有最上面一层的面元和边缘才对后向散射场有贡献。

1.4　目标总散射场

总散射场=面元散射场+边缘绕射场，表示为

(8)

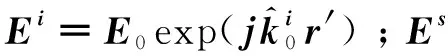
2　仿真计算

2.1　目标建模

1) 根据目标外形尺寸、几何参数，进行计算机辅助建模，详见表1。

2) 划分电磁计算网格。机身的电磁计算网格用一系列拓扑结构的面元和棱边来描述。面元足够小，就能精确地描述目标的外形。这样便将复杂的曲面积分转化为各平面积分的代数和，从而实现RCS计算方法和程序中对复杂积分方程的求解。由上述方法获得的电磁计算网格，见图2。

3) 通过转换程序，构造符合RCS计算程序的拓扑结构并进行解算。

4) 确定仿真试验因素及水平。确定仿真计算频点为9.5 GHz，极化方式为垂直极化和水平极化。因条件限制，本文关于某型直升机RCS的仿真计算都是基于金属材质的基础上进行的。

表1　某型直升机的基本参数Tab. 1　Basic parameters of a helicopter

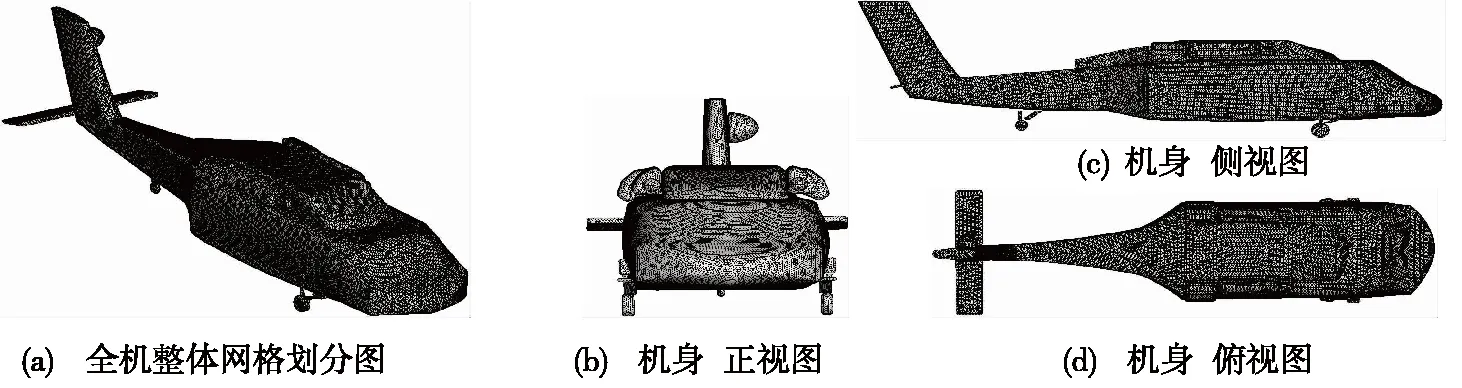
图2　某型直升机电磁计算网格划分图Fig. 2　Electromagnetic calculation grid division diagram of a helicopter

2.2　某型直升机RCS仿真计算结果

针对某型直升机，以其机身纵轴线为0°基准，按照90°的步长将数据划分为头向Ⅰ(315°～45°)、侧向Ⅱ、Ⅳ(45°～135°、225°～315°)及背向Ⅲ(135°～225°)四个区域，获得某型直升机四个区域以及全向的RCS均值、中值及方差统计计算结果，见表2。动态分布图见图3。

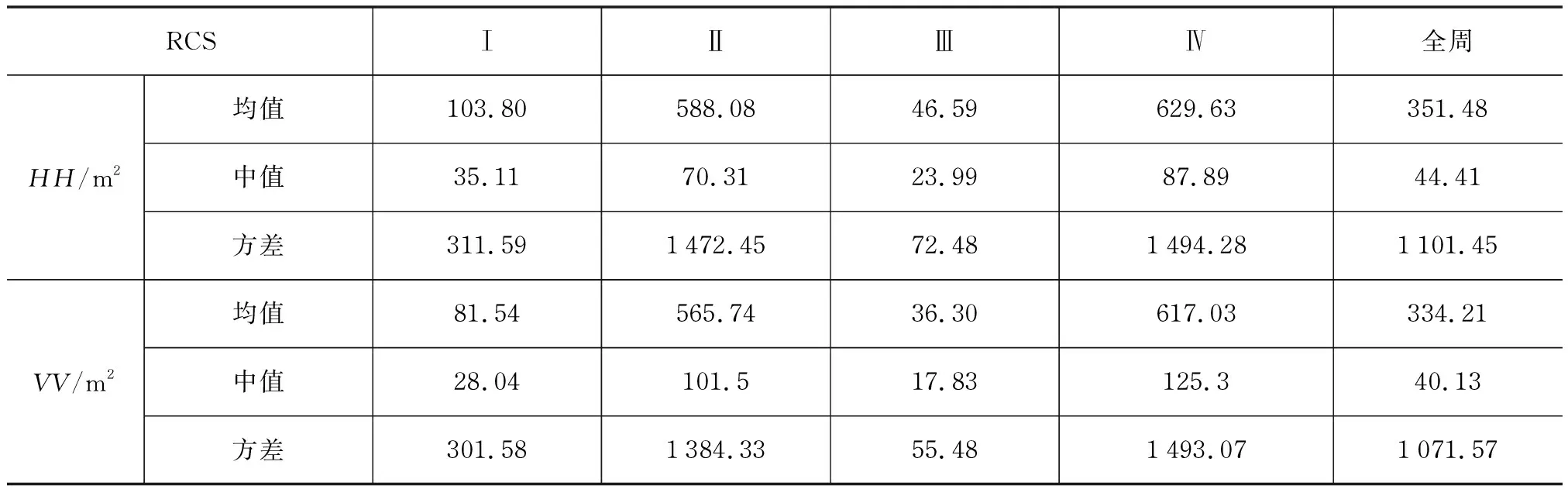
表2　某型直升机RCS仿真计算统计结果Tab. 2　Statistical results of simulation calculation for the RCS of a helicopter

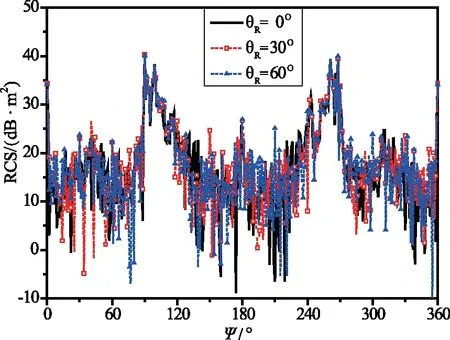
图3　某型直升机RCS动态分布曲线图Fig. 3　Dynamic distribution graph of the RCS of a helicopter

3　动态测量试验结果

动态测量试验需选择合适的测量场地并进行测量雷达的布设，分为悬停状态飞行试验和接近及远离飞行试验两种，本文选择接近及远离状态飞行试验。试验中，直升机在约200 m高度，1 000～4 000 m距离范围内往复飞行。其试验航路示意图如图4。

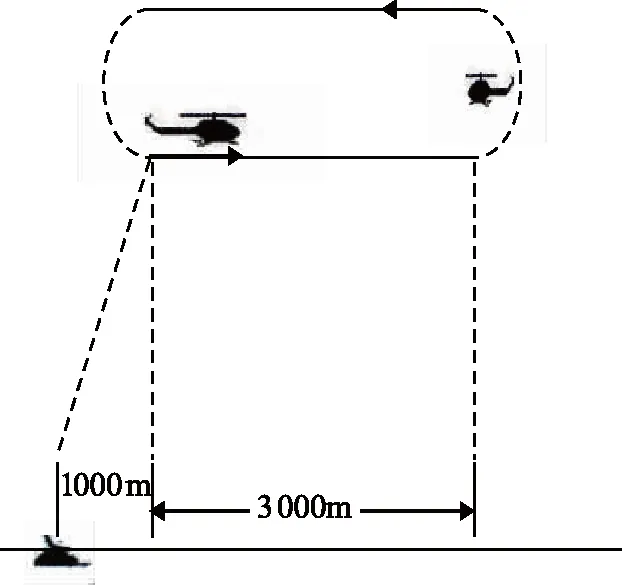
图4　某型直升机接近—远离状态下RCS测量示意图Fig. 4　Schematic diagram of measurement for the RCS of a helicopter

由于试验条件的限制，某型直升机RCS动态测量试验获得的是9.5 GHz、-20°～0°俯仰角条件下该型直升机RCS的测量值，见表3。

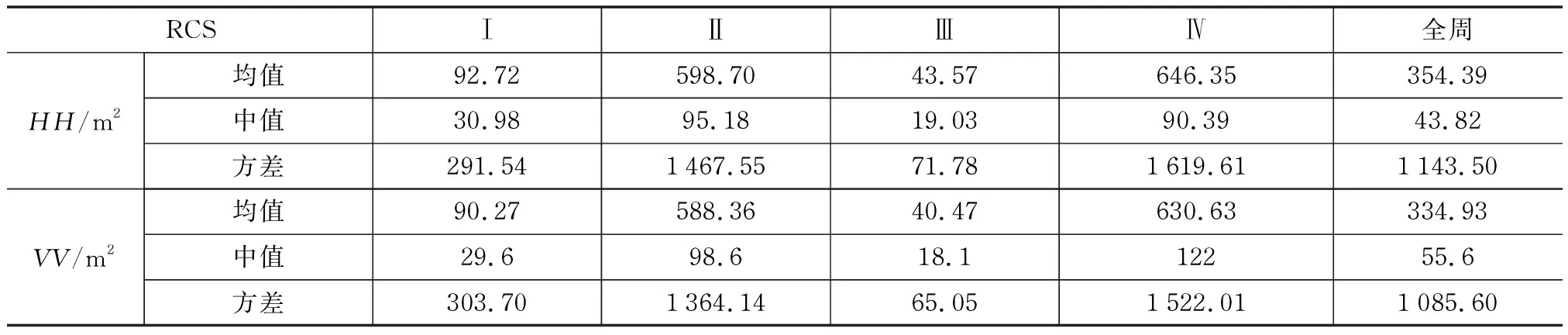
表3　某型直升机RCS动态测量统计结果Tab. 3　Statistical results of RCS dynamic measurement of a helicopter

4　对比分析

由于受到飞行姿态、大气等因素的影响，仿真计算获得的RCS分布特性与动态试验获得的RCS分布特性会有一定差别。针对该型直升机的仿真计算与动态测量试验数据进行对比分析，仍然可以看出：

1) RCS仿真计算与动态测量的均值分布特性基本相同，都是头向及背向的RCS相对较小，侧向的RCS相对较大。

2) 与仿真试验数据相比，动态测量条件下的RCS均值略大，两种情况下的方差水平基本相同，具有相同的散射特性。

5　结束语

通过对某型直升机RCS的仿真计算以及与动态测量结果的对比分析，得出结论：基于物理光学、等效电磁流法和准静态法相结合的RCS仿真计算方法，对直升机的机身和旋翼RCS特性仿真具有较高的精度和效率，能满足工程应用的要求。