矩阵分析方法在压烫工艺优选中的应用
方蕾蕾 吴巧英


摘 要:为探究矩阵分析方法对多指标压烫工艺优选的适用性,选取3种精纺全毛面料与2种黏合衬作为实验对象,设计3因素3水平正交压烫实驗,采用矩阵分析方法分析实验结果,并将其分析过程和结果与综合平衡法进行对比。研究发现,矩阵分析方法得到的结果与综合平衡法相一致;并且相较于传统的综合平衡法,矩阵分析方法具有计算简单、过程明了、结果准确的特点和优势。
关键词:矩阵分析;正交试验设计;压烫工艺;黏合衬;全毛精纺面料
中图分类号:TS941.66
文献标志码:A
文章编号:1009-265X(2018)02-0046-07
Application of Matrix Analysis Method in Pressed-ironing Process Optimization
FANG Leilei, WU Qiaoying
(School of Fashion Design and Engineering, Zhejiang Sci-Tech University, Hangzhou 310018, China)
Abstract:To explore the applicability of matrix analysis method in multi-index pressed-ironing process optimization, three kinds of worsted wool fabrics and two kinds of interlinings were selected as the test subjects to design three-factor and three-level orthogonal test. Matrix analysis was used to analyze test results. Besides, the analysis process and results were compared with overall balance method. The study finds that the results of matrix analysis method are consistent with those of overall balance method. And compared with the traditional method, the matrix analysis method has the characteristics and advantages of simpler computation, clearer analysis process and more accurate results.
Key words:matrix analysis; orthogonal experiment design; pressed-ironing process
温度、时间、压力是面料与黏衬压烫黏合的三要素,不良压烫工艺会降低黏合质量,导致黏后渗胶、洗后黏衬脱落、起泡、起皱等问题,严重影响服装外观质量。因此,基于黏合效果的压烫工艺优化选择是服装生产中十分重要的质量控制环节。由于压烫工艺优选所需考虑的因素较多,常采用正交设计方法来安排试验;又因实际生产和使用中出现的黏合问题较复杂,故黏合效果常采用剥离强度、尺寸变化率、外观质量等多个指标来评定,属于典型的多指标正交试验;对其试验结果的分析,目前常采用综合平衡法[1-2]。综合平衡法是先对各指标分别进行直观分析,得出因素的主次和优方案,再结合专业知识和经验对各指标的分析结果进行综合平衡,得到综合的优方案[3]。该方法分析计算工作量大,分析过程复杂,不利于研究对象及观察指标多的压烫工艺优选试验结果分析。因此,本文采用矩阵分析法解决多指标压烫工艺优方案选择问题。
矩阵分析法[4]是功效系数法的一种方法,它是根据多目标规划原理,对每一项评价指标确定一个满意值和不允许值,以满意值为上限,以不允许值为下限,计算各指标实现满意值的程度,并以此确定各个指标的分数,再经过加权平均进行综合从而评价被研究对象的综合状况。目前,矩阵分析法已在多个领域中得到应用,如社会科学领域中运用矩阵分析结合学生能力、品德、知识3个评价指标对高校学生质量进行综合评估[5],经济领域中经济责任审计的结果分析[6],管理领域中业绩评价[7],医学领域中治疗效果的评价[4]、地理勘测领域[8]等。基于压烫工艺试验的多指标特征,可以尝试将矩阵法用于试验结果的优选分析,降低分析难度。本文在3因素3水平压烫工艺正交试验基础上,运用矩阵法计算出不同因素及水平对试验结果影响的权重,根据权重大小确定压烫工艺最优方案以及各个因素对指标值影响的主次顺序[9-10],并与综合平衡法进行对比,验证了该方法在压烫工艺优选中的适用性。
1 试 验
试验材料:3种全毛精纺面料(江苏阳光集团),2种梭织双点黏合衬(东莞市裕纺衬布有限公司),基本参数分别见表1、表2。
主要仪器:SR-400黏合机(日本SUMMIT公司),YG034-BQ3剥离强度仪(上海瑞纺仪器有限公司),HXL8010E干洗机(意大利F.M.B.集团),T60标准光源箱(苏州天友利仪器有限公司)。
组合试样编号:按照“面料编号-黏合衬编号”,如1-2,1为面料编号,2为黏合衬编号。
测试方法:采用3因素3水平压烫工艺正交试验方案,各因素水平见表3。参照FZ/T01085—2009《热熔粘合衬剥离强力试验方法》测试组合试样干洗后剥离强度及离散系数[11]。参照FZ/T 01083—2009《热熔粘合衬干洗后的外观及尺寸变化试验方法》测试干洗后经、纬向尺寸变化率及外观质量等级。其中外观质量等级分5级,5级表示外观完全平整。
2 试验结果及观察指标选取
试验结果如表4所示,全毛精纺面料与梭织衬黏合试样的干洗后剥离强度与离散系数的极小值与极大值差量分别为11.23 N和32.85%,不同组合试样在不同工艺参数条件下测试结果差异较大。黏合试样干洗后经、纬向尺寸变化率均值分别为-0.72%、-0.29%,经向尺寸变化率明显高于纬向。干洗后外观评价高于4.0级、纬向尺寸变化率绝对值低于0.53%,两项指标的标准差均较小,可见干洗后试样具有良好的外观平整度及纬向尺寸稳定性,试样间质量差异小,表明此两项指标受本试验设计的压烫工艺水平的影响较小,无需用作工艺优选观察指标。因此,将用于压烫工艺优选分析的观察指标为3个:干洗后剥离强度、离散系数以及经向尺寸变化率。
3 矩阵分析用于优选压烫工艺
通过直观分析,得到温度、压力、时间3个因素对各指标的影响程度,是矩阵分析法与综合平衡法的第一步。在此基础上,基于矩阵分析的压烫工艺优选,将通过加权平均进行综合评价,根据得到的权重大小确定压烫工艺最优方案以及各个因素对指标值影响的主次顺序。以组合试样1-1为例,直观分析结果见表5,优选压烫工艺的矩阵分析过程根据矩阵分析的定义进行,详见3.1~3.5。
3.1 建立数据结构模型
首先根据正交试验设计的数据结构建立一个三层结构模型,试验观察指标列为第一层,各因素列为第二层,各水平列为第三层。根据本文正交试验设计,构建的数据结构如表6所示。
3.2 建立试验观察指标层矩阵M
如果正交试验中设有n个因素(X1,X2,…,Xn),每个因素有m个水平,用kij表示因素Xi第j个水平上的試验指标的平均值。若试验结果的观察指标越大表示越好,则令Kij=kij;若试验结果的观察指标越小表示越好,则令Kij=1/kij;建立式(1)试验观察指标矩阵M。
本试验观察指标中,干洗后剥离强度为越大越好,离散系数为越小越好。而经向尺寸变化率存在正负值,分别对应干洗后尺寸收缩或伸长,该指标为越接近0越好,为方便分析,对经向尺寸变化率取绝对值,该值为越小越好。根据式(1),分别建立3个观测指标的指标层矩阵干洗后剥离强度M1、离散系数M2、经向尺寸变化率M3。
3.3 建立因素层矩阵T
令ti=1/∑mj=1Kij,建立因素层矩阵T,如式(2)。根据定义,分别计算得到干洗后剥离强度、离散系数、经向尺寸变化率的因素层矩阵T1、T2、T3。
3.4 建立水平层矩阵S
Ri为正交试验中因素Xi的极差,令Si=Ri/∑ni=1Ri,建立(3)式矩阵。矩阵中S1为R1/∑ni=1Ri,表示因素X1的极差占所有因素的极差总和的比值。
因此,根据定义可分别得到剥离强度、离散系数和经向尺寸变化率的水平层矩阵S1、S2、S3,如式(3)所示。
3.5 计算权矩阵ω
计算影响试验指标的权矩阵为ω=MTS。
ωT=[ω1ω2…ωm](4)
式(4)矩阵中ω1=K11T1S1。其中,S1为因素X1的极差在所有因素的极差总和中的占比;K11T1为K11/∑nj=1K1j,表示因素X1的第一个水平的指标值占因素X1所有水平的指标值总和的比值;二者乘积即为ω1,其反映了因素X1的第一个水平对试验指标的影响程度和极差的大小,即该因素水平对试验指标影响的权重大小。同理可计算出其他的因素和水平的权重,根据权重能够得出最优方案以及影响因素的主次顺序。
根据上述计算方法,可分别计算剥离强度、离散系数、经向尺寸变化率的权矩阵ω1、ω2和ω3。
由计算结果可知,温度A 3个水平对试验结果的影响权重分别为:A1=0.075、A2=0.071、A3=0.074,A1的权重最大;同理,压力B中B2权重最大为0.124;时间C中C1权重最大为0.200。因此,可确定1#面料与1#黏衬的最佳压烫工艺为A1B2C1,即温度为135 ℃、压力为2.5 kg、时间为12 s。再比较A1、B2、C1权重值,可以快速得出各个因素对评价指标影响的主次顺序为C>B>A,即黏合时间对黏合效果的影响最大,其次是黏合压力,最后是黏合温度。
同理可计算得到其他组合试样的最佳工艺组合,见表7。
4 综合平衡法对比分析
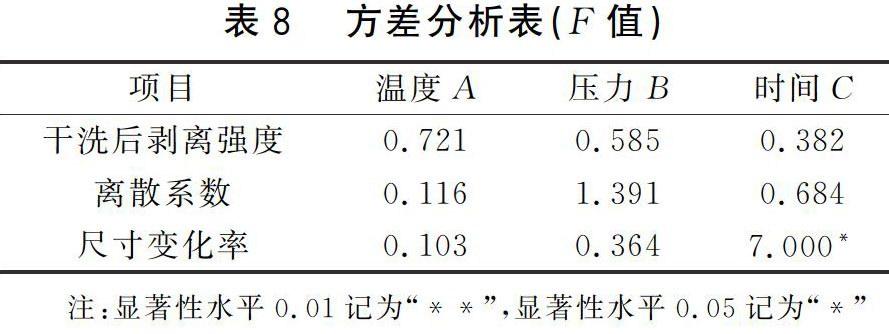
综合平衡法是目前在压烫工艺研究中使用最多、最广泛的分析方法。作为比较,运用综合平衡法对试验结果进行分析。同样以1-1为例,直观分析结果见表5;方差分析结果见表8;以因素水平为横坐标,试验指标平均值为纵坐标,绘制因素与指标的关系图(因素-指标图),图1为干洗后剥离强度下的因素-指标图。
由表5可知,仅考虑干洗后剥离强度,最优工艺组合为A1B2C2;仅考虑离散系数,最优工艺组合为A1B2C1;仅考虑尺寸变化率,最优工艺组合为A3B1C1。在3个评价指标下的最佳工艺组合不一致,则需通过综合平衡法[3]确定温度A、压力B、时间C的水平,分析如下:
温度A:由表8方差分析可知,温度水平对干洗后剥离强度、离散系数、尺寸变化率均没有显著影响。其中根据F值可知,温度对尺寸变化率的影响最小,剥离强度和离散系数下A1为最佳水平,由图1可知,3个指标在A1水平下均较良好。因此,温度水平选择A1比较合适。
压力B:压力水平对3个指标均没有显著影响,B1、B2均可接受。由F值可知,压力对尺寸变化率的影响最小。剥离强度和离散系数下B2为最佳水平,并且由表5可知,各压力水平下的尺寸变化率的极差R为0.32,极差较小。因此,压力水平可选B2。
时间C:由表8方差分析可知,时间水平对尺寸变化率有显著影响,表示不同时间水平下的尺寸变化率差异十分明显,因此首先考虑尺寸变化率,尺寸变化率下C1为最佳水平,因此时间水平选择C1。
如表8所示,时间水平对尺寸变化率有显著影响,温度水平、压力水平对指标均没有显著影响。进一步对比F值可知,时间水平对各指标的影响大于温度水平。因此综合各因素对3个观察指标的影响程度可得,因素影响的主次顺序为C>B>A。
综上所述,1#面料与1#黏合衬黏合的最佳工艺为A1B2C1,因素影响的主次顺序为C>B>A。其结果与矩阵分析结果相一致。同理可得到其他组合试样的最佳压烫工艺结果见表9。
对比矩阵分析法与综合平衡法的最佳工艺分析结果,分别见表7、表9,两种方法分析结果具有较好的一致性。根据因素主次顺序可以看到,全毛精纺面料与梭织黏合衬黏合时,对黏合效果影响最大的为时间因素,其次为温度因素,压力因素的影响则相对较小。
另比较两者的分析过程,如文献所述,综合平衡法计算量大且分析过程较复杂,需结合直观分析、极差分析、因素-指标图进行综合比较分析才可得到最优组合。当评价指标较多时,综合平衡法的运算量增大,综合比较分析的情况更为复杂。而矩阵分析方法的分析过程相对较为简单明了,通过计算权矩阵,可直接得到各因素的优水平、各水平的极差以及因素主次顺序,并且结果较准确。在矩阵分析法的实际运用中,可根据矩阵分析定义在计算机中编写计算公式,直接将数据代入后,计算机即可自动运算,并快速准确地输出结果。
5 结 论
a)全毛精纺面料与双点梭织衬黏合后,压烫工艺参数对于其干洗后剥离强度、离散系数及经向尺寸变化率的影响较大,对外观平整度与纬向尺寸变化率的影响较小。
b)压烫工艺参数中,时间与温度是影响干洗后黏合效果的关键因素,压力因素的影响较小。
c)分别运用矩阵分析法、综合平衡法,得到全毛精纺面料与梭织黏衬组合试样的最佳压烫工艺以及各因素影响的主次顺序,两种方法的分析结果具有较好的一致性。
d)运用矩阵分析法来解决面料与黏合衬压烫工艺的优选是一个新的尝试。矩阵分析方法计算简单,分析过程严谨,并且计算结果具有说服力和准确性,适用于解决多指标压烫工艺优方案选择问题。
参考文献:
[1] 劉雪婷,徐军,赵竟钰.西服面料与粘合衬压烫工艺参数的优化选择[J].西安工程大学学报,2012,26(2):174-178.
[2] 张金瑞,赵丽丽,薛美君,等.轻薄毛纺面料与粘合衬压烫工艺参数的优化选择[J].国际纺织导报,2005(1):75-79.
[3] 李云雁,胡传英.试验设计与数据处理[M].北京:化学工业出版社,2008:132-139.
[4] 沈舒文,郭丽媛,宇文亚,等.基于矩阵分析法的辩证论治效果评价方法探讨[J].中华中医药学刊,2011,29(9):1935-1937.
[5] 郭竹梅.矩阵分析法在高校学生质量评价中的应用[J].河北北方学院学报(自然科学版),2011,27(4):14-17.
[6] 赵岩.矩阵分析法在经济责任审计结果分析中的应用[J].中国内部审计,2014(8):77-79.
[7] 陆庆春,田华.矩阵分析方法在企业业绩评价中的应用[J].水利经济,2007,25(1):37-41.
[8] WEI X L,LI X R,WANG J H,et.al. Application of matrix analysis in multiple index Orthogonal TestDesign[J]. Advanced Materials Research, 2012,516-517:558-562.
[9] 魏效玲,薛冰军,赵强.基于正交试验设计的多指标优化方法研究[J].河北工程大学学报(自然科学版),2010,27(3):95-99.
[10] 周玉珠.正交试验设计的矩阵分析方法[J].数学的实践与认识,2009,39(2):202-207.
[11] 骆顺华.剥离强度测试数据分析的理论研究[J].北京纺织,2005,26(2):39-40.

