基于NSGA-II的被动浮标布阵优化算法

曾浩袁延艺李彦宁

（1.海军研究院,北京,100161;2.北京中科海讯数字科技股份有限公司,北京,100095）

被动声呐浮标是应召反潜的主要装备，是一种布设方便、搜索范围大、搜索效率高的搜潜方法。然而，反潜机每次携带的浮标数量有限，且水下目标的航向航速等变化对目标的搜索具有很大影响[1-4]，因此需要对阵形、阵元数量等因素进行优化选择，提高浮标阵的效能。2008年，周旭等[5]提出了基于遗传算法（Genetic Algorithm，GA）的被动浮标布阵方法，成功证明了在复杂水声环境中，GA可有效优化浮标阵形，并提高其探测效能，但对存在约束条件的复杂情况处理能力不强。文献[6]结合反潜机本身机动能力，建立了布放包围浮标阵应召搜潜模型，并进行仿真分析。布放包围阵、直线阵能有效提高阵形的探测概率。

为了提升浮标阵探测和定位的能力，本文将快速非支配排序遗传算法（Non-Dominated Sorted Genetic Algorithm-II，NSGA-II）应用到浮标优化布阵中，结合浮标应召搜潜战术，将浮标阵的累积探测概率(Cumulative Detection Probability，CDP)作为优化目标，对采用被动全向浮标反潜的阵形进行优化，提高浮标的布阵效能。

1 应召搜索区模型

在应召搜潜时由于受到时间延误、目标潜艇运动等因素的影响，目标可能存在的区域范围较大，因而需要建立应召搜索区模型来确定应召搜索区的大小[7]。当已知道潜艇的大概位置但无法判断潜艇的航向时，一般以布设圆形阵的方式建立搜索区域模型。圆形搜索区的范围由敌潜艇位置的初始散布、搜索区的远界和近界确定，在此仅对远界条件进行分析。通常发现敌潜艇的兵力所报告的潜艇的位置会存在一定误差，如图1所示。中心部分斜线状阴影部分为敌潜艇位置的初始散布区域，用R分布表示，假设敌潜艇的位置误差为σ,依据概率统计理论中的3σ原则[8]，得到敌潜艇的散布半径R分布= 3σ。外围斜线阴影部分即为圆形搜索区外围的范围，由搜索区远界的半径R远界确定。

图1 圆形搜索区范围示意图

搜索区的远界主要由R分布、延迟时间t延迟、在搜索区内布放浮标所需时间t布放和敌潜艇可能的最大航速v潜最大决定。

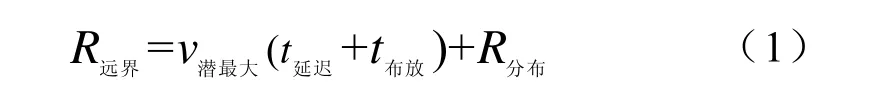
式（1）中，t延迟是从发现敌潜艇至反潜直升机开始搜索时的时间间隔，由于采用先布设后监听的方法，因此t布放很大程度上取决于组成声呐浮标阵的声呐浮标的数量n浮声。

对于圆形阵一般沿圆形搜索区远界的内沿布设声呐浮标，因此当布设单枚浮标所需要的时间t单枚和参与布设的反潜直升机的数量n直升机一定时，所需浮标数量n浮声主要取决于R远界、声呐浮标有效探测距离D浮声和相邻声呐浮标之间的间距d浮声，当浮标间的连线能够覆盖所有的探测区域，此时的浮标间距与浮标的个数的关系[5]：

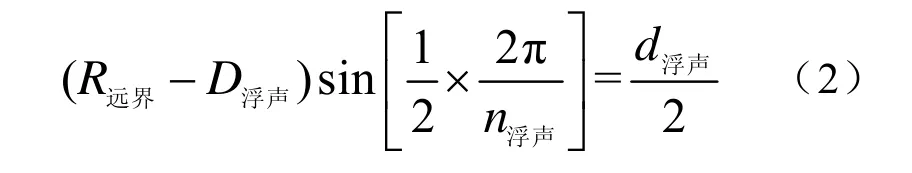
对式（2）作变换得到浮标个数：

由以上分析可知t布放是R远界的函数，而R远界又是t布放的函数，因此两者是一种嵌套关系。为得到最终结果，在计算t布放时，先使用式（4）中不考虑t布放的Rc远界来替代R远界，通过（1）式与（3）式反复迭代，逐渐逼近真实结果[5]。

以上通过布放圆形包围阵的方式得到了应召搜潜的搜潜区域。但潜艇自身的机动对单一的圆形阵搜索效率有很大影响，如潜艇沉入海底不做机动，单一圆形阵就很难发现。此时需要补投几枚浮标才能发现目标，搜潜效率较低[9]。因此在此搜潜区域模型的基础上，考虑在搜潜区域、浮标数量、布阵时间、浮标探测距离和相邻浮标间距的约束下対阵形进行优化，实现对目标的探测以提高搜潜效率。

2 浮标布阵多目标函数模型

2.1 目标函数的建立

本文考虑对浮标阵形的目标函数进行优化。以搜潜所需时间以及阵元间距与浮标数量作为约束条件，在有限监听时间内阵形的CDP为：

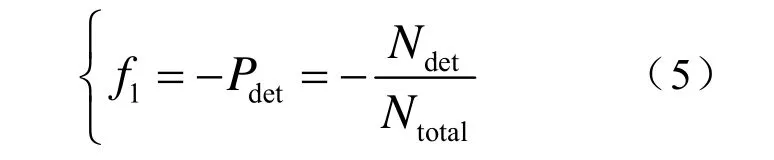
式（5）是对浮标阵在有效监听时间内发现潜艇概率的描述。由文献[10]中对CDP的推导可知，在[T1,T2]时间段内浮标阵的CDP与监听时间、目标的速度、航向以及浮标阵的搜索密度有关，而搜索密度是由浮标阵对整个搜索区域的覆盖程度决定的。由于实际过程中探测目标的计算很复杂，因此本文采用了简单的定距准则，即如果目标处于浮标的有效探测范围内，则探测概率为 1，否则为 0[11-12]。同时为避开复杂的数学推导，本文采用蒙特卡罗方法（Montecarlo，MC）计算CDP，即在搜索时间段内仿真产生大量的目标运动轨迹，统计被搜索到的次数。

浮标阵的效能是受到阵形、阵元数量、阵元间距、目标运动特点等多方面因素影响的，且阵形优化的各个参数之间也是相互制约的。

2.2 约束条件

2.2.1 时间约束

由于反潜搜索区域是由布放圆形阵模型得出，因此时间约束主要体现为布设圆形声呐浮标阵所需要的时间，对于优化后的阵形其布放时间应控制在布放圆形阵所需时间t圆布放之内，即0＜t布放＜t圆布放，并假设以螺旋线路线布设浮标。

2.2.2 阵元间距与浮标数量约束

在确定了浮标的探测距离后，为确保可靠探测应使声呐浮标两两之间有部分重叠，且浮标使用数量应控制在布放圆形阵所需的浮标数量内。

3 基于NSGA-II的布阵优化算法

3.1 进化算子设计

（1）染色体(The chromosome) 将染色体定义为一个长度为浮标数的序列,其中设计变量X=[x1,x2]作为一个基因（即浮标位置），则染色体可表示为：

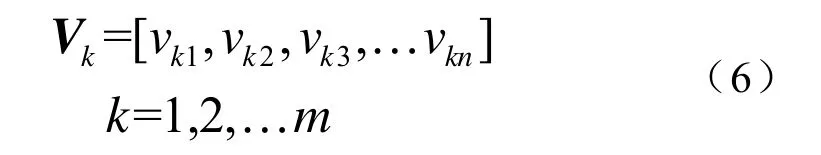
（2）初始种群(The initial population) 初始种群采用随机方式产生，即在整个搜索区域上随机布放浮标,浮标坐标由两个独立的随机数确定。

（3）交叉和变异（crossover and mutation)种群新个体的产生对种群跳出局部最优达到全局最优有重要的作用。在此，本文采取了随机交叉方式，即从父代种群中任意挑选两个个体进行多点或单点交叉。此处设置交叉算子Pr=0.8，变异算子Pm=0.1。

3.2 算法流程

NSGA-II是一种快速的非劣性排序方法，在算法中，Pareto最优解集是算法收敛后组成最优曲面的解的集合。虚拟适应度是对解的优劣性的评价，在对种群的选择操作中起重要作用。在算法选择操作中，等级低的个体优先选择，同等级下拥挤度小的个体优先选择，这样使算法的解分布均匀、收敛较快[7]。浮标布阵算法流程如下：

Step1：根据目标特性、浮标性能及搜索延迟时间等产生浮标搜索区域模型；

Step2：根据搜潜区域中浮标数量、搜索范围、布阵时间等约束条件产生N个个体并对染色体进行编码，作为初始父代种群Pt；

Step3：按比例进行交叉变异操作，形成N个个体子代种群Qt；

Step4：将父代种群Pt和子代种群Qt合并后放入进化池中；

Step5：将进化池中的2N个个体根据CDP进行快速非支配排序，得到等级F1,F2,F3...，同时对每个非支配层中的个体根据阵元距离进行拥挤度计算；

Step6：根据步骤Step4的结果选取N个个体作为新的父代种群Pt+1；

Step7：进行交叉变异操作形成N个新的个体作为子代种群Qt+1；

Step8：重复Step3至Step7 至预定代数终止。

4 仿真与分析

4.1 搜潜区域模型仿真

仿真假设：当接到命令后，反潜直升机飞往目标通报位置布放浮标阵进行应召搜潜，以接到命令时刻作为时间起点，潜艇发现位置为原点。在各向同性的海洋环境下进行搜索。假定水中声速v=1.5 km/s，采用被动全向浮标，浮标的战术作用范围是以浮标有效作用距离为半径的圆，且目标下潜深度位于浮标工作深度范围内。

输入初始条件：潜艇航速范围（Vmin,Vmax)、延迟时间、直升机速度、最大航速时浮标有效作用距离、浮标间隔。

4.2 阵形优化仿真

算法参数选择：起始种群数量100，后续种群为40，同时为了增强全局搜索能力，交叉算子取0. 8，变异算子取0.1。

潜艇运动方式：假设潜艇自被发现之时起每隔△t=0.2 h时间改变一次航速与航向，考虑到潜艇机动性，航向改变范围为[−π/3, π/3]。

由于衡量阵形效能的最优解集理论上为无限多个点且真实值不可知，因此以文献[7]中导出的相对覆盖指标作为评价算法收敛性的标准。当得到两个最优解集中的个体多数无法互相支配时，说明算法基本收敛。分别对进化代数170代、200代、230代进行10次仿真，得到三个最优解的集合U170、U200、U230，其相对覆盖指标见表1。由表中可知，当进化代数为170、200、230时得到的最优解多数无法互相支配，说明在进化代数为170代时算法已经收敛。

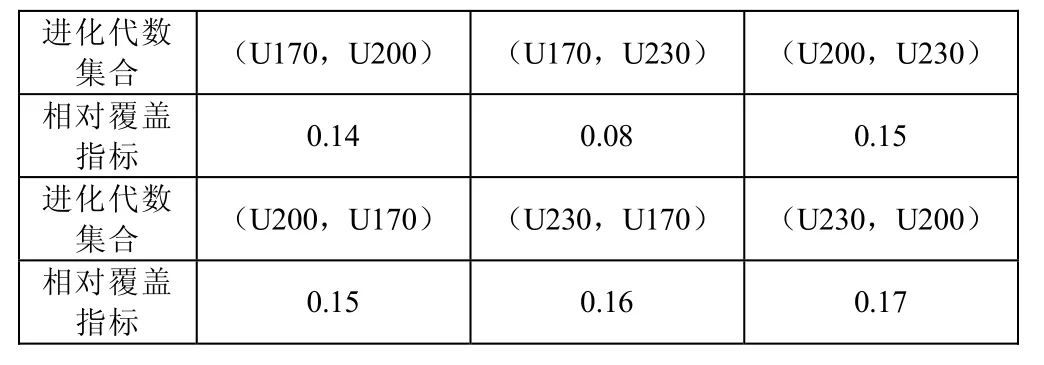
表1 相对覆盖指标

当进化代数为 200代时，得到了关于 CDP的Pareto最优解曲面图如图2所示。算法收敛后得到40个最优个体，每一个体代表一种阵形，图中每一点表示了一种阵形所能达到的CDP、定位范围的水平。从得到的最优结果中随机选择一种阵形，其阵形示意图如图3所示。

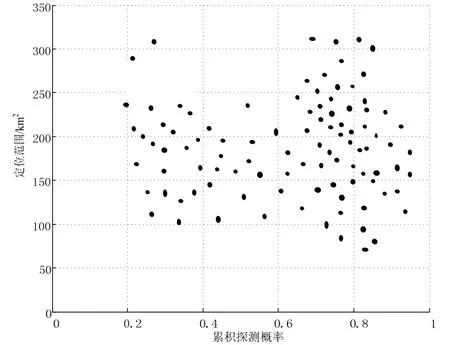
图2 CDP与定位范围分布

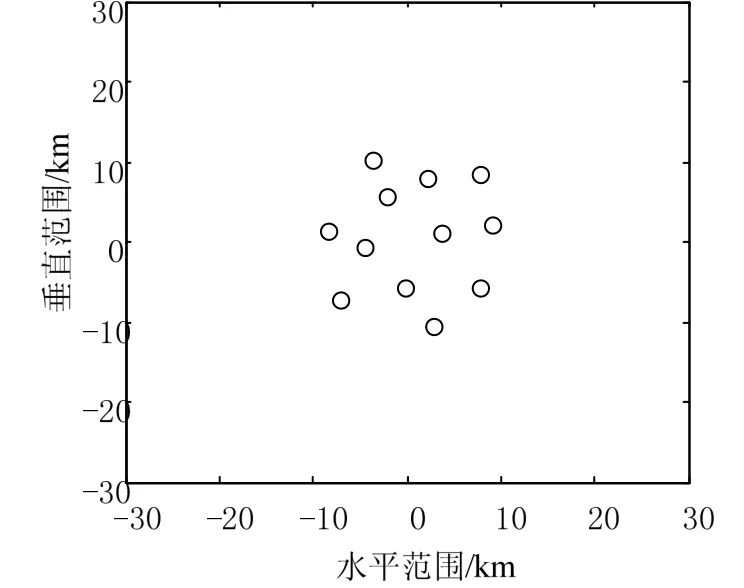
图3 NSGA-II优化后阵形

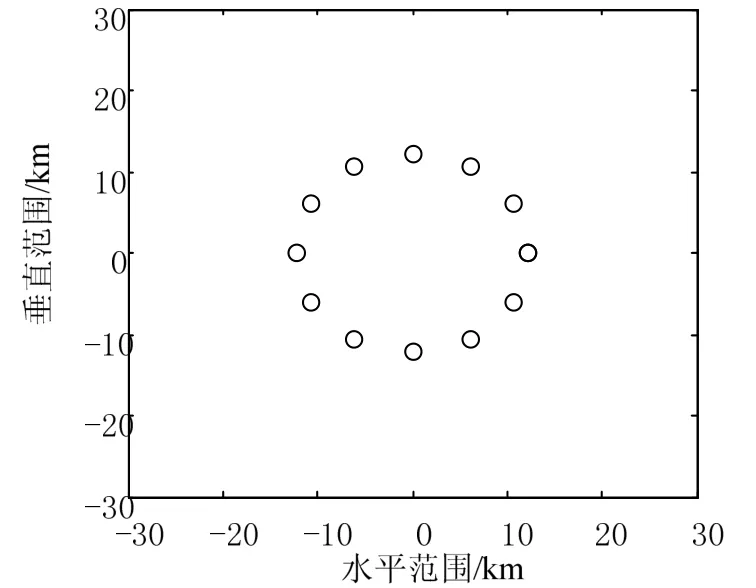
图4 标准圆形阵

在相同仿真条件下，通过将图4所示半径为12 km的标准圆形阵与优化后图3所示阵形作比较得到了不同监听时间下CDP的对比曲线，如图5所示。可以看出优化后的阵形在布阵完成后即可高效地实现对目标的探测，而单凭圆形包围阵无法实现对目标的高效探测。

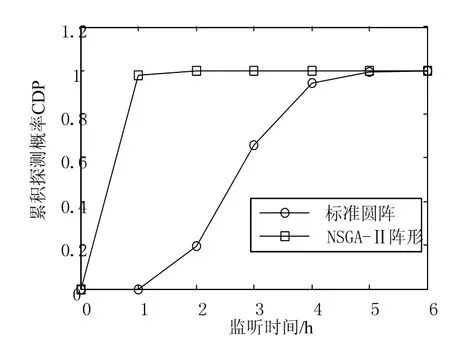
图5 NSGA-II与标准圆阵CDP对比曲线

5 结束语

本文将被动声呐浮标布阵作为一个目标优化问题，在分析搜潜区域模型的基础上，以 CDP为目标函数，通过NSGA-II算法进行优化，增加了相同浮标数量下阵形的整体效能。算法结果在目标空间上分布均匀、收敛性好。优化结果进一步表明浮标布阵的Pareto解集在布阵效能上可能存在显著差异，NSGA-II算法能为阵形决策提供更多的选择空间，为布阵效能的全局优化提供了一种新的思路和手段。