正铲挖掘机运动学分析新思路

钟伟周，陈谊超

（1.广西南南铝加工有限公司，广西南宁 530031；2.耐世特汽车系统（柳州）有限公司，广西柳州 545006）

0 引言

大型正铲挖掘广泛应用于煤炭开采，目前世界上著名的正铲液压挖掘机构是由德国O&K公司推出的[1]（图1）。该装置在水平直线挖掘时，只需要推动斗杆即可；在动臂提升时，可保证铲斗与水平面所成的角度在运动过程中不变，保障满足了平稳提升；此外，在机构整个运动过程中，提升力矩和提升力始终保持不变，因此不需要在提升过程中加大油缸的压力或直径。对于正铲液压挖掘装置的研究，国内外专家学者也做了大量工作。以特雷克斯公司的正铲挖掘机为研究对象的例子较多，如Andrew Hall[2]对公司的RH200在不同挖掘形式下系统地研究了挖掘效率及其使用寿命。Hall，A.S.和 McAree，P.R[3]则提出了一种控制算法，对铲斗的移动位置进行了有效跟踪。而Kecskemethy，A.[4]和他的学生则对该公司的RH-340利用环路转换的方法完成了运动学研究和挖掘力分析。机构的运动学分析是判断机构好坏的关键[5-6]，而对该工作装置的运动学分析还没有统一的分析方法。利用数学矢量方程，对该大型液压挖掘机进行了运动学正反解的分析，给出了该装置运动学分析的一种指导方法。

图1 正铲液压挖掘机

1 工作装置机构图及自由度分析

首先绘制出该工作装置的机构运动简图（图2）。该工作装置由大臂、上转台、动臂液压缸组件、强力三角、铲斗液压缸组件、铲斗、斗杆组成、斗杆液压缸组件和过渡连杆组成，各部件之间通过转动副连接。

依据计算自由度的公式[7]见式（1）。

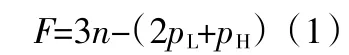
式中n——活动构件数目

pL——低副数目

pH——高副数目

将 n=12，pL=15，pH=0 代入式（1），可得该装置的自由度为3。即铲斗能实现一个转动和2个方向的移动自由度，可以满足挖掘机日常工况需求。

2 运动学正反解分析

实现机构控制主要基于机构的运动学分析。由图3可知，该工作装置由12组连杆组成的封闭运动链机构，用传统的解析方法分析比较有难度，因此，利用数学矢量方程按照模块进行分析，然后针对它们之间的几何关系实现对该工作装置的运动学分析。为便于机构的正反解分析，建立如图4所示的坐标系。

2.1 运动学正解分析

运动学正解，即在已知机构的液压缸的驱动尺寸的情况下，对末端执行器的位置和姿态完成求解。该机构主要由4个几何平面模块构成，首先对4个几何平面模块的正解进行分析，然后根据几何矢量关系，分析整个工作装置的正解。

图2 工作装置

图3 工作装置的机构示意

2.1.1 几何模块L1和L2

已知L1和L2构成了1个平面5杆2自由度的基础几何模块，液压缸s1提供驱动输入，因该机构为2自由度机构，所以需要2个输入。首先假定α1为虚输入，由余弦定理可得，见式（2）～（9）。

同理求得 α3，α4。在 L2的几何模块中，β1=360°-α4-φ5，β2=360°-α3-φ1，则

同理可以求出β3和β4，由上式可以消除虚输入α4。

2.1.2 几何模块L3

已知L3模块是一个几何平面4杆机构，其自由度为1，驱动输入由液压缸s2提供。由余弦定理可得

同理可以求出γ2和γ3。

2.1.3 几何模块L4

几何模块L4是一个6杆3自由度的平面机构，已经液压缸s3提供一个输入，而通过计算几何模块L1和L2，可推得输入θ5，通过计算几何模块L3可以得到输入θ4，从而确定该模块的3个输入，参照模块L1和L2的求解方法，可以轻松求解到L4模块。

2.1.4 整机分析

利用几何矢量表示各个部件，建立机构的封闭矢量多边形方程，建立直角坐标系（图4）。液压缸的驱动尺寸s1，s2，s3及各构件的长度已知，假设 x轴与 OF，FG，GH，HK，KN，GJ和 JK 的夹角分别为 φ1，φ2，φ3，φ4，φ5，φ6和 φ7，则有式（11）～（15）。

由以上各式可求得末端执行器的位置和姿态。

2.2 运动学反解分析

已知末端执行器的位置和姿态如式所示，求得该位置和姿态下的3个液压缸的驱动尺寸，即为位置反解。过程见式（16）和（17）。

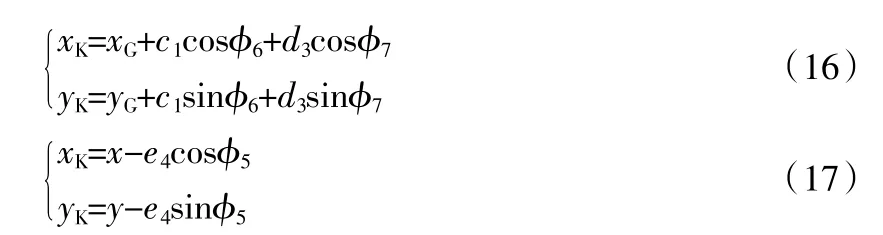
由式（16）和（17）可求得 φ6和 φ7，进而求出 γ1和 β4，从而求出3个个液压缸的驱动尺寸。

3 运动学分析数值算例

设定机构中相邻铰点之间的尺寸关系如表1所示，杆件之间的夹角关系：φ1=70°，φ2=100°，φ3=60°，φ4=50°，φ5=130°。分别设定5组液压缸的不同长度尺寸（表2）时，得出铲斗的位置坐标和姿态角如表3所示（取整数部分）。将表3得到的5组铲斗的位置和姿态角作为反解的已知条件，进行求解得到3个液压缸的5组驱动尺寸，如表4所示（取整数部分）。表3和表4只取整数部分的结果来分析，表2和表4中的液压缸的驱动尺寸完全一致，说明运动学正解和反解分析都是正确的。

表1 相邻铰点之间的尺寸关系 mm

表2 5组不同的液压缸尺寸 mm

表3 铲斗的位置和姿态 mm

表4 反解液压缸的驱动尺寸 mm

4 结论

研究了著名的德国“强力三角”正铲挖掘机的运动学分析，该工作装置完全满足正铲挖掘机的2个水平自由度和1个旋转自由度。采用矢量方程的理念，分析了该工作装置的运动学正反解，并给出实例验证。该分析方法为这种复杂机构的运动学分析提供了一种新的思路。

[1]谢国安.O&K公司液压挖掘机新的联动工作装置[J].矿山机械，1984（6）：53-57.

[2]Hall A S.Characterizing the Operation ofaLargeHydraulic Excavator[D].Australia：The University of Queensland BrisbaneMaster of Philosophy，2003.

[3]Hall A S，Mcaree P R.Robust Bucket Position Tracking for a Large Hydraulic Excavator[J].Mechanism and Machine Theory，2005，40（1）：1-16.

[4]Flores F G，Kecskemethy A，P?ttker A.Workspace Analysis and Maximal Force Calculation of a Face-Shovel Excavator Using Kinematical Transformers[C].12th IFToMM World Congress，Besancon，2007.Besancon，IFToMM：375-381.

[5]丁华锋.运动链的环路理论与同构判别及图谱库的建立[D].秦皇岛：燕山大学，2007.

[6]熊有伦，丁汉，刘恩沧.机器人学[M].北京：机械工业出版社，1993.

[7]高志.机械原理[M].广州：华南理工大学出版社，2011.