玛湖地区低渗透致密砂砾岩储层渗透率模型研究及应用

潘军, 杨国栋

(1.中国石油化工股份有限公司油田事业部, 北京 100728; 2.西安理工大学高科学院, 陕西 西安 710109)

0　引　言

准噶尔盆地玛湖地区百口泉组储层受岩石成分复杂、粒度变化较大、孔隙类型多样等因素的影响,储层孔隙结构非均质性较强,次生孔隙较发育,常规方法计算储层渗透率准确度较低,常规评价方法建立单一回归模型得到的渗透率相关性较差,低渗透储层渗透率的准确表征困难较大[1]。因此,针对复杂砂砾岩储层建立一套可行的渗透率模型,提高该储层渗透率解释精度。Jennings等[2]基于岩石结构系数的渗透率分类计算模型。焦翠华,王志章等[3-4]运用流动单元方法计算储层渗透率,并对其进行分类。邵维志等[5]利用核磁共振测井刻画孔径尺寸空间,将孔隙分为4个区间,并用区间孔隙度计算渗透率。在前人建立渗透率模型研究的基础上,本文利用储层岩心分析数据,结合地质资料,分析影响渗透率的主要控制因素,采用分岩性、多元回归的方法建立适用于低渗透砂砾岩储层的渗透率模型,为砂砾岩储层研究提供新实例,并且为区域油气勘探提供参考。

1　储层基本特征

1.1　岩性特征

收集整理了研究区6口井104张岩心扫描电镜照片。按照岩石颗粒大小分类,可将研究区储层段的岩性分为4类:细砾岩,占储层段岩性的62.14%;小中砾岩,占储层段岩性的28.25%;大中砾岩,占储层段岩性的6.73%;砂岩(以细砂岩和细-粉砂岩为主),占储层段岩性的2.88%(见图1、图2)。

图1　研究区百口泉组储层段岩心电镜扫描照片

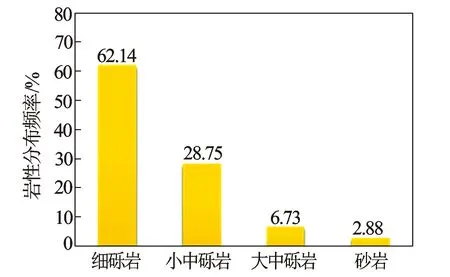
图2　研究区百口泉组岩性统计频率直方图

1.2　物性特征

从研究区6口井217块岩心物性分析看,样品孔隙度分布范围4%～13%,5%～11%区间的孔隙度占全部样品的84.77%,其中样品峰值对应孔隙度为5%～7%,占样品总数的43.7%,孔隙度大于11%的相对高孔隙度段样品占样品总数的5.96%。渗透率主要分布范围(0.1～10)×10-3μm2,占样品总数的95.36%,其样品峰值对应渗透率为(1～5)×10-3μm2,渗透率小于0.1×10-3μm2占4.6%,渗透率大于5×10-3μm2占20.5%。分析认为研究区百口泉组储层为低孔隙度低渗透率储层。由于储层岩性颗粒粒级分布范围广,非均质性强,岩石孔隙结构复杂,孔隙度渗透率关系较差(见图3)。

图3　研究区百口泉组孔隙度渗透率关系图

2　储层渗透率模型建立的方法

2.1　渗透率影响因素分析

图4　研究区不同岩性、孔隙类型与物性的关系

(1) 岩性对渗透率的影响。储层物性直接受岩石岩性影响。根据收集到取心分析资料和物性分析资料,建立了研究区储层岩性与物性的关系图[见图4(a)]。结果表明,岩心分析孔隙度细砾岩和小中砾岩平均值最大,砂岩次之,大中砾岩物性最差,主要是由于岩性复杂和岩石成分多样作用影响。因此,研究区百口泉组储层优势岩性为细砾岩,其次是小中砾岩,岩性对储层渗透率影响较大。

(2) 孔隙类型对渗透率的影响。对研究区岩心铸体薄片统计分析,并结合物性资料进行了统计分析,结果表明,研究区百口泉组储层孔隙类型微裂缝及収缩孔发育,成岩过程中对孔隙微孔化及孔隙之间的连通起到了重要作用,渗透率好;粒间溶孔和粒内溶孔发育较多,但成岩过程中的压实作用导致孔隙之间的连通性较差,渗透率一般;剩余粒间孔的渗透率最低,因为该地区储层黏土含量较高,堵塞了粒间孔的毛细管通道[见图4(b)]。

(3) 黏土含量对渗透率的影响。收集整理研究区39块岩心样品的全岩分析黏土含量与岩心分析渗透的关系发现,渗透率随着黏土含量增大而明显降低(见图5),由于该地区岩石成分主要以火山凝灰岩为主,且溶蚀作用,使黏土堵塞了孔隙喉道,阻碍了孔隙的连通性[6]。

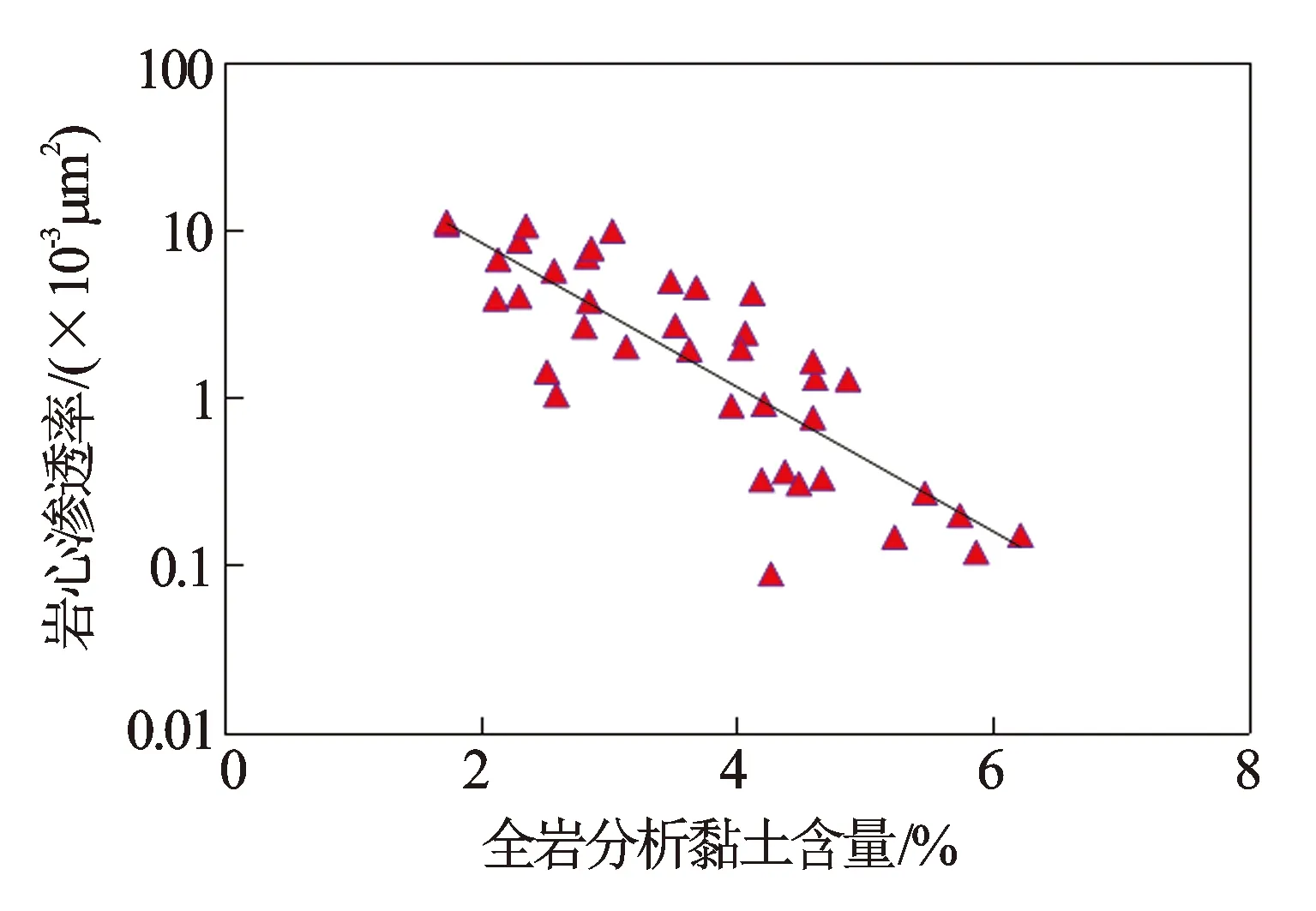
图5　研究区全岩分析黏土含量与岩心分析渗透率的关系

2.2　分岩性多元回归法求解储层渗透率

(1) 常规方法建立渗透率模型。根据取心资料,对研究区的物性资料进行深度归位,并与地质资料进行了对比分析,利用正确归位后的物性资料建立常规渗透率模型

K=0.056φ1.607

(1)

式中,K为渗透率,×10-3μm2;φ为孔隙度,%。

(2) 分岩性多元回归方法建立渗透率模型。通过对影响因素的分析发现不同岩性的渗透率差异较大,细砾岩渗透率最好,其次是小中砾岩,最后渗透性差的砂岩和大中砾岩,黏土含量和渗透率呈负相关,规律较明显。因此,根据实际资料分岩性建立岩心渗透率与孔隙度、黏土含量的关系,即K=f(φ,Vsh),岩心渗透率与岩心孔隙度、测井计算黏土含量进行多元回归拟合,建立储层渗透率测井计算模型(见图6)。

细砾岩:K=e(2.469log (φ/100)-2.733log (Vsh/100)-1.044

(2)

小中砾岩:K=e(4.287log (φ/100)-0.385log (Vsh/100)+4.87

(3)

大中砾岩:K=e(4.775log (φ/100)-1.93log (Vsh/100)+2.479

(4)

砂岩:K=e(3.813log (φ/100)-3.985log (Vsh/100)-0.73

(5)

式中,K为渗透率,×10-3μm2;φ为孔隙度,%;Vsh为黏土含量,%。

3　应用实例

以AH-9井为例,利用常规的渗透率模型计算的测井渗透率和分岩性多元回归方法计算渗透率,对比两者计算的结果,利用分岩性多元回归的渗透率计算模型准确性更高(见图7)。

图7　研究区AH-9井渗透率计算成果图*非法定计量单位,1 ft=12 in=0.304 8 m,下同

4　结　论

(1) 岩性不同的岩石渗透率差异较大、次生孔隙的渗透率比原生孔隙的较好、渗透率随着黏土含量的增大而降低。

(2) 提出了在分岩性的基础上,对孔隙度和渗透率进行多元回归建立渗透率模型,并与常规单孔隙度计算渗透率模型进行了对比,改进的渗透率模型计算结果更准确。