基于信息熵分析的量子随机数扩展

（北京信息科技大学，北京 100192）

温婉琳，郑小博，李 宁，郑小博（通讯作者）

1 BB84量子密钥分发协议

在密码学中，“一次一密”作为绝对安全的加密方式，已经得到证明，基于量子力学原理，QKD协议应运而生。1984年，为增加安全通信距离、提高安全成码率和现实系统安全性，国际上首次提出BB84协议，实现了为分隔两地的用户提供无条件安全的共享密钥。

BB84协议的运行流程分为四步：制备、测量、对基以及后处理。

基于安全性基础与前提假设，BB84协议过程具有无条件的安全性。

2 量子随机数

随机数在很多领域是一个重要的概念，一方面，随机数在密码学、算法、仿真、博彩业和量子密钥分配等领域是一种重要资源，另一方面，判断一个过程是否产生好的随机数本身也是一个基础的科学问题。

在QKD协议运行过程中，随机数的产生对于制备阶段有着举足轻重的作用。尽管量子随机数发生器利用量子过程中的固有随机性产生真随机数并且目前已经有很多设备可以达到代替经典随机数发生器的水平，但随着我们日益增长的需求，随机数的数量的缺乏问题显得尤为突出。

例如，京沪干线传输的数据过于庞大，量子随机数供不应求。

综上，如何产生高质量的大量随机数是我们当下所要探索的新课题。

3 解决方案

量子传输过程中的“一次一密”保证了数据传输的绝对安全性，但是在实际生活中，并不是所有的数据传输都需要如此“高等级”的加密，所以针对不同的需求，我们应当适当的降低其安全程度，以满足其传输速率优先的主要需求。

3.1 随机数生成

我们定义新的规则：

对一串量子比特进行划分，前m位我们定义为f（x），表示我们可以按需最多由这串bit产生（2的m次方-1）个字符串。m后的n位我们定义为g（x），可随机取值0或1，0代表对产生的新bit串做单位变换，1表示对产生的新bit串做SHA2变换。这样我们就可以利用原量子bit来产生足够多的新字符串来丰富我们的随机数池。

大量的随机数产生完毕之后，我们可以将其切分，嵌入到量子bit中，从而产生大量高质量的随机数。

3.2 解决步骤

本课题解决思路如下：1）随机生成20的数字；2）定义fx的位数m；

3）利用QKD密钥分配方法产生2^m-1个随机数；

4）根据g（x）的值，对随机数做单位变换或者SHA变换；5）将生成的16进制数转换为十进制数存储；

6）计算前一位随机数和后一位的随机数的信息熵分析其安全性。

依据QKD量子密钥分发的步骤，实验包括加密、解密，以及对随机数的验证。

3.3 数据的传输

量子密钥分配技术（QKD技术）就可以保证传输信息传输的安全性。本文采用QKD技术来产生量子随机数，在以上大量高质量随机数的支持下，结合QKD安全的协商过程，便可保证协商的高效性与安全性。

3.4 数据的同步

保证同步通信采取的策略是每个信息帧的开始用同步字符来指示，其次还要保证发送和接收双方采用同一时钟，在传送数据的同时要传送时钟信息，以便接收方可以根据时钟信号来定位每个信息位，从而达到接收与发送的同步。

4 实用性分析

4.1 抵御明文攻击

g（x）的随机性在一定程度保证了大量相同数据传输的安全性，有效的防止窃听方进行暴力破解。

4.2 灵活与高效

f（x）、g（x）函数均具有随机性，随机数的数量可以由我们的需要而变化，具有一定的灵活性和高效性。

5 基于信息熵的安全性分析

随着互联网技术和计算机设备的高速发展，人们对信息的处理能力也在不断地提高，这标志着人们已经进入了信息时代，而信息论是信息时代不可不提的重要理论，它包括了通信，密码学、数据的传输，信息熵、数字压缩等等许多的学科，信息论使我们可以对不确定的数据进行确定的描述。其中信息熵因其在评估不确定信息上的天然优势，作为此次安全性分析的选择。

5.1 信息熵定义

信息熵是一个数学上颇为抽象的概念，我们可以把信息熵理解成某种特定信息的出现概率（离散随机事件的出现概率）。

一个系统越是有序，信息熵就越低；反之，一个系统越是混乱，信息熵就越高。信息熵也可以说是系统有序化程度的一个度量。随机数安全性利用计算出的信息熵进行分析。

对我们而言，信息熵即可反映这串随机数的安全程度，信息熵越，则表明这串随机数越安全，信息熵越低，则安全性越低。

5.2 解决方案

我们计算f（x）位数变化前后信息熵的比值，来评估随机数的不确定性以及安全性。

6 实验数据

6.1 随机产生的一组随机数

初始我们定义f（x）的位数为12，即m=12，将会产生对应随机数。

6.2 安全性变化曲线图

通过f（x）位数的不断变化，信息熵的比值呈图1，横坐标为“f（x）的位数”，纵坐标为“生成随机数的平均信息熵与原始数据比值的变化量”

如图1表示生成的量子随机数比原始数据的信息熵高，生成的量子随机数的不确定性高，因此，新生成的量子随机数的安全性可以保证。

7 实验结果分析

综上，通过对新规则的实际验证，可以证明，通过上述方案，在扩大随机数数量同时，安全性也可以得到保证，此方案再进行完善之后可以作为一种扩大随机数的方案进行利用。

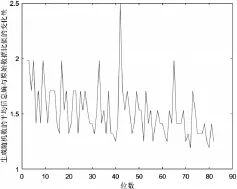
图1 安全性变化曲线

[1] 杨佳玉.量子通信协议设计与安全性检测研究[D].北京邮电大学，2015.

[2] 王蕾.量子时钟同步与量子相干控制[D].陕西师范大学，2010.