基于蒙特卡洛模拟法的输电塔架结构可靠度分析

牛群凯, 朱 瑞, 朱全军, 任建兴, 王苏民, 吴世伟, 陈达多

(1.上海电力学院, 上海 200090; 2.全球能源互联网研究院, 北京 102211)

随着我国十三五纲要的稳步推进和特高压技术的快速发展,输电线路塔架作为高负荷电能的输送载体,成为特高压输电线路工程建设中的核心。如何在保证经济合理的前提下,建设安全可靠的输电线路塔架一直是研究的热点和难点[1]。为了考虑和解决工程结构设计中所遇到的诸多不确定性问题,结构的可靠度理论随之产生和发展,因此随机不确定性下的铁塔可靠度问题可以应用结构可靠度理论进行研究[2]。熊卫红等人[3]将基础沉降和风荷载作为输入变量,利用矩方法计算塔线体系的可靠度,研究结果表明,基础沉降较风荷载对杆塔结构可靠度影响更大;张卓群等人[4]对角钢塔和钢管塔进行可靠度对比分析,发现钢管塔构件可靠指标大于角钢塔,且实际构件可能达不到工程实际要求可靠度。目前研究中多以无关变量为输入变量,但二次函数往往存在变量交叉项,对于可靠度计算具有不容忽视的影响,因此本文基于蒙特卡洛模拟法对风荷载和覆冰荷载作用下的输电塔架进行可靠度分析,并考虑变量的相关性问题,以期为输电塔架的可靠度计算和设计提供理论指导。

1 可靠度基本理论

设X=(X1,X2,X3,…,Xn)T是影响结构功能的n个基本随机变量,则随机函数如下

Z=g(X)=g(X1,X2,X3,…,Xn)

(1)

Z为结构的功能函数,也称为结构的失效函数。若Z>0则结构可靠;Z<0则结构失效;Z=0表示结构处于极限状态。结构的极限状态方程为

Z=g(X)=g(X1,X2,X3,…,Xn)=0

(2)

当功能函数只有两个随机变量R和S时,相应的极限状态方程可简化为

Z=g(R,S)=R-S=0

(3)

可靠概率pr表示结构完成预定功能的概率;相反,失效概率pf表示结构不能完成预定功能的概率。

用标准差σZ度量原点到平均值μZ的距离,所以有

(4)

β是一个无量纲参数,称为结构的可靠性指标或可靠指标,可表示为

pf=Φ(-β)=1-Φ(β)

(5)

β与可靠概率pr之间的关系为

pr=Φ(β)

(6)

2 失效模式的功能函数

塔架在设计和实际运行中往往要考虑到风荷载和覆冰荷载作用下的变形和位移问题,研究手段也多以有限元软件模拟分析为主,进行功能函数的拟合和分析。

采用某110 kV线路SJ1干字型转角塔的工程实际数据来建立输电塔的有限元模型。塔架主材采用Q345B角钢,所有斜材和辅助材料均采用Q235B角钢,相应的有限元建模参数如表1所示。采用梁单元BEAM188为建模单元,建立有限元模型如图1所示。

表1 有限元模型基本参数

图1 有限元模型三维示意

自重荷载和覆冰荷载通过改变材料密度的方法加载在塔架结构模型上。采用拟静力的方法,将风荷载等效为作用于塔架模型截面的集中荷载,将计算所得到的集中荷载平均施加到截面的各个节点上,重合节点上的集中荷载进行叠加,方向沿横线路向,与塔架呈90°夹角[5]。

以主材在覆冰厚度H为10 mm时的情况来计算其在覆冰后的相应属性。主材覆冰前的尺寸为63 mm×5 mm,覆冰后为73 mm×25 mm,覆冰后的挡风面积为

S=73×25×2-25×25=3 025 (mm2)

(7)

覆冰前主材的密度为7 850 kg/m3,取长度为1 m的主材,则覆冰后的质量为

(8)

则覆冰10 mm后的主材密度为

(9)

根据式(7)、式(8)和式(9)依次计算出覆冰厚度H为20 mm和40 mm时,主材密度ρ分别为1 774.83 kg/m3和1 328.19 kg/m3。

由GB 50135—2006《高耸结构设计规范》规定可知[6],作用在输电塔架上的风荷载标准值ωs的计算公式为

式中:βz——塔架风荷载调整系数;

μs——风荷载体型系数;

μz——对地高度为z处的风压高度变化系数;

ω0——基准风压标准值;

As——承受风压投影面积;

v′——基准高度处的风速。

将作用在塔架上的风速v和覆冰厚度H为输入变量,输电塔架的最大位移Dmax为输出变量,利用有限元软件ANSYS模拟得到的数据样本如表2所示。

通过MATLAB软件中的曲线拟合工具箱,对表2中数据进行功能曲线拟合。由于功能函数是多项式隐函数,因此选用多项式稳健拟合,拟合结果如下。

一次回归函数为

(12)

二次回归函数为

(13)

一次回归函数和二次回归函数拟合图分别如图2和图3所示。由图2和图3可知,拟合结果符合要求,拟合效果较好。

表2 不同风速和覆冰厚度下塔架最大位移样本

图2 一次回归函数拟合示意

图3 二次回归函数拟合示意

以刚度失效为塔架的失效模式。当塔架的最大位移超过一定极限时,则塔架结构失效。设极限位移为塔架高度Ht的1/1 000,建立一次功能函数如下

Z=10-3Ht-Dmax

(14)

整理可得

(15)

由式(15)可知,功能函数Z是v和H的一次函数,且随着v和H的增大而随之减小,这是由于塔架的最大位移Dmax随着风速v和覆冰厚度H的增大而增大。当Z≤0时,塔架结构失效。

为了讨论可靠度分析中风速和覆冰厚度的敏感性,选择仅含一次项的功能函数为研究对象,则有

由式(16)和式(17)两个偏导数可知,功能函数Z与风速v和覆冰厚度H均为负相关。另外,关于H的偏导数的绝对值小于关于v的偏导数数值,因此功能函数Z关于风速v的变化率更加明显,即相对于覆冰厚度H,风速v是塔架可靠度分析中更为敏感的因素。

当其中随机变量H为定值时,此时一次功能函数是另一个随机变量v的单调函数,二次功能函数则是v的二次函数,单调性由v的取值区间决定,即二次功能函数为

(18)

当风速v=30 m/s时,二次功能函数为

(19)

函数图像如图4所示。由图4可知,随着覆冰厚度H的不断增加,功能函数的函数值逐渐递减,塔架结构可靠度逐渐减小,结构趋向失效。

当覆冰厚度H=20 mm时,二次功能函数为

(20)

函数图像如图5所示。由式(20)和图5可知,功能函数Z的函数值随着风速v的增加先递增后递减,结构可靠度呈现相同的变化趋势;当v=0.4 m/s时,Z达到最大值,即0.045 81。

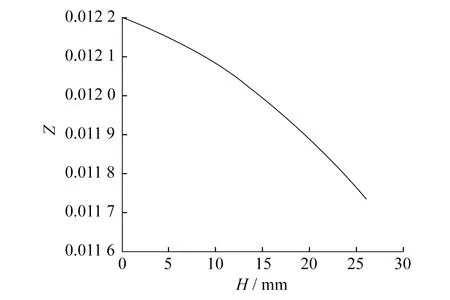
图4 风速v=30 m/s时二次功能函数曲线

图5 覆冰厚度H=20 mm时二次功能函数曲线

3 可靠度计算

蒙特卡洛模拟法被广泛用于计算已知概率分布的随机变量。该方法具有不断重复的模拟过程,通过每一次模拟,由概率分布生成的随机变量值,从而得到解的数据样本。若总共进行了N次模拟,则Z<0出现了nf次,根据Bernoulli定理,结构的失效概率为:

(21)

式中:Ωf——失效域;

fX(x)——联合概率密度函数;

x——样本值;

I(·)——指示函数;

gX(x)——结构的功能函数。

由式(5)和式(21)即可求得结构可靠指标β。采用MATLAB软件编程计算结构可靠指标β,可以直接产生服从各相应概率分布函数的随机变量数组,从而大大简化了编程过程[6],极大地方便了计算。程序流程如图6所示。

图6 蒙特卡洛模拟法程序流程

利用MATLAB软件,对输电塔在风荷载和覆冰荷载作用下的可靠性进行分析,将塔架上的风速v以及覆冰厚度H定义为随机输入变量,将输电塔最大位移定义为随机输出变量。风速v和覆冰厚度H两者均服从极值Ⅰ型分布;期望分别为30 m/s和20 mm;变异系数分别为0.1和0.181[7]。

考虑风速v和覆冰厚度H两个变量完全相互独立时,设极限位移为塔高的1/1 000,由已建立的一次功能函数,计算可得塔架的可靠指标β为1.523 1。

为了更好地进行比对分析,分别计算当某一变量为定值且另一变量变化时,塔架结构的可靠度变化情况。为简化计算,仅分别考虑风速v为30 m/s时和覆冰厚度H为20 mm时的塔架可靠度,具体计算结果见表3和表4。

由表3和表4可知,随着风速和覆冰厚度的增大,结构的可靠概率和可靠指标也随之降低;当风速一定时,覆冰厚度的增大对可靠概率和可靠指标的影响有限;但当覆冰厚度一定时,随着风速的增加,塔架的可靠概率和可靠指标急剧下降。由此可见,相对于覆冰厚度,风速在塔架可靠度分析中为更敏感的因素。这与前文中功能函数表达式分析结果相吻合。但以上分析都基于覆冰厚度和风速是相互独立的随机变量,而实际工程环境中两变量是存在相关性的,因此本文对具体的相关性进行分析。

表3 风速v=30 m/s时不同覆冰厚度下塔架的可靠度

表4 覆冰厚度H=20 mm时不同风速下塔架的可靠度

4 变量相关性分析

当由一次功能函数计算Z的期望时,随机变量间没有交叉项。但根据二次功能函数求Z的期望时,由于两随机变量之间存在交叉项,且对计算结果有很大影响,因此往往需要考虑随机变量之间的相关性问题。随机变量v和H的线性相关系数为

(22)

式中:μ(·)——随机变量的期望;

σ(·)——随机变量的方差。

由式(22)可知

(23)

(24)

结构的可靠指标β为

(25)

以工况H=20 mm且v=30 m/s为例进行计算,研究在不同相关系数下输电塔架的可靠度,结果如表5和图7所示。

表5 不同相关系数下塔架的可靠度验算

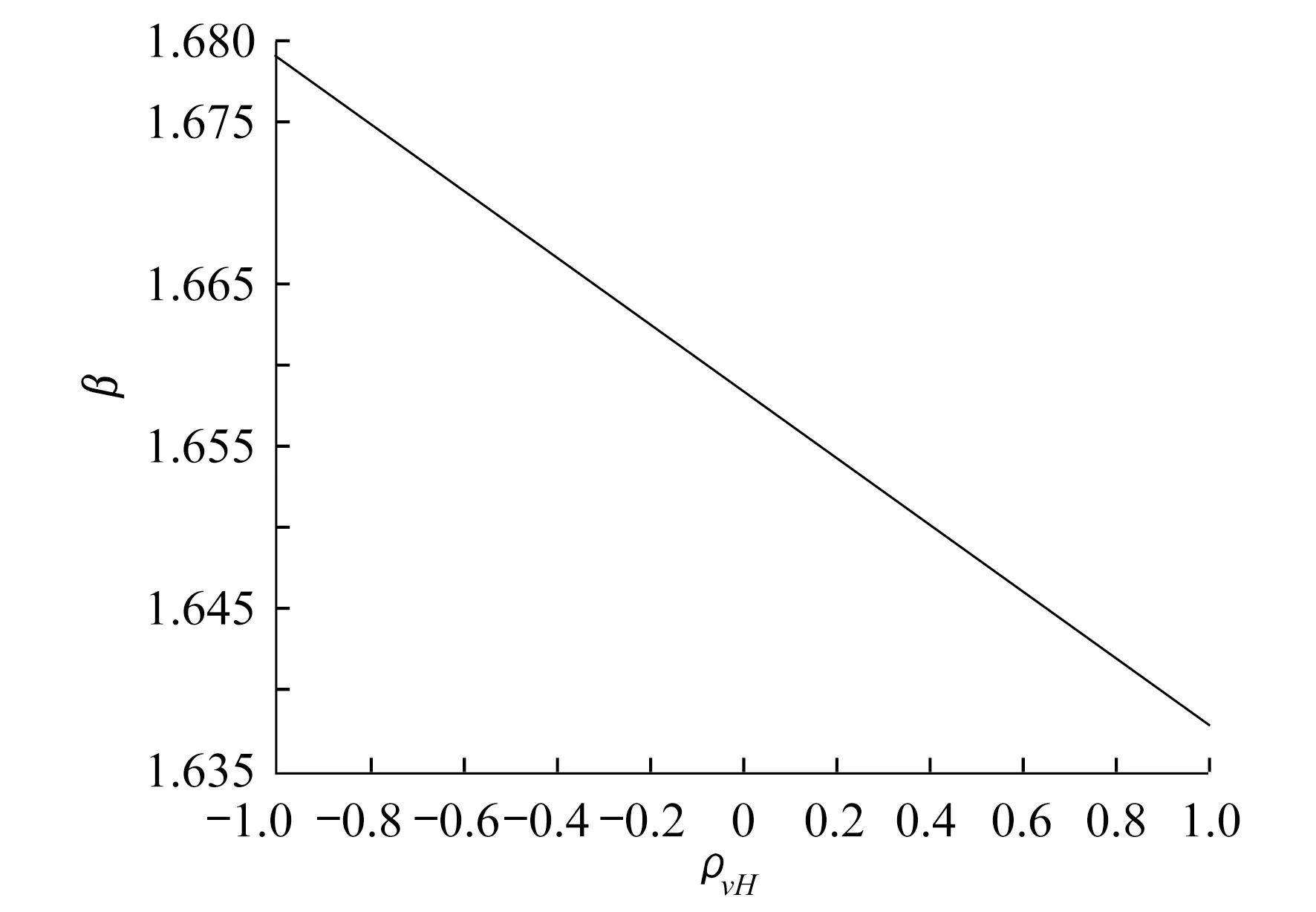
图7 可靠指标与相关系数关系

由表5和图7可知,当相关系数增大时,可靠指标随之减小,且两者变化呈现线性相关;当相关系数取值为-1时,此时随机变量之间为完全负相关,可靠指标达到峰值;当相关系数分别取-1和1时,两者对应的可靠指标相差了2.5%。由此可见,随机变量的相关性在可靠度计算中不容忽视。

5 结 论

本文将可靠度分析理论和蒙特卡洛模拟法应用于输电线路塔架的可靠度计算中,主要研究结论如下。

(1) 采用MATLAB软件中多项式稳健拟合得到风荷载和覆冰荷载下的一次回归函数和二次回归函数,通过对函数表达式和函数图像分析可知,随着风速和覆冰厚度的增大,塔架的最大位移增大,当Z≤0时,塔架结构失效,且风速比覆冰厚度在塔架可靠度分析中具有更高的敏感性。

(2) 在可靠度计算中使用蒙特卡洛模拟法,基于建立的一次功能函数,利用MATLAB软件计算得到塔架的可靠指标β为1.523 1。同时也对仅有单一变量情况时的可靠概率和可靠指标进行验算。计算结果表明,当风速一定时,随着覆冰厚度的增大,可靠概率和可靠指标降低幅度有限;当覆冰厚度一定时,随着风速的增加,塔架的可靠概率和可靠指标急剧下降。

(3) 在推导计算出二次功能函数中交叉项的相关系数及塔架可靠指标表达式后发现,当覆冰厚度和风速一定时,随着相关系数的增大,可靠指标随之减小,且两者变化呈现线性相关;当相关系数取值为-1时,可靠指标为最大值,当相关系数取1时,可靠指标为最小值,两者的可靠指标相差了2.5%,因此在可靠度计算中应注意随机变量的相关性影响。

参考文献：

[1] 刘玉龙,李文强.基于四阶矩的输电塔抗风可靠度分析[J].空间结构,2017,23(1):75-79.

[2] 李会军,徐士博,唐业,等.输电塔结构的可靠度及敏感性评估[J].钢结构,2016,31(9):39-45.

[3] 熊卫红,刘先珊,李正良,等.500 kV输电线路基础沉降铁塔的可靠度分析[J].电力建设,2015,36(2):41-47.

[4] 张卓群,李宏男,贡金鑫,等.输电塔结构可靠度分析[J].电力建设,2014,35(5):34-41.

[5] 孔伟,刘玉龙.输电塔在大风覆冰下的可靠度分析[J].武汉理工大学学报,2015,37(4):59-64.

[6] 中华人民共和国建设部,中华人民共和国国家质量监督检验检疫总局.高耸结构设计规范:GB 50135—2006[S].北京:中国计划出版社,2006.

[7] 陈卫东,李建操,于艳春,等.多工况下输电铁塔结构系统可靠度计算[J].工程力学,2013,30(S1):180-183.