水平井套管下入摩阻力学分析
李庆明
套管下入过程中大钩载荷的预测是水平井成功完井的关键因素之一,水平井由于其特殊的井眼轨迹,在下套管的过程中摩阻要比常规井大。尤其在大斜度井段和水平井段,套管对井壁的侧压力很大,从而大大增加了下套管摩擦阻力。因此,准确地预测套管下入摩阻对水平井钻井的设计和施工具有重要的指导作用。
1 模型建立
假设套管与井壁连续接触,套管柱轴线与井眼轴线一致,计算单元段所受重力、正压力、摩阻力均匀分布,且为空间斜平面上的一段圆弧。
1.1 单元力学模型分析
水平井中的管柱随着井身轨迹的变化而弯曲,实钻井身轴线是一条不规则的三维空间曲线[1-4]。在进行具体分析时,将井身轴线视为空间斜平面内的一段圆弧,建立空间笛卡尔坐标系ONEH如图1所示,其中N() 轴、E() 轴、H()轴分别指向正北、正东和重力方向,井段AB位于空间某一斜平面R上。
取上端点A为坐标原点,上端点A、下端点B的井斜角和方位角分别为αA、ΦA和αB、ΦB,(°)。在A点和B点分别作切线AC和BC相交于C点。由切线AC和BC所确定的空间斜平面R即井身平面,它的位置可由其法线向量表征。由向量和所确定的铅垂平面P即为井斜平面。Q平面为通过直线AB且与P平面正交的平面,即方位平面。

图1 三维分析的坐标系图
根据井眼轨迹数据将管柱分为若干个计算单元。作用在长度为ΔL(设为AB段)的管柱单元上的力有:Ti,Ti-1为管柱单元上下端的轴向力,N;N为管柱单元与井壁的接触正压力,N;Wg为单位长度管柱的浮重,N;Fμ为管柱单元的摩阻力,N;以管柱单元中点为原点,以中点的切线为x轴,xy平面与R平面重合,根据右手定则确定z轴,建立局部坐标系xyz。在局部坐标系中管柱单元受力情况如图2所示。
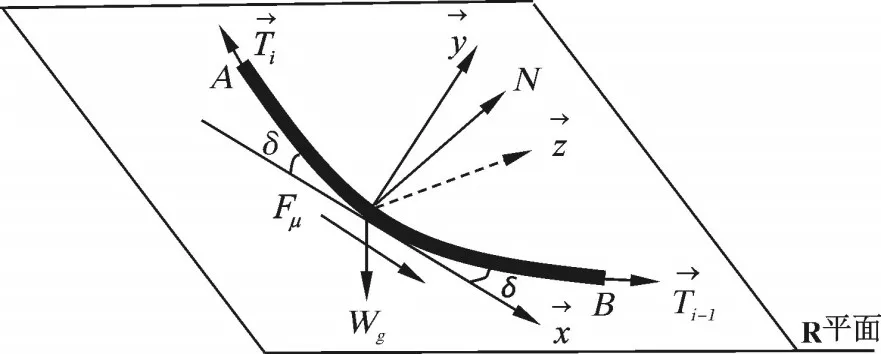
图2 单元在局部坐标系下的受力
在大地坐标系中,斜平面R的法向向量:

切线AC和BC的夹角即为狗腿角,根据余弦定理,则有

斜平面R的倾角θ为×与重力向量( 其单位向量为)的夹角,也即向量与z轴的夹角:

根据管柱单元在三个坐标方向上的力学平衡建立如下方程,则有:

其中,各量计算公式及说明如下:

②单元管柱在钻井液中的重力分布为:

③摩阻力:

④重力分量Ng在R平面上投影与x轴的夹角:

管柱单元平均井斜角:

式中:we为管柱单元在空气中的单位重量,N/m;ρd为钻井液的密度,kg/m3;ρs为钢材密度,kg/m3;μ为摩擦系数;“-”表示管柱向下运动。
1.2 单元摩阻求解
将管柱划分为多个微单元,根据以上方程,给定初始条件(钻压和钻头扭矩)的情况下,从钻头向上迭代求解,逐段进行求解即可得全井段的摩阻和轴向力[5-14]。
根据建立的水平井摩阻三维计算模型,采用三次样条插值方法处理井眼轨迹数据插值。在分析过程中,首先进行管柱单元划分,然后按照划分单元计算单元测点的摩阻力学分析所需要的参数,最后从井底(钻头处)开始,对管柱单元逐步求解递推到井口即可实现全井的力学分析。计算流程如图3所示。

图3 计算流程图
2 现场应用实例
应用该模型对辽河油田某一区块的水平井进行计算。该井的井身结构如图4所示。该井的设计井深1 687 m,最大井斜角98°,水平位移876 m,计算用钻井参数钻压50~120 kN,转速70 r/min,钻井液密度1.15 g/cm3,套管内摩阻系数取为0.25,裸眼内系数取为0.3。
应用本模型对该井下技术套管过程进行受力分析,计算结果如图5所示。通过计算摩阻力为151.1 kN,井口轴向载荷为482.2 kN,实测大钩载荷为518 kN,误差为6.9%,满足工程要求。

图4 井身结构图

图5 下套管过程轴向载荷预测结果图
3 结论
1)根据空间斜平面假设建立了适合水平井的下套管摩阻三维计算模型。计算模型简单、计算方法可靠,通过现场验证,计算结果精度较高。
2)井下管柱的摩阻扭矩问题始终是钻井界关注的重点和难点,进一步研究和完善适合各种井型的摩阻扭矩预测模型仍是今后努力的方向。
[1]白家祉,苏义脑.井斜控制理论与实践[M].北京:石油工业出版社,1990.
[2]张林强.大位移井摩阻扭矩计算模型[J].断块油气田,2008,15(2):88-91.
[3]Johansick CA.Torque and Drag in Direction Wells Prediction and Measuremen[J].Journal of Petroleum Technology,1984,36(6):987-992.
[4]Sheppard M.C,Wick C,Burgess T,et al.Designing Well Paths To Reduce Drag and Torque[J].SPE Drilling Engineering,1987,2(4):344-350.
[5]秦永和,付胜利,高德利.大位移井摩阻扭矩力学分析新模型[J].天然气工程,2006,26(11):77-79.
[6]李子丰,刘希圣.水平井钻柱稳态拉力—扭矩模型及其应用[J].石油钻探技术,1992,20(4):1-6.
[7]张建群.定向井中摩擦阻力模式及其应用的初步研究[J].大庆石油学院学报,1989,13(4):6-11.
[8]韩志勇.井眼内钻柱摩阻的三维和两维模型的研究[J].石油大学学报(自然科学版),1993,17(增):44-49.
[9]闫 铁,张建群,孙学增,等.大庆水平井摩阻力分析[J].大庆石油学院学报,1995,19(2):1-5.
[10]闫 铁,马红滨,谷玉堂,等.钻柱在水平分支井段中的摩阻力分析[J].科学技术与工程,2010,10(22):5 378-5 380.
[11]代 奎,闫 铁.水平井井眼摩阻因数的确定方法[J].大庆石油学院学报,1995,19(3):5-8.
[12]马善洲,韩志勇.水平井钻柱摩阻力和摩阻力矩的计算[J].石油大学学报(自然科学版),1996,20(6):24-28.
[13]白家祉.纵横法对钻具组合的三维分析[J].石油学报,1989,10(2):60-66.
[14]An H,Scott SL,Langlinais JP.Estimation bottom hole pres⁃sure in pumping oil wells:effect of high viscosity fluids and casinghead pressure[R].Dallas:SPEAnnual Technical Con⁃ference and Exhibition,2000.

