不可压缩流条件下冲压过滤装置的取样流量

刘龙波， 吴艳敏， 武 山， 周国庆， 李志明

(西北核技术研究所, 西安 710024)

在大气颗粒物污染和辐射环境的监测中，对大气气溶胶取样后再分析是一种常用的方法。[1]，也有将取样设备装载在车辆[2]或飞机[3]等运输平台上进行移动式取样监测,以提高监测的时效性和空间分辨率，这对紧急事件的监测具有重要价值。在取样动力方面，一般是由平台提供电力或配置发电设备，驱动抽气泵作为取样动力[2-3]；还可以利用平台在行进中产生的冲压作为取样动力进行气溶胶取样。这种冲压过滤式方法避免了在平台上装载取样动力设备，减小了平台的质量负载和电力负载，简化了取样装置，尤其是放射性气溶胶监测要求取样体积较大[1]，这种方法的优势更加明显。在以抽气泵为动力的气溶胶取样装置中，取样流量是完全可控的，但在冲压过滤式取样装置中，取样流量是由平台的行进速度和过滤装置的参数共同决定，因此需要分析计算。

在大气层核试验的穿云取样中，曾使用超声速飞机或火箭为平台的冲压过滤式气溶胶取样装置[4-5]，其平台速度约为2Ma。随着大气监测的广泛开展, 近些年来，在较低速度的平台(比如气象航测飞机或无人机)上开展气溶胶取样监测越来越广泛[6]，因此有必要讨论在较低速度下冲压过滤装置的流量计算。原理上，当空气流速小于0.3Ma时，可以认为空气是不可压缩的[7]。在这种条件下，冲压过滤装置中的取样流量的计算方法与超声速平台[4-5]是不同的，但目前尚未见文献报道。本文将推导较低速度下冲压过滤装置的取样流量与速度的关系，并进行实验验证，然后讨论行进速度和高度等因素对取样流量的影响。

1 冲压过滤装置中取样量的计算

1.1 机械能守恒原理

冲压过滤取样原理示意图如图1所示。当取样器随运输工具在大气中行进时，由于来流的冲压，会有一部分空气进入取样器。进入取样器的气体中的气溶胶颗粒物被过滤装置捕集，尾气排出取样器。

图1 冲压过滤取样原理示意图Fig.1 Schematic of aerosol filter sampling by kinetic pressure

根据流体机械能守恒原理，忽略取样器壁面的摩擦阻力，则取样器行进的冲压与取样器内气流的动压之差应与过滤装置的压阻相等，即：

(1)

虽然在不可压缩流条件下一般设定空气密度不变，但在过滤装置中通常会产生显著的压差，影响密度。本文假设过滤装置前后空间内的静压和空气密度分别一致，过滤装置前后的静压差值为过滤装置的压阻。取样器内的空气平均密度和压力则分别为过滤装置前后空气密度和压力的算数平均值，而根据气体连续性方程，取样器内空气的平均速度用调和平均值[8]：

(2)

式中，u1和u2分别为取样器内过滤装置前后的空气流速，m·s-1。

1.2 过滤装置的压阻

一般地，当气体流速较低时，过滤装置的压阻与气体流速成正比[9]，当气体流速较高时，过滤装置的压阻则是流速的二次方函数[10]。一般研究中采用过滤装置前的表面流速[9-10]，当过滤装置压阻较大时，宜采用气体平均流速[8]。因此，考虑过滤装置的压阻为

(3)

式中，η为空气黏度，Pa·s；a1和a2为拟合参数。

采用纤维滤材或颗粒床等经典结构的过滤装置，对经验参数a1和a2均可以进行计算，但本文研究的过滤装置的结构比较复杂，在实验中，很难控制黏度和密度都不变，a1和a2需通过实验测试拟合得到，采用式(4)[8]来进行压阻和流速实验数据拟合。

(4)

式中，ρ*和η*分别为无量纲的相对密度和相对黏度，有：

(5)

式中，ρs=1.293 kg·m-3，为标准状态下空气密度。

(6)

式中，ηs=1.708×10-5Pa· s，为标准状态下空气黏度。

空气黏度一般只与温度有关[11]：

(7)

式中，Ts=273.15 K，为标准状态下温度。

1.3 冲压取样流量推导

假设空气性质满足理想气体状态方程，取样过程中温度不变，且取样器中过滤装置前静压与取样器前静压相等(p1=p0)。

在计算压阻时，可以将式(4)简化成：

(8)

将式(8)代入式(1)，有：

(9)

将式(5)代入式(9)得：

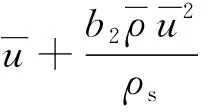
(10)

另根据理想气体状态方程和p1=p0，有：

(11)

将式(1)代入式(11)，有：

(12)

整理得：

(13)

将式(13)代入式(10)，得：

(14)

整理可得：

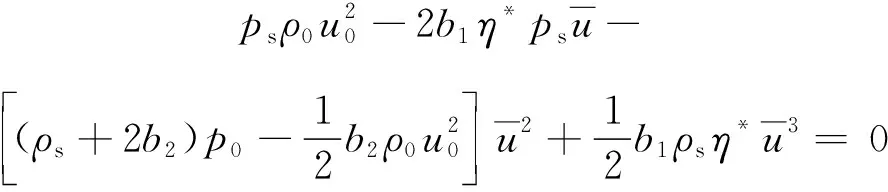
(15)

式中，ps为标准大气压，101 325 Pa。

(16)

(17)

式中，A为过滤装置横截面积，m2；Qv为工况体积取样流量，m3· s-1。

2 计算方法的实验验证

本文设计加工了一个取样器，并在陕西省计量院标准流量装置上对过滤装置的压阻性能进行了测试。利用式(4)对实验测试数据进行了拟合，拟合结果如图2所示。从图2可以看出，实验测得的气体流速和压阻的关系与式(4)符合，得到拟合参数b1= 101.9 Pa· s·m-1，b2= 5.392 Pa· s2·m-2。

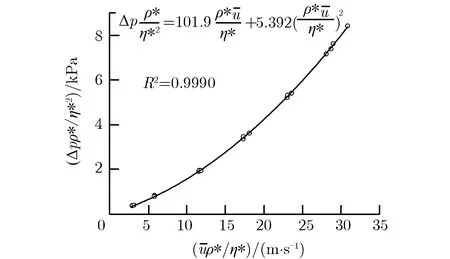
图2 过滤装置压阻和气体流速的关系Fig.2 Pressure drop vs. the flow velocity of the filter

在中国空气动力研究与发展中心的低速风洞(风速0～110 m· s-1)和高速风洞(100～170 m· s-1)中分别对取样器进行了固定风速下的取样流量测试。使用本文推导的计算方法及前述测试参数，计算不同风速下的取样流量，并与实验测试的取样流量进行了比较，二者的相对偏差为

%

(18)

式中，Qc和Qe分别表示标准状态取样流量的计算值和实验值，m3· s-1。

取样流量的计算值和风洞实测值的相对偏差如图3所示。

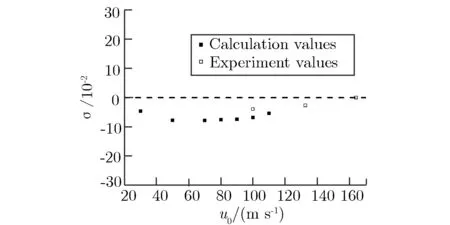
图3 取样流量的计算值和风洞实测值的相对偏差Fig.3 Relative bias of calculated sampling flow rates with the experimental ones in wind tunnels

从图3可以看出，在风速30～164 m· s-1内，计算结果与实验结果吻合，相对标准状态偏差在10%以内，高速风洞实验条件下的相对偏差在5%以内。偏差很可能来自式(11)的假设p1=p0。

虽然不可压缩流条件对应的气体流速范围大致在110 m· s-1以下，但对本文中的装置，从图3可以看出，风速u0达到近164 m· s-1时，前述计算方法仍然适用。主要原因可能是取样装置内的气体流速显著小于风速，表现为不可压缩性。

3 讨论

3.1 取样流量与平台行进速度的关系

由式(1)可知，冲压取样的动力主要来自平台与空气相对运动所产生的冲压，而冲压主要由空气的密度和行进速度决定。使用前述的计算方法，以u0为30 m· s-1时过滤装置的取样流量为基准换算为相对流量，线性相关系数R2= 0.999 2,计算了标准状态条件下的取样流量，如图4所示。

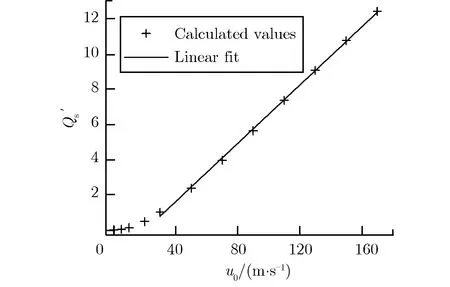
图4 计算的地面取样相对流量及拟合的直线 Fig.4 The calculated relative sampling flow rate and the fitted line

从图4可以看出，取样流量随平台行进速度先缓慢上升，然后呈线性增长。分析可知：随着速度u0的增加，冲压呈二次方增长，如式(1)所示。而取样压阻在较低过滤流速下成线性增加趋势，在较高流速下也近似呈二次方增加，如式(4)所示；当平台行进速度大于30 m· s-1时，冲压和压阻随来流速度变化的二次方关系相抵消，产生了线性关系。

3.2 海拔高度对取样流量的影响

大气温度、压力和空气密度均随海拔高度的变化而变化[12]，这些参数都会对取样流量产生影响。设定平台行进速度u0= 100 m· s-1，计算了不同海拔高度下的工况取样流量(即在取样温度、压力下的空气流量)和标准状态取样流量。图5给出了相对地面的取样流量随高度的变化及大气密度和大气压随高度变化的情况[12]。

图5 相对地面的工况取样流量Qv′、标准状态取样流量QS′、 大气密度ρ′和大气压p′(u0 = 100 m· s-1)随海拔高度的变化 Fig.5 Sampling flow rates, air density and air pressure at varied altitudes to those on the ground (u0 = 100 m· s-1)

从图5可以看出，随海拔高度的增加，相对工况取样流量Qv′略有减小，而相对标准状态下取样流量Qs′却显著减小。这种变化的主要原因是由于随海拔高度的增加，空气密度显著减小，取样冲压也随之减小，同时, 空气黏度小幅减小使得过滤压阻减小，过滤装置中气体流速略有减小，因此使相对工况取样流量Qv′略有减小；而相对标准状态下取样流量Qs′受空气密度影响较大，因此下降幅度较为明显。同时也注意到，相对标准状态下取样流量Qs′与相对大气压p′两条线近乎吻合，但从前述分析可以得出，二者应当并无必然联系，应当属于巧合。

4 结论

本文从机械能守恒原理出发，推导了不可压缩流条件下冲压过滤取样流量的计算公式，计算了30～164 m· s-1风速条件下的取样流量，并与风洞实验结果进行了对比，二者在10%以内符合，表明该计算方法是合理可信的。运用该计算方法讨论了平台行进速度和海拔高度对取样流量的影响。结果表明：在稳定大气条件下，平台行进速度较高的情况下，标准状态下取样流量随气体流速呈线性增加；随取样高度的增加，取样标准状态流量相对地面会有较大幅度减小。

[1]常印忠, 刘龙波, 王世联, 等. PMS-800大流量大气颗粒物采样器的研制[J]. 辐射防护, 2011, 31(1): 39-42. (CHANG Yin-zhong, LIU Long-bo, WANG Shi-lian, et al. Development of PMS-800 atmospheric particulate sampler[J]. Radiation Protection, 2011, 31(1): 39-42.)

[2]BUKOWIECKI N, DOMMEN J, PREVOT A S, et al. A mobile pollutant measurement laboratory-measuring gas phase and aerosol ambient concentrations with high spatial and temporal resolution[J]. Atmospheric Environment, 2002, 36(36/37): 5 569-5 579.

[3]WOOD R C. Direct-flow filter sampler: An improved large-volume collector of radioactive stratospheric debris [J]. J Appl Meteo,1964, 3(2): 194-197.

[4]杨吉纯, 李伟亮. TJ-1 型超声速取样器的气动设计与风洞试验[J]. 流体力学实验与测量, 1998, 12(1): 68-73. (YANG Ji-chun, LI Wei-liang. Aerodynamic design and wind tunnel test of a type TJ-1 supersonic sampler[J]. Experiments and Measurements in Fluid Mechanics, 1998, 12(1): 68-73.)

[5]LARSEN H C. Aerodynamic design considerations and wind-tunnel test of high-altitude air sampler[J]. J Spacecraft Rockets, 1967, 4(9): 1 254-1 261.

[6]徐宏坤, 吴其反, 程建平. 放射性气溶胶采样装置. CN103115802 B[P]. 2015-05-20.(XU Hong-kun, WU Qi-fan, CHEN Jian-ping. Radioactive aerosol sampling device. CN103115802 B[P]. 2015-05-20.)

[7]周光坰, 严宗毅, 许世雄. 流体力学[M]. 2 版. 北京: 高等教育出版社. (ZHOU Gong-jiong, YAN Zong-yi, XU Shi-xiong, et al. Fluid Mechanics[M]. 2nd ed. Beijing: Higher Education Press, 2000.)

[8]杨吉纯, 李伟亮, 陈敦厚, 等. 空中取样用几种过滤材料阻力特性及过滤效率的测定[J]. 原子能科学技术, 1997, 31(6): 519-523. (YANG Ji-chun, LI Wei-liang, CHEN Dun-hou, et al. Determination of resistance characteristic and efficiency of several filter materials for air sampling[J]. Atomic Energy Science and Technology, 1997, 31(6): 519-523.)

[9] HINDS W C. Aerosol Technology: Properties, Behavior and Measurement of Airborne Particles[M]. New York: John Wiley & Sons, Inc., 1999.

[10] 陈敏恒, 丛德兹, 方图南, 等. 化工原理[M]. 2 版. 北京: 化学工业出版社, 1999: 122. (CHEN Min-heng, CONG De-zi, FANG Tu-nan, et al. Principles of Chemical Industrial[M]. 2nd ed. Beijing: Chemical Industrial Press, 1999:122.)

[11] BARON P A, WILLEKE K. Aerosol Measurement: Principles, Techniques, and Applications[M]. New York: John Wiley & Sons, Inc., 2001.

[12] 国家标准总局. 标准大气(30公里以下部分)[S]. GB 1920-80,1980. (SAC. Standard Atmosphere(Below 30 kilometers)[S]. GB 1920-80,1980.)