基于自适应人工蜂群算法优化的最小二乘支持向量机在变形预测中的应用

冯腾飞， 钟钰， 刘小生， 于良

（江西理工大学建筑与测绘工程学院，江西 赣州341000）

针对目前生活中各种变形体如滑坡、基坑等由于发生变形给社会带来的危害，如何对变形体的变形趋势做出准确预测并及时提出预警是急需要解决的问题.比较熟知的预测方法有回归分析法、灰色理论、神经网络、支持向量机[1]等.支持向量回归机（Support Vector Regression，简称 SVR）是 20 世纪90年代由贝尔实验室Vapnik提出的一种能够处理回归和模式识别等诸多问题的新型统计学方法[2-3].最小二乘支持向量回归机（Least Square Support Vector Regression，简称 LSSVR）是SVR的扩展，它不仅继承了SVR的优点，即它能很好地解决数据量少、过学习、局部极小点等实际难点，具有很强的泛化能力，而且LSSVR将SVR中的二次规划问题转化为求解线性方程组的问题，简化了计算，所以LSSVR作为一种新型的机器学习方法已经被应用到变形预测领域中.但是继承了SVR优点的同时，LSSVR也面临着惩罚参数和核函数参数σ难以取值的问题，参数的优化将会直接决定LSSVR的拟合精度和泛化性能.常用的参数优化方法主要包括网格搜索法[4]、交叉验证法[5]、直接确定法等.但这些参数优化方法均存在各自的缺点[6]：如网格搜索法并不一定能得到最优参数且计算量大；交叉验证法同样需要大量计算且耗时长，不适用于实际生产；直接确定法要求有较高的先验知识.人工蜂群算法（Artificial Bee Colony， 简称ABC） 是 Karaboga在2005年提出的一种模拟蜂群协作寻找蜜源的生物智能优化算法[7]，ABC具有参数设置少、计算简单、更大概率得到最优解等诸多优点，文献[8]在分析比较了多种优化算法后，得到了ABC是性能最好的几种优化算法之一这一结论.但是受制于搜索结构的限制，ABC存在搜索精度不高以及早熟收敛等缺点.

针对ABC算法的不足，文章结合蜜蜂的觅食行为及实际需要，提出一种自适应人工蜂群算法（Adaption ABC，简称AABC）.对于蜜源搜索策略，设计了一种新的步长更新算子自适应调整蜂群的搜索方向及搜索范围；对于蜜源选择概率，引入反向轮盘赌选择机制，并设计了新的自适应选择算子将轮盘赌和反向轮盘赌结合起来，以此平衡标准ABC的勘探和开发能力，提高标准ABC的参数寻优性能.利用AABC优化LSSVR的惩罚参数和核函数参数，通过参数优化后的LSSVR建立变形预测模型，并将此模型应用于某滑坡变形预测.

1 基本理论简介

1.1 最小二乘支持向量回归机

LSSVR基本思想[9-10]就是利用已知的样本数据得出一个最佳拟合函数，根据这个函数再输入新的样本数据，从而计算出对应的输出值.其具体步骤为：

给定训练集：

其中，xi∈Rn，yi∈Y=R，i=1，…，l.用非线性映射将样本输入映射到高维空间，构造出LSSVR的函数为：

其中，ω为权值向量，b为偏差.将之转化为下列优化问题：

其中，c为惩罚参数，ξi≥0为松弛因子.利用Lagrange函数和KKT优化条件可解得LSSVR的函数模型为：

其中，ai是 Lagrange 乘子，K（x，xi）是核函数.

变形预测模型需较强的拟合能力，故文中采用Gauss径向基函数[11]作为LSSVR的核函数：

1.2 标准人工蜂群算法

标准ABC是根据蜜蜂采蜜的整个过程模拟出的一种智能算法，根据分工的不同种群可分为引领蜂、跟随蜂和侦查蜂，引领蜂和跟随蜂各占整个蜂群规模的一半，蜜蜂在寻找食物源的过程可以被抽象成寻找问题最优解的过程[12]，3种蜜蜂各司其职，以协同的方式高效完成寻优工作.其寻优原理[13]如下：

设蜜源 xi（i=1，2，…，NP），xi的质量对应于解的适应度值fit，设求解问题的维数为D，迭代次数为t，最大迭代次数为T，则t次迭代时蜜源位置为，即搜索空间的上下限.

1）随机产生蜜源的初始位置：

2）在初始蜜源的周围搜索产生一个新的蜜源：

其中，j=1，2，…，NP 且 j≠i.φ 是[-1,1]均匀分布的随机数.

3）评价两个蜜源的适应度，根据贪婪算法确定保留xi或vi.

fi为解的函数值.

4）计算引领蜂找到的蜜源被跟随的概率：

5）跟随蜂采用轮盘赌的方式选择引领蜂，即在[0,1]内产生均匀分布的随机数 r，当 Pi＞r，则跟随蜂在蜜源i周围产生一个新蜜源，利用贪婪算法确定保留的蜜源.判断蜜源是否满足被放弃：经t次迭代到达阈值limit仍没找到更好的蜜源，则放弃.

6）放弃：引领蜂变为侦查蜂，在搜索空间随机产生一个新蜜源代替xi：

7）不放弃：t=t+1，判断算法是否达到终止条件，输出最优解.

2 自适应人工蜂群算法

2.1 自适应步长更新

对蜜源搜索策略公式（6）分析：种群的搜索范围及搜索精度由步长φ控制，但φ的取值完全是随机的，当φ取值过大时，容易跳出真正的全局最优解；当φ取值过小时，容易提早收敛，得到局部最优解.根据对蜜蜂觅食行为的分析，在搜索前期应该有较大的搜索步长，以便快速向全局最优解周围聚集，提高收敛速度；在搜索后期，算法搜索得到的最优解已经靠近真实的最优解，此时应该逐渐减小搜索步长来实现对最优解周围的细化搜索.因此，设计了一种自适应递减算子来更新搜索策略的步长：

其中，φ0∈（0，1），t={1，2，…，T}

2.2 自适应选择概率

在标准ABC算法中只选择适应度高的蜜源，适应度低的蜜源被迅速淘汰，这无疑会导致种群的多样性下降，很难达到全局最优.因此，文中引进文献[14]中反向轮盘赌选择机制，并将轮盘赌和反向轮盘赌结合起来，设计了一种新的自适应概率选择机制：

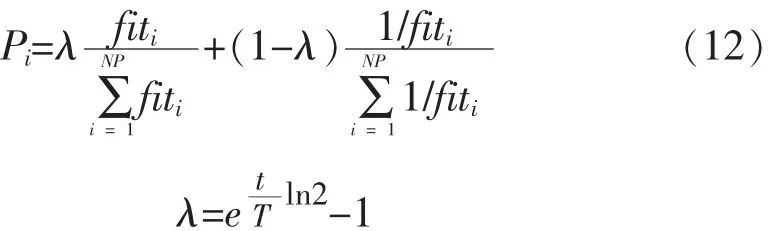
其中，λ∈（0，1）.算法前期，→0，λ→0，此时选择概率为反向轮盘赌选择机制，说明适应度差的蜜源也有被挑选的可能，提高了算法的求泛能力，保证了多样性；算法后期，→1，λ→1，此时选择概率为轮盘赌选择机制，算法只选择适应度高的蜜源，加快了收敛速度和收敛精度.所以整个选择过程通过自适应函数在求泛与求精中调整.

3 基于AABC优化LSSVR的预测模型构建

将自适应步长更新公式（11）及自适应蜜源选择公式（12）分别替代原始ABC算法中的公式（7）和公式（9）即得到AABC算法，将AABC与LSSVR相结合，用于变形预测模型的构建，其具体步骤如下：

1）对变形监测数据进行预处理：归一化计算：

2）设置AABC的参数：蜂群数量NP，蜜源最大搜索次数limit，算法最大迭代次数T，蜜源的维度即待优化参数的个数D及各参数的取值范围；

3）选定目标函数：将LSSVR拟合出的最小均方根误差RMSE作为AABC算法的目标函数，并将之转化为适应度函数：

4）将公式（11）替代公式（7），公式（12）替代公式（9）得到AABC算法；

5）利用AABC算法优化LSSVR各参数得到LSSVR的最优参数解；

6）输出待预测的值.

4 工程实例

以文献[15]中实验数据为例，某滑坡体为土质滑坡，有多条裂缝贯穿该滑坡体，其变形主要受降水量及温度影响，其中ZG118监测点的水平位移监测资料共包含21期数据，监测时间段为2004年4月至2005年12月，监测频率为每月测量一次.先对全部数据进行去噪处理，保证原始数据不再包含粗差，再将前18期数据用来建立预测模型，后3期数据用于模型预测效果对比.

将AABC与ABC的参数设为一致：人工蜂群规模NP=20，蜜源数量是蜂群规模的一半，求解问题的维数D=2，最大迭代次数T=100，最大搜索次数limit=50，惩罚参数c和核函数参数σ取值范围为 （0.01,100）.根据 AABC_LSSVR 及 ABC_LSSVR的建模步骤编写matlab程序，可分别得到其各自预测进化对比图如图1所示.网格优化的LSSVR模型（G_LSSVR）也是比较流行的预测模型，为验证AABC_LSSVR模型的预测效果，用它与G_LSSVR模型以及ABC_LSSVR模型同时预测并进行精度比较，将前18期数据代入各模型进行拟合，得前18期数据拟合如图3所示，后3期预测结果如表1所示及预测趋势如图2所示.

根据图1可知，标准ABC在10代以内便直接达到收敛值，而AABC受自适应调节的控制，在前期，迭代曲线迅速下降，说明种群的迭代步长较大，收敛速度快；在中期，迭代曲线处于平稳状态，说明保留了部分适应度低的蜜源，使种群多样性得到补充；在后期，迭代曲线再次迅速下降达到收敛值，说明此时只挑选了适应度高的蜜源.对比AABC与ABC的收敛值可知，AABC的收敛精度更高，由此可知，AABC得到了更优的参数组合.

根据表2中各模型对后三期的预测结果可知，ABC_LSSVR模型、G_LSSVR模型以及AABC_LSSVR模型预测的平均相对误差分别为2.24%、2.27%及1.77%，可见AABC_LSSVR模型的预测精度最高.再根据图2图3所示，AABC_LSSVR模型预测的变形量曲线与观测变形值曲线更为吻合，更能反映变形的趋势.

表1 各模型预测结果

图1 AABC_LSSVR与ABC_LSSVR预测进化图

图2 各模型预测结果

图3 AABC_LSSVR模型拟合结果

5 结 论

针对标准ABC的不足，文中设计了自适应步长搜索公式和自适应概率选择公式来平衡标准ABC的勘探和开发能力，以此提出了AABC算法，并结合LSSVR构建了AABC_LSSVR变形预测模型，将此模型应用于滑坡预测，结果表明，相比于ABC_LSSVR模型和G_LSSVR模型，AABC_LSSVR模型预测精度更高，预测趋势更贴合实际，具有一定的实用价值.

[1]毛伊敏，周昭飞，彭喆，等.基于不确定多分类支持向量机在滑坡危险性预测的应用[J].江西理工大学学报，2016，37(3):102-108.

[2]Vapnik V.The nature of statistical learning theory[M].Springer Science&Business Media,2013.

[3]陈祖云，张桂珍，邬长福，等.支持向量机在矿井突水水源识别中的应用[J].江西理工大学学报，2009，30(5):10-13.

[4]曲健,陈红岩,刘文贞,等.基于改进网格搜索法的支持向量机在气体定量分析中的应用[J].传感技术学报,2015，28(5):774-778.

[5]谢宏，魏江平，刘鹤立.短期负荷预测中支持向量机模型的参数选取和优化方法[J].中国电机工程学报，2006，26(22):17-22.

[6]高雷阜，高晶，赵世杰.人工蜂群算法优化SVR的预测模型[J].计算机工程与应用，2016，52(11):55-59.

[7]林凯，陈国初，张鑫.多交互式人工蜂群算法及其收敛性分析[J].计算机应用，2017，37(3):760-765.

[8]Pholdee N,Bureerat S.Comparative performance of meta-heuristic algorithms for mass minimisation oftrusses with dynamic constraints[J].Advances in Engineering Software,2014,75(9):1-13.

[9]任超，梁月吉，庞光锋，等.基于灰色最小二乘支持向量机的大坝变形预测[J].大地测量与地球动力学，2015，35(4):608-612.

[10]王奉伟，周世健，周清，等.局部均值分解与支持向量回归的大坝变形预测[J].测绘科学，2016，41(10):132-135.

[11]张敏，肖海波.SVM算法在入侵检测中的应用[J].江西理工大学学报，2007,28(3):39-40.

[12]韩建权，毛力，周长喜.基于改进局部搜索策略的人工蜂群算法[J].计算机科学与探索，2015，9(6):761-767.

[13]秦全德，程适，李丽，等.人工蜂群算法研究综述[J].智能系统学报，2014，9(2):127-135.

[14]冷昕，张树群，雷兆宜.改进的人工蜂群算法在神经网络中的应用[J].计算机工程与应用，2016，52(11):7-10.

[15]陆付民，蒋廷耀.基于多因子及泰勒级数的滑坡变形预测模型研究[J].大地测量与地球动力学，2017，37(10):1029-1032.