关于非线性激活函数的深度学习分类方法研究
杨国亮, 许楠, 李放, 龚曼
(江西理工大学电气工程与自动化学院,江西 赣州 341000)
在过去几年中,计算机视觉发展迅速,出现了如阈值处理[1]等先进的技术.已经从工程特征体系发展至端到端特征学习架构,如深层神经网络,以及其在语义分割[2]和图像检索[3]上的应用.产生这种革命性变化的主要原因是大数据集、高性能硬件和新的有效模型等的迅速发展.其中,最关键的一个因素是激活函数对深层无监督学习的影响.
人工神经网络利用激活函数的历史早于深度学习,从初始的S型函数 (Sigmod)、正切函数(tanh)到已知的目前应用最广泛的整流线性函数(ReLU)[4].而ReLU的出现使得深层神经网络的训练水平取得了新的突破.ReLU是一个分段线性函数,可将负输入保持为正输入,输出为零.这种形式使得它可以减轻梯度消失的问题,适合训练深层神经网络.然而,它也有一个潜在的缺点,即一旦梯度达到零,神经元将永远不会激活.针对这一缺陷,Maas 等[5]提出了漏整流线性单元(LReLU),将ReLU的零负部以线性函数代替.其后,LReLU被扩展为参数整流线性单元(PReLU)[6],将负部的斜率改为由参数α控制,通过神经网络的反向传递不断更新修正α的值,这一想法是突破性的,改变了以往激活函数没有学习能力的性质.实践表明PReLU能够实现更高的分类精度,并且几乎不会出现因引入参数而引起过拟合的现象.在这之后,Clevert等[7]提出了指数线性单元(ELU),创新性地将负部的线性利用指数函数修正为非线性,使得负部具有了软饱和特性,导致更深入的学习和更好的泛化性能,但是其参数无法反向更新.上述的两类激活单元在最新的深度学习框架中已经能够直接调用,达到了公认的效果.但是,指数单元和整流单元之间存在一种隔阂,致使其相互之间不具有统一性.整流单元只能够很好地表达线性函数簇,而指数单元只能够表达非线性指数函数簇,这些缺陷在某种程度上可能会破坏只能使用特定的激活函数的架构的代表性能力.此外,大量研究表明,ELU与批次归一化(Batch Normalization,BN)[8]结合使用可能会损害分类精度.目前,使用BN是非常深的网络消除过拟合风险的主要手段之一.
针对以上所述激活函数的优缺点,由PReLU和ELU启发,提出了一种新的激活单元.它相对于PReLU和ELU而言拥有更多参数,能够涵盖现有的整流单元和指数单元,并且能够在二者之间互相转换.另外,函数正部分被做出了修改,其线性条件被修正为非线性,这可以实现在几乎不影响训练精度的情况下适当加快收敛速度的目标.
1 非线性指数单元
非线性指数单元 (Non-Linear Exponential Unit,NLEU)根本上是ELU的泛化,即它本身来源于ELU,具有ELU的所有优点,但其又不同于ELU.对于负部分,为了弥合ELU和PReLU的差异,在ELU的基础上加入额外的参数β,以控制ELU的形状变化.再者,ELU的参数值只能人为的调节而不具有反向自动调整的能力,但NLEU则解决了这一不足;对于正部分,增加参数η使其线性转化为指数非线性,不同于Sigmod和tanh函数可能会导致梯度消失,NLEU不会出现此现象.因为其不具有右饱和性质,其导数不会趋近于0.通过反向传递随机梯度下降算法(SGD)优化参数β、α和η,使之能够在指数单元、整流单元之间随意切换.这种设计使NLEU比其前身ReLU、PReLU和ELU更加灵活,而后者均可视为NLEU的特殊情况.因此,通过学习参数α、β和η,负部分的线性和非线性空间可以在单个激活功能模块中被覆盖,正部分亦可调节覆盖范围,而其它激活则不具有此属性.
公式 (1)~(3) 分别为激活 ReLU、PReLU 和ELU的公式表达式.

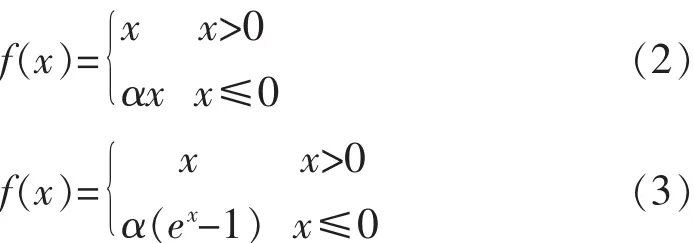
由公式(1)可见,ReLU 在 x<0时硬饱和,因此具有负部稀疏性;在x>0时导数恒为1,从而保证ReLU保持梯度不衰减,进而缓解梯度消失问题.而PReLU引入可学习参数α调节负部斜率,并通过反向带动量方式[6]不断更新,利用通道策略解决增加参数所带来的过拟合风险.ELU总结了整流单元的优点与不足,提出将负部修正为指数函数,具有左侧软饱和特性,它的总体输出均值接近于零,所以收敛速度更快.
以上三种激活方式对深度神经网络的发展产生巨大影响.但是正如引言所述,经过仔细分析后发现:指数单元与整流单元存在一种共性但缺乏理论上的统一.为此,提出了非线性指数单元,其形式上属于指数单元但可以对整流单元全覆盖.通过调整参数α、β的值可以实现在PReLU、ReLU和ELU之间的随意转换.如公式(4).

进一步,将公式(4)的正部分引入参数η修正为指数函数,以缩减正部分均值,实现更好的总体均值,其梯度不再恒定为1,而是随着训练的不断深入逐渐降低.这并不用担心梯度消失的问题,因为它与Simgod和tanh不同,并不具有右饱和.通过对参数η的调节可以恢复为线性,提高了NLEU的覆盖域调节能力.最终得出非线性指数单元的基本公式,如公式(5).ReLU、PReL、ELU 及 NLEU的函数图像如图1所示.值得注意的是,参数η的初始值理论上应当在0~1之间接近于1的范围内调节,才能具有在几乎不影响训练精度的情况下适当提高收敛速度的作用.若超过1则会使梯度不断上升从而导致可能的发散;如果远离1而接近于0,则会导致正部分信息的大量流失,使得训练精度急速下降,在学习率较大的情况下,致使过拟合的出现.同理,负部在不具有同ReLU类似的稀疏能力的情况下,参数α和β的设置使得NLEU负部范围的变化也可能会导致网络在训练到一定程度时发散.理论上讲,上述可能的情况并不是由增加参数所带来的,因为这些现象都能通过调节参数值而得到解决.在实验部分将有具体分析以证明以上理论的正确性.
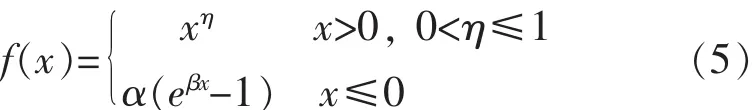
由公式(5)可见,当η=1时,NLEU正部分退化为线性x;当β=1时,NLEU负部分退化为ELU;当β固定为很小的值时,负部分近似为PReLU;当α=0时,负部等价于ReLU.

图1 4种激活函数图像
对于NLEU来说,其参数α、β和η的值通过类似于权重反向更新的方式更新.由于NLEU处处可微,因此使用NLEU的深度网络可以端到端地训练.公式(6)为NLEU的参数更新法则,其中求偏导表示所对应参数的梯度.

对于参数更新而言,其初始值显得不是很重要,但是参数初始化对于结果的影响是不可忽略的.根据前者的理论基础[6-7],对于α,一般选用0.25、1或2为初始值进行设置;对于β,选用1进行初始化;对于η,在1~0之间以0.05为间距逐步取值作为其初始值.在实验中,将分析各参数不同初始值对结果的影响.另外,文中强调了激活函数参数更新的权重衰减的重要性,这不同于整流单元,权重衰减对于指数单元的影响不可忽略.
此外,受到ELU不能使用BN的启发,增加了额外参数的NLEU,理论上能够使用BN,这也大大提高了NLEU在更加深层的网络中的优化能力.在不考虑正部分非线性的情况下,NLEU可以固有的分为如公式(7)所示的结构.训练时,数据信息流出BN后首先流入类似PReLU形式中,而PReLU对BN有效,所以能够显著提高激活性能.这种结构使得NLEU拥有了良好的融合性能.在公式(7)的基础上,再引入对正部分的非线性控制以使此函数的结构完整.
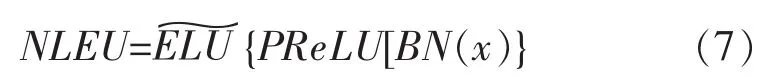
增加参数也带来了可能出现的过拟合风险.由于其参数更新与卷积权重更新方法相类似,所以采用了与PReLU相似的方法——多参数共享通道策略来解决可能的风险.对于网络中众多的权重数而言,增加的参数与权重共享通道后对结果的影响很小.在训练几十万以上的大数据的情况下,出现过拟合的可能性更低.在实验中可以发现,只要参数值设置合理,则并不会导致过度拟合.值得一提的是,增加参数所导致的计算量的增加可能会导致训练时间的大幅增加.通过仔细的优化代码,最终的训练结果显示,采用NLEU的网络与采用PReLU的网络用时近似,有略微增加.
2 实 验
为了验证NLEU在不同网络结构和不同数据库下的实际效果,利用深度学习框架Caffe[9]分别在Cifar10和Cifar100数据集上做了具体实验.这些实验针对最先进的架构、深浅不同的网络以及不同的激活函数.本节具体介绍了每项实验的实现过程,并对结果进行分析以验证所提出的理论.另外,文中复现了不同先进架构的训练过程,并通过改进其激活函数,能够实现更为先进的结果,这能够证明NLEU的有效性.以下所有实验,NLEU中的参数α的初始值设置为0.25、1或2;对于参数β,选用1进行初始化;而η的初始值则根据每项实验的实际需要进行调整.在此声明,文中所有实验结果均取五次实验中的最优结果登记.
2.1 在Cifar10数据库的实验
本实验初步验证NLEU的效果.采用NIN(NetworkinNetwork)[10]架构和密集卷积网络DenseNet[11]在Cifar10数据库上分别进行实验.首先,NIN架构有9个卷积层,其中6个具有大小为1×1的内核,且该架构没有完全连接(FC)层,易于训练,足以综合评估可学习参数的作用.其次,密集卷积网络是最新的CNN分类架构,可以验证NLEU在先进架构中的效果.Cifar10数据库包含50000个大小为32×32的训练样本和10000个同大小的验证样本,共分为10类.
在使用NIN架构进行试验时,每组实验除激活层外网络其他部分均保持相同.以整流单元ReLU、PReLU和指数单元ELU为具体的函数变量.网络采用高斯初始化,对应标准差为0.05,共进行120000次迭代计算.激活参数权值更新不使用衰减策略,试验时改变的仅仅是参数初始值.学习率衰减方式可分为单步衰减和多步衰减方式.另外,文中复现了文献[10]中NIN架构在原始Cifar10数据集上的实验,精度为89.72%(如表1中ReLU结果),原文为89.59%,结果近似.表1显示了具体实验结果.

表1 在Cifar10数据库上的实验结果
当激活函数变为NLEU,且α的初始值设置为0.25和1并采用单步学习率衰减方式时,出现未迭代至100000次(该处为学习率第一次进行衰减)便发散的情况.而使用其他激活函数并没有出现这种情况.当然,这种现象是在初始学习率设置为0.01的情况下出现的,将初始学习率减小10倍后,该现象消失,但训练结果明显变差.为此,增设一组对比实验,即多步学习率衰减实验,即提前进行学习率的衰减,迭代至100000次后再衰减一次.经过对实验过程的分析观察发现,当缩小η的值时,发散的情况会愈加严重,即会缩短发散出现的迭代次数.而如果增大α的初始值,则这种状况会逐渐减轻,当α增大到2时,这种现象完全消失.该现象的出现,原因可能是由于缩小正部范围会导致部分正信息流失,从而加速了发散的出现.而增加负部分的区域,则会导致负信息尽可能地被包括而减少信息流失.二者均从总体输出均值接近零的方面来考虑,因而缓解了发散的出现.但并非负部区域越大结果越好,当α初始值被增加到3时,与α=2相比,结果并无明显差距,说明当α增大到一定值后,即负部信息被尽可能的包含后,再做出增大α初始值的行为便无效.上述分析说明,这种状况的出现并非是由于增加参数而导致,因为此现象可以通过调节参数而得到解决.
对表1数据分析可知,当使用多步学习率衰减时,NLEU展示了绝对的优势,这恰恰证明了NLEU具有在学习率较小的情况下,能够取得较高精度的优点.当α增大至2时,与ELU、ReLU及PReLU相比具有明显的优势,ENLU-NIN所取得的92.15%的训练精度显著优于文献[10]中89.59%的精度.以上结果表明了增加参数所带来的好处.另外,参数η的小幅度减小并未对结果造成很大影响,如果是在对精度要求较小的情况下,便可通过调节η加快收敛速度.经过对不同η初始值的训练日志分析后发现,当η=1时,在102000次迭代后精度达到0.9,而η=0.95时则在96000次达到该精度,η=0.85时则在76000次,在η=0.8时更是在62000次达到0.9的精度.这种调整和所带来的现象在本实验中显得没有必要,但是在百万级甚至上亿级的数据训练之中显得不可忽略.从表1中还可以发现,ELU的参数初始值的变化对结果的影响几乎可以忽略不计,而NLEU则完全相反.图2为ReLU、PReLU、ELU和NLEU最优的精度和对应的训练损失变化曲线.

图2 NIN架构在Cifar10上使用不同激活的最好结果

图3 NLEU在密集卷积架构中的实验变化曲线
从图2中可以发现,NLEU能够在收敛速度和训练精度上对其他激活方式取得双重优势.
随后,文中使用40层DenseNet架构进行了验证实验.在使用NLEU改进网络后得到的精度为92.64%,优于原始架构复现得到92.26%.这说明NLEU能够一定程度上改善网络,证明了NLEU优秀的普遍性,其在先进架构中仍然能够发挥优势.图3显示了密集卷积网络原始结构、以NLEU有激活权值衰减方式改进和无激活权值方式改进后的训练损失和测试精度变化曲线.
从图3可以看出当有激活参数权值衰减时,NLEU略优于原始密集卷积架构.当无激活参数权重衰减时与前两者有较大差距,权重衰减所导致的结果刚好与实验2.2中使用MNIN架构相反,这里可能和架构的组织有关.尽管如此,NLEU仍然保持优势.
2.2 在Cifar100数据集中的实验
为了实现更好的结果,首先改进了NIN架构,使之能够实现更高的准确率.改进措施主要是:在原始架构上增加了一个NIN单元;增加了原网络没有的全连接层;将第一个池化层改为平均池化;为了解决增加层数所带来的损失,网络增加了“退出(Dropout)”[12]单元,并根据数十次的实验结果优化了卷积参数;为了与激活更好的搭配,将卷积权重初始化方法改为 “Xavier”[13]初始化方法.最终使网络结构达到13层,将其命名为“MNIN”架构,并声明所做的所有改进都是以实验结果为依据,以便实现更好的效果和验证NLEU.采用MNIN架构训练Cifar100(共100类,50000训练样本和10000验证样本),主要针对不同激活、权重衰减与否以及不同参数的变化三个方面验证NLEU对于多分类任务的表现.实验分别在60000、90000次迭代后使学习率衰减一次,基础学习率为0.01,其他设置基本与实验2.1相同.值得注意的是,为了保证精度,在实验2.2和实验2.3当中,参数η均被设置为1且不更新.结果发现,MNIN较NIN架构在各种情况下的准确率普遍有了较为明显的提升.表2显示了具体的实验结果.

表2 MNIN架构在Cifar100上的结果
通过表2发现,NLEU具有一致的优越性.结果显示,激活参数的权重衰减与否会影响最终的分类效果.与实验2.1及2.3结果相联系可以发现,激活参数的权重衰减对于分类精度的影响可能是积极的也可能是消极的,具体的原因缺乏理论解释.尽管这种影响在某些情况下表现的很微弱,但是仍然可以显现.图4显示了使用不同激活函数的MNIN架构的准确率及对应训练损失变化曲线.从图中可以发现NLEU的训练情况略优于ELU,明显优于PReLU和ReLU.
另外,文中使用NLEU并采用前面实验效果最优的参数设置改进了宽泛残留架构(Wide Residual Networks,WRN)[14],以训练原始 Cifar100 数据集,最终实现了非常先进的结果.表3显示了与其他经典架构的对比.
2.3 经典残差网络(ResNet)实验
为了验证BN对NLEU的影响以及该函数在深层网络中的效果,使用不同层数的残差网络训练原始Cifar10数据库.此实验使用了与文献 [20]一致的非瓶颈残差结构.为了提高实验的可靠性,首先复现文献[20]中相关实验.经对比,结果与原文近似.求解文件设置10万次迭代,初始学习率为0.1.表 4、表5、表6分别为20层、32层及56层残差网络实验结果.
由表4可以看出NLEU在有权值衰减时对其它激活保持精度上的优势,在α=0.25时达到最佳.尽管这种优势是微弱的,但这是在小数据集上的结果,如果在大数据集上可能会实现更明显的优势.
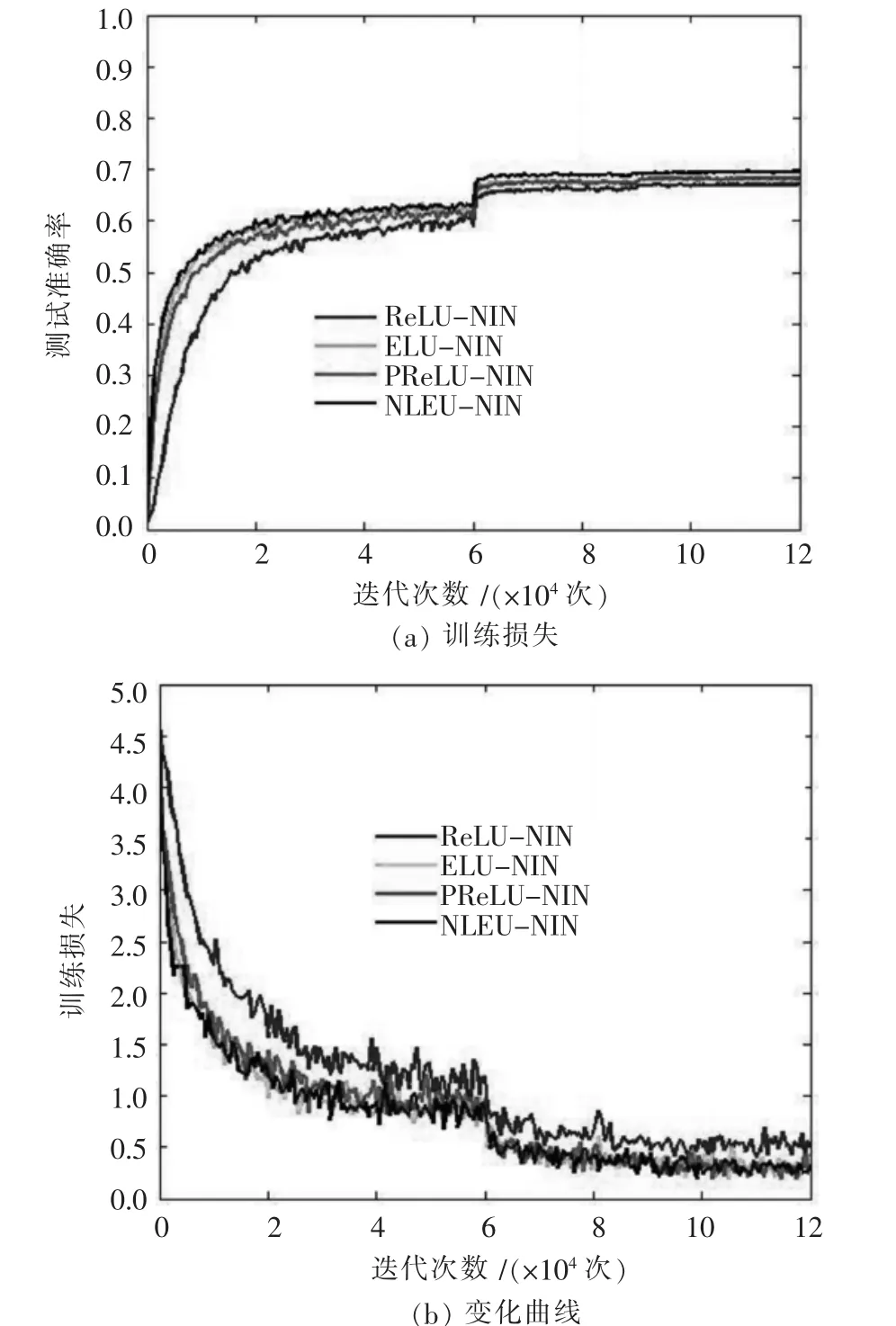
图4 架构MNIN在Cifar100上不同激活的准确率
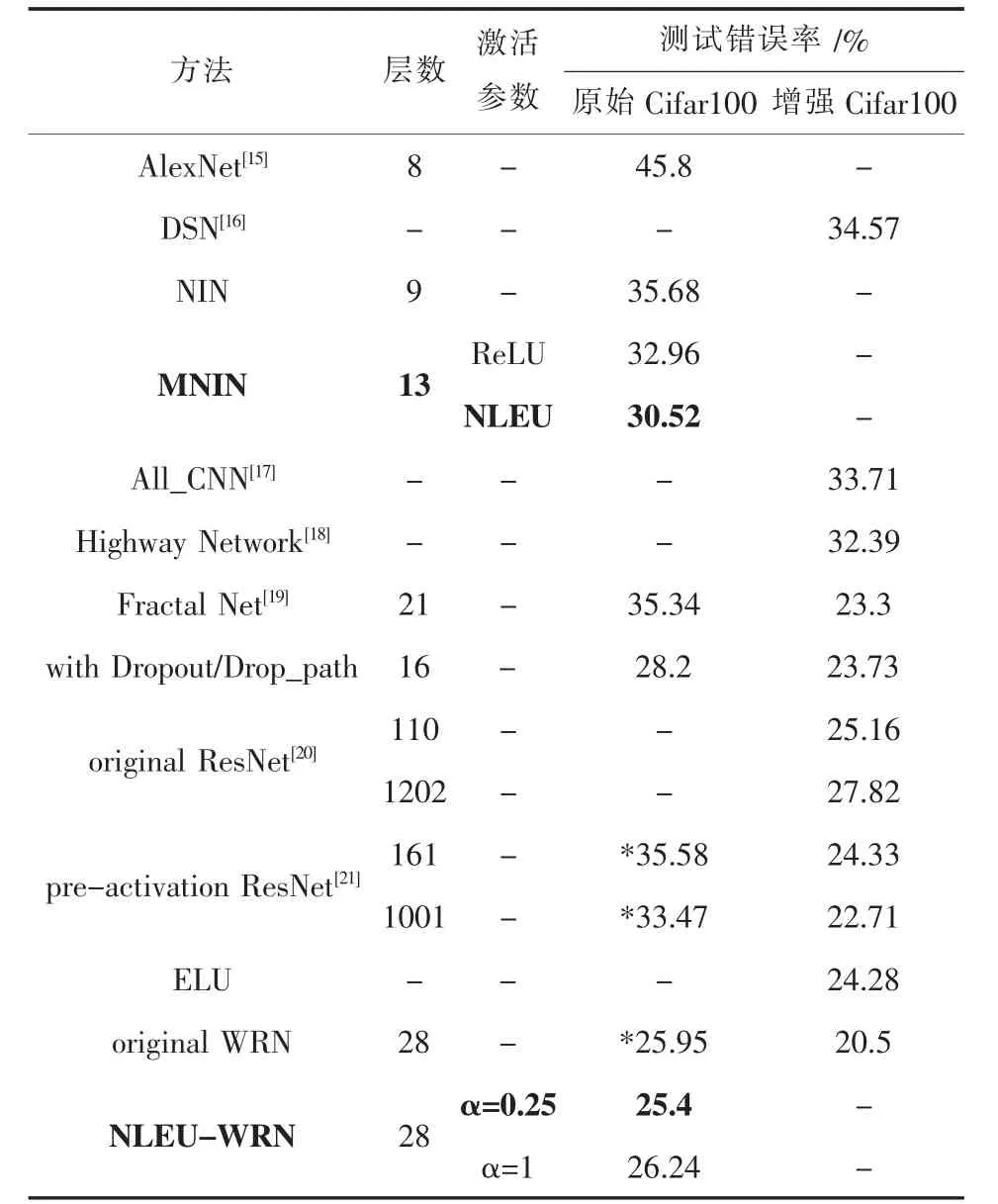
表3 NLEU-WRN与经典架构的结果对比

表4 20层ResNet实验结果

表6 56层ResNet实验结果

表5 32层ResNet实验结果
经过实验可以看出,深层ResNet(56层)的精度相比于32层并无明显优势,潜在的原因可能是深层非瓶颈结构对训练会产生不利的影响.这也是文献[20-22]在56层以上的深层网络中更多地采用瓶颈结构来训练的原因.同时发现,在网络中对卷积采用不同的初始化,并配合不同的激活会有不同的效果.
相比于本实验中的其它结果,只是简单地改变激活功能使得NLEU始终保持优势,通过调节参数初始值可以实现最佳的效果.在实验过程中发现,由于NLEU拥有参数可更新的性质,文中尝试在NLEU后添加BN层训练,结果发现无法训练,证明了激活层不同于卷积,BN对于参数可更新的激活函数并无益处.虽然在原始ResNet(该网络中每个卷积层后均使用了BN)中仅更改激活部分证明了BN对于NLEU激活并无害处,但那仅限于对卷积使用BN.
根据所有实验结果表明:在不同网络和不同数据集下使用NLEU取得最优的结果所对应的参数初始值的设置不同.另外,从本节表中可以发现,随着ResNet层数的增加,BN对ELU的影响越来越大.ELU在20层时优于ReLU,但在56层时效果已明显较差.总之,本实验证明了BN对NLEU无害.
3 结 论
激活函数是深层神经网络的重要组成部分,对特征提取的结果具有重大影响.文章推广了一种新的非线性指数激活函数,以应用在深度学习分类中.通过使用经典及最新的先进架构来进行试验,结果有力地证明了所提出的理论.另外,对NLEU在不同参数下的表现以及对其是否进行权值衰减所造成的影响做了分析.所有的实验结果表明:NLEU能够为深层网络的融合带来好处,在合适的情况下能够改善神经网络的性能,为今后神经网络的发展提供一个进步的方法.文中只专注了NLEU在深度学习分类任务中的作用,经后的研究工作应当是对该激活功能进行进一步优化,以实现更优的效果,进而将其推广应用到分割、检测等其他任务.
[1]杨国亮,鲁海荣,唐俊,等.基于迭代对数阈值的加权RPCA非局部图像去噪[J].江西理工大学学报,2016,37(1):57-62.
[2]Long J,Shelhamer E,Darrell T.Fully convolutional networks for semantic segmentation[C]//Proceedings of the IEEE conference on computer vision and pattern recognition.2015:3431-3440.
[3]Li Z,Tang J.Weakly supervised deep metric learning for community-contributed image retrieval[J].IEEE Transactions on Multimedia,2015,17(11):1989-1999.
[4]Glorot X,Bordes A,Bengio Y.Deep sparse rectifier neural networks[C]//Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics,2011:315-323.
[5]Maas A L,Hannun A Y,Ng A Y.Rectifier nonlinearities improve neural network acoustic models[C]//Proc.icml.2013,30(1):3.
[6]He K,Zhang X,Ren S,et al.Delving deep into rectifiers:Surpassing human-level performance on imagenet classification[C]//Proceedings of the IEEE International Conference on Computer Vision,2015:1026-1034.
[7]Clevert D A,Unterthiner T,Hochreiter S.Fast and accurate deep network learning by exponentiallinear units (elus)[J].arXiv preprint arXiv:1511.07289,2015.
[8]Ioffe S,Szegedy C.Batch normalization:Accelerating deep network training by reducing internal covariate shift[J].arXiv preprint arXiv:1502.03167,2015.
[9]赵永科.深度学习21天实战Caffe[M].北京:电子工业出版社,2016.
[10]Lin M,Chen Q,Yan S.Network in network[J].arXiv preprint arXiv:1312.4400,2013.
[11]Huang G,Liu Z,Weinberger K Q,et al.Densely connected convolutional networks[C]//Proceedings of the IEEE conference on computer vision and pattern recognition,2017,1(2):3.
[12]Hinton G E,Srivastava N,Krizhevsky A,et al.Improving neural networks by preventing co-adaptation of feature detectors[J].arXiv preprint arXiv:1207.0580,2012.
[13]Glorot X,Bengio Y.Understanding the difficulty of training deep feedforward neural networks[J].Journal of Machine Learning Research,2010(9):249-256.
[14]Zagoruyko S,Komodakis N.Wide Residual Networks[C]//British Machine Vision Conference,2016:87.
[15]Krizhevsky A,Sutskever I,Hinton G E.ImageNet classification with deepconvolutionalneuralnetworks[C]//International Conference on Neural Information Processing Systems.Curran Associates Inc.2012:1097-1105.
[16]Lee C Y,Xie S,Gallagher P,et al.Deeply-supervised nets[C]//Artificial Intelligence and Statistics,2015:562-570.
[17]Springenberg J T,Dosovitskiy A,Brox T,et al.Striving for simplicity:The all convolutional net[J].arXiv preprint arXiv:1412.6806,2014.
[18]Srivastava R K,Greff K,Schmidhuber J.Training very deep networks[C]//Advances in Neural Information Processing Systems,2015:2377-2385.
[19]Romero A,Ballas N,Kahou S E,et al.Fitnets:Hints for thin deep nets[J].arXiv preprint arXiv:1412.6550,2014.
[20]He K,Zhang X,Ren S,et al.Deep residual learning for image recognition[C]//Computer Vision and Pattern Recognition.IEEE,2016:770-778.
[21]He K,Zhang X,Ren S,et al.Identity mappings in deep residual networks[C]//European Conference on Computer Vision.Springer,Cham,2016:630-645.
[22]Yang Li,Chunxiao Fan,Yong Li,et al.Improving deep neural network with multiple parametric exponential linearunits[J].arXiv preprint arXiv:1606.00305,2016.

