基于人工蜂群算法的无人机协同路径规划
夏 瑞,赵 磊,吴书宇,李 军
(四川大学 电子信息学院,四川 成都 610200)
在当今世界,随着智能化自主化研究的不断深入,无人机作为航空领域的标志性成果之一,得到了更加广泛深入的研究,而关于无人机的可行性路径的规划更是一大研究热门,对路径规划的研究始于20世纪60年代,国内外学者提出了大量的路径规划算法,包括A*算法、Voronoi图算法引、动态规划方法、仿生学算法等[1]。
由于路径规划问题具有高时间复杂度,所以问题的求解时间会随着问题的规模呈指数型增长,尤其在复杂环境或者搜索空间比较大的情况下,上述所有算法的计算成本会急剧增加。由此,本文提出了一种新的基于人工蜂群算法(Artificial Bee Colony,ABC)的非确定性和双向搜索机制结合的规划算法,用于无人机路径规划。
人工蜂群算法由土耳其学者Karaboga[2]于2005年提出,是通过模拟蜜蜂群体寻找优良蜜源的行为方式解决实际工程优化问题的仿生智能计算方法,由于其在优化方面的高效性能,人工蜂群算法自提出以来得到了众多学者的极大关注,随着研究的不断深入,人工蜂群算法得到不断的改进,应用的领域也越来越广。
同时,本文综合考虑多无人机群的任务和任务区域的特点,合理构建了多UAV机群执行任务的问题模型,将以上提到的方法应用于多无人机群的路径规划问题的研究中,初步实现多无人机的协同规划的两种模型[3]。
1 无人机路径规划
1.1 环境模型及规划空间的建立
1.1.1 针对小型无人机的三维环境建模
对于小型无人机,其面对的飞行环境实际情况比较复杂,且无人机受到其机动能力的限制,因此,如何保证规划出的航路安全可飞是此类情况需首要解决问题。文献[4]提出了一种综合平滑算法,通过对地形坡度和曲率进行限制和平滑处理,使无人机在各个方向上的离地距离在安全范围内。采用这种综合地形平滑算法,可以得到综合等效地形曲面z(x, y),如图1所示,在此基础上,计算最小安全离地高度h[5],并与曲面z(x, y) 相叠加,可得到一个新的安全飞行曲面H(x, y )。该曲面可表述为:

本文将在所形成的安全飞行曲面上,通过人工蜂群算法对其进行限制搜索,即可在安全曲面上得到三维航路,保证了飞行的安全性。
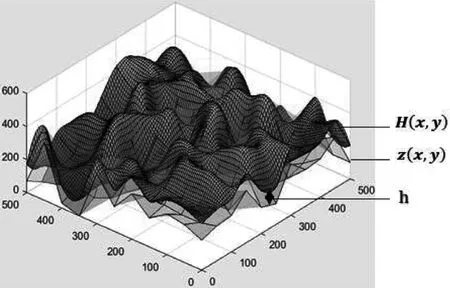
图1 综合等效地形
1.1.2 针对体型较大无人机的三维环境建模
对于较大型的无人机,其飞行航路虽然是三维的,但在实际情况中,可以考虑其是在定高飞行时的航路规划,在二维空间内搜索航路。文献[6]给出如下方法。
一般的地形可分为平原、山地以及高原等,为了模拟各类地形,可采取简化的方法来构建环境模型。以山地地形为例,单个山峰个地形可由如下公式模拟:

公式中,Z(x,y)表示山峰地形的高度,z为基准地形高度z0上山峰的高度;x0、y0是山峰中心O的坐标;在一定高度H上取山地截面,可得到一椭圆形。该椭圆形长轴长为a,短轴长为b,a,b值越大,则山峰越平坦,反之则越陡峭,如图2所示。

图2 山峰威胁示意
因此,可以将山峰威胁定高H二维平面时,威胁模型可表示为(x,y,max(a,b)),max(a,b)为取a,b中的最大者。该区域为无人机不可飞区域,无人机一旦进入该区域则会坠毁,即在该区域内无人机损坏概率为1。该区域用如下集合表述:

因此,将地形威胁信息表示为(x,y,max(a,b))。
我们选取截取后得到的椭圆形,以长轴为直径,O为圆心画圆,可得出地形的近似模拟。经过Matlab模拟可得如图3所示的环境模型。
图3 Matlab仿真地形示意
1.1.3 威胁区域的量化
有效地躲避防空威胁是无人机路径规划的主要目的之一。在对无人机进行航路规划之前,需要对威胁建模并转化为规划算法能够使用的量化信息。如果依据每种防空武器的特性精确建立各种威胁模型,分析起来极其复杂。本文采用简化模型的方法,如Menon等[7]提出了最小威胁曲面的概念,该方法主要根据威胁作用强度和作用半径将其等效为特殊山体,然后叠加到数字地图上的相应位置,得到综合威胁和地形地物的等效数字地图(见图4),从而将威胁回避转化为地形回避来处理。

图4 威胁区域与地形叠加示意
1.2 单无人机路径规划
1.2.1 单无人机路径规划问题描述
单无人机的路径规划需要模拟出外界地形环境条件参数和飞行过程中的可能威胁区域,综合考虑无人机自身的性能,如无人机的飞行高度、转角度数、飞行距离等,规划出一条从起点到终点的满足各方面要求的合理路线。
1.2.2 约束条件
实际无人机路径规划有很多约束条件,比如飞行途中的障碍物及可能发生危险的区域、无人机自身性能的限制,使得路径规划必须在这些约束下进行。通常考虑的约束条件有:最小飞行长度、最大飞行距离、飞行转弯夹角、威胁区域。
(1)最小飞行长度。
鉴于无人机在改变飞行状态之后持续直线飞行有着最小长度l min的限制,需约束最小飞行长度,即算法中路径规划任意两相邻节点之间的距离Li应满足:

(2)最大飞行距离。
由于考虑无人机能够携带的燃料有限,无人机的飞行总路径需要受到一定的限制,可分为以下两种情形。
①如果没有设定最大飞行距离,路径规划就以寻找到最短路径为目的,尽可能规划出可行的总长短的路径。
②设定了最大飞行距离Lmax,则对于路径总长度应该满足:

(3)飞行转弯夹角。
无人机在飞行转弯过程中有着对转弯角度的要求,如果转弯角度过小无人机则无法完成转弯动作,因此在对路径选择的时候需要规定转角范围。
如图5所示,设已完成的点N1,N2,接下来需要确定的路径节点N3,本路径采用余弦公式利用向量计算得到N1N2,N2N3两段路径的夹角的余弦值:
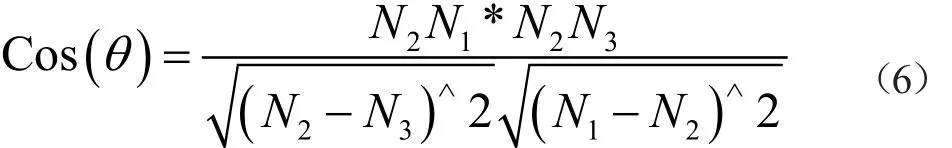

图5 飞行转弯夹角示意
若设定θ为钝角时满足无人机飞行转弯性能限制,则转换为满足条件:

(4)威胁区域。
威胁区域即无人机飞行途中遇见的如有导弹打击、雷雨等不便通过的区域,在实际情形中无人机可能有0~1的概率不可飞过威胁区域,为了使情况简单,本路径一律使用威胁区域的威胁因素为1,即不可进入威胁区域,处理原理与不完全概率一致。
对于一个以中心点为圆心,半径为R的威胁区域,无人机路径需要避开,要求路径节点在此区域之外,如图6所示,即满足:


图6 威胁区域
其中可能存在两节点不在威胁区域内,但是连接起来之后的路径有部分在威胁区域内,则可以使用增加节点数量的方法使路径全部置于威胁区域之外,如图7所示。

图7 威胁区域特例
本文采用ABC算法对路径规划问题进行求解,则需要建立合适的代价函数。为此,本文将所有约束条件通过公式(9)统一起来,产生一个总的代价函数。fk为各约束条件表达式,Weightk表示不同的约束条件所占权重大小,通过在仿真过程中不断改变权重比例关系能得到产生较好路径的最佳权重比。

求解最优解点就变成了求解该代价函数最小值是对应的各坐标参数。
1.2.3 航迹规划算法步骤
(1)初始化算法及其参数,主要设定的参数有起点setstartj、终点setfinalj、威胁区域相关信息(威胁坐标及威胁区域半径)、路径夹角与长度所占权重Weightk、算法迭代次数MaxCycle、算法运行次数2*runtime、蜜蜂总数NP、食物总数NP/2、环境上下限(xmax,xmin)、环境维度D、蜜源未更新次数上限NP*D(limit)、路径节点数node、初始化路径节点数组GlobalParamsmj={setstartj;0; setfinalj},j={1、2、3},为D维解向量的某个分量,m={1、2、3……node}。
其中,对于路径节点数的确定本文采用动态选取的方式,即对于不同长度的路径确定不同数量的节点数使节点大致呈均匀分布,通过对起点终点直接连线求得路径直线长度L,反复调试设定不同的两相邻节点之间长度Lfen,最终得出最合适的节点间距Lfen,且runtime=node+1。

(2)改进ABC算法中初始蜜源(节点)的产生方式,在原有公式(11)的基础上,再通过公式(12)、(13)增加维度限制条件,简化搜索范围,同时使所产生的节点均匀化分布。

式中:i={1、2、3……NP/2},为蜜源(可行解)编号。

iter为与MaxCycle做比较的计数器。
(3)根据代价函数函数计算公式(9)计算每个可行解的总代价值,再通过公式(14)计算其适宜度。
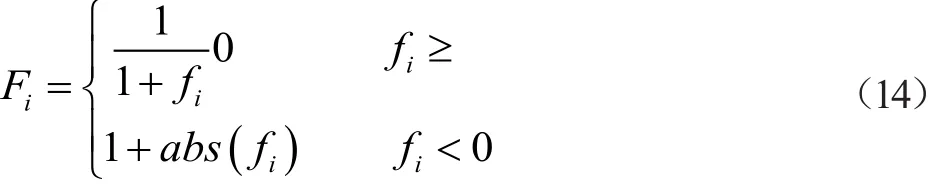
(4)根据公式(15)进行开采,寻找新节点。

其中:xk代表领域蜜源,k取值于{1,2,…NP/2},且k不等于1,φij是取值在[-1,1]内的随机数,通过式(15)得到新蜜源后,利用贪婪算法,比较新旧蜜源适应度,选择优者。
(5)跟随蜂通过公式(16),用轮盘赌方式进行贪婪选择蜜源,通过公式(15)进行进一步开采。

蜜源拥有参数trial,当蜜源更新被保留时,trail为0,反之,trail加1。从而trial能统计出一个蜜源没有被更新的次数,用于limit的比较。
(6)如果一个蜜源经过多次开采没被更新,也就是trial值过高,超过了预定阈值limit,那么需抛弃这个蜜源,启动探索峰阶段。这体现了ABC里自组织的负反馈和波动属性[8]。在该阶段里,探索蜂利用步骤(2)中的公式随机寻找新的蜜源来代替被抛弃蜜源。
(7)迭代次数iter加一,重复(3)~(6)过程,得到更优适应度的节点,直至迭代次数达到MaxCycle,运行次数r+1。
(8)继续执行第(3)~(7)步,求解下一个节点,直至规划完node个节点。
(9)路径节点优化,增加步骤(2)中的维度限制条件

(10)对产生的节点进行B样条平滑处理,绘制规划效果,输出相应规划结果。
1.2.4 算法规划特点
(1)采取智能算法解决无人机路径规划问题。
将人工蜂群算法结合无人机路径规划这一特定问题,对算法进行相应改造,以适用于这一特定问题的解。基于ABC算法的路径规划问题对应关系如表1所示。
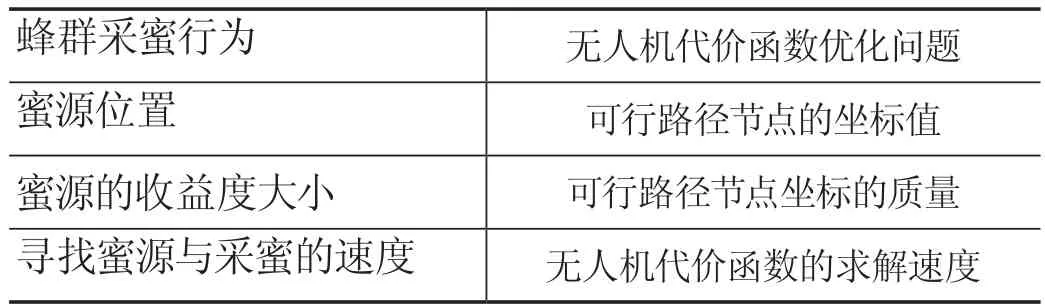
表1 基于ABC算法的路径规划问题对应关系
(2)采用非确定性规划方法。
由于确定性规划方法存在一定的缺陷,我们采用随机搜索方法搜索航路。所谓确定性规划,即任意两个点之间的可选路径条数是可数的,而在非确定性规划中是无穷多的,与之特点对应的,其规划出来的路径具有更高的精确性。确定性规划方法和非确定性规划方法示意如图8—9所示。

图8 确定性规划方法示意
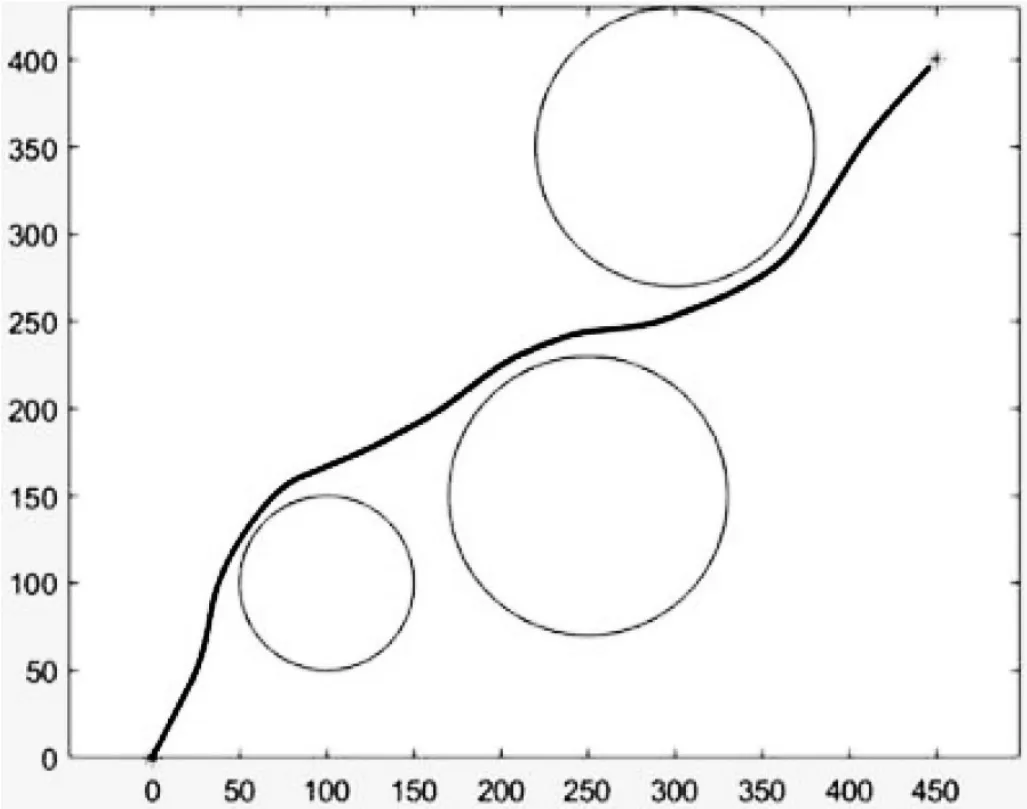
图9 非确定性规划方法示意
在随机方法中我们将路径规划这一大问题分解为路径中重要节点的规划问题上,采用此方法有以下优点:①可以通过调整航路节点的数目达到任意的精度。②将原始的规划问题分解为一组统一的规模较小的子问题。在每个子问题中,关心的仅仅是一个点的坐标。考察航路是否可行,是否满足约束条件变为仅考察一个点或者一条线段是否满足要求。③由于将航路规划问题局限为一系列航路节点,从而便于实现大量的并行/分布式计算,这与人工蜂群算法的特点很好融合。
(3)采用基于双向规划机制[1]的节点确定方法进行路径规划算法设计。
在传统路径规划算法中,一条路径的生成通常是从起点开始,到终点结束,不能充分发挥蜂群群体协作的特性,因此影响了算法的效率和收敛速度,而且不能很好满足任务的环境约束,基于双向搜索机制的路径节点确定方法能够有效解决这个问题。流程如图10所示。

图10 双向规划节点确定流程
方法具体步骤如下。
Step1:以起点开始,规划奇数位置的节点。根据起始两点距离,大致均匀化固定节点的横坐标值,使规划问题降维,即将这一个点的规划空间固定到以横坐标为定值的一平面(三维环境下)或一直线(二维环境下),将蜂群寻优过程进行间隔分块,进行双向路径节点规划,即按照(1,node,3,node-2···(node+1)/2)的顺序规划,寻找到满足使代价函数值最小的点。其中node为路径节点个数,且为奇数。
Step2:利用Step1中所产生节点,同样采用降维思想,固定偶数位置节点的纵坐标值。按照(2,4,6,···node-1)的顺序规划,寻找到满足使代价函数值最小的点。
Step3:采用同样的方法,固定奇数位置节点的横坐标值,再次对奇数位置的节点进行规划。
Step4:采用同样的方法,固定偶数位置节点的纵坐标值,再次对偶数位置的节点进行规划。
根据理论分析,此方法的Step2~Step4可以一直循环进行,每循环一次,效果便会好一些,但是时间代价会成倍增加。
1.2.5 B样条路径平滑算法
B样条(De Boor)[9]在数学的子学科数值分析里是样条曲线一种特殊的表示形式,由Isaac Jacob Schoenberg创造的,是基(basis)样条的缩略。B样条方法具有表示与设计自由型曲线曲面的强大功能,是形状数学描述的主流方法之一,另外B样条方法是目前工业产品几何定义国际标准—有理B样条方法(NURBS)的基础。B样条方法兼备了Bezier方法的一切优点,包括几何不变性、仿射不变性等,同时克服了Bezier方法中由于整体表示带来不具有局部性质的缺点(移动一个控制顶点将会影响整个曲线)。B样条曲线方程可写为:

其中:di(i=0,1...n)为控制顶点(坐标),Ni,k(i=0,1...n)为k次规范B样条基函数,最高次数是k。基函数是由一个称为节点矢量的非递减参数u的序列U:u0≤u1≤...≤un+k+1所决定的k次分段。
B样条的基函数通常采用Cox-deBoor递推公式:

式中:i为节点序号,k是基函数的次数,共有n+1个控制顶点。注意区分节点和控制顶点,节点是在节点矢量U中取得,控制顶点则是坐标点,决定B样条的控制多边形。CoxdeBoor递推公式是B样条曲线的定义的核心,该部分在程序中实现可采用递归的方式。
常见的B样条曲线有以下3种。
①均匀B样条曲线:节点矢量中节点为沿参数轴均匀或等距分布,如图11所示。
②准均匀B样条曲线:其节点矢量中两端节点具有重复度k+1,即u0=u1=...=uk,un+1=un+2=...=un+k+1,所有的内节点均匀分布,具有重复度1,如图12所示。
③分段Bezier曲线:其节点矢量中两端节点的重复度与类型2相同,为k+1。不同的是内节点重复度为k。该类型有限制条件,控制顶点数减1必须等于次数的正整数倍,即n/k=正整数,如图13所示。

图11 均匀B样条曲线
图12 准均匀B样条曲线

图13 分段Bezier曲线
本文利用人工蜂群算法得出路径散点之后,采用准均匀B样条路径平滑方法平滑散点,路径规划效果有了显著的改变(见图14—15)。产生交集。多无人机规划路径产生示意如图16所示。

图14 平滑之前
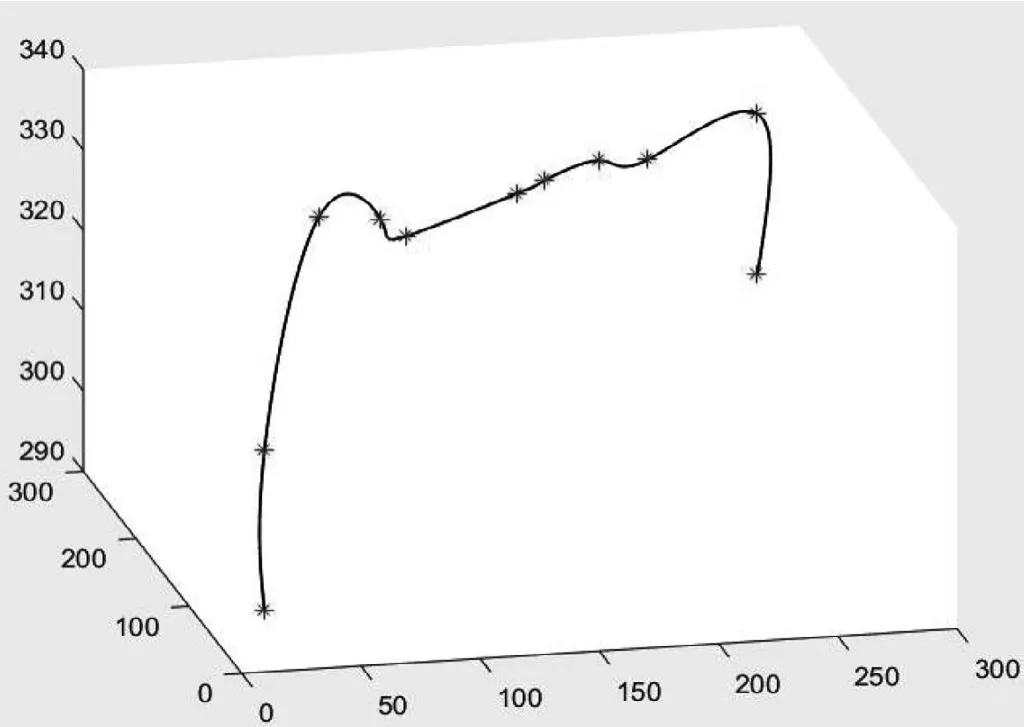
图15 平滑之后
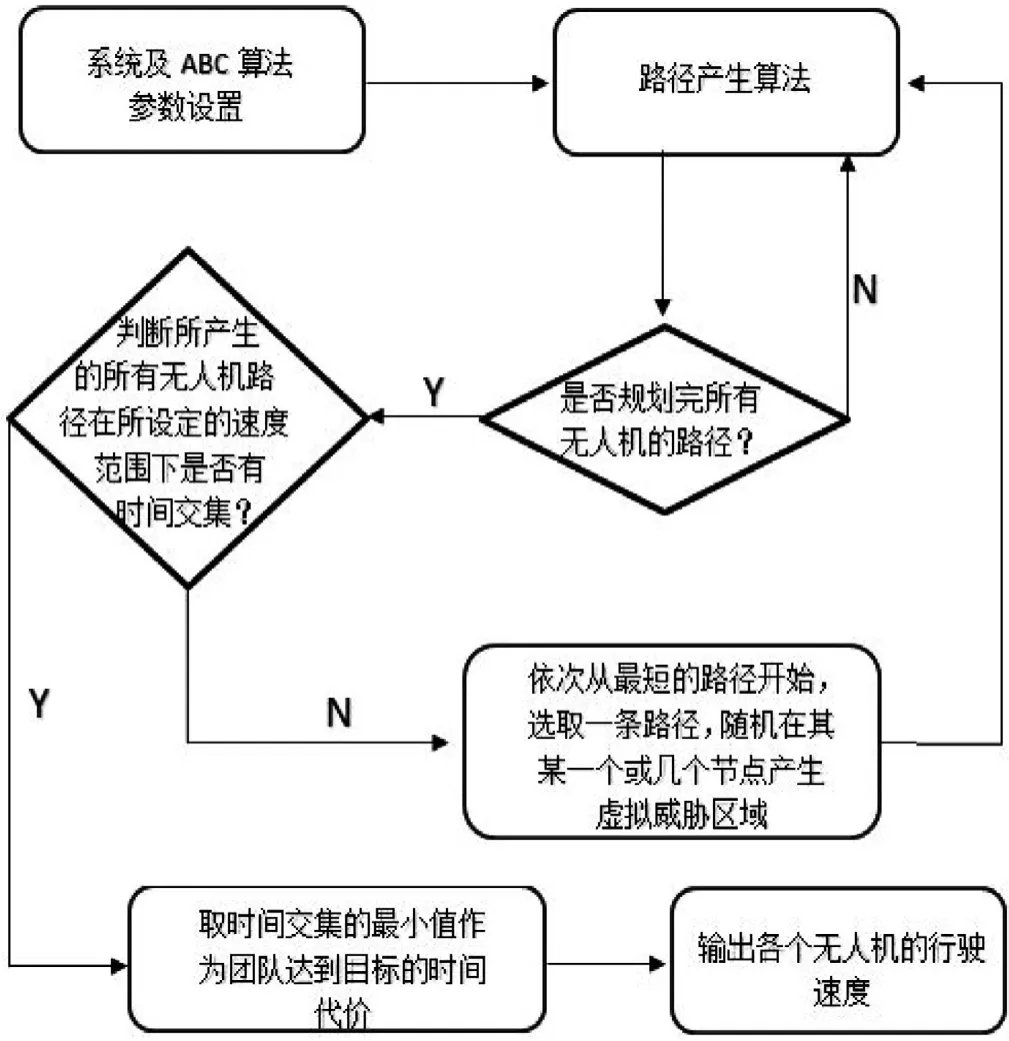
图16 多无人机规划路径产生示意
1.3 多无人机路径规划
本文应用前面所提到的规划算法,初步建立了两个多无人机协同规划的模型,并通过Matlab对其进行仿真实现。
(1)考虑多无人机不同起点,同一终点,同时起飞,同时到达。规划时,系统根据文章前面提到的路径产生算法,生成所有无人机路径,并判断所有无人机在所设定的速度范围下是否有时间交集,若有,则取时间交集的最小值作为团队达到目标的时间代价,并输出各个无人机的飞行速度。若没有,则依次对路径最短的无人机根据公式(8)产生一个虚拟的威胁区域进行重新规划,直到所有无人机的飞行时间
(2)考虑多无人机不同起点,同一终点,同时起飞,按照指定顺序和时间间隔依次到达。规划时,系统给每架无人机分别规划路径,计算所指定的第一架无人机以最大速度飞行的时间,对此后的无人机依次按照上一架无人机的飞行时间延时指定的时间间隔,然后依次对目前所规划的时间进行越界判断(即能否在此时间下通过自己的路径),若能,则根据每架无人机的规划时间计算出各自飞行速度,否则比较计数器和无人机的数量,若计数器小于无人机数,则以越界无人机通过其路径的最快速度为基准,对其前后的无人机,依次按照上一架无人机的飞行时间延时指定的时间间隔,然后计数器加一,重复之前的判断操作。若计数器数大于无人机数,则输出错误,没有规划方案。特别的,当间隔时间为0的时候,可实现同时到达。多无人机规划示意如图17所示。

图17 多无人机规划示意
其中M为计数器,初始值为0。
2 仿真结果
采用上述航路规划方法,利用Matlab R2016a对所设计的算法进行仿真。环境模型为威胁区域与障碍物的叠加,得到的航路均为经均匀化B样条路径法平滑后的航路。
2.1 单无人机规划
(1)实验1:在一块500×500的数字地图上进行仿真,仿真基本参数如下:无人机最小步长为30,飞行器的起点和目标点坐标分别为(0, 0),(450, 400),两点直线距离为602.0797,最大航程约束为直线距离的1. 5倍。仿真实验1所得结果如图18所示。
得到路径的长度为653.0710,规划时间4.666 s。

图18 仿真实验1所得结果
(2)实验2:在一块500×500×500的数字地图上进行仿真,仿真基本参数如下:无人机最小步长为30,飞行器的起点和目标点坐标分别为(15.15, 30.3, 295.9),(449.5, 459.6,422),两点直线距离为623.5861,最大航程约束为直线距离的1.5倍。仿真实验2所得结果如图19所示。

图19 仿真实验2所得结果
得到路径的长度为661.6694,规划时间22.240 s。
2.2 多无人机规划
(1)实验3:在一块500×500的数字地图上进行仿真,仿真基本参数如下:无人机最小步长为30,V∈(3,30),飞行器的起点坐标分别为(0, 20),(50, 450),(500, 50),(600, 600),编号依次为1、2、3、4。设置无人机到达顺序为{1,3,4,2},时间间隔为5 s。仿真实验3所得结果如图20所示。多无人机规划结果如表2所示。
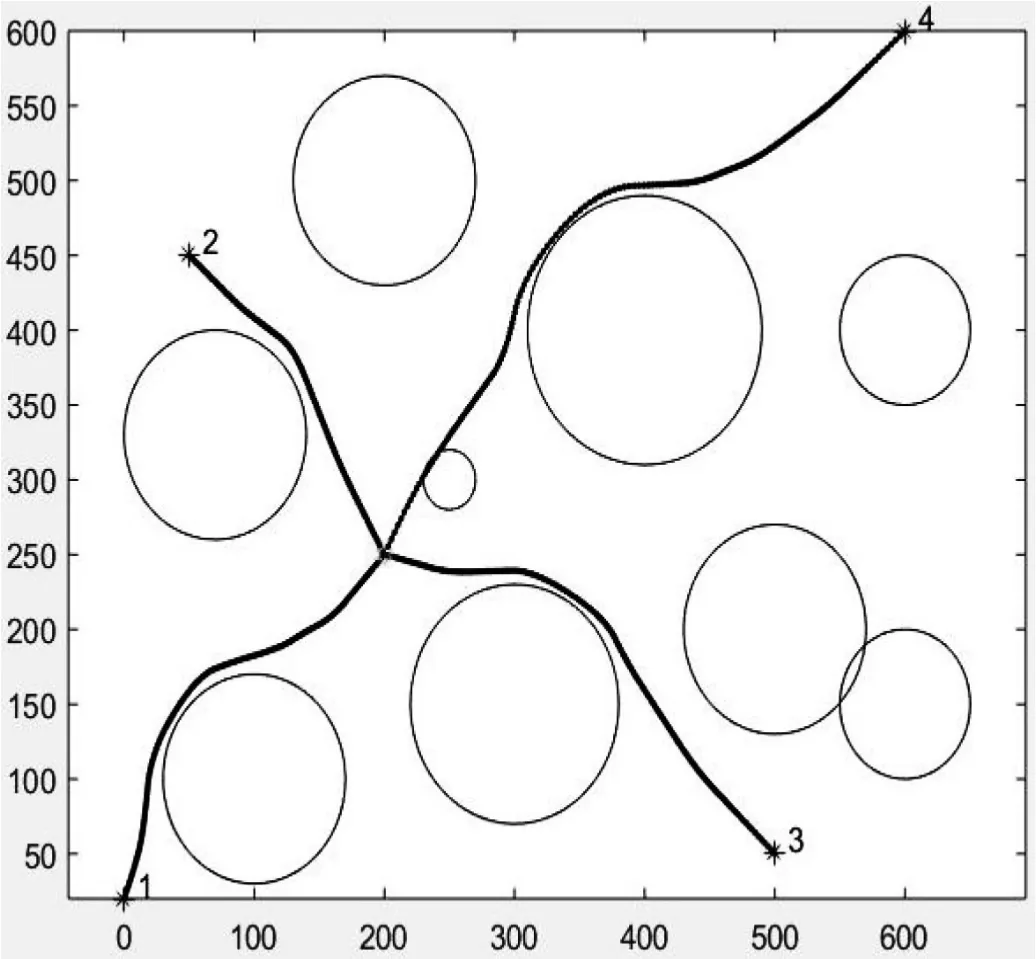
图20 仿真实验3所得结果

表2 实验3多无人机规划结果
所示结果符合预期,规划时间为6.962 s。
(2)实验4:在一块500×500×500的数字地图上进行仿真,仿真基本参数如下:无人机最小步长为30,V∈(3,30),飞行器的起点坐标分别为(176.8, 237.4,254.5),(161.6, 363.6, 429),(454.5, 146.5, 228.2),(393.9,308.1, 234.3),编号依次为1、2、3、4。设置无人机到达顺序为{1,4,2,3},时间间隔为9 s。多无人机规划结果如表3所示。
所示结果符合预期,规划时间为32.912 s。
仿真结果表明,采用双向规划机制的非确定性节点规划能很好地融入ABC算法,并能在较短时间内得到较好的路径。

表3 实验4多无人机规划结果
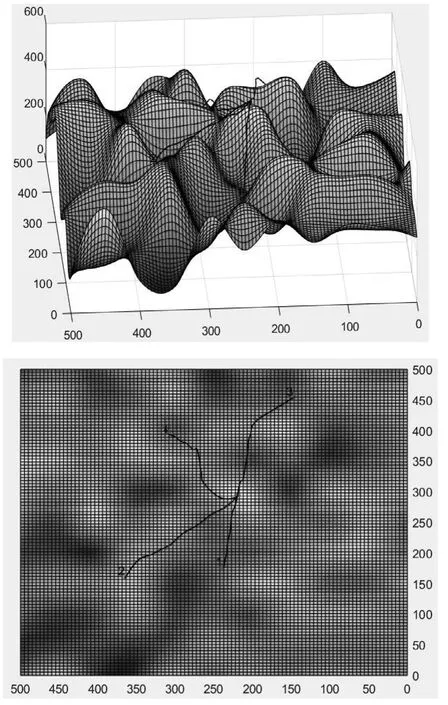
图21 仿真实验4所得结果
3 结语
本文给出了一种基于改进人工蜂群算法的航路规划方法实现。该方法将规划空间的预处理和人工蜂群算法相结合,通过建立地形安全曲面和量化威胁信息,简化规划空间。在传统人工蜂群算法的基础上,改进了算法中食物产生的方式,将航迹规划分解为各节点的规划,并引入双向规划机制,大大提高了产生航迹的质量。同时应用我们给出的路径规划算法,对多无人机的两种协同模型做出初步实现,仿真结果表明,算法可以快速规划出满足约束条件的三维航路,并能有效实现多无人机的初步协同,具有较强的工程可实现性。
[1]李喜刚,蔡远利.基于改进蚁群算法的无人机路径规划[J].飞行力学,2017(1):52-56.
[2]KARABOGA D.An idea based on honey bee swarm for numerical optimization[D].Erciyes:Erciyes University,2005.
[3]江铭炎,袁东方.人工蜂群算法及其应用[M].北京:科学出版社,2014.
[4]胡志忠,徐克虎,沈春林.低空突防用数字地形的平滑处理[J].南京航空航天大学学报,2000(5):493-498.
[5]吴强,曹义华,金长江.最小飞行高度的计算[J].战术导弹技术,2003(2):21-24.
[6]严建林.基于进化算法无人机航路规划技术研究[D].南京:南京航空航天大学,2008.
[7]MENONPKA,KIME,CHENGVHL.Optimal trajectory synthesis for terrain-following flight[J].Journal of Guidance Control and Dynamics,2012(4):807-813.
[8]BONABEAU E,DORIGO M,THERAULAZ G.Swarm intelligence: from natural to Artificial systems[M].Oxford:Oxford University Press,1999.
[9]施法中.计算机辅助几何设计与非均匀有理B样条(修订版)[M].北京:高等教育出版社,2013.

