翻转在解中考题中的应用
张桂芳
【摘 要】几年来我省的中考数学试题,多数取材于教科书,是在教科书中的例题、练习题、习题的基础上延伸或扩展而成的。教学中应以教科书为蓝本,加强对容易题的训练,掌握学习方法,对例、习题能举一反三,触类旁通,变条件、变结论、变图形、变式子、变表达方式等,引导学生构建起初中数学的基础知识网络。
【关键词】翻转;中考;初中数学;解题
近几年来,绍兴市中考数学命题在前几年积淀的基础上又有新的创新,试题遵循《数学课程标准》中有关评价的基本理念,试卷的编制重视对学生能否结合具体情境发现并提出数学问题、能否从图形全等变换角度分析并选择恰当的方法解决问题、能否运用规律解决问题或对未来事件作出合理预测与判断的考察。这一理念在下题中得到充分体现。
一、自主探究,事半功倍
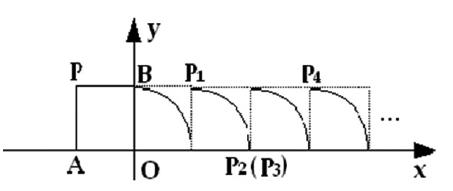
题目:如图,将边长为1的正方形OAPB沿x轴正方向连续翻转2006次,点P依次落在点P,P1,P2,P3,P4……,P2006的位置,则P2006的横坐标x2006= 。
分析:本题可先在平面直角坐标系中找出P1,P2,P3,P4点的横坐标,然后再继续寻找P5,P6,P7,P8点的坐标……实际上是4次翻转1个周期,P点的横坐标依次移动4,从而点P2006的横坐标就自然而明了。
解答:当点P第一次翻转落在点 P1,此时点P水平方向运动了2个单位长度到达点P1的位置;第二次翻转落在点 P2,此时点P1水平方向运动了1个单位长度到达点P2的位置;第三次翻转点P2不动,即点P2与点P3重合,第四次翻转落在点P4,此时点P3水平方向运动了1个单位长度到达点P4的位置;第五次翻转时与点P的运动规律一模一样;即从第一次开始依次翻转4次为一个周期,点P水平方向共运动了4个单位长度;在翻转第2006次时,共运动了501个周期,再加2次,即(2006÷4=501……2),因为运动501个周期点P水平方向运动了501×4个单位长度, 第2005次翻转时,点P2004水平方向运动了2个单位长度到达点P2005的位置;第2006次翻转时,点P2005水平方向运动了1个单位长度到达点P2006的位置,共运动了501×4+2+1=2007个单位长度,在原正方形中,点P开始运动时横坐标为-1,所以点P2006的横坐标x2006=2007-1=2006。
二、功能分析,举一反三
(一)注重操作,形成思路
数学学习方法有很多种,而这题重点突出以下两种學习方法:
第一种是特殊化方法。当人们在解决一个复杂问题很难入手时,可以先解决这个复杂问题中的一部分问题:当点P第一次翻转落在点 P1,此时点P水平方向运动了2个单位长度到达点P1的位置;第二次翻转落在点 P2,此时点P1水平方向运动了1个单位长度到达点P2的位置;第三次翻转点P2不动,即点P2与点P3重合,第四次翻转落在点P4,此时点P3水平方向运动了1个单位长度到达点P4的位置;这一部分问题就是这个复杂问题的特殊化,人们可以把解决这个特殊问题获得的方法加以推广,最终解决复杂问题。
第二种是类比与联想。引导学生从特殊的现象:从第一次开始依次翻转4次为一个周期中发现、归纳、总结形成规律,运用规律解决问题或对未来事件作出合理预测与判断:在翻转第2006次时,共运动了501个周期,再加2次。鼓励学生能对问题进行类比、联想、反思,能合理的评判自己的思维过程,总结、提炼已有经验,形成规律。
(二)注重创新,形成策略
我们在研究一个数学问题时,常常要借助已有的数学知识和相应的数学活动经验对这个问题进行各种各样的猜测。正如牛顿说的“没有大胆的猜想,就没有伟大的创新”那样,这些猜测可能是正确的,也可能是错误的。为了进一步探索与验证,必须要做相关的数学实验和数学活动。运动变化和开放性试题是近几年试卷中一道亮丽的风景线,本题立足于常见的基本图形,把传统的综合题改造成一个要求学生发现猜想的填空题。本题通过动手操作,将边长为1的正方形OAPB沿x轴正方向连续翻转1、2、3、4、5、6、7、8…次,这样手脑并用获得直接的感性认识:(1)第五次翻转时,点P与第一次翻转的运动规律一模一样;(2)按真实实验方式展开思维活动:在翻转第2006次时,共运动了501个周期,再加2次,即(2006÷4=501……2),因为运动501个周期点P水平方向运动了501×4个单位长度, 第2005次翻转时,点P2004水平方向运动了2个单位长度到达点P2005的位置;第2006次翻转时,点P2005水平方向运动了1个单位长度到达点P2006的位置,共运动了501×4+2+1=2007个单位长度,为抽象的数学思维提供了直观模型,就能有效地解决问题。
(三)注重选拔,形成梯度
一般地说,水平考试主要是为了区分被试者是否达到应达到的合格水平,因此测试目标比较基本、一般难度不大;而选拔性测试主要是为选拔,从被试者中挑选出符合预定目标的人才,因此测试除了基本目标外,还有一定比例的综合目标。而我们的中考虽是检测初中学生三年的学习情况,同时也具有甄别选拔功能,所以其结果要有个较高的区分度。因而对于这样的探索题设置能让学生充分发挥其能力,使不同水平的学生得到相应的分数,让学生的成绩拉开档次,形成梯度。
本题情景设计新颖,呈现方式富有新意,体现了数学与生活的联系,在考查中引导学生经历解决实际问题的过程,体验运用数学知识解决实际问题的情感。考查学生从图形全等变换的角度思考问题的能力,考查基本的数学建模能力,考查学生的抽象思维能力和创新意识。
几年来我省的中考数学试题,多数取材于教科书,是在教科书中的例题、练习题、习题的基础上延伸或扩展而成的。教学中应以教科书为蓝本,加强对容易题的训练,掌握学习方法,对例、习题能举一反三,触类旁通,变条件、变结论、变图形、变式子、变表达方式等,引导学生构建起初中数学的基础知识网络,删除某些复习资料中的偏题、难题和怪题,全面抓基础落实。

