圆盘区域下系统不确定项容忍区间分析

张 瑶，王福忠，姚 波

(1.沈阳师范大学 数学与系统科学学院，辽宁 沈阳 110034； 2.沈阳工程学院 基础教学部，辽宁 沈阳 110136)

线性系统的极点配置问题早已经成为控制界的热门问题。文献[1-2]给出了状态反馈下的圆盘区域极点配置的充要条件。文献[3]提出了动态输出反馈的圆盘区域极点配置问题，但是在实际的系统中，状态反馈对系统状态的提取很难做到。动态输出反馈又过于复杂，消耗能量过大。因此，引入了静态输出反馈。文献[5-12]是对执行器增益偏差容忍区间及一些性能指标容忍区间的分析。然而，系统的不确定性是客观存在的。参数的不确定性，可能会导致系统失去某些性能，甚至是稳定性。为了使系统依然能够保持某些较好的性能且避免保守性带来的能量损耗，对系统参数不确定范围型性的分析就尤为重要。由于状态反馈具有局限性，所以静态输出反馈不确定参数容忍区间的分析是具有实际研究价值的。

将圆盘区域极点配置与静态输出反馈结合，考虑系统参数的波动，分析参数的变化对系统性能的影响，给出了系统不确定参数容忍区间的概念。通过分析每个不确定参数波动对系统性能的影响程度，进而得到了容忍区间的算法。比较各个参数的容忍区间，判断出每个不确定性对系统的影响水平。容忍区间越小，对系统的影响越大；相反则次之。最后，通过仿真实例对结论加以验证。

1 问题描述

考虑如下线性系统：

(1)

式中，x(t)为n维状态；u(t)为p维输入；y(t)为q维输出；系数矩阵A,B,C是给定的相应维数常矩阵。

对于线性系统(1)，设计静态输出反馈控制器：

u(t)=Ky(t)

(2)

由系统(1)和静态输出反馈控制器(2)，构成如下闭环系统：

(3)

式中，K为需要设计的矩阵。

引理1[13]：矩阵A的所有特征值均在半径为r，中心在(-q,0)的圆盘中，当且仅当存在对称矩阵X，使得

(4)

引理2[14]：已知M是n×n的对称正定矩阵(m≤n),N是适维的行满秩矩阵，那么矩阵NMN′可逆。

证明：设NMN′X=0∴X′NMN′X=0

整理得(N′X)′M(N′X)=0∵M是n×n正定对称矩阵∴N′X=0∴NN′X=0

又∵NN′是可逆的，所以只有X=0这个零解。

综上所述，方程只有零解，即NMN′是可逆的，引理得以证明。

引理3[4]：若XY=Z，其中Y、Z为m×n维的行满秩矩阵 ，则X可逆。

2 主要结果

定理1：系统(1)存在静态输出反馈控制器K，且该闭环系统的极点能够配置到半径为r，中心为(-q,0)的圆盘中，当且仅当存在正定的矩阵X和矩阵U，使得：

(5)

如果LMI的可行解为(U,X)，则u(t)=UV-1x(t)为系统(1)的一个静态输出反馈控制器(2)，其中V由VC=CX所求。

证明：由引理1可知，闭环系统(1)的极点配置到半径为r，中心在(-q,0)的圆盘中的充要条件是：存在正定对称矩阵X，使得

(6)

将VC=CX，U=KV代入(6)中有

下证V可逆：

对等式VC=CX两边乘以CT得

VCCT=CXCT

则V=CXCT(CCT)-1

因为CXCT是可逆的，所以V可逆。即定理得证。

如果考虑系统的不确定参数，由此闭环系统为

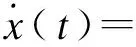
(7)

若系统(7)中第ij项出现波动，那么系统的单一不确定因素增益偏差模型是

dimax-r=0

3 仿真实例

考虑如下系统：

系统的极点，配置到半径为r=2，中心为(-2,0)的圆盘中的静态输出反馈控制器为K=-0.4178，如图1所示。

图1 圆形极点配置极点分布

图1表述的是将不稳定的线性系统极点配置到半径为r=2，中心为(-2,0)的圆盘中，且使系统保持渐近稳定。现对此系统加入不确定参数，考虑系统中的不确定因素对圆盘区域极点分布的影响，如图2所示。

图2 极点脱离圆盘

图2表述的是考虑相同的系统加入不确定参数后极点脱离圆盘。

图3 不确定项t11引起的圆盘极点的变化

图3描述的是系统不确定参数t11∈[-5，5]时，系统不确定参数容忍区间的分析，可以看出不确定参数t11在波动时，其增益偏差的容忍区间为(-3.9,0.2)；图4描述的是系统不确定参数t22∈[-5，5]时，系统不确定参数容忍区间的分析，可以看出不确定参数t22在波动时，其增益偏差的容忍区间为(-4.1,0.5)。

通过上述数据的分析可知，不确定参数t11对系统性能的影响比不确定参数t22对系统性能的影响大。

图4 不确定项t22引起的圆盘极点的变化

4 结 论

在现实的工程实例中，系统中的很多不确定因素是不可避免的，设计者若能很好的掌握每个不确定参数对系统的影响程度，那么在设计过程中可以减少能源上的浪费，同时也能保证系统有较高的安全性能。

通过将圆盘区域极点配置与静态输出反馈结合，避免了状态反馈和动态输出反馈给系统带来的不足。在此基础上，考虑了系统不确定参数变化，观察到不确定参数波动后极点会脱离圆盘，为了保证系统的稳定并且降低一定的保守性，研究了系统不确定参数容忍区间的概念及其算法，得到了不确定参数变化对系统的影响程度：容忍区间越小，对系统性能的影响越大；容忍区间越大，对系统性能的影响相应越小。系统设计者可以比较系统各个不确定参数的容忍区间，进而在系统的设计过程中降低能源的浪费，保证系统有较好的性能。

[1] 滕青芳,范多旺.不确定系统的鲁棒状态反馈区域极点配置[J].计算技术与自动化,2006,25(1):8-10.

[2] 姚 波,张庆灵,王福忠,等.具有传感器故障的可靠圆盘极点配置[J].控制与决策,2004,19(3):346-348.

[3] 俞 立,陈国定,杨马英.不确定系统的鲁棒输出反馈区域极点配置[J].控制理论与应用,2002,19(2):244-246.

[4] 葛 迪,姚 波,王福忠.不确定系统静态输出反馈可靠控制[J].计算技术与自动化,2016，35(1):5-8.

[5] ZHANG Bao-lin,HAN Qing-long,ZHANG Xian-ming.Event-triggered H∞reliable control for offshore structures in network environments[J].Journal of Sound and Vibration,2016,368:1-21.

[6] WANG Jun-wei，WU Huai-ning，LI Han-xiong.Static output feedback control design for linear MIMO systems with actuator dynamics governed by diffusion PDEs[J].International Journal of Control,2014,87(1):90-100.

[7] 刘子平,王福忠.具有圆盘极点约束的H∞性能指标容忍区间分析[J].数字技术与应用,2011,(11):171-172.

[8] 王福忠,辛 健.基于极点配置执行器增益偏差容忍区间的分析[J].控制工程,2012,19(5):740-742.

[9] 于 洁,王福忠,姚 波,等.梯形区域下执行器增益偏差容忍区间的分析[J].沈阳工程学院学报：自然科学版,2015,11(2):171-175.

[10]姚 波,陈媛媛,王福忠.基于圆盘极点约束的系统不确定项容忍区间分析[J].平顶山学院学报,2015,30(2):5-8.

[11]王晓萌,姚 波,陈媛媛.基于圆盘极点约束的系统不确定项容忍区间分析[J].井冈山大学学报：自然科学版,2016,37(3):1-3.

[12]武淑平，刘玉忠.时变时滞切换系统的指数稳定性及L2增益分析[J].沈阳师范大学学报：自然科学版,2016,34(3):282-286.

[13]徐艺超,王福忠,姚 波.条形区域极点配置静态输出反馈可靠控制[J].沈阳工程学院学报：自然科学版,2016,12(2):187-192.

[14]徐艺超,姚 波,王福忠.梯形区域极点配置静态输出反馈可靠控制[J].井冈山大学学报：自然科学版,2016,37(5):11-17.