Ku频段发夹型滤波器小型化设计

王 新，杨 凯，李其强

(中国电子科技集团公司第五十四研究所，河北 石家庄 050081)

0 引言

滤波器在微波毫米波系统中起着重要的作用，它可以用来分离和组合不同频率的信号。随着无线通信技术的快速发展亟需小型化的、性能优异的滤波器来减小系统的成本、提升系统的性能。微带线滤波器由于其结构紧凑、易于制造等特点受到了学者们的广泛关注[1-3]。

阶梯阻抗谐振器(Stepped-Impedance Resonators,SIR)通过改变阻抗比，不仅可以减小谐振器尺寸，还可以调整寄生通带的位置从而改善阻带特性[4-5]，文献[6]对四分之一波长、二分之一波长和一个波长的阶梯阻抗谐振器的原理及实际应用进行了详细的分析，包括其谐振条件、谐振器长度、寄生通带和等效电路。为了减小滤波器尺寸，文献[7]将二分之一波长阶梯阻抗谐振器应用于发夹型带通滤波器，在一定程度上减小了谐振器尺寸；Sagawa等人[8]提出了采用终端开路的平行耦合线取代开口环形谐振器[9-10]中的集总电容的小型化发夹型谐振器，进一步减小了谐振器的尺寸；Sheng-Yuan Lee等人[11]则通过将传统的发夹型阶梯阻抗谐振器与小型化的发夹型谐振器有机地结合在一起，进行合理的电路布局，设计出了极为紧凑的发夹型带通滤波器。

1 小型化谐振器

图1(a)为四分之一波长阶梯阻抗谐振器示意图，其由两段特征阻抗为Z1、Z2的传输线组成，电长度分别为θ1、θ2。忽略传输线的不连续性，开路端的输入导纳可以表示为：

(1)

式中，Y1=1/Z1，Y2=1/Z2。根据谐振器的谐振条件Yi=0，可以得到：

tanθ1•tanθ2=RZ，

(2)

式中，RZ=Y1/Y2=Z2/Z1。此时谐振器的总长度可以表示为：

(3)

由上式可知，当RZ小于1时，可以使谐振器小型化[4]。图1(b)为二分之一波长阶梯阻抗谐振器示意图，其基膜工作时中间对称点等效为地，分析方法与图1(a)一致。图1(c)为二分之一波长发夹式阶梯阻抗谐振器示意图，其由图1(b)演进而来。图1(d)为小型化的发夹式阶梯阻抗谐振器示意图，终端两段传输线之间存在耦合，文献[11]对该类型谐振器进行了详细分析，式(2)变为：

(4)

式中，Zoo为耦合线奇模阻抗。式(5)本质上与式(2)一致，对于图1(b)与(c)中的谐振器，终端两段传输线耦合很小，此时Zoo=Z2。

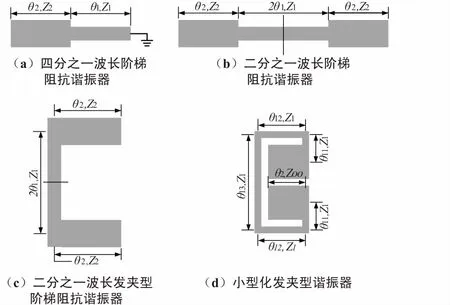
图1 阶梯阻抗谐振器原理示意

图2为发夹型小型化带通滤波器的结构示意图。采用阶梯阻抗谐振器使谐振器小型化，以此减小滤波器的尺寸。滤波器采用Al2O3陶瓷基板[12]，介电常数为9.9，损耗角正切为0.000 2，基板厚度0.254 mm。基板底层为滤波器地，顶层为不同阻抗的薄膜微带线。滤波器采用抽头方式与外界相连，抽头微带线特征阻抗为50 Ω。滤波器详细结构参数为：Wt=0.25 mm，W1=0.155 mm，W2=0.344 mm，W3=0.503 5 mm，L1=1.81 mm，L2=1.235 mm，S12=0.197 mm，S23=0.078 mm，S14=0.112 mm，S=0.081 mm，S1=0.125 mm，t=0.334 mm。

图2 滤波器结构示意图

2 滤波器设计

取传输线特征阻抗Z1=60.5 Ω，Z2=41.5 Ω，Zoo=25 Ω，带通滤波器的中心频率为11.85 GHz，根据式(1)～(4)可以初步计算出谐振器的尺寸，然后在仿真软件中进行微调，使得谐振器的谐振频率在滤波器中心频率附近。

当谐振器的尺寸确定后，谐振器之间耦合系数与谐振器之间距离的关系、谐振器外部品质因数与抽头位置的关系可以由文献[13]中的方法通过仿真软件萃取得到。图3为萃取得到的谐振器之间耦合系数(M)与谐振器之间距离(S)的关系曲线，由图2的滤波器结构示意图可知，在设计的滤波器中主要有三种耦合结构，其耦合系数分别为M12、M23和M14，其中M12为混合耦合，M23为电感耦合，M14为电容耦合。由图中可以看出，随着谐振器之间距离变大，谐振器之间耦合系数逐渐减小。图4为萃取得到的谐振器外部品质因数(Qe)与抽头位置(t)的关系曲线。

滤波器中心频率11.85 GHz，相对带宽(FBW)15%，传输零点位于10 GHz和13.7 GHz。根据滤波器指标可以得到四级切比雪夫带通滤波器的耦合系数矩阵与外部品质因数[14-15]为：

由图3与图4可以得到S12初值为0.2 mm，S23初值为0.075 mm，S14初值为0.195 mm，t初值为0.65 mm。由图2中的版图布局可以看出，谐振器I与谐振器IV之间耦合位置对谐振器II与谐振器III影响较大，因此S14实际值会比初值小，需在全波仿真中进行微调。

图3 耦合系数随谐振器间距变化曲线

图4 外部品质因数随抽头位置变化曲线

滤波器输入输出耦合采用抽头结构。二分之一波长谐振器，在谐振器中心两侧存在两个对称的馈电点，图5为两种不同馈电结构示意图，为了简化分析过程，二分之一波长谐振器由均匀阻抗传输线构成。在基膜谐振频率，图5(a)结构信号在P1端口与P2端口相位同(0°馈电)，图5(b)结构信号在P1端口与P2端口相位相反(180°馈电)。图中A为以馈电点为分界二分之一波长谐振器中较短的枝节，B为以馈电点为分界二分之一波长谐振器中较长的枝节。两个谐振器之间为电耦合，可以等效为电容。通过比较两种馈电结构P1端口与P2端口之间的导纳矩阵，可以看出，0°馈电结构比180°馈电结构额外多引入两个传输零点[11]。两个传输零点分别位于枝节A与枝节B为四分之一波长频率处。因此，设计的滤波器采用0°馈电结构，改善阻带特性。

图5 不同馈电方式的发夹型谐振器

3 滤波器仿真与测试结果

图6为设计的四级发夹型滤波器的实物照片。滤波器两侧为使用GSG探针对滤波器进行测量时探针接触的GSG PAD，PAD为接地共面波导结构(Coplanar Waveguide Ground，CPWG)，上层地与底层地通过金属化通孔进行连接。包含PAD在内，滤波器的尺寸为7 mm×4 mm，滤波器的核心面积为2.6 mm×2.5 mm(0.103λ0×0.099λ0)。

图6 滤波器实物照片

在测试之前，整个测试系统，包含矢量网络分析仪(Rohde&Schwarz，ZVA40)、射频电缆以及探针，采用Cascade MicrotechTM的标准基片，运用二端口LRRM(Line-Reflection-Reflection-Match)方法进行校准[16-17]。

图7为仿真的与实际测试的二端口S参数。图中方形符号曲线为ANSYSTMHFSS软件全波仿真的滤波器S参数结果，圆形符号曲线为实际测试的滤波器S参数结果。由测试结果与仿真结果的对比可知，滤波器的通带存在轻微的失谐，但是整体滤波器的响应与仿真结果一致性较好。滤波器响应共有四个传输零点，分别位于9.19 GHz、10.38 GHz、14.23 GHz和16.66 GHz，其中10.38 GHz与14.23 GHz两个传输零点由谐振器I与IV之间的交叉耦合引入，9.19 GHz与16.6 GHz两个传输零点则由0°馈电结构引入。滤波器中心频率为11.85 GHz，中心频率插入损耗为1.3 dB，带宽约为15 %。

图7 滤波器仿真与测试结果对比

4 结束语

设计了一款基于陶瓷基板的Ku频段四阶发夹型带通滤波器。对基于阶梯阻抗的小型化谐振器的特性进行了分析，通过合理设计滤波器版图实现交叉耦合，同时采用特定馈电结构引入额外的传输零点。所设计的带通滤波器具有四个传输零点，改善了滤波器的阻带特性，滤波器实际测试结果与仿真结果吻合较好。该设计方法在滤波器小型化以及提高阻带抑制度方面具有一定的应用价值。

[1] Zhang Y P,Sun M.Dual-band Microstrip Bandpass Filter Using Stepped-impedance Resonators with New Coupling Schemes [J].IEEE Transactions on Microwave Theory and Techniques,2006,54(10):3779-3785.

[2] Kuo J T.Compact Planar Quasi-elliptic Function Filter with Inline Stepped-impedance Resonators [J].IEEE Transactions on Microwave Theory and Techniques,2007,55(8):1747-1755.

[3] Zhang S B,Zhu L.Synthesis Design of Dual-band Bandpass Filters with λ/4 Stepped-impedance Resonators [J].IEEE Transactions on Microwave Theory and Techniques,2013,61(5):1812-1819.

[4] Makimoto M,Yamashita S.Compact Bandpass Filters Using Stepped Impedance Resonators [J].Proceeding of the IEEE,1979,67(1):16-19.

[5] Zhang L H，Yang X X，Ma Z W.Novel Millimeter-wave Ultra-wideband Filter Using Stepped-impedance Resonators [J].Radio Communications Technology,2013,39(3):53-56.

[6] Sagawa M,Makimoto M,Yamashita S.Geometrical Structures and Fundamental Characteristics of Microwave Stepped-impedance Resonators [J].IEEE Transactions on Microwave Theory Techniques,1997,45(7):1078-1085.

[7] Makimoto M,Yamashita S.Bandpass Filters Using Parallel Coupled Stripline Stepped Impedance Resonators [J].IEEE Transactions on Microwave Theory and Techniques,1980,28(12):1413-1417.

[8] Sagawa M,Takahashi K,Makimoto M.Miniaturized Hairpin Resonator Filters and Their Application to Receiver Front-end MIC’s [J].IEEE Transactions on Microwave Theory and Techniques,1989,37(12):1991-1997.

[9] Makimoto M,Sagawa M.Varactor Tuned Bandpass Filters Using Microstrip-line Ring Resonators [C]∥IEEE MTT-S International Microwave Symposium Digest,1986,86 (1):411-414.

[10] Hong J S,Lancaster M J.Theory and Experiment of Novel Microstrip Slow-wave Open-loop Resonator Filters [J].IEEE Transactions on Microwave Theory and Techniques,1997,45(12):2358-2365.

[11] Lee S Y,Tsai C M.New Cross-coupled Filter Design Using Improved Hairpin Resonators [J].IEEE Transactions on Microwave Theory and Techniques,2000,48(12):2482-2490.

[12] Zhao F,Dang Y L,Wang X.Design of Ka-band Microstrip Bandpass Filter on Ceramic Substrate [J].Radio Engineering,2012,42(3):61-64.

[13] Hong J S,Lancaster M J.Microstrip Filters for RF/Microwave Applications [M].USA:John Wiley & Sons,2004.

[14] Cameron R J.General Coupling Matrix Synthesis Methods for Chebyshev Filtering Functions [J].IEEE Transactions on Microwave Theory and Techniques,1999,47(4):433-442.

[15] Cameron R J.Advanced Coupling Matrix Synthesis Techniques for Microwave Filters [J].IEEE Transactions on Microwave Theory and Techniques,2003,51(1):1-10.

[16] Purroy F,Pradell L.New Theoretical Analysis of the LRRM Calibration Technique for Vector Network Analyzers [J].IEEE Transactions on Instrumentation and Measurement,2001,50(5):1307-1314.

[17] Liu S,Ocket L,Lewandowski A,et al.An Improved Line-Reflect-Reflect-Match Calibration with an Enhanced Load Model [J].IEEE Microwave and Wireless Components Letters,2017,27(1):97-99.