齿侧间隙对啮合力的动态影响分析

李 创，郗小鹏，吴宏宇，侯云雷

0 引 言

齿侧间隙（简称“侧隙”），是齿轮副非工作齿面之间的间隙。在精密传动系统中，侧隙是传动系统传动误差产生的主要因素之一，输入与输出之间理想的线性关系被打破，呈现间歇的非线性特征。

文献[1]研究表明侧隙导致伺服系统速度环开环频率特性降低；文献[2]利用Adams建立单自由度齿轮传动的动力学模型；文献[3]采用描述函数法处理侧隙的非线性，验证侧隙导致轴系扭转刚度的降低；文献[4]考虑时变啮合刚度，提出了二级齿轮传动的仿真实现技术与方法；文献[5]对含时变刚度和侧隙的多级齿轮传动的非线性动力学特性进行了分析，分析了动态啮合力随转速及啮合刚度变化的影响。

在上述文献的基础上，本文考虑侧隙及时变啮合刚度，建立二级齿轮传动的数学模型，利用虚拟样机技术，建立模拟复杂工况的动力学模型，重点研究了外界高频振动激励与非恒定负载力矩扰动下，相应参数对齿轮啮合力以及速度动态响应的影响，为传动系统平稳性和精确性的设计和优化提供参考。

1 动力学模型

1.1 齿轮传动简化模型

本文所指齿轮传动系统常见于机载或者车载目标跟随伺服系统和光电稳定系统等，一般具有以下特征：

a）系统具备高定位精度和动态响应特性，伺服带宽高；

b）适应复杂多变的随机叠加窄带或正弦的振动激励；

c）机械系统为多自由度系统，系统的谐振频率较高。

本文以某型号小型机载目标跟随伺服系统为研究依据，建立该系统的单轴齿轮传动模型，如图1所示，传动系统标准齿轮参数如表1所示。

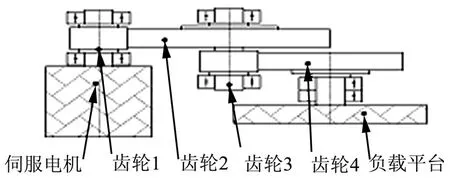
图1 单轴齿轮传动模型Fig.1 Single Axis Gear Transmission Model

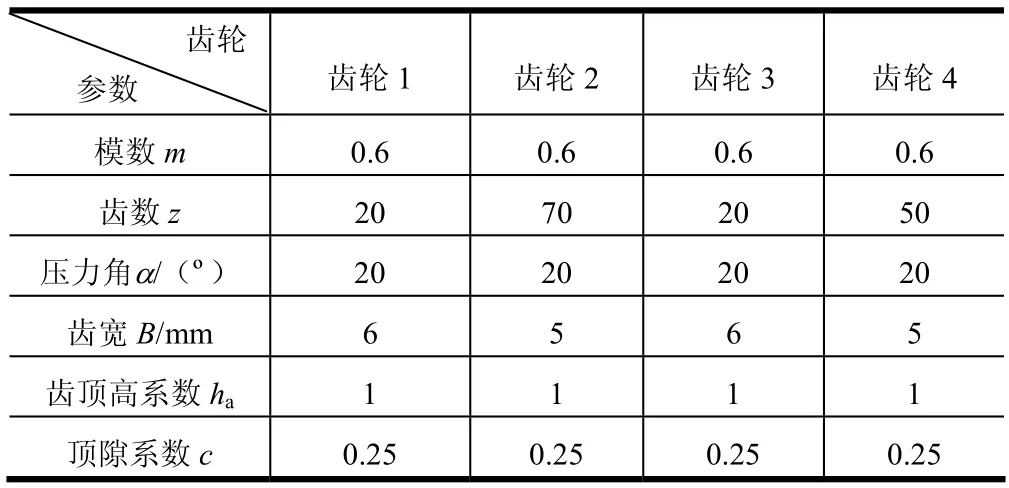
表1 标准齿轮参数Tab.1 Standard Gear Parameters

1.2 齿轮间隙的非线性特征

高频率的变向、加速使齿轮副在接触、分离、接触反复状态下，齿轮副等效的啮合弹性变形量呈现强非线性特征。

忽略齿轮精度和使用环境不同所造成的侧隙微小变化，对同一对齿轮副的侧隙均值处理。设齿轮副的侧隙为2bi，啮合线上的直线位移为 xi，则弹性变形量d ( xi)（i=1,2,3）的数学表达式如下：

1.3 含侧隙和时变啮合刚度多级齿轮动力学模型

本文重点研究在复杂多变的外部激励输入条件下，多级齿轮传动侧隙对系统动态特性和伺服性能的影响。适当简化齿轮动力学模型，采用文献[6]中的弹簧、阻尼和间隙的扭转-振动模型，如图2所示，同时考虑以下简化条件：

a）忽略轴端支撑的弹性变形和轴承游隙的影响；

b）忽略齿轮传动摩擦力的影响；

c）忽略因齿轮精度所引入的静态传递误差；

d）相互啮合的齿轮轴向固定，只存在扭转变形；

e）忽略由齿轮精度、使用环境等因素所造成的侧隙微小时变特征。

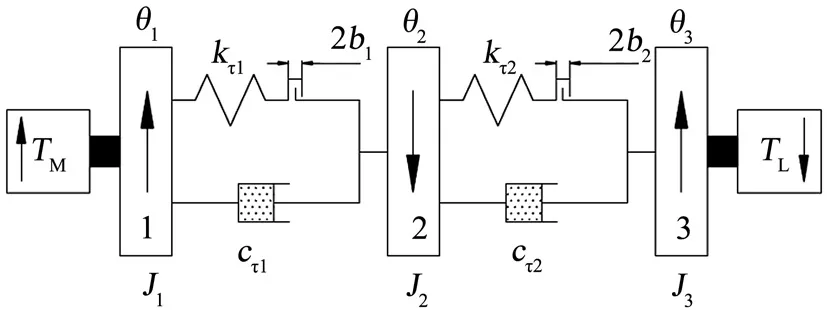
图2 二级齿轮动力学模型Fig.2 Secondary Dynamic Gear Model

扭转-振动非线性动力学数值分析，规定逆时针方向为正，采用集中质量法，建立其数学模型[6]。

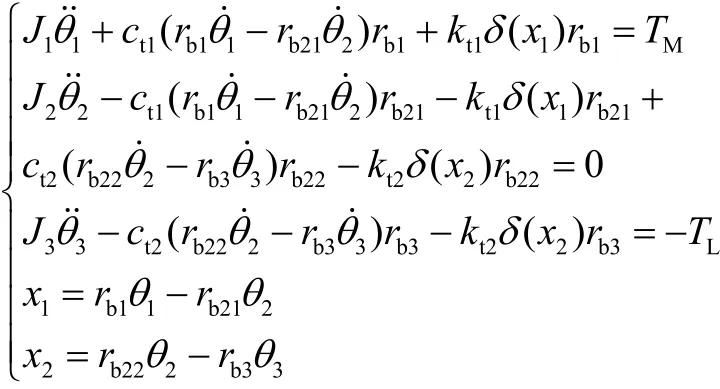
式中MT，LT分别为电机的驱动力矩和负载阻力矩；J1，J2，J3，J4为齿轮 1～4 的等效转动惯量；rb1，rb21，rb22，rb3为齿轮1、齿轮2、齿轮3和齿轮4的基圆半径；q1，q2，q3为齿轮的角位移；d(x1)，d(x2)为齿轮副的等效啮合弹性变形量；kt1，kt2为齿轮副的啮合刚度；ct1，ct2为齿轮副的啮合阻尼。

为便于扭转-振动模型的求解分析，建立多级齿轮传动动力学分析的矩阵形式表示为

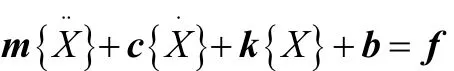
式中 m为质量矩阵；c为啮合阻尼矩阵；k为啮合刚度矩阵；b为与侧隙相对应的判定附加矩阵；f为负载矩阵。

由于侧隙的存在，齿轮在接触、分离和接触状态变换，∈ {- bi, 0,bi}，取值分别与3种状态相对应。

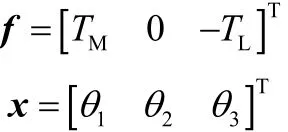
1.4 时变啮合刚度

齿轮在啮合过程中，单对齿啮合区和双对齿啮合区的周期性变化，导致齿轮副的啮合刚度呈现典型阶跃突变特性，如图 3所示。根据李润方、王建军等人的研究成果，在保证齿轮精度的前提下，啮合刚度具有明显的周期性变化。

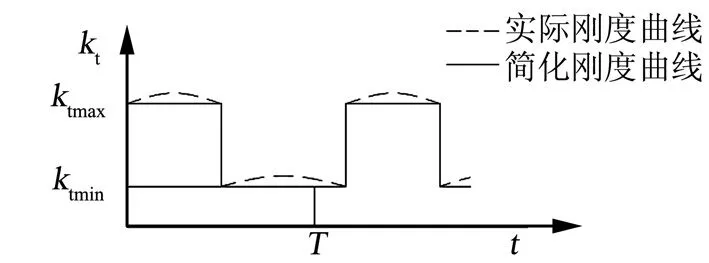
图3 时变啮合刚度简化曲线Fig.3 Curve of Time-varying Mesh Stiffness

按照图3所示，将齿轮啮合刚度简化为一个啮合周期的矩形方波函数：

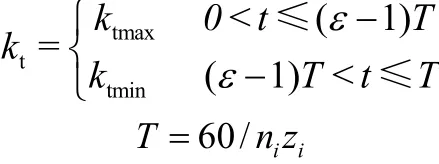
式中 ε为齿轮传动的重合度；T为啮合周期；in为第i个齿轮转速；iz为第i个齿轮齿数。公式以啮合频率进行傅里叶级数展开，保留一阶分量，则：

式中iw为第i对齿轮副的啮合频率；k0，a0，b0分别为展开式的常数项、一阶余弦项和一阶正弦项。

轮齿的啮合阻尼可按下式计算，按照 Kasuba[7]和Wang[8]的分析计算，一般为0.03～0.17，本文ix=0.07。

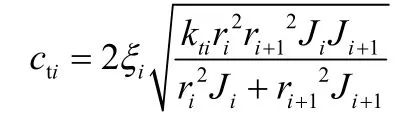
1.5 侧隙与传动特性的影响分析

对于标准的渐开线圆柱齿轮传动，侧隙的存在使齿厚减小，啮合的平均刚度降低，平均刚度与传动角速度变化曲线如图4所示，其中，侧隙为2d，平均啮合刚度为vK。

图4 平均刚度与传动角速度变化曲线Fig.4 Variation Curve of Sitiffness and Angular Velocity

在随机振动叠加冲击的工况环境下，系统的载荷输出呈现高频的交变特征，侧隙附加的冲击振荡会导致系统动力输入波动显著增加，超越系统的动态适应能力，导致系统失稳。

2 系统仿真

2.1 系统仿真分析模型

根据上述理论分析，明确含侧隙齿轮传动动力学模型中刚度、阻尼以及负载的矩阵函数，利用 Adams动力学仿真软件中的齿轮传动仿真模块，首先建立其与之符合的实体模型，设置齿轮副的啮合刚度，阻尼和侧隙值，基于Impact函数的接触力计算，分析模拟载体的高频正弦激励和齿轮系统本身正弦激励条件下齿轮啮合力和齿轮输入的力矩波动响应，为具有高动态响应的随动系统的传动设计提供理论支撑。仿真模型如图5所示，简化的二级齿轮传动系统，包含振动载体、齿轮接触副和边界约束条件等。其中，接触类型为实体接触，刚度系数取决于碰撞物体的材料和结构形式，可近似按照文献[9]确定，碰撞系数取值1.5，最大阻尼系数设为刚度系数值的0.5%，穿透深度取值0.1 mm，仿真参数设置中忽略齿轮传动摩擦影响。

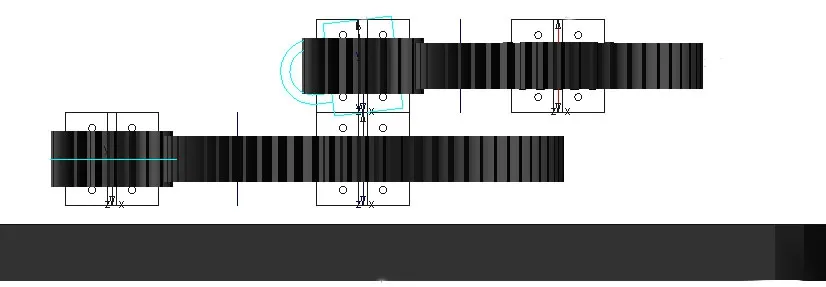
图5 仿真模型Fig.5 Simulation Model

2.2 定载荷下齿轮啮合特性仿真分析

首先分析定载荷、恒速运动工况，验证齿轮啮合模型的准确性和实用性。

齿轮1输入转速500 r/min。为避免速度突变，对仿真结果的影响，采用平滑加速函数step(t i me, 0,0,0.2,3000d)实现速度的控制。传动输出端齿轮 4施加恒定负载 1.5 N·m，采用平滑加速函数step( ti me , 0 , 0 , 0.2 , 15000 )施加力矩。

根据1.4节时变啮合刚度的分析表明，齿轮1和齿轮2的啮合呈现时变特征，啮合频率为1047.197 rad/s。仿真分析得到的齿轮啮合力时域和频域分别如图 6和图7所示。

总而言之,胫骨平台合并半月板损伤患者接受早期的胫骨平台骨折手术修复治疗,对损伤半月板进行修复,能够在一期就实现愈合,避免了骨折预后创伤性关节炎的发生,临床中效果比较突出,值得推广使用。

图6 定载啮合力的时域Fig.6 Time-Domain Chart of Fixed Meshing Force

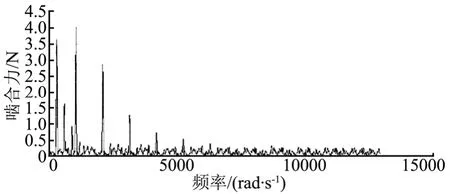
图7 定载啮合力的频域Fig.7 Frequency-Domain Chart of Fixed Meshing Force

从时域图可以看出齿轮啮合典型的时变特征，频域图得到啮合主频率为1046.57 rad/s，与理论分析相互吻合，验证了齿轮啮合模型理论分析的正确性。

2.3 侧隙对啮合力的仿真分析

a）侧隙影响的仿真分析。

重点研究侧隙对齿轮啮合力和啮合速度的影响。为简化仿真计算量，选取末级单自由度齿轮传动（齿轮3和齿轮4），同时增加齿轮4的偏心质量，模拟负载。齿轮3输入速度正弦激励，齿轮4为从动轮。齿轮系统的振动给定激励，可以模拟随机振动、正弦冲击等复杂工况条件。侧隙通过改变齿轮副的中心距进行侧隙数值模拟，设定为0 mm、0.1 mm、0.16 mm 3个量值。兼顾计算的准确性和效率，采用 GSTIFF的刚性积分器，可以避免Jacobian矩阵病态的SI2格式。单级齿轮系统仿真模型如图8所示。

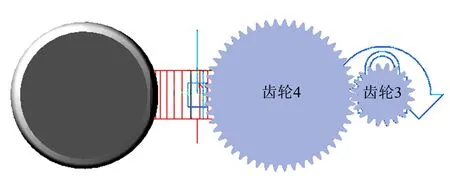
图8 侧隙仿真模型Fig.8 Backlash Simulation Model

速度正弦激励信号的幅值为 0.5 m/s，角频率为1000 rad/s。齿轮输入端（齿轮3）的输入为速度正弦激励信号幅值为1000 (°)/s，角频率为10 rad/s。信号曲线如图9所示。

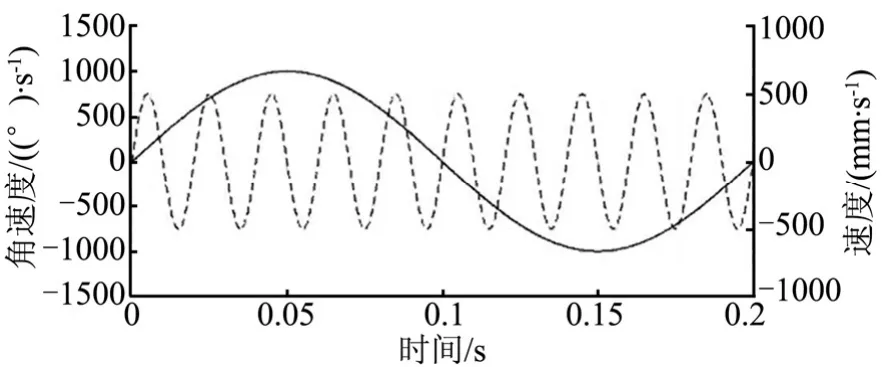
图9 激励信号曲线Fig.9 Excitation Signal Curve

分别研究不同侧隙量情况下的齿轮啮合力的动态响应，分析时域和频域特征。仿真结果表明，齿轮啮合力会伴随振动激励出现周期性的峰值力和角速度的跳变，而且随着侧隙的增大，啮合力呈现大幅度的增长，速度波动也愈明显，甚至造成传动系统的失稳。不同侧隙情况下啮合力时域对比曲线、啮合力频域对比曲线和角速度对比曲线分别如图10～12所示。

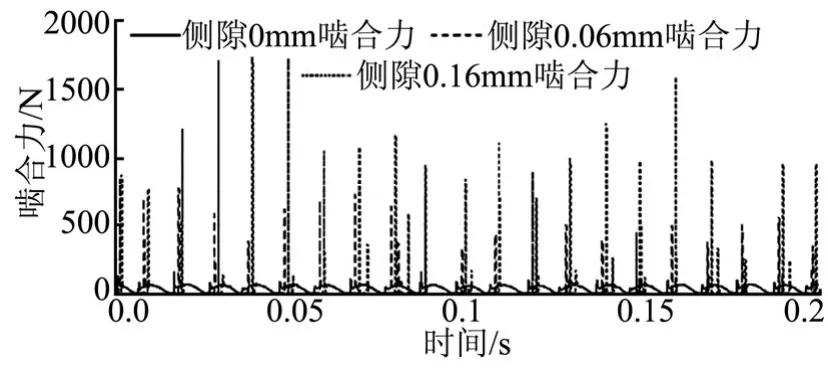
图10 不同侧隙啮合力时域对比曲线Fig.10 Time-Domain Curve of Different Meshing Force

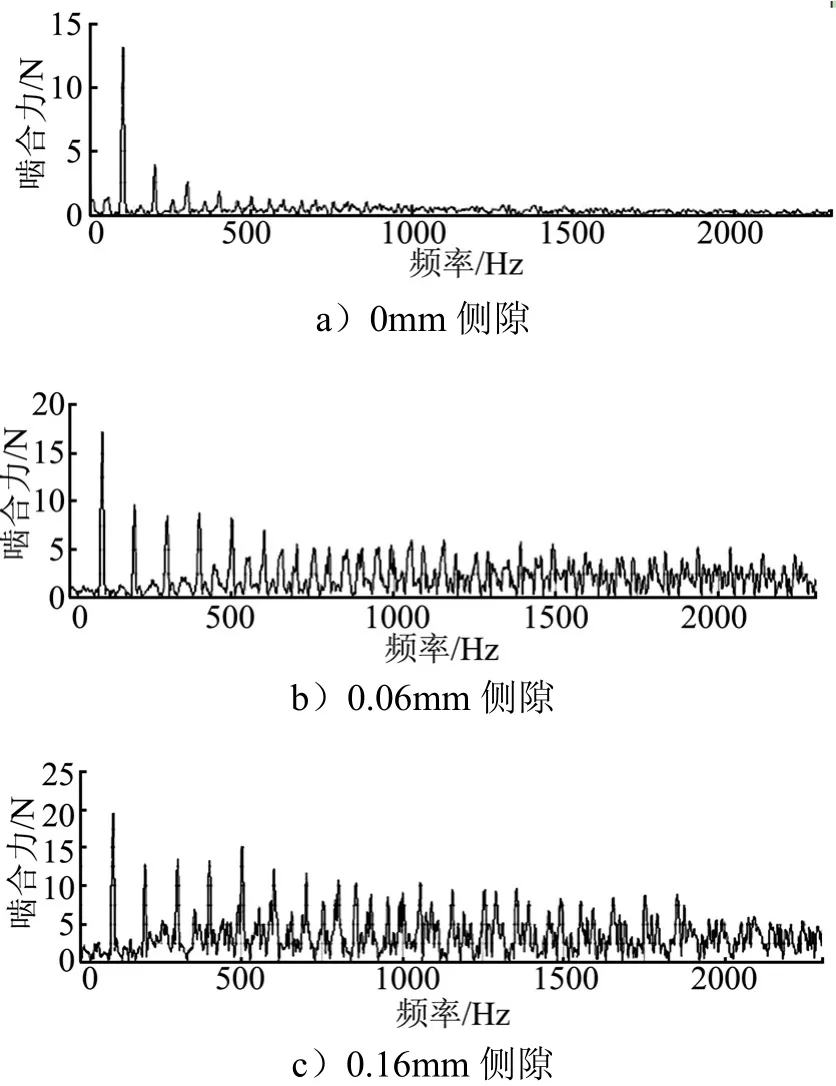
图11 不同侧隙啮合力频域对比曲线Fig.11 Frequency-Domain Curve of Different Meshing Force

图12 不同侧隙角速度对比曲线Fig.12 Angular Velocity of Different Backlash

b）负载偏心影响的仿真分析。

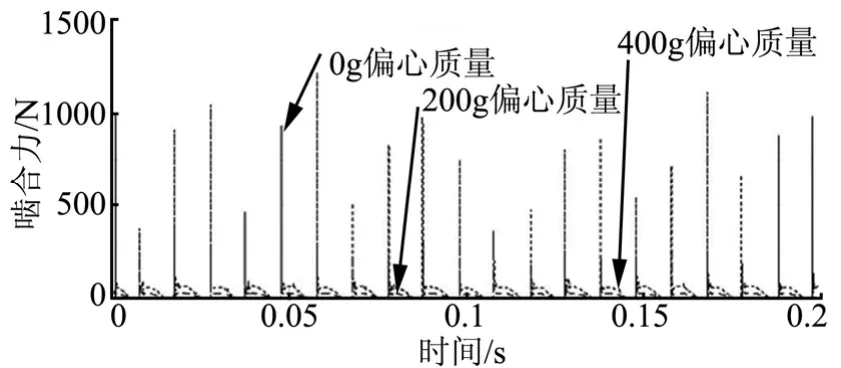
图13 不同偏心啮合力对比曲线Fig.13 Meshing Force Curve of Different Eccentricity

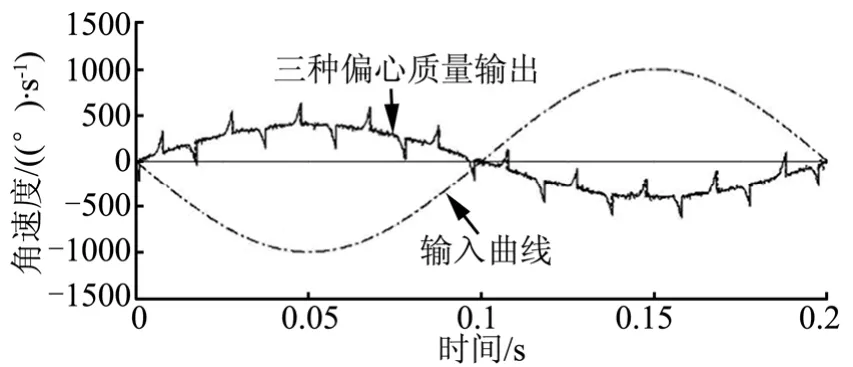
图14 不同偏心角速度对比曲线Fig.14 Angular Curve of Different Eccentricity

因此过大的齿侧间隙，会使传动系统振动加剧，在高频振动激励下，齿轮由于啮合的冲击震荡导致的附加动载荷和速度的波动显著增加，当间隙增加到一定程度，容易引起系统共振，造成驱动过载，导致系统运动失衡、随机性的卡滞、堵转和噪声，影响系统的平稳性、可靠性和寿命。同时在传动系统设计中，尽量减小偏心质量和偏心量，可以降低力矩突变。

3 结 论

本文根据齿轮的扭转-振动理论，建立含侧隙和时变啮合刚度的二级齿轮传动系统的数学模型，建立了高频正弦振动激励和往复速度给定的Adams动力学仿真模型。根据仿真分析，得出如下结论：

a）高频振动激励下，侧隙导致齿轮啮合的冲击振荡，引起额外附加动载荷，量级会随着偏心质量和偏心量的增加呈现大幅度的增长，提高传动系统末级减速比，消除末级齿隙，从而实现对传动系统回差的细分，减小动载荷对输入稳定性的影响；

b）速度输出伴随振动激励频率出现周期性的速度阶跃，侧隙愈大，速度波动幅值愈大，在高精度定位和精确速度控制环路中，尽量实现0侧隙传动，避免冲击激励下的速度阶跃；

c）大惯量的偏心负载是引起齿轮传动的振动、冲击和噪声的主要原因之一，减小偏心质量和偏心量可以显著抑制齿轮传动中啮合力和速度的周期性阶跃。

[1] 周金柱, 段宝岩, 黄进. 含有齿隙伺服系统的建模与对开环频率特性的影响[J]. 中国机械工程, 2009(14)： 1722-1726.

Zhou Jinzhu, Duan Baoyan, Huang Jin. Modeling and effects on open-loop frequency for servo system with backlash[J]. China Mechanical Engineering, 2009(14)： 1722-1726.

[2] 洪清泉, 程颖. 基于ADAMS的多级齿轮传动系统动力学仿真[J]. 北京理工大学学报, 2003, 23(6)： 690-693.

Hong Qingquan, Cheng Ying. Dyamic simulation of multi-stage gear train system in adams[J]. Transactions of Beijing Institute of Technology, 2003,23(6)： 690-693.

[3] 谢晓燕. 伺服系统的消隙抑振研究[D]. 南京： 南京理工大学, 2008.

Xie Xiaoyan. Study on backlash eliminator of servo system[D]. Nanjing University of Science and Technology, 2008.

[4] 唐增宝, 钟毅芳, 刘伟忠. 多级齿轮系统的动态仿真[J]. 机械传动,1993, 17(1)： 37-41.

Tang Zengbao, Zhong Yifang, Liu Weizhong. Dynamic simulation study on Muti-stage gear system[J]. Mechanical Transmission, 1993, 17(1)：37-41.

[5] 胡鹏, 路金昌, 张义民. 含时变刚度及侧隙的多级齿轮系统非线性动力学分析[J]. 振动与冲击, 2014, 33(15)： 150-156.

Hu Peng, Lu Jinchang, Zhang Yimin. Non-linear dynamic feature analysis of a multi-stage gear system with time-varying mesh stiffness and backlash[J]. Journal of Vibration and Shock, 2014, 33(15)： 150-156.

[6] 朱燕芬, 陈恩利, 申永军, 等. 含有故障的齿轮系统扭转振动分析[J].北京机械工业学院学报, 2007, 22(4)： 44-48.

Zhu Yanfen, Chen Enli, Shen Yongjun, et al. Analysis of torsional vibration of a spur gear system with faults[J]. Journal of Beijing Institute of Machinery, 2007, 22(4)： 44-48.

[7] Kasuba R, Evans J W. An extended model for determining dynamic loads in spur gearing[J]. Journal of Mechanical Design, 1981, 103(2)： 398-409.

[8] Wang K L, Cheng H S. A numerical solution to the dynamic load, film thickness and surface temperature in spur gears[J]. Journal of Mechanical Design, 1981, 103(1)： 177-187.

[9] 龙凯, 程颖. 齿轮啮合力仿真计算的参数选取研究[J]. 计算机仿真,2002, 19(6)： 87-88, 91.

Long Kai, Cheng Ying. Study on parameters of gear mesh force simulation[J]. Computer Simulation, 2002, 19(6)： 87-88, 91.