天基单星测角跟踪条件下的空间非合作目标定轨
张雪敏 李 萌 熊 超
1.西安思源学院,西安 710038 2.西安航天天绘数据技术有限公司,西安 710010 3.千寻位置网络有限公司, 上海 200433
空间非合作目标(Non-cooperative Space Target,NCST)是泛指一类不能提供有效合作信息的空间物体,包括故障或失效卫星、空间碎片以及敌方航天器等[1]。天基空间目标监视在测控覆盖率、多目标测控能力、以及运营成本等方面具有较大优势,可以克服传统地基空间目标监视系统的缺陷,它既可与地基系统互为补充,又可自成体系。此外,天基观测站可以根据任务需要进行变轨跟踪,极大地增加了空间态势感知能力;微小卫星技术的发展也为天基分布式探测监视的实现提供了支持,降低了天基监视的门槛[2-3]。因此,利用天基观测平台实现对空间目标的跟踪定轨将是未来发展的趋势。
尽管美国掌握了强大的地基空间目标监视能力,但仍不惜重金打造其天基空间目标监视系统(Space Based Space Surveillance,SBSS)[4-5]。SBSS 系统是一个低地球轨道光学遥感卫星星座,由3~8颗载有光电敏感器的卫星组成星座,设计寿命5 年,能够实时跟踪空间目标;另外,英国、日本和德国等发达国家也开展了相关技术研究。国内对空间碎片的研究起步较晚,以地面展开。
在天基观测平台上获取目标观测信息的方式包括有源主动和无源被动2种工作方式[2,6]。其中,采用光电传感器的无源工作方式隐蔽性好、作用距离远,具有重大实用价值,但这种方式只能获得目标的角度测量信息。因而,天基仅测角条件下空间非合作目标的无源跟踪定轨方法及其相关技术已成为近年来的研究热点。如文献[1]提出了一种遍历切割平面的初轨确定方法,能快速准确地为轨道改进提供历元初值;文献[7]针对轨道改进中的迭代发散和收敛于局部极小点的问题,提出了选取多个迭代初值进行轨道改进的采样方法;文献[8]提出基于剖分节点优选的约束微分修正方法,利用两个短弧测量实现对新发现目标的初轨确定,但并未提及数据关联问题;文献[9]针对太阳同步轨道监视卫星对GEO目标跟踪监视问题进行了仿真分析;文献[10]分析了编队卫星跟踪空间目标的初定轨问题。上述研究采用仿真计算的手段进行了验证,都得出了较为理想的定轨结果。事实上,目前国内鲜见报道天基非合作目标跟踪定轨的实测数据分析。
在实际应用中,受卫星姿态控制、照相机安装及跟踪模式限制[10],天基跟踪平台往往难以获取理想跟踪效果(如文献[9]得出的每圈5min的跟踪弧段,实际工程中往往只能获取1~2min超短弧数据);另外,理想的编队跟踪方式[1,11]在短期内尚未工程实现。目前,利用天基单星平台跟踪监视空间目标将是天基系统发展初期的主要应用方式之一。因而,利用单星超短弧测角观测数据确定空间非合作目标的轨道仍是其中的关键问题,尚需开展大量研究和试验验证。
针对天基单星测角跟踪条件下的空间非合作目标定轨问题,考虑空间目标天基跟踪观测约束条件,建立了基于测角观测数据的定轨模型,并针对实际工程约束下的超短弧测角观测数据开展定轨试验,分析超短弧仅测角数据定轨的收敛性和精度。
1 空间目标可探测条件
在天基光学监视系统跟踪模式下,空间目标可见性条件除了受地球等天体遮挡影响外,还要满足光电传感器的成像条件;其监视范围受2种因素影响:1)空间几何因素;2)光学因素。其中光学因素较复杂,涉及到目标辐射强度的计算及考虑背景亮度等因素,两者交集为天基光电传感器的可见性区域[12-13]。
1.1 空间几何可见
对于近地空间环境,空间几何因素即地球遮挡约束,是指地球遮挡住观测平台对空间目标观测视线的情况。地球遮挡不仅会影响光电传感器观测,对于其它观测设备也有阻碍作用,虽然可以采用卫星中继等手段解决,但会大大影响观测精度。地球遮挡约束下观测平台对目标的空间几何可见情况如图1所示。
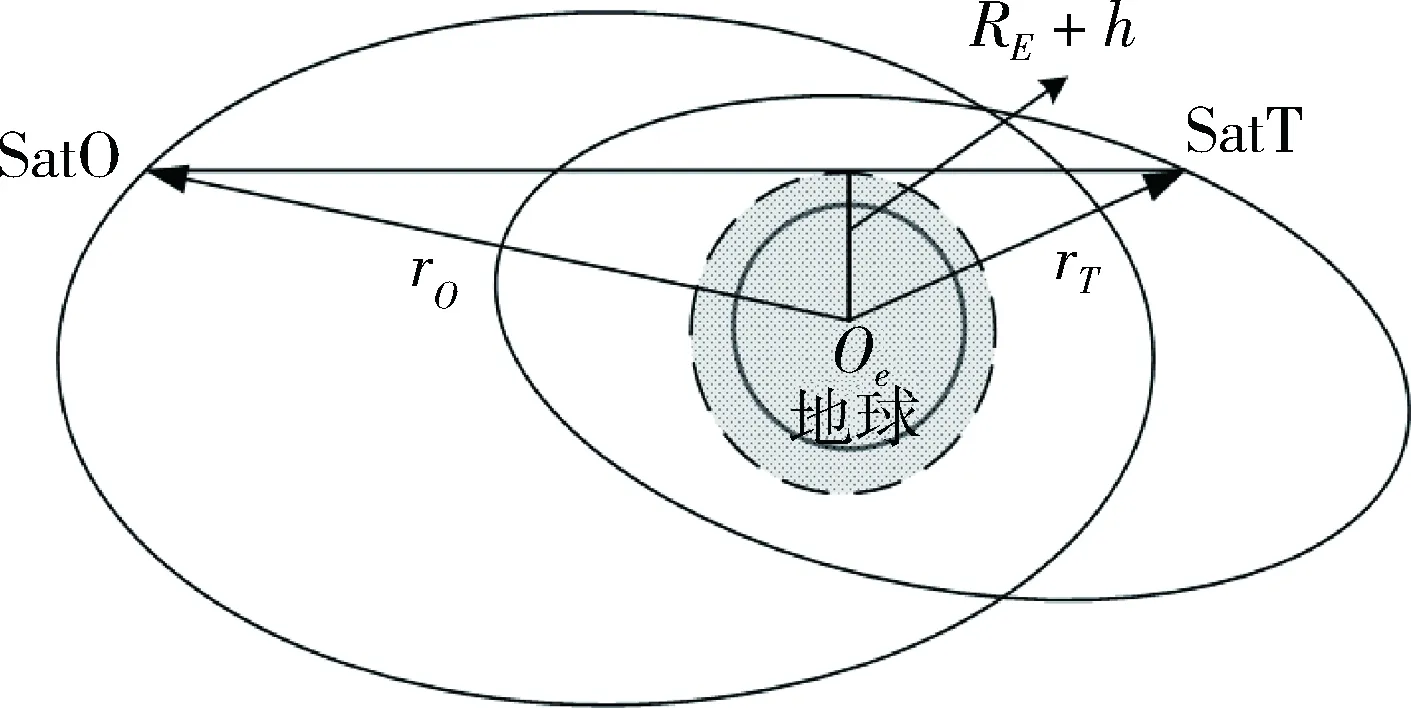
图1 地球遮挡约束下观测平台对目标可见性
计算地球遮挡约束需要同时考虑观测平台SatO和目标SatT的运行轨道,rO,rT分别为历元tk下观测平台和空间目标在地心赤道惯性坐标系下的位置矢量,取地球赤道半径为RE,地球稠密大气层高度为h,则观测平台对目标的观测视线被地球遮挡条件为:
(1)
欲求地球遮挡约束下的历元tk,需要把B表示为tk的函数B(tk),并分析求解B(tk)=0。已知二体理论下,空间目标的轨道根数为a,e,i,Ω,ω,f(M),则rT可以表示为:
rT=rTcosf·P+rTsinf·Q
(2)
其中:
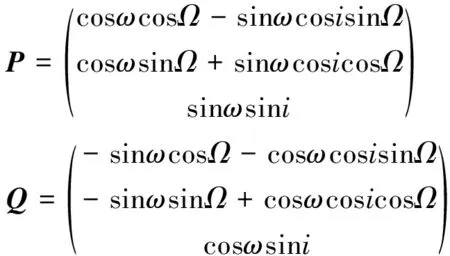
而f可以由M近似表示为:
(3)
其中:M=n(t-τ);n为平均角速度;τ为过近地点时刻。
由式(1)~(3)可计算地球遮挡约束函数B(tk)。采用牛顿迭代法求解B(tk)=0,从初始历元t0快速得到地球遮挡历元tk,然后判断B(tk+Δt)的符号。若B(tk+Δt)>0,则历元tk为地球遮挡结束时刻,否则为遮挡开始时刻;若在设定迭代次数内无收敛解,说明历元t0附近没有地球遮挡,重新选择初始历元t0进行迭代求解。牛顿迭代法要用到B(tk)对历元tk的导数:
(4)
其中:
1.2 光学可见
光学可见定义为空间目标在光学设备观测视场内,目标状态所能满足天基光学设备的成像条件[13-14](主要是空间目标的光照强度和天光背景)。首先判断能否满足基本的光照条件,然后根据空间目标的辐射照度判断能否成像。为便于说明,图2给出了太阳与地球空间几何关系示意图(图中A为太阳直射区,B为斜射区,C为地影区)。
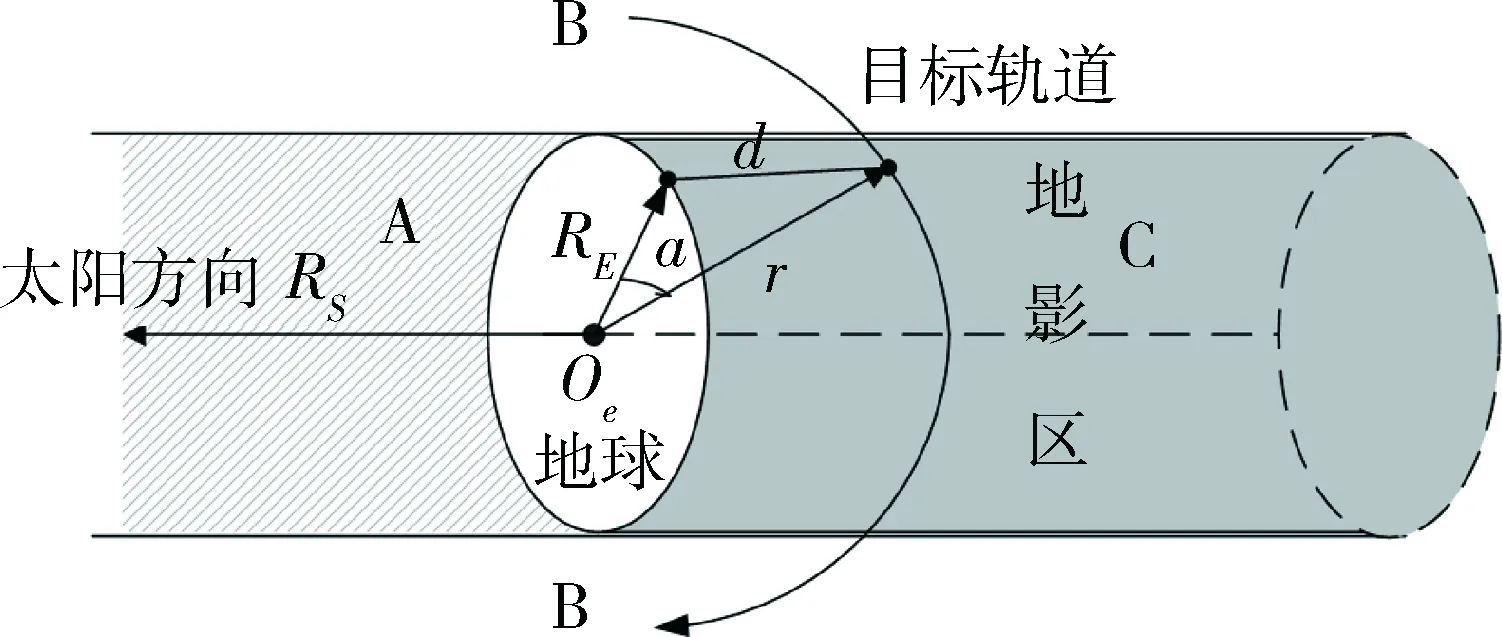
图2 柱形地影区的空间几何关系
则天基光学设备无法观测空间目标的情况为:1)空间目标在地影区内(可以红外成像);2)空间目标在光学设备视场内,但背景是太阳,由于背景过亮无法识别目标;3)空间目标在光学设备视场内,但背景是太阳直射的地球,由于背景过亮无法识别目标。
按照空间几何可见和光学可见2种判别方法,分别计算出空间几何可见区域和光学可见区域,则两者交集为天基光学设备可观测空间目标的区域。
2 天基单星测角轨道改进
利用天基单星的测角观测确定空间非合作目标的轨道是一个参数估计过程,采用较为精确的动力学模型和合适的参数估计方法,可以获得比初定轨更加精确的空间目标轨道,又称轨道改进。
2.1 定轨算法
设ti时刻的观测量为Yi,状态向量为xi,G(xi,ti)是观测数据Yi对应的真值,有
Yi=G(xi,ti)+εi
(5)
εi是Yi的随机噪声,也就是说,实际观测值Yi是其真值G(xi,ti)和测量噪声εi的线性函数。状态向量满足:

(6)
x(t0)=x0
(7)
空间目标在ti时刻的状态矢量xi与某历元t0时刻的状态矢量x0存在某种函数关系:
x=Φ(t,t0)x0
(8)
其中,Φ(t,t0)为t0时刻到t的状态转移矩阵。
(9)
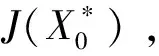
(10)
满足最佳估值的条件成为:
(11)
即:
(12)
则加权最小二乘法的最佳估值:
(13)
2.2 星间测角观测模型
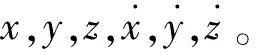
因此:
3 定轨实验及精度分析
3.1 定轨数据及策略
针对某低轨天基平台对同步带目标开展跟踪和定轨试验,为分析监视能力和定轨精度,选取了多颗同步带合作目标开展试验。低轨平台自身的轨道是确定非合作目标轨道的空间基准,搭载有单频GPS接收机,因此采用多星联合定轨策略,同时估计低轨卫星(LEO1)和目标星(本文选取GEO1、GEO2)的轨道参数。其中对低轨平台估计1个大气阻力因子,目标卫星估计1个太阳光压因子,观测数据包括平台GPS自定位数据(x,y,z)和目标星的天基光学测角观测数据(赤经、赤纬),数据加权方式如下:
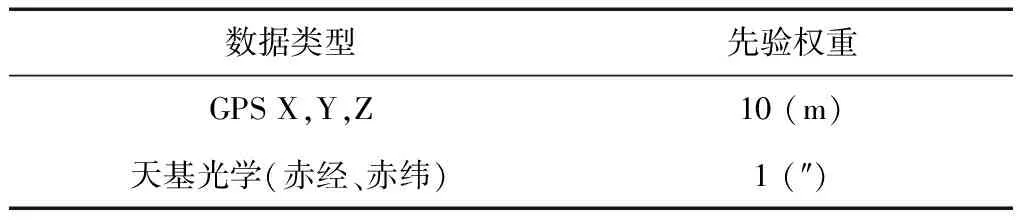
表1 数据先验权重
在跟踪试验中,光学相机固定安装于天基平台的某轴,以扫描方式快速扫过同步带,受多种探测条件限制(第1节),对同一目标的单个有效观测弧段仅2~3min,3天左右能够完成对同一目标的2次重复观测。本文采集了7天弧段内2个GEO目标的超短弧稀疏观测数据,其中某段数据质量和使用情况见表2。

表2 某段天基数据情况
3.2 单个超短弧天基数据定轨分析
由于单个短弧段的赤经和赤纬序列随时间变化近似线性,已有分析表明,单个平台对空间目标天基光学测角定轨可观度差,定轨易收敛到局部极小点或者发散。下面利用实测数据进行计算分析。由于试验中跟踪的目标航天器均为合作目标,因此可以利用其它合作式跟踪技术获得精确的目标轨道,称为“实际轨道真值”。
CASE1:初轨半长轴采用实际轨道真值;
CASE2:初轨半长轴采用实际轨道真值+100km;
CASE3:初轨半长轴采用实际轨道真值-100km。
从上述2组试验结果看,使用一个超短弧段天基数据定轨,给定半长轴±100km范围内的初值,定轨结果均收敛到某固定偏差值,难以收敛到正确结果。其原因是单个超短弧测角跟踪几何约束太差,定轨系统呈弱可观性,试验结果进一步验证了文献[7]的理论分析结果。

表3 GEO1单弧段天基数据定轨精度

表4 GEO2单弧段天基数据定轨精度
3.3 两个超短弧天基数据定轨分析
从上述结果可得,使用单个超短弧天基光学数据定轨难以收敛到较小误差范围,下面分析两段天基数据的定轨精度。
试验I:使用了主星GPS数据、目标星GEO1仅天基观测数据,定轨区间3.3天,取初轨半长轴误差20km。定轨结果见表5~7。

表5 GEO1两段短弧天基数据使用情况

表6 GEO1两段短弧天基数据定轨精度(轨道根数)

表7 GEO1两段短弧天基数据定轨精度(J2000.0坐标系位置速度)
结果表明半长轴误差51.676m,位置误差约20km。
试验II:GEO1星,两段超短弧天基数据,分析不同初轨误差的定轨结果。
CASE1:初轨半长轴采用实际轨道真值;
CASE2:初轨半长轴采用实际轨道真值+100km;
CASE3:初轨半长轴采用实际轨道真值-100km。

表8 GEO1两段短弧天基数据定轨精度
试验III:针对GEO2星,采用两段超短弧天基数据、不同初轨误差的定轨结果。
CASE1:初轨半长轴采用实际轨道真值;CASE2:初轨半长轴采用实际轨道真值+50km;CASE3:+80km;CASE4:+100km;CASE5:-100km;CASE6:-250km;CASE7:-300km;CASE8:初轨半长轴采用表4给出的单圈数据定轨结果。
从上述定轨结果来看,采用两段超短弧天基测角数据定轨,在大多情况下可以收敛,半长轴精度约100m,且:
1)当其它轨道参数较为精确时,半长轴100km误差范围内可收敛至100m;
2)当升交点赤经误差较大时(约37°),半长轴100km误差范围内可收敛至100m。
4 结论
针对天基单星测角跟踪条件下的空间目标定轨问题,分析了空间目标的工程可探测条件,建立了低轨监测星对中高轨非合作式光学跟踪测量模型和多目标定轨模型,开展了低轨监视卫星跟踪监视同步带群目标的定轨试验,针对天基超短弧单星仅测角定轨的收敛性和精度展开分析,结果表明,利用单个超短弧天基测角数据定轨易收敛至存在固定偏差的某一局部极小值;采用两段超短弧实测数据定轨,在较大的初值误差条件下均可以收敛,半长轴精度约100m、位置精度约20km。本文的研究结果可以为天基空间目标监视技术的应用提供一定的参考。
参 考 文 献
[1] 潘晓刚,李济生,段晓君,周海银. 天基空间目标监视与跟踪系统轨道确定技术研究[J]. 自然科学进展. 2008, 18(11): 1226-1239.(Pan Xiaogang, Li Jisheng, Duan Xiaojun, Zhou Haiyin. Space-based Space Surveillance and Tracking System Orbit Determination Technology Research [J]. natural science progress. 2008,18(11): 1226-1239.)
[2] 谭莹. 天基空间目标探测技术探讨[J]. 空间电子技术,2006,3(3):5-9.(Tan Ying. Exploration of Space-based Space Target Detection Technology for [J]. Space Electronics, 2006,3(3):5-9.)
[3] 乔凯,王治乐,丛明煜. 空间目标天基地基监视系统对比分析[J]. 光学技术,2006,32(6): 744-749.(Qiao Kai, Wang Zhile, Cong Mingyu. Analysis on Space Based and Ground Based Surveillance System to Space Target[J].Optical Technique, 2006, 32(6): 744-749.)
[4] Sharma J,Stokes GH. Von Braun Curt,et a1. Toward Opera-Tional Space-Based Space Surveillance [J]. Lincoln Laboratory Journa1,2002,13(2): 309-313.
[5] 崔潇潇. 美国天基空间目标监视系统[J]. 国际太空,2011,(7): 37-43.(Cui Xiaoxiao. The U.S. Space Surveillance System [J]. International Space, 2011, (7): 37-43.)
[6] James D Rendleman, Robert E. Ryals. Spacecraft Operator Duty of Care[C]. AIAA Space 2011 Conference and Exposition,2011.
[7] 李冬,易东云,程洪玮. 天基空间目标监视的短弧段定轨技术[J]. 宇航学报, 2011, 32(11): 2339-2345. (Li Dong, Yi Dongyun, Cheng Hongwei. Short arc Segment Setting Technology for Target Monitoring in Space-based space[J]. Journal of Astronautics, 2011, 32(11): 2339-2345.)
[8] 李骏,安玮,周一宇. 天基光学短弧初轨的约束微分修正方法[J]. 宇航学报, 2009, 30(2): 769-774.(Li Jun, An Wei, Zhou Yiyu. Constraint Differential Correction in Initial Orbit Determination with Short Arcs in Optical Space-based Space Surveillance[J].Journal of Astronautics, 2009, 30(2): 769-774.)
[9] 王秀红,李俊峰,王彦荣.天基照相机监测空间目标定轨方法及精度分析[J]. 光学精密工程, 2013, 21(6): 1394-1403.(Wang Xiuhong, Li Junfeng, Wang Yanrong. Space-based Camera Monitoring Space Target Orbit Determination Method and Precision Analysis [J]. Optical Precision Engineering, 2013, 21(6): 1394-1403.)
[10] 周美江, 朱振才, 杨根庆,等. 天基光学同步带目标监视跟踪模式[J]. 中国空间科学技术, 2015, 32(3):35-43.(Zhou Meijiang, Zhu Zhencai, Yang Genqing, et al. Space-based Optical Synchronization Band Target Monitoring and Tracking Mode [J]. China Space Science and technology, 2015, 32(3): 35-43.)
[11] 刘光明,廖瑛,文援兰,等. 基于双星编队的空间非合作目标联合定轨方法[J]. 宇航学报. 2010, 31(9): 2095-2100.(Liu Guangming, Liao Ying, Wen Yuanlan, et al. The Joint Orbit Determination Method of Space Non Cooperative Target Based on Double Star Formation [J]. Journal of Astronautics. 2010, 31(9): 2095-2100.)
[12] 李骏, 安玮, 周一宇. 基于天基光学监视的空间目标跟踪方法研究[J]. 空间科学学报, 2009, 29(3):326-331.(Li Jun, An Wei, Zhou Yiyu. Research on Space Target Tracking Based on Space-based Optical Surveillance Research [J]. Journal of Space Science, 2009, 29(3): 326-331.)
[13] 赵砚, 易东云, 潘晓刚,等. 基于天基光学观测的空间目标可见性分析[J]. 飞行器测控学报, 2007, 26(3):5-12.(Zhao Yan, Yi Dongyun, Pan Xiaogang, et al. Spatial Object Visibility Analysis Based on Space-based Optical Observation [J]. Aircraft Measurement and Control Journal, 2007, 26(3): 5-12.)
[14] 盛卫东. 天基光学监视系统目标跟踪技术研究[D]. 国防科学技术大学, 2011.(Sheng Weidong. Space-based Optical Surveillance System Tracking [D]. National Defense Science and Technology University, 2011.)
[15] 赵博, 周庆勇, 张旺,等. 基于天地基测控的空间目标联合定轨研究[J]. 光电工程, 2011, 38(11):57-62.(Zhao Bo, Zhou Qingyong, Zhang Wang, et al. Research on Joint Orbit Determination of Space Target Based on Space-based Measurement and Control [J]. Opto-Electronic Engineering, 2011, 38 (11): 57-62.)

