导航定位过程中的一种高效卫星组合选取策略

丰泽斌 马龙华 朱国杰

1.国家开发银行辽宁省分行，沈阳 110014 2.浙江大学宁波理工学院，宁波 315100 3.浙江大学， 杭州 310027

无论是在实际应用还是仿真平台实验过程中，导航定位都涉及到在可见卫星中选星的过程，传统的选星算法运算过于复杂，对此，国内外就如何改进选星过程做了很多研究，Bo Wang、Shunting Wang[1]等人提出用GPS姿态确定的改进选星算法，M.R. Masavi[2]提出用遗传算法更加准确高效地选星, Miaomiao Wei、 Ju Wang[3-4]等人通过重新选择删除的卫星以及利用卫星的比较以及分布特征改进了准最佳选星法，Miaoyan Zhang和Jun Zhang[5]提出了利用可见卫星子集选星的一种新的准最佳选星方案，还有基四选星算法[6]，基于加权行列式的选星算法[7]等。本文针对传统选星法的问题提出自己的一系列解决方案。

1 卫星选择策略

为了实现选星策略的高精度和高效率，本文主要关注可选卫星的仰角、信号质量以及几何分布因子的相关信息。

1.1 卫星的仰角选择

首先考虑可见卫星的仰角信息，在东北天地理坐标系中，假设有一载体位置为A，卫星位置为B，其位置情况如图1所示：

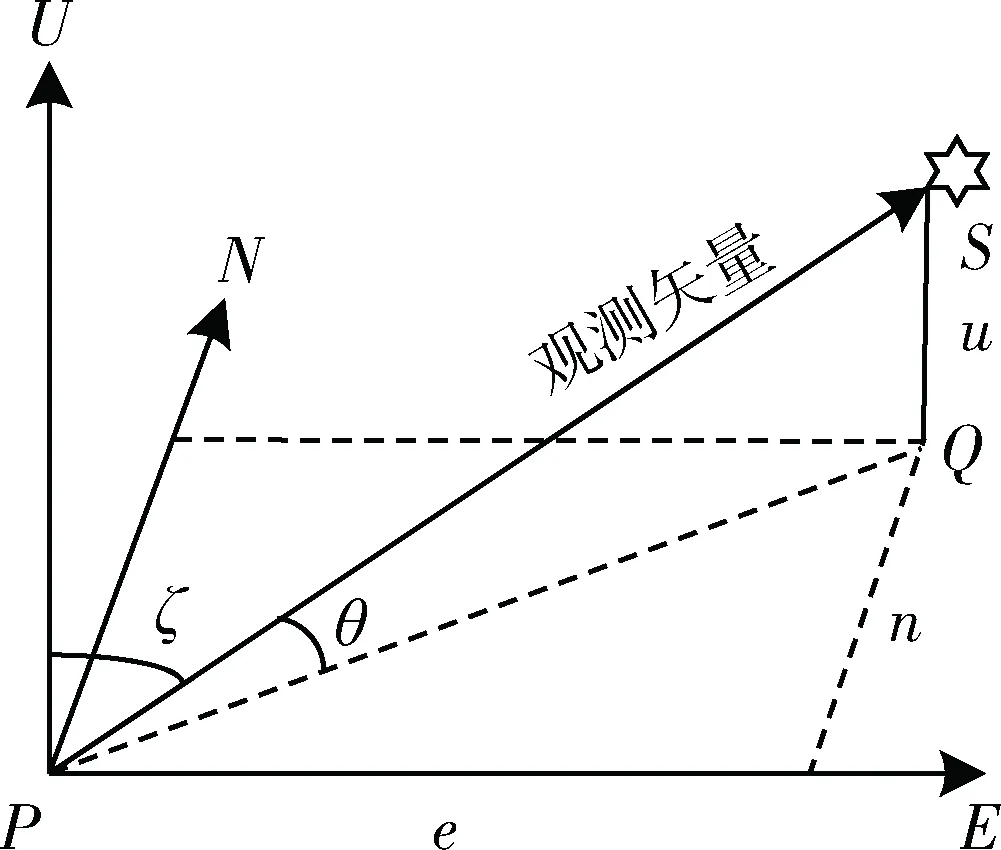
图1 仰角和方位角的定义

(1)

(2)

相对于接收机位置而言，如果1颗卫星的仰角小于0，则被认为是不可见星，其信号无法被接收。如果其仰角大于0但是过小，则其传递路径因离地面较近会受到过多干扰，因此多径效应会增大而可靠性变低。所以在可见星中需要将仰角过低的那些卫星排除掉，通常将门限设为10°。

在导航系统解算得到第一个定位结果后，根据卫星星历信息，可得出各卫星的仰角信息，进而便可优先在此刻可见星的范围内进行卫星的捕获。本文的选星算法在可见星的范围内首先剔除仰角小于上文所设门限值的卫星，在剩余满足条件的可见星中再做进一步的选择。

1.2 卫星信号的质量选择

上文考虑仰角信息对选星过程的影响，下面主要分析卫星信号质量在选星过程中的作用。仅用功率无法很好地衡量卫星的信号质量情况，这里采用信噪比表示，设P表示信号的功率，N表示噪声的功率，则信噪比的定义[9]可以表示如下：

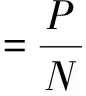
(3)

设Bn表示噪声的带宽，则载噪比C/N0与信噪比的关系如下:

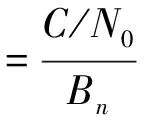
(4)

GPS接收机在某一时刻的可见星数量一般为4～11颗且一般大于4颗，由于复杂的环境影响及载体运动等内外部原因，卫星信号的质量会产生差异，下面对卫星信号质量对导航解算过程的影响进行分析。

采用定点定位的方式研究信噪比对接收机跟踪环路的影响，即设载体处于且一直处于静止状态，将全部的卫星通道带宽设为相同，则信噪比间的关系即为载噪比间的关系。设13号星的信噪比为0dB，图2所示为13号星的跟踪误差图。

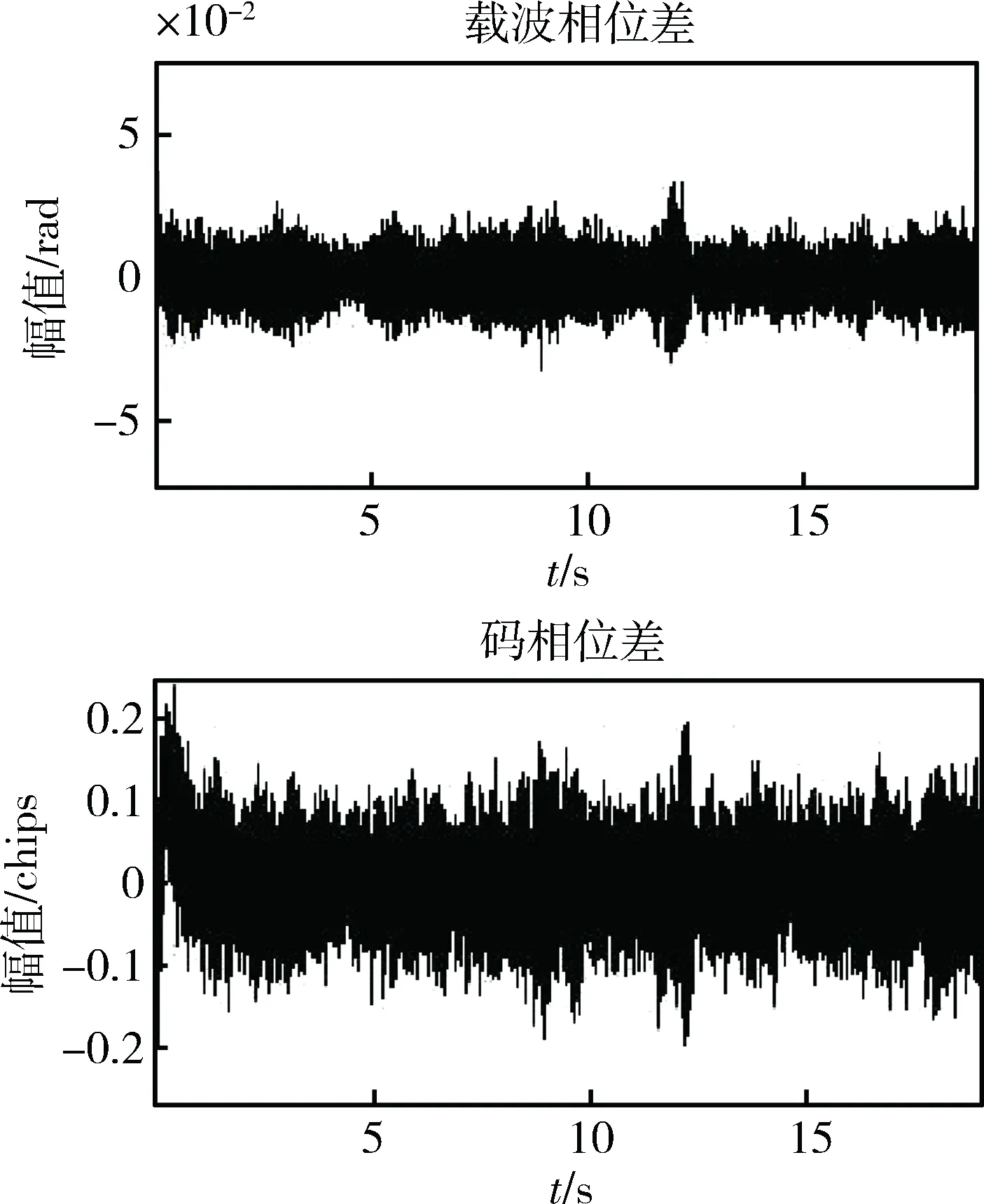
图2 13号星卫星通道跟踪误差

由图2可得其通道的跟踪误差非常小。设16号星的信噪比为-10dB，其跟踪误差图如图3所示。

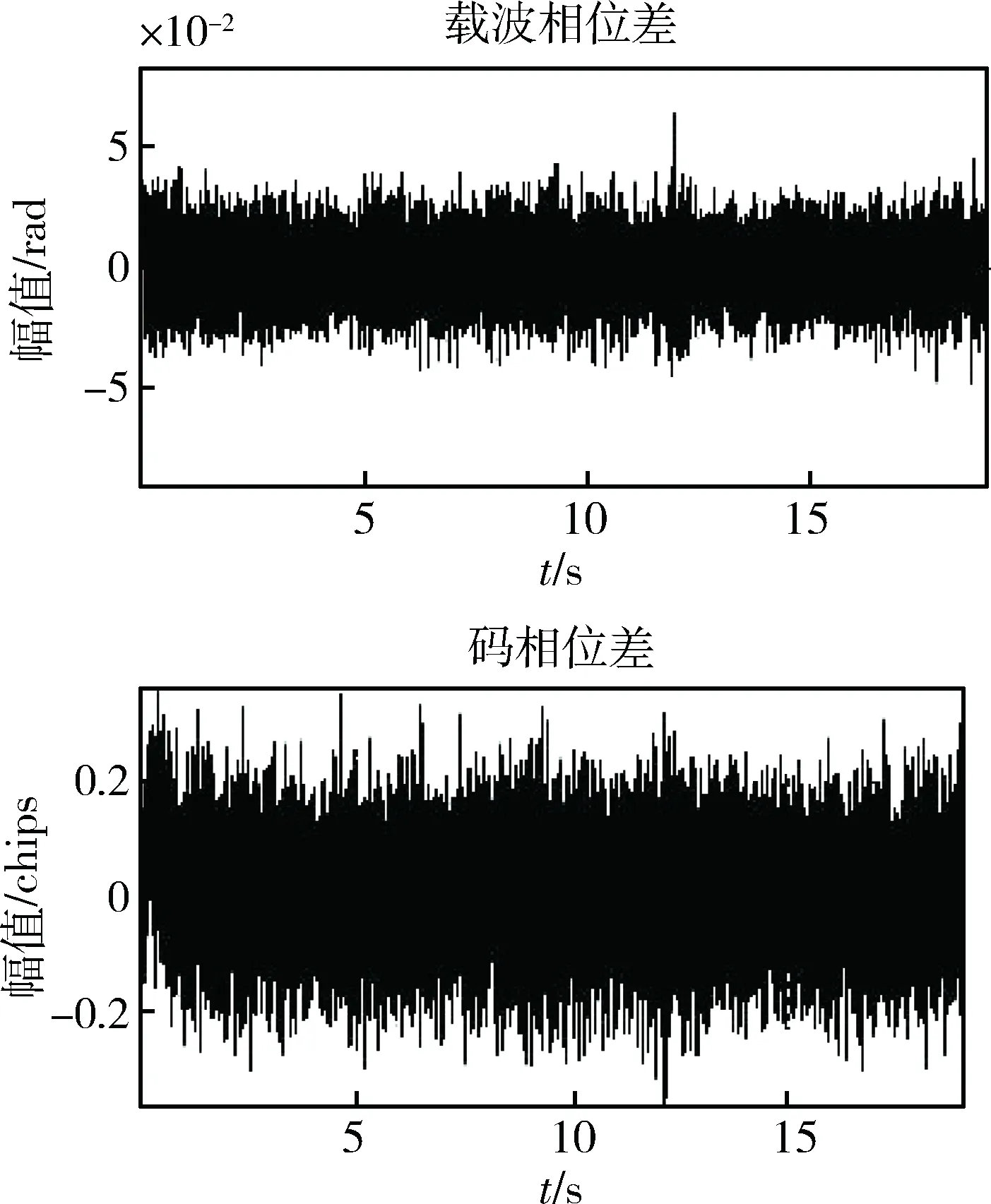
图3 16号星卫星通道跟踪误差

由图3可知，对于信噪比为-10dB的卫星信号，其通道的跟踪误差比13号星大，但仍可有效地实现卫星信号的跟踪。最后设定14号星的信噪比为-20dB，其对应的跟踪误差图如图4。

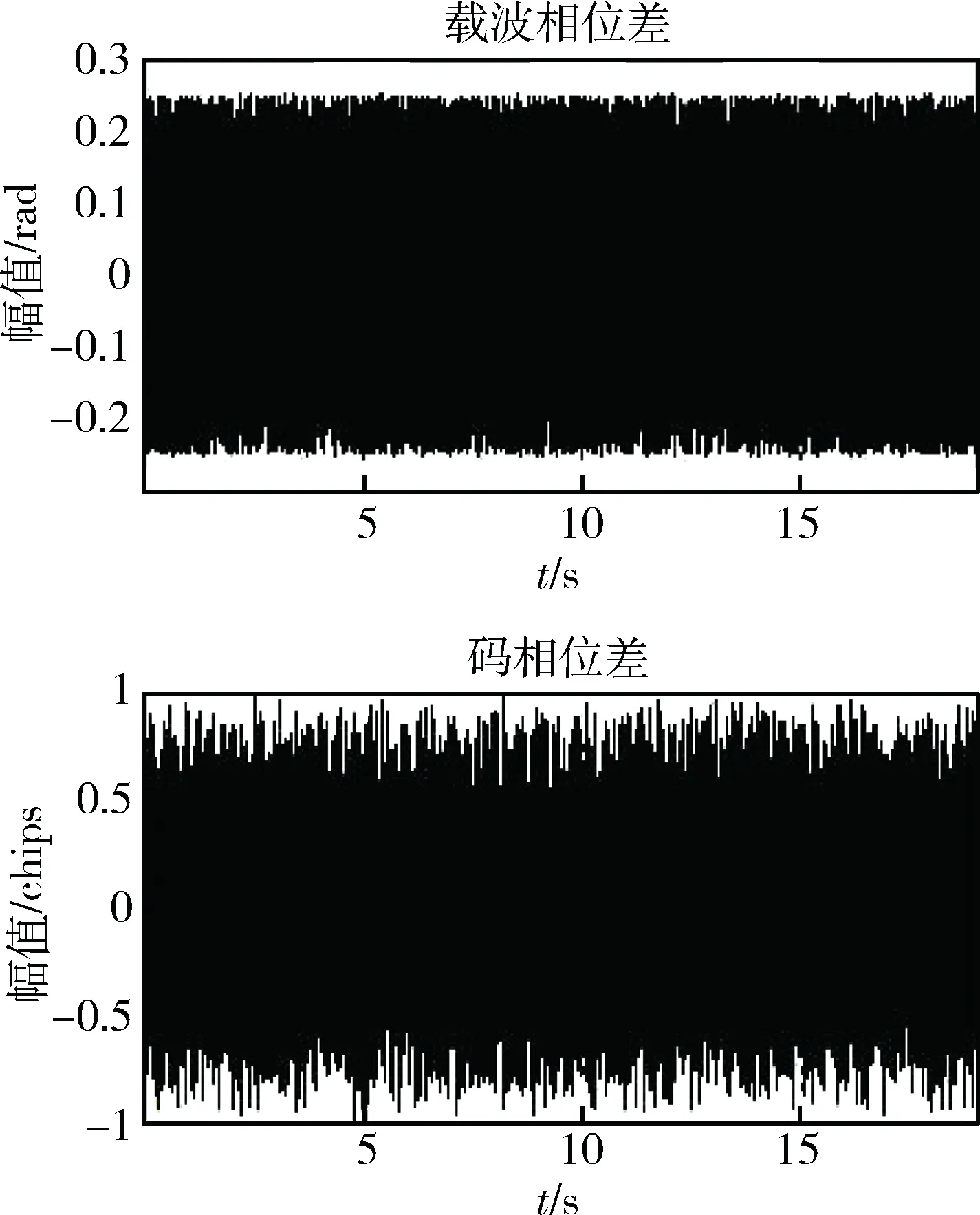
图4 14号星卫星通道跟踪误差

由图4可见，由于信噪比过小，信号相对过弱，14号星的跟踪误差过大，跟踪环路最终失锁。通过上文的实验对比，可以看出信噪比越小的卫星，其跟踪环路中对应的跟踪误差就越大，过小的信噪比无法有效跟踪相应的卫星信号。

由实验分析可知，卫星的信号质量对导航解算过程有较大影响，如果直接将信号质量差的卫星信号加入到解算过程，会影响定位结果的准确性。因此本文在保证用于解算的卫星数量不少于4颗的前提下，剔除信噪比较小的卫星信号。实验中，将卫星信号的信噪比门限值设为-16dB，即当某卫星的信噪比小于此值时，便可被认为是弱信号而放弃使用。

1.3 卫星的几何分布选择

上文主要讨论研究了仰角及信号质量对定位精度的影响，但选星过程还需要考虑另一个重要的影响因素，即几何精度因子。在导航系统定位过程中，一般估计载体位置和钟差的误差为：

(5)

(6)

(7)

(8)

设载体接收机的位置误差为σ：

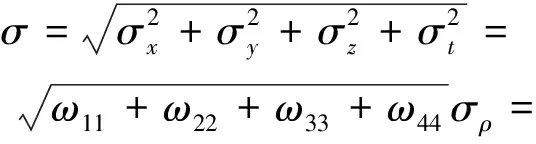
(9)

即可定义几何精度因子如下：

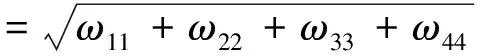
(10)

由几何精度因子的含义可知，其数值由卫星与接收机间的相对位置关系决定，卫星的几何分布代表了几何精度因子的数值大小。另外几何精度因子的值越小，表示测量误差被放大的倍数越小，因此为了保证定位的准确性，在选星过程中要选取对应几何精度因子值最小的卫星组合。传统的选星算法计算量过大，搜索速度慢，由于含有大量复杂的矩阵乘法和矩阵求逆运算，在计算机上实现起来相当占用资源。因此下面主要研究如何优化几何精度因子的选取过程，由选星数不同时的几何精度因子变化曲线[10]，可知理论上选星数量越多，几何精度因子的值越小，但其数值的减幅在选星数量增多的同时越来越小，尤其在数量大于6之后，该数值减幅不再明显。除了对定位精度的要求外，导航定位对运算速度也有比较高的要求，因此综合考虑定位精度、实时性，选星数目确定为6颗，此时定位精度较普遍使用的4星定位明显提高，且定位计算量增加也不大。

综合考虑，本文的选星过程总结如下：经过卫星的仰角及卫星信号质量的检测后，如果剩余的可见卫星数量大于6，则选取精度因子最小的6星卫星组合；否则，使用所有卫星通道的测量值。那么剩余的问题就在于如何在剩余可见星大于6颗时高效准确地选出最佳的6星组合。

本文提出了结合模糊算法的卫星组合选取策略，即在仰角大于10°的所有卫星中，选择仰角最大的作为第1颗，仰角第二大的作为第2颗,仰角最小的作为第3颗，将第3颗卫星的方位角分别增加90°、180°和270°，在这3个方位角附近的仰角与第3颗星的仰角最为接近的3个星就是第4、5和6颗星。为了综合方位角和仰角2个因素的影响，引入模糊数学的理念，找到两者之间必要的平衡，以取得更好的效果。

模糊综合评判过程一般分为以下过程：

1)首先确定影响事物的因素，在其基础上构造因素集

X=[x1x2…xn]

(11)

2)确定用于模糊综合评判的评语集

Y=[y1y2…ym]

(12)

3)确定因素集X中的每一元素xi对评语集Y中的每一元素yj的隶属度函数μij(i=1,2,…,n;j=1,2,…,m)。

4)用μij对因素集X中的每一元素xi做单元素评价，可得到模糊向量如下：

Zi=[μi1μi2…μim]

(13)

5)再用上面得到的单因素评价结果来构造用于表示这些因素间模糊关系的模糊矩阵如下：

(14)

7)做模糊变换如下：

Q=P·Z

(15)

其中，Q代表了被评判对象在评语集Y上的评判结果，其中的每个分量分别代表被评判对象对评语集Y中每一元素的隶属度。

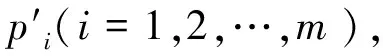
(16)

最后令

μ=P′·QT

(17)

便可计算得评判指标。

接下来在选择第4、5和6颗卫星时便借鉴了上文所列的模糊综合评判的思想。设已经选定的第3颗卫星也即剩余卫星中仰角最小的一颗方位角和仰角的大小分别为α和e，设除去已经选择的前3颗星外的其他可选择卫星的方位角和仰角分别为αi和ei，i=1,2,3,…,m。按上文所述，在选择最后的3颗卫星的过程中要考虑仰角和方位角2种因素的信息和影响。下面以α+90°与αi之间的夹角Ai和e与ei之间的夹角Ei作为衡量这2种因素的标准，则可构成模糊向量如下：

Z1=[A1A2…Am]

(18)

Z2=[E1E2…Em]

(19)

利用式(18)及(19)这2个模糊向量即可构造表示2个因素间模糊关系的矩阵如下：

(20)

接着需要确定各个因素的权重，并在其基础上构建权向量：

P=[p1p2]

(21)

p1+p2=1

(22)

最后完成模糊变换

Q=P·Z

(23)

Q中元素最小的一个对应的就是选择的第4颗卫星，同理，在选择完第4颗星后，围绕剩余的卫星，分别将上文过程中的α+90°替换为α+180°和α+270°进行计算，最后得到的最小元素所对应的卫星即为第5、6颗星。

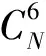
2 算法的仿真分析

根据前面的分析，以及设计的选星方案，进行仿真验证及具体的分析。首先是仰角门限的设定，根据经验当卫星仰角大于10°时，卫星信号受多径效应等干扰明显减弱，因此可以将其设为仰角门限值。本文处理的是仿真的GPS中频数据，中频频率为4MHz，设定信号的信噪比门限值为-16dB，当信噪比小于门限时该卫星信号即被认为是弱信号，相应的通道也被剔除。最后在余下的通道中选取6颗卫星，使其对应的几何精度因子最小，从而保证导航解算结果的准确性。

在本文所使用的卫星星历信息中，该时刻接收机能够接收到3、6、13、14、16、19、20、23、31号共9颗卫星的信号。其中14号星的信噪比为-20dB，其余卫星信号的信噪比均设为-10dB，因为PRN14的信噪比较低，因此该通道的观测值被剔除。图5给出了该时刻可见星的几何分布图，可以看出，20号卫星的仰角低于10°，因此也不使用该通道的观测量。如1.3中所述，接下来的工作即是在剩余的7颗卫星中选取拥有最小几何精度因子值的6星组合。

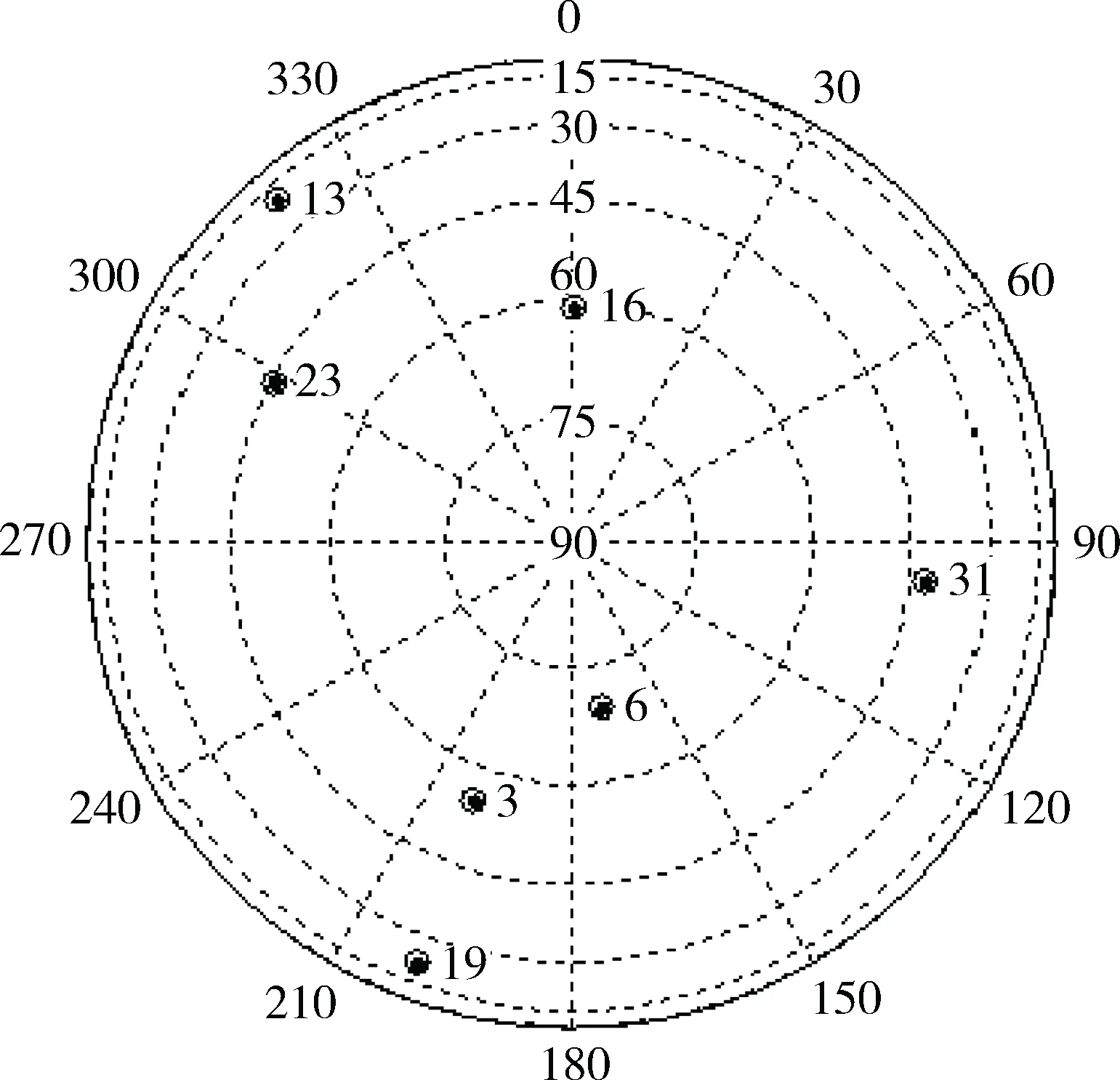
图5 可观测卫星几何分布图

首先使用模糊选星算法进行最佳卫星组合的选取，待选的7颗卫星的仰角及方位角信息如表1所示：

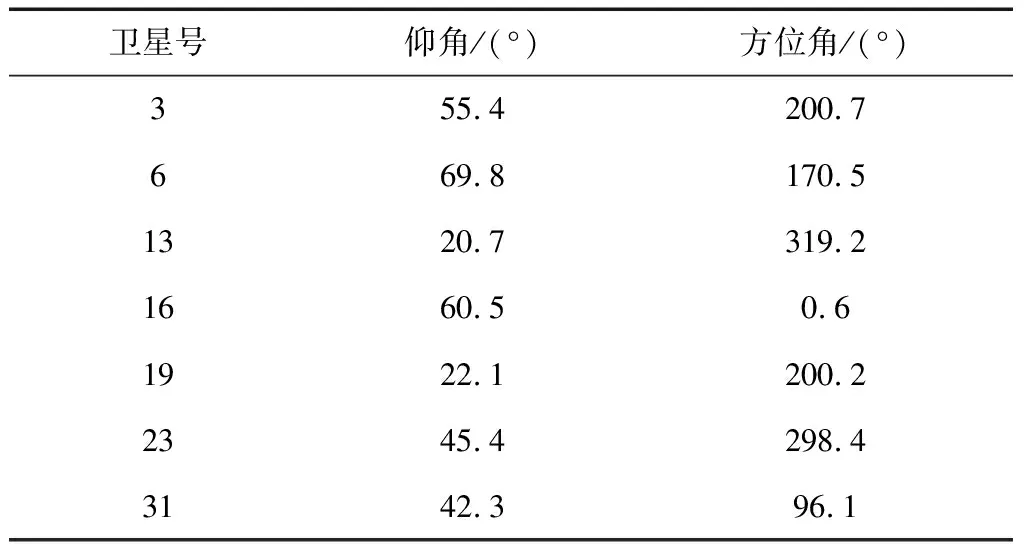
表1 待选卫星的仰角及方位角信息

结合上文的模糊选星算法过程，可得仰角最大的6号星为第1颗星，仰角第二大的16号星为所选的第2颗卫星，仰角最小的13号星即为所选的第3颗星，即13号星的方位角和仰角相当于算法中的α和e。继续按1.3中的步骤进行计算，本文中设P=[0.5 0.5]，依次得到第4颗星为31号星，第5颗星为19号星，第6颗星为3号星。因此模糊选星法在这里最终所选的最佳6星卫星组合为卫星3、6、13、16、19、31。

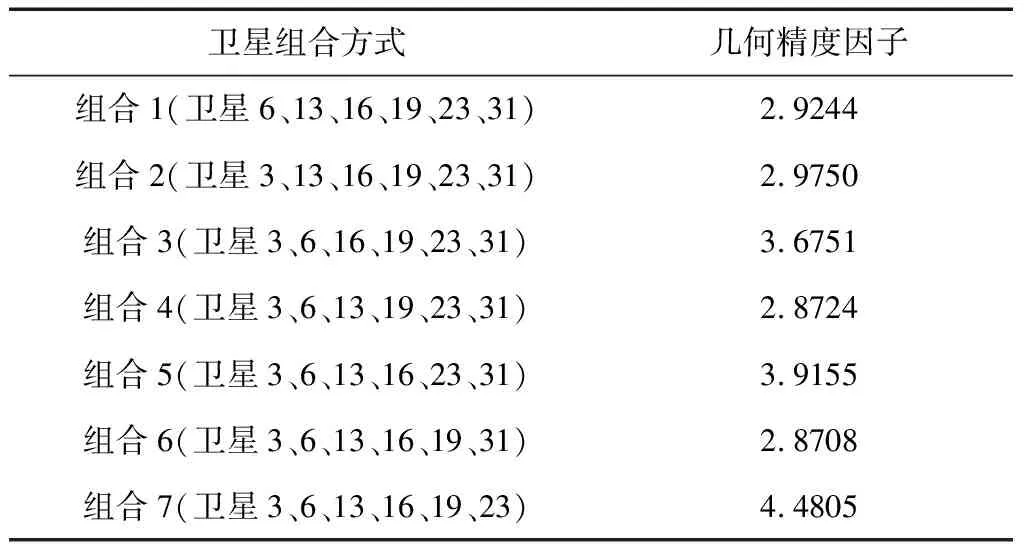
表2 可能的7种卫星组合方式的几何精度因子值

表中所示的卫星组合6(卫星3、6、13、16、19、31)的几何精度因子值最小，因此在最佳选星法中选用组合6。用其它2种快速选星方法得到了同样的结果，尽管相比最佳选星法大大减少了计算量，但仍旧需要对几何精度因子值进行计算。进而可知本文提出的模糊选星算法在仅需要简单的向量运算的情况下有着同最佳选星法相同的选取最佳卫星组合的能力。

为了进一步分析验证，设定一静止点，分别用上文的7种卫星组合进行中频数据的仿真，并用GPS接收机加以解算，表3显示并详细对比了各种组合方式的定位误差绝对值均值(m)及几何精度因子等值。

从表3可以看出文中分析的最佳卫星组合(组合6)的定位误差小于其他卫星组合情况，仿真结果表明，几何精度因子值越小的卫星组合能起到增强定位准确性的效果。也证明了经过卫星仰角和信号质量检测排除后，用模糊选星算法能够选出使定位误差最小的最佳卫星组合。

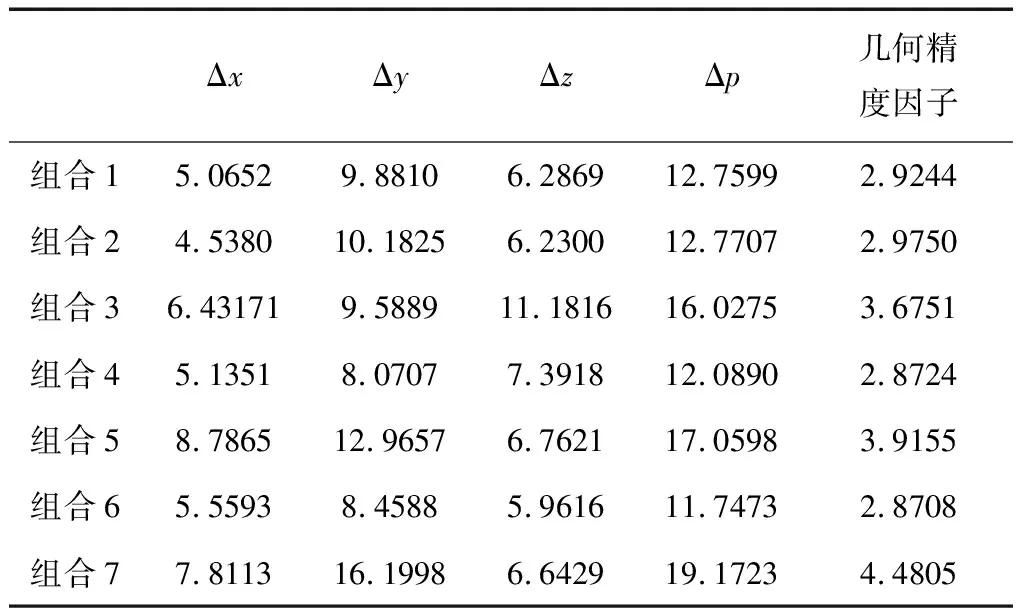
表3 各卫星组合定位误差对比

3 结论

研究了导航定位过程中的卫星选取过程，传统的最佳卫星组合选取方法运算过于复杂，改进的选星方法在计算量上做了优化，但仍需求解几何精度因子，同时卫星的仰角和信号质量也对定位结果有较大影响。对此本文提出了首先剔除低于仰角及信号质量门限值的卫星，再以模糊综合评判的方式综合考虑剩余待选卫星仰角及方位角，最终选出最佳卫星组合的一系列选星策略。策略在保证精度的同时只需要简单的向量计算。最后通过仿真实验及其相关的数据分析证明了算法的有效性。

参 考 文 献

[1] Bo Wang, Shunting Wang. An Improved Satellite Selection Method in Attitude Determination Using Global Positioning System (GPS)[J]. Recent Patents on Space Technology, 2009(1): 6-11.

[2] M.R. Mosavi. Applying Genetic Algorithm to Fast and Precise Selection of GPS Satellites[J]. Asian Journal of Applied Sciences , 2011,4(3):229-237.

[3] Miaomiao Wei, Ju Wang. An Improved Satellite Selection Algorithm[C]. Signal Processing (ICSP):IEEE, 2012:2258-2261.

[4] Miaomiao Wei, Ju Wang. A New Satellite Selection Algorithm for Real-time Application[C]. International Conference on Systems and Informatics, 2012:2567-2570.

[5] Miaoyan Zhang, Jun Zhang. A Fast Satellite Selection Algorithm: Beyond Four Satellites[J]. IEEE Journal of Selected Topics in Signal Processing, 2009, 3 (5):740-747.

[6] 杨蓝，王祖林，尚佳栋等．卫星导航系统基四选星算法[J]．电光与控制,2015,22(7):61-65．

[7] 田安红，付承彪，孔德剑．一种新的基于加权行列式的选星算法 [J]．弹箭与制导学报，2014，34(4):155-157．

[8] 吴瑞祥，蔡体菁. 基于高度角和方位角的选星方法[J]. 船舶电子工程，2009,29(11)：73-75.

[9] 谢钢．GPS原理与接收机应用 [M]．北京：电子工业出版社，2009.

[10] 丛丽，谈展中. 提高卫星导航定位精度和实时性的选星算法 [J]. 系统工程与电子技术，2008,30(10):1914-1917.(Cong Li, Tan Zhanzhong. Satellite Selection Algorithm to Improve Precision and Real-time Performance of GPS Positioning[J]. Systems Engineering and Electronics; 2008,30(10):1914-1917.)

[11] 彭思博，郭承军，刘赋山. 北斗/GPS双模定位中快速选星算法研究 [J]. 全球定位系统，2017,42(3):11-14.

[12] 马宏阳，程鹏飞，李冉，黄华东. 一种多系统组合导航快速选星方法 [J]. 测绘工程，2016,25(1):59-64.