欠驱动VTOL飞行器非线性信息融合控制
赵 宾 高春雷 胡 洲
1.南京航空航天大学金城学院,南京 211156 2. 南京航空航天大学自动化学院,南京 211106 3. 四川航天系统工程研究所,成都 610100
垂直起降 ( vertical take-off and landing,VTOL) 飞行器具有优良的短距、垂直起降性能,在未来战争中将发挥极其重要的作用,目前已经成为世界各国争相研究的对象。悬停模式下的VTOL飞行器具有2个控制输入和3个运动自由度,是一个典型的欠驱动系统[1]。
VTOL等飞行器的欠驱动特性和强非线性耦合特性,使其控制问题变得较为复杂,引起了诸多控制专家的兴趣。文献[2]针对VTOL飞行器的强输入耦合问题,采用光滑静态状态反馈实现了其全局配置稳定。文献[3]利用标准的Lyapunov方法,提出了一种新的非线性反馈控制律,补偿VTOL的建模误差并提高其抗干扰鲁棒性能,实现了飞行器对给定参考轨迹的稳定跟踪。文献[4]针对带输入限制的VTOL飞行器轨迹渐近跟踪问题,设计了一种基于光滑函数的简单控制器。文献[5]针对带有界外部扰动的VTOL无人飞行器提出了一种自适应位置跟踪算法。文献[6]基于高增益观测器提出了一种滑模控制策略,可以使VTOL飞行器在轨迹跟踪过程中呈现指数稳定的性能。文献[7]研究了带2个力矩的欠驱动航天器的三轴姿态稳定问题,提出一种3层滑模控制方案,能全局渐近地镇定欠驱动系统。文献[8]提出一种位置反馈动态面控制算法,减轻计算负担,实现非最小相位欠驱动VTOL飞行器位置准确跟踪。文献[9]为解决严重耦合的VTOL欠驱动系统的输出跟踪问题,将动力学模型解耦成一个最小相位系统和一个非最小相位系统,分别设计滑模控制器,实现了对轨迹的无稳态误差跟踪。文献[10]针对零角动量欠驱动航天器姿态控制问题,设计逆最优反馈控制律,可使姿态运动渐近稳定至所需平衡点。文献[11]设计了一种新型的VTOL,设计其姿态控制系统,通过双闭环PID控制器实现飞行器的姿态稳定。
文献[2-11]均分别从不同角度运用不同方法对VTOL等欠驱动飞行器的控制问题进行了研究。本文将在非线性信息融合理论[12]的基础上,提出一种VTOL飞行器非线性信息融合控制方法,以解决其跟踪控制问题。相比文献[2-11]中所用方法,该方法可以避免求解非线性最优控制问题中非线性黎卡提方程,而且基于被控对象的离散模型设计,有易于实现的特点,具有较好的快速稳态跟踪性能。
1 欠驱动VTOL飞行器动力学系统建模
鹞式喷气战机是世界上第一种实用型垂直/短距起落飞机,由一台带4个排气喷嘴的涡轮风扇发动为其提供动力,是一种典型的VTOL飞行器[13]。这种飞行器有2种工作模式以及这2种模式间的过渡模式。模式1:翼承载前飞模式,如固定翼喷气式飞机一样;模式2:喷气承载机动模式(空中悬停),由排气喷嘴为飞机提供垂向推力,通过反应控制阀为飞机提供滚转力矩。模式2无法直接实现横向运动,需要依赖滚转姿态控制完成,是这类飞行器的固有限制,体现了欠驱动特性,这也是我们对VTOL悬停控制感兴趣的原因。
如图1所示为VTOL飞行器的悬停示意图,拥有最小的状态变量和输入量个数,但仍然保留了为一个实际的VTOL飞行器设计控制律时所必需考虑的特征。据文献[13],VTOL的动力学模型可表示为如式(1)所示:
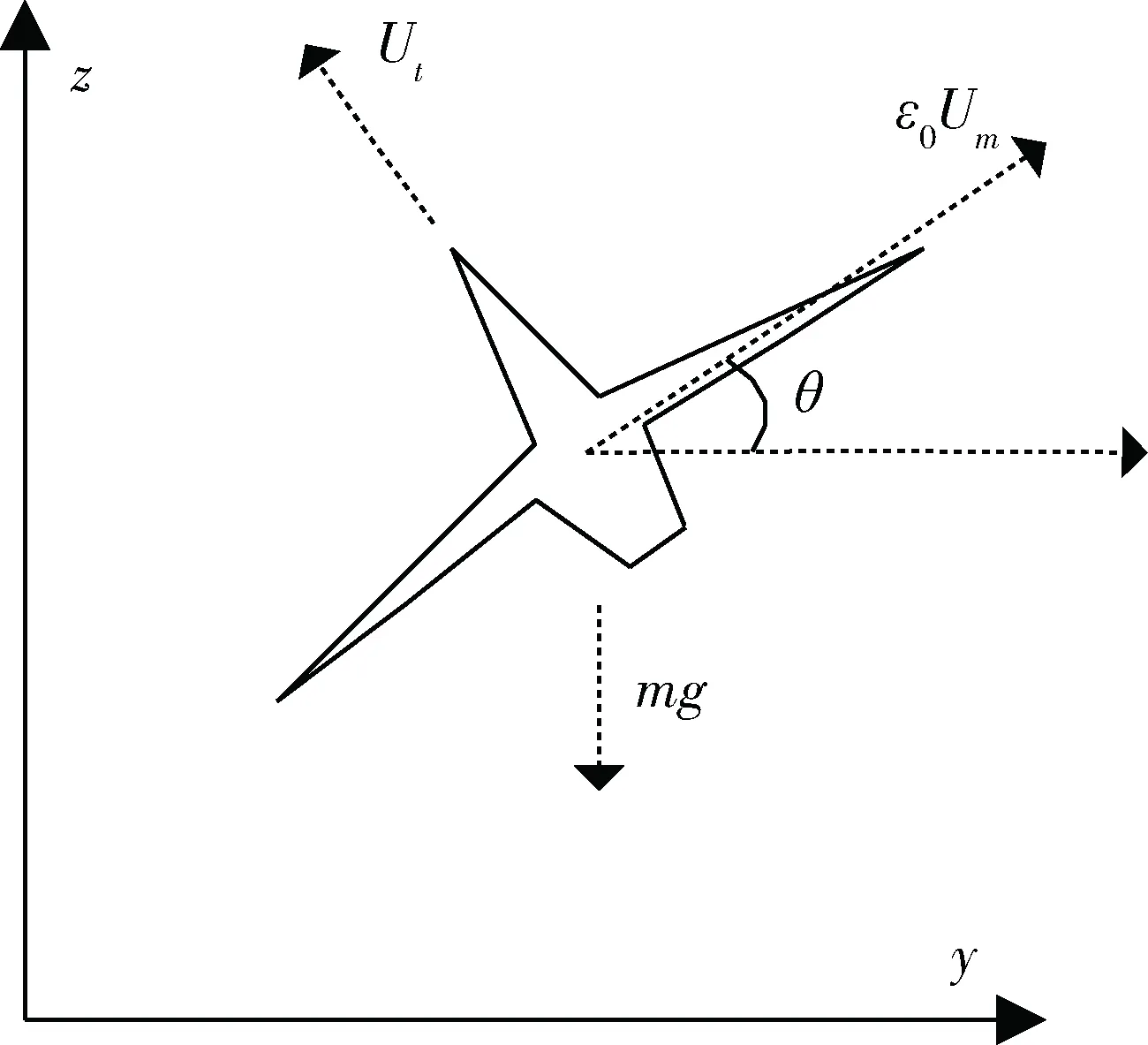
图1 VTOL飞行器悬停示意图
(1)
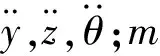

(2)
式中,将第2个和第4个微分方程写成矩阵形式,可得:
(3)
由式(3),若ε0≠0,无论x5取何值,必然存在如下可逆非线性变换:
(4)
用式(4)中新的输入变量v1和v2代替原始输入变量Ut和Um,实现对状态变量x2和x4的解耦:
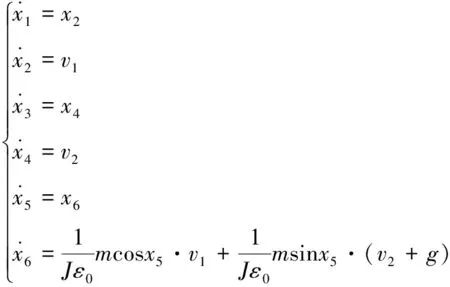
(5)
式(5)可表示为如下统一状态模型:

(6)
其中,x=[x1,x2,x3,x4,x5,x6]T,v=[v1,v2]T。信息融合控制算法是基于被控系统的离散模型设计的,所以需要将式(6)进行离散化,采用如式(7)所示的泰勒级数法[14]对上式进行非线性离散化。
(7)
S[i](x(k),v(k))可通过递归表达式(8)和(9)来求解:
S[i](x(k),v(k))=f(x,v)|tk,i=1
(8)
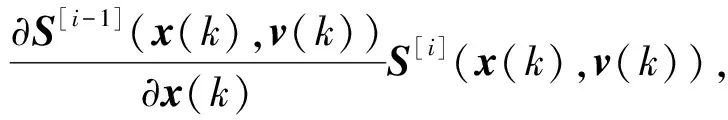
(9)
一般情况下,如果采样时间T≤0.1s,则式(7)中一阶项为主要部分,二阶及二阶以上的项可以忽略。如果T取值较大,为了模型更精确,则需保留式(7)中二阶项或更高阶项。本文中,取T=0.02s,对式(5)采用如式(7)所示的方法离散化,并取一阶项,可得离散化后的状态方程为:
x(k+1)=f(x(k),v(k))
(10)
其中,k=1,…,n代表时间序列,

本文所讨论的内容只关心VTOL飞行器的垂向位置、横向位置和滚转角,所以系统输出方程可以构造如下:

(11)
2 非线性信息融合控制算法
2.1 非线性信息融合控制问题描述
考虑如下非线性离散控制系统:
x(k+1)=f(x(k),u(k))
(12)
y(k)=h(x(k))
(13)
其中,x(k)∈Rn是状态向量,u(k)∈Rm是控制向量,y(k)∈Rp是输出向量,f(·,·)是Rn×Rm上的n维光滑向量场,h(·)是Rp上的p维光滑单调向量场,x(0)=x0是状态向量的初始值。
对于信息融合最优跟踪控制问题,可建立如式(14)所示的控制性能指标,即求出一组控制序列u(k),使该式达到极小值[12]:
(14)
其中,y*(k)是期望跟踪轨迹,上式第1项表示在控制过程中,各维实际输出都必须跟踪期望输出,使得跟踪误差最小,Q(k)表示对各维输出跟踪误差的约束要求,可以看作是跟踪误差的信息量;第2项表示在控制过程中,对各维控制量的能量要求,在输出量满足指标要求的前提下,要求控制能量最小,R(k)表示对各维控制量的能量约束要求,可看作控制能量的信息量。R(k)和Q(k)均为正定对称矩阵。
2.2 非线性信息融合控制算法的设计
定理1[12]若关于x的各种信息表示为:
(15)


(16)
(17)
在定理1的基础上,针对VTOL飞行器在悬停模型下的控制问题,分析其信息融合的具体信息和任务,设计推导VTOL非线性信息融合递推算法。
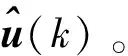
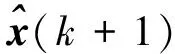
x(k+1)=f(x(k),u(k))
(18)
0=u(k)+n(k)
(19)

(20)
其中,w(k+1)是均值为0、方差为P-1(k+1)的白噪声。将式(18)代入式(20),运用定理1对所有关于u(k)信息进行融合,可得:
(21)

x(k+1)=f(x(k),u(k))
(22)

(23)
y*(k)=h(x(k))+m(k)
(24)
0=u(k)+n(k)
(25)
将式 (23)、(25)代入 (22),可得到:
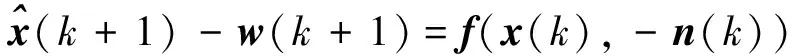
(26)
方程(26)可变换为:

(27)
其中,v(k)是均值为0、方差为M-1(k)的白噪声。
M(k)=(P-1(k+1)+B(k)R-1(k)BT(k))-1
(28)
运用定理1,融合式(24)、(27)中关于x(k)的信息,可以得到:
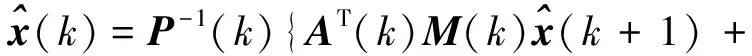
(29)
P(k)=AT(k)M(k)A(k)+HT(k)Q(k)H(k)
(30)
2.3 非线性信息融合控制算法流程
2)设置控制步数k=0;
3)设置迭代序号i=1;
4)计算如下偏导数;
其中,p=k~(k+kf-1),kf为预见步数。
5)计算协状态及其信息量,设置初始迭代值;

其中,Kf=k+kf-1,计算
M(i)(p)=
[P(i)-1(p+1)+B(i)(p)R(i)-1(p)B(i)T(p)]-1
(31)
P(i)(p)=A(i)T(p)M(i)(p)A(i)(p)+
H(i)T(p)Q(p)H(i)(p)
(32)

(33)
6)计算

为了提高计算的实时性,第5步中式(31)~(33)的逆向迭代计算过程可以离线进行,将大大减小在线计算量。
3 仿真验证与分析
本节将通过仿真验证非线性信息融合控制算法的有效性。取采样时间T=0.02s,预测步数kf=50。飞行器质量m=5×104kg,转动惯量J=2×105kg·m2。
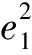


图2 控制量Ut曲线图

图3 控制量Um曲线图
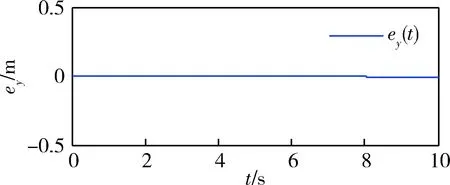
图4 横向位置跟踪误差曲线

图5 垂向位置跟踪误差曲线

图6 滚转角跟踪误差曲线
从图2~3可以看出控制量响应迅速、稳定收敛。从图4~6可以看出,在VTOL飞行器起飞过程中,本文所提出的信息融合控制算法能实现对垂向期望轨迹的快速、准确跟踪,并同时保持横向位置和滚转角镇定。相比于文献[8-9]中的控制方法,本方法求解过程简单,易于实现,均实现了VTOL飞行器的稳态跟踪控制,且本方法在2s内即达到稳态跟踪,具有较好的快速跟踪性能。仿真结果表明,该算法对横向运动和垂直运动具有良好的解耦性能,能够实现VTOL飞行器的快速稳态跟踪。
4 结论
针对VTOL飞行器在悬停模型下的控制问题,提出了一种非线性信息融合控制方法。仿真结果表明,该算法具有良好的控制效果和解耦性能。该算法避免了非线性最优控制问题中非线性黎卡提方程的求解,且完全基于被控对象的离散状态模型设计,而现在实际工程中大多是依赖计算机的数字控制系统,所以本算法具有较强的实用性。
参 考 文 献
[1] Olfati-Saber R. Nonlinear Control of Underactuated Mechanical Systems with Application to Robotics and Aerospace Vehicles[D]. Massachusetts Institute of Technology, 2000:157-160.
[2] Olfati-Saber R. Global Configuration Stabilization for the VTOL Aircraft with Strong Input Coupling[J]. Automatic Control, IEEE Transactions, 2002, 47(11): 1949-1952.
[3] Hua M D, Hamel T, Morin P, et al. A Control Approach for Thrust-propelled Underactuated Vehicles and Its Application to VTOL Drones[J]. Automatic Control, IEEE Transactions, 2009, 54(8): 1837-1853.
[4] Ailon A. Simple Tracking Controllers for Autonomous VTOL Aircraft with Bounded Inputs[J]. Automatic Control, IEEE Transactions, 2010, 55(3): 737-743.
[5] Roberts A, Tayebi A. Adaptive Position Tracking of VTOL UAVs[J]. Robotics, IEEE Transactions on, 2011, 27(1): 129-142.
[6] Gong H S, Liu J K. Sliding Mode Control for VTOL Aircraft Based on High-Gain Observer[C]// Instrumentation, Measurement, Computer, Communication and Control (IMCCC), 2012 Second International Conference on. IEEE,2012: 305-309.
[7] 王冬霞, 贾英宏, 金磊等. 欠驱动航天器姿态稳定的分层滑模控制器设计[J]. 宇航学报, 2013, 34(1): 17-24. (Wang Dongxia, Jia Yinghong, Jin Lei, et al. Hierarchical Sliding-mode Control for Attitude Stabilization of an Underactuated Spacecraft[J]. Journal of Astronautics, 2013, 34(1): 17-24.)
[8] 袁瑞侠, 刘金琨. 欠驱动VTOL飞行器的位置反馈动态面控制[J]. 系统工程与电子技术, 2014, 36(11): 2266-2271. (Yuan Ruixia, Liu Jinkun. Position Feedback Dynamic Surface Control for Underactuated VTOL Aircraft[J]. Systems Engineering and Electronics, 2014, 36(11): 2266-2271.)
[9] 王元超, 孙辉. 基于VTOL飞行器的滑模控制器设计[J]. 计算机测量与控制, 2016, 24(6): 102-105. (Wang Yuanchao, Sun Hui. Sliding Mode Controller Design for VTOL Aircraft[J]. Computer Measurement & control, 2016, 24(6): 102-105.)
[10] 宋道喆, 耿云海, 易涛. 零角动量欠驱动航天器逆最优稳定控制律设计[J]. 宇航学报, 2016, 37(6): 729-736. (Song Daozhe, Geng Yunhai, Yi Tao. Inverse Optimal Stabilization of an Underactuated Spacecraft in a Zero Angular Momentum Mode[J]. Journal of Astronautics, 2016, 37(6): 729-736.)
[11] 陈胜, 华荣, 冀宝霖. 双涵道倾转垂直起降飞行器模型与系统研究[J]. 航天控制, 2017, 35(1): 31-36. (Chen Sheng, Hua Rong, Ji Baolin. Double Tilting Ducted Aircraft Model and System Design[J]. Aerospace Control, 2017, 35(1): 31-36.)
[12] Wang Z S, Wang D B, Zhen Z Y. Primary Exploration of Nonlinear Information Fusion Control Theory[J]. Science in China Series F: Information Sciences, 2007,50(5): 686-696.
[13] Lin F, Zhang W, Brandt R D. Robust Hovering Control of a PVTOL Aircraft[J]. Control Systems Technology, IEEE Transactions on, 1999, 7(3): 343-351.
[14] Zhang Z, Un An D, Kim H, et al. Comparative Study of Matrix Exponential and Taylor Series Discretization Methods for Nonlinear ODEs[J]. Simulation Modelling Practice and Theory, 2009, 17(2): 471-484.
[15] 王志胜, 姜斌, 甄子洋. 融合估计与融合控制[M]. 北京: 科学出版社, 2009:233-236. (Wang Z S, Jiang B, Zhen Z Y. Fusion Estimation and Fusion Control[M]. Beijing: Science Press, 2009:233-236.)

