颤振主动抑制的LPV控制设计

郑晓珂, 唐 炜， 王立博， 王 波

(西北工业大学自动化学院， 陕西 西安 710129)

引 言

颤振是气动力、弹性力和惯性力的耦合作用而发生的一种自激振动，是气动弹性系统动力学失稳的一种表现形式，会导致飞行器结构短时间内破坏，酿成灾难性后果。现代飞行器设计由于采用了轻柔结构，并且追求高速、高机动性，颤振问题显得愈加突出。因此，如何进行有效的颤振主动抑制是飞行器设计必须解决的关键问题。

现代控制理论早已应用于颤振抑制。LQR控制[1]和LQG控制[2]是早期研究的主流方法。近年来，鲁棒控制因其能够描述对象的不确定性，已成为颤振抑制的一种有效设计方法。在文献[3]中，H∞和μ综合控制被用于BACT风洞模型的颤振抑制，取得了较好的鲁棒性和抗干扰性。

飞行器因其飞行状态变化形成了快速时变的特点，鲁棒控制只是提高了控制律的适用范围，并不能解决根本控制律的大范围宽自适应性问题。最近，线性变参数方法(LPV)因其能反映系统参数的时变特性而被广泛关注。作为一种增益调参方法，LPV控制既能兼顾全局鲁棒性又能表现出参数自适应性。例如：文献[4]针对BACT机翼模型设计了以动压和马赫数为调度参数的LPV增益调度控制器进行颤振抑制，仿真结果表明效果良好。文献[5]则针对BFF vehicle设计H∞和LPV控制器，并比较了二者的性能。LPV控制技术目前已被用于试验验证机X-56A的颤振抑制研究中[6]。

本文旨在探索适用于颤振抑制的LPV控制器设计方法，结合LPV斜投影法和Lyapunov函数方法给出了一种包括模型降阶在内的LPV控制器快速实现方法，并将其应用于Goland Wing机翼的颤振抑制。仿真结果表明该控制器能够胜任在较宽飞行包线范围内的颤振抑制。

1 线性变参数模型

LPV模型是一种时变的状态空间模型，其定义如下

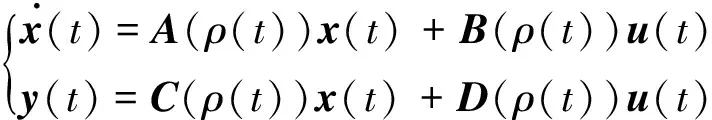
(1)

式中ρ(t)为实时可测的调度参数。矩阵A,B,C,D是ρ(t)的已知函数，对于飞行器而言，ρ可以是飞行高度、速度、动压等变化参数。

目前，LPV模型的表示方法主要包括线性分式变换(LFT)法[7]；网格线性化法[8]和状态矩阵的多胞形法[9](仿射参数依赖形)。本文将采用网格法表示LPV模型。建立气弹系统的LPV模型是开展LPV控制的基础。现有LPV建模包含了理论建模和实验建模。前者借助气动流体计算和有限元结构分析，得到一个阶次高达数百阶，乃至上千阶的LPV模型，这显然无法满足LPV控制对模型阶次的要求，因此对理论模型降阶必不可少。后者通常采用全局或局部辨识方法[10-11]，是理论模型修正的辅助手段。本文将主要研究基于理论模型的LPV控制。

2 LPV斜投影降阶

高保真的飞行器气弹模型不仅含有刚体运动模型，还含有弹性模态动态特性，原始模型阶次很高，为了得到面向控制的LPV模型，需对高阶模型进行降阶处理。LPV模型降阶不同于LTI模型，其降阶过程需要考虑多个离散网格点的状态空间一致问题，同时，计算量也是困扰模型降阶的主要难点。本节采用的LPV斜投影降阶法[12]适用于稳定的LPV系统，能有效解决以上两个问题。

LPV降阶模型定义如下

(2)

式中Ared,Bred,Cred,Dred的阶次应控制在20阶以下。

2.1 LPV模型平衡变换

类似于LTI模型的平衡截断法，LPV模型可通过计算广义可控Gramian矩阵Xc,ρ和广义可观Gramian矩阵Xo,ρ进行LPV模型的平衡，广义可控可观矩阵满足下列LMIs

(3)

(4)

进而得到LPV系统的平衡变换：

(5)

(6)

2.2 基于变参数斜投影的平衡截断

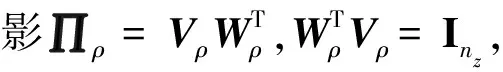
(7)

(8)

系统(8)即为希望得到的降阶模型。

2.3 算法实现

(1)局部LTI模型：计算每个网格点ρk⊂{ρ1,…,ρm}处模型的Cholesky分解和奇异值分解(SVD):

(9)

(10)

(2)全局LPV模型：由SVD近似计算变参数主子空间span(Lc,ρU1,ρ)

(11)

变参数斜投影平衡截断为

(12)

综上可知，LPV斜投影降阶法是用变参数的核定义了投影的方向，用常量矩阵V保证降阶LPV系统的状态一致性，同时避免了参数率的引入。

3 LPV控制设计

假设广义对象有如下形式

(13)

其中为了简化推导过程，式中假设D11(ρ)=0, D22(ρ)=0，同时，D12(ρ)，D21(ρ)被转化为标准形式。

因此，从y到u的反馈线性变参数控制器可定义为

(14)

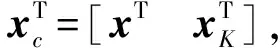
(15)

其中

(16)

(17)

(18)

(19)

LPV控制器的求解由如下定理给出。

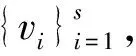
(20)

(21)

(22)

如果这些条件满足，定义

(23)

(24)

(25)

进而，可得到n维的反馈控制器，定义如下：

Q-1(ρ)X(ρ)L(ρ)C2(ρ) -

(26)

BK(ρ): = -Q-1(ρ)X(ρ)L(ρ)

(27)

CK(ρ): = F(ρ)

(28)

DK(ρ):=0

(29)

其中：

(30)

由式(20)～(22)可知：LPV控制器的可解条件是无穷维的LMI优化问题。为了简化问题，可以通过一组基函数定义矩阵变量

(31)

4 应用算例

本文以Goland Wing机翼模型验证LPV降阶和控制算法的有效性。Goland Wing是一副小展弦比的矩形机翼，其几何外形和片条的划分如图 1所示[14]。选择机翼的前4阶模态建模，机翼均匀分布12块片条，每块片条入流项个数为7个，系统输出为机翼的模态坐标，1个控制舵面输入。利用片条理论和有限元计算，可得到一个92阶、以来流速度V为变量的初始状态空间模型。

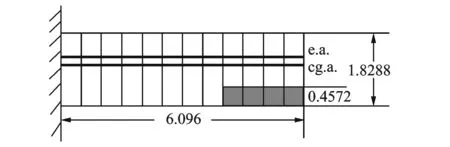
图1 Goland Wing片条划分(单位:m)Fig.1 Goland Wing and strip division (Unit: m)

4.1 降阶效果

根据系统的Hankel奇异值，初步选择降阶后的系统状态矩阵为12阶。利用本文研究的LPV斜投影降阶方法只需2 s即可完成模型降阶。为了说明模型的有效性，图2对比了全阶系统和降阶系统在稳定状态点V=[102∶2∶132] m/s的Bode图，由图可知，在频率低于104rad/s时的Bode图与原始系统基本重合，较好保留了系统的频率特性。

图2 全阶和降阶模型的Bode图对比Fig.2 Bode of full-order versus reduced-order model

图3比较了全阶系统和降阶系统在整个变参数空间的极点移动情况，浅色到深色的渐变过程为速度由低到高的过程。由图3可以看出，降阶模型与全阶模型的轻阻尼模态轨迹基本重合，而轻阻尼模态是诱发颤振的主要模态。

图3 飞行包线内的极点移动图Fig.3 Pole migration across flight envelope

LPV系统是时变的，针对单点的LTI模型分析并不能抓住LPV模型的时变本质，因此，有必要针对参数轨迹开展时域仿真。图4所示为选取的参数轨迹，该轨迹包含了具有高变化速率的完整来流速度参数空间，同时，比较了全阶和降阶系统沿着时变参数轨迹的阶跃响应，可以看出降阶模型很好地与全阶模型重合，保留了系统的时变特性，其他输入输出与此类似。

图4 LPV仿真Fig.4 LPV simulation

4.2 LPV控制效果

针对降阶后的12阶机翼模型，由频率特性得到随着速度的增加一阶模态频率和二阶模态频率相互接近。求得颤振临界速度为136.205 m/s，颤振频率为11.1408 Hz。

控制框图如图5所示，其中，Wperf为性能权重函数；Wu为输入加权函数；Wnoise为测量噪声权重；Wdist为扰动权重函数，以上各权重函数取值如下：

Wperf=2diag(0.015,0.015,0.05,0.05)

Wu=(12/π)I1×1

Wn oise=0.001I4×4；Wdist=I1×1

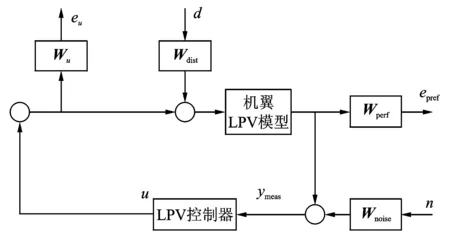
图5 控制设计框图Fig.5 Control Design block diagram

通过将权重函数取为常量值，可得到较为低阶的控制器。

由图6可以看出在设计的包线范围V=[126:2:156] m/s内，控制器的振动抑制效果十分明显。图7为时域仿真，分别为V=136.205 m/s和V=150 m/s时输入到输出1的阶跃响应，由图可以看出当系统发生等幅或者发散振动时，LPV控制器能够快速有效地抑制振动，使系统处于稳定状态。

由图6可以看出在设计的包线范围V=[126:2:156] m/s内，控制器的振动抑制效果十分明显。图7为时域仿真，分别为V=136.205 m/s和V=150 m/s时输入到输出1的阶跃响应，由图可以看出当系统发生等幅或者发散振动时，LPV控制器能够快速有效地抑制振动，使系统处于稳定状态。

同时，在每个状态点设计H∞控制器与LPV控制的对应状态点的控制器进行比较，图8为颤振速度V=136.205 m/s的对比图。由图可以看出，LPV控制器能够取得与H∞控制器相似的控制效果，但需要注意的是LPV控制器是一个随参数时变的控制器，它能够在设计者所希望的飞行包线段内取得良好的控制效果。

图6 控制前后频域对照图Fig.6 The frequency domain control effect

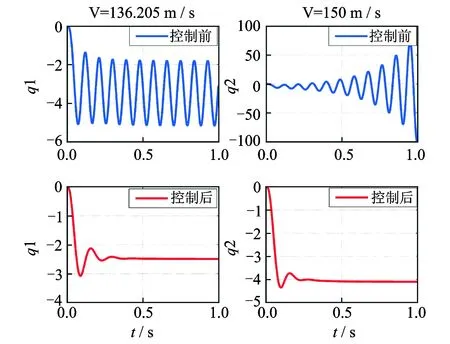
图7 控制前后时域对照图Fig.7 The time domain control effect

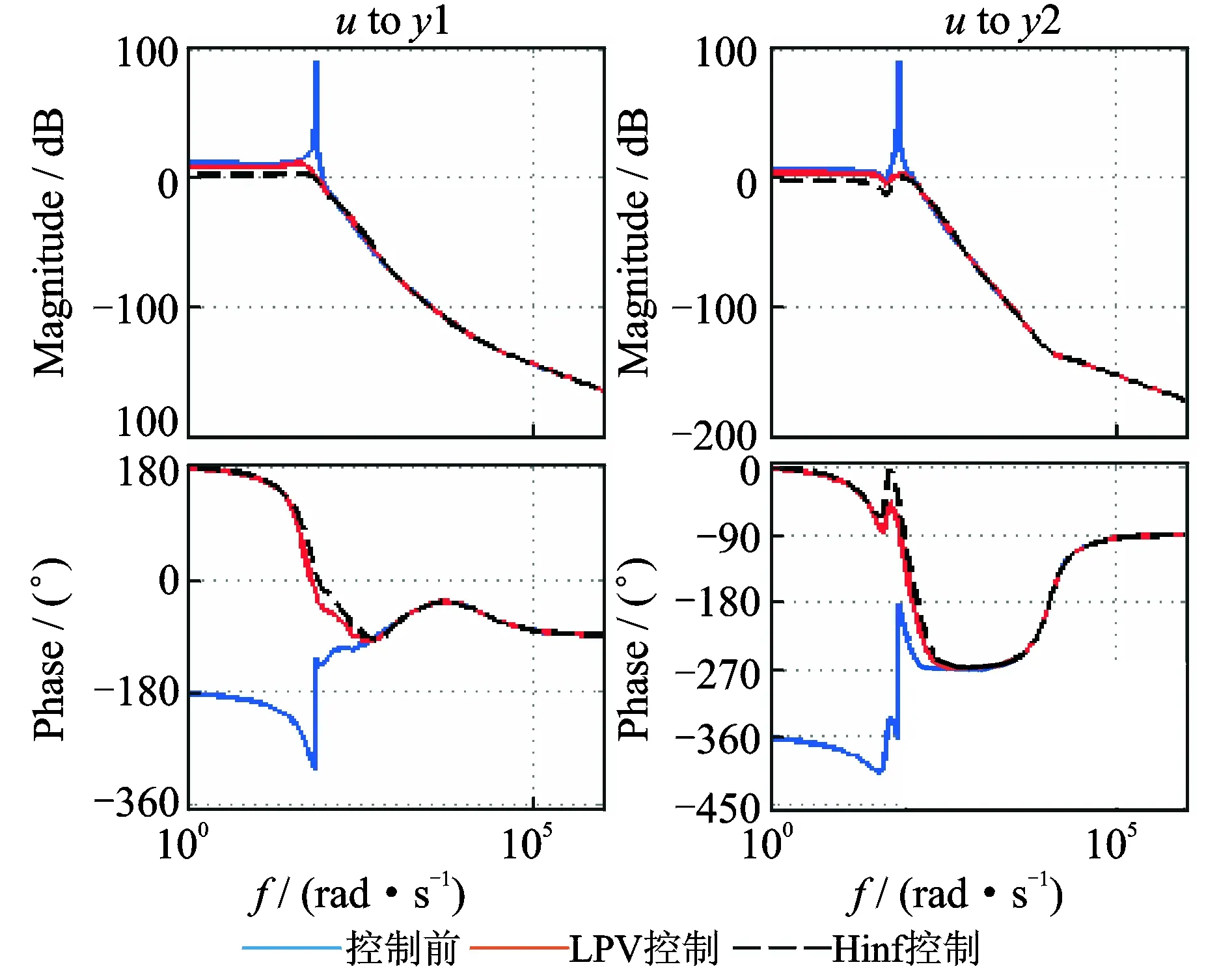
图8 LPV控制与Hinf控制对比Fig.8 LPV control versus Hinf control

5 结 论

本文利用LPV技术设计颤振主动抑制控制器。首先，针对高阶网格LPV模型，变参斜投影降阶法的计算量小，降阶效果好；采用基于Lyapunov函数的方法设计LPV控制器。针对92阶的Goland Wing模型，仿真结果表明降阶算法计算时间短，降阶模型与全阶模型的低频频率特性以及轻阻尼模态轨迹基本重合；最终，设计出的LPV控制器，在预期的飞行包线内能够有效抑振。

[1] Olds S D. Modelling and LQR control of two-dimensional airfoil[D]. Blacksbur:Virginia Polytechnic Institute and State University, 1997.

[2] Bail T R. A disturbance-rejection problem for a 2-d airfoil[D]. Blacksburg:Virginia Polytechnic Institute and State University, 1997.

[3] Martin R W. Robust multivariable flutter suppression for benchmark active control technology wind-tunnel model[J]. Journal of Guidance, Control, and Dynamics, 2001,24(1):147—153.

[4] Barker J M, Balas G J. Comparing linear parameter-varying gain-scheduled control techniques for active flutter suppression[J]. Journal of Guidance, Control, and Dynamics, 2000,23(5):948—955.

[5] Balas G J, Claudia M, Peter J S. Robust aeroservoelastic control utilizing physics-based aerodynamic sensing[C]. AIAA Guidance, Navigation, and Control Conference, Minneapolis, 2012:4897—4907.

[6] Arnar H, Peter J S, Balas G J. LPV aeroservoelastic control using the LPV tools toolbox[C]. AIAA Atmospheric Flight Mechanics (AFM) Conference, Boston, 2013:4742—4766.

[7] Andy P. Gain scheduling via linear fractional transformations[J]. Systems and Control Letters, 1994,22(2):79—92.

[8] Wu F. Control of linear parameter varying systems[D]. Berkeley: University of California, 1995.

[9] Sun X, Postlethwaite I. Affine LPV modeling and its use in gain-scheduled helicopter control[C]. UKACC International Conference on Control, Swansea, 1998:1504—1509.

[10] Tang W, Shi Z K, Chen J. Aircraft flutter modal parameter identification using a numerically robust least-squares estimation frequency domain[J]. Chinese Journal of Aeronautics, 2008,21(6):550—558.

[11] Tang W, Wu J, Shi Z K. Identification of reduced-order model for an aeroelastic system from flutter test data[J]. Chinese Journal of Aeronautics, 2017,30(1):337—347.

[12] Theis J, Seiler P, Werner H. Model order reduction by parameter-varying oblique projection[C]. American Control Conference, Boston, 2016:4586—4591.

[13] Wu F, Yang X H, Andy P, et al. Induced L2-norm control for LPV systems with bounded parameter variation rates[C]. American Control Conference, Anchorage, 2002:983—998.

[14] 孙智伟.高空长航时无人机多学科设计若干问题研究[D].西安：西北工业大学, 2016.

Sun Zhiwei. Investigation of the problems in multidisciplinary design of high altitude long endurance unmanned aerial vehicle[D]. Xi′an: Northwestern Polytechnical University, 2016.