一种融合时频信息的钢琴音符端点检测算法

黎思泉，王泓程，顾思恒，张杰霖，万永菁

（华东理工大学 信息科学与工程学院，上海 200237）

钢琴是“乐器之王”，钢琴学习者的数量也十分庞大。为了提高习琴者的学习效率，各式各样的钢琴陪练软件应运而生。为了能准确评价习琴者的演奏效果，必须采用有效的乐音识别技术提取出隐含在钢琴音频中的节奏和音符。

正确的音符端点检测是实现乐音识别的前提。文献[1]改进了短时能量算法，采用自适应阈值寻找音符段起始位置，该算法能够大致分割出不同的音符段。Masri[4]提出了一种对高频能量进行加权的算法，能够加强时域特征，使音符端点识别更加准确，但是，2种算法在识别大字组的音频时准确率比较低。Bello[3]等提出用相位特征来表征音符起始点，但仅对部分音频有较好的效果，在相位特征不够明显的乐谱中，检测准确率低于基于幅值的识别方法。

在端点的识别算法中，识别准确率更高的有基于距离的算法，比较有代表性的有基于短时傅里叶变换以及谐波结构计算频谱距离[4]和基于短时MFCC倒谱计算距离[5]。基于距离的算法能够有效切分音符，但是，钢琴由于自身谐波规律，识别某些频谱突变的和弦可能会导致同一个音符段被切分；在快节奏乐曲中出现2个连弹的相同琴键的情况下，也无法准确识别。

近年来提出了一些基于先验知识的识别算法，预先提取乐谱的音频特征，再与待识别钢琴音频进行校对得出音频的频域信息，从而实现音符切分，效果比较好的有采用改进的非负矩阵分解（Non-negative Matrix Factorization，NMF）提取音频特征的算法[6]和基于Chroma-based BOW特征的算法[7]。通过预先提取单音的频谱特征可有效识别音符起始点，但是，必须在识别钢琴曲音频前预先对钢琴曲的标准音频进行特征提取，准备工作量大。

针对钢琴乐音音符端点检测问题，本文提出了一种融合时频信息的算法，在能量峰值确定音符端点的基础上，利用频域的信息再进行端点筛选，并通过分析能量衰减的程度保证筛选的准确性。通过改进能够实现对大字组音频的准确识别，并且不需要先验知识，以准确地识别出音符起始点。

1 算法思想

算法首先基于音频帧能量突变信息进行端点预检测，然后依据音频键号频谱信息进行端点过滤，实现音符端点的精准切分。

1.1 基于时域音频帧能量突变信息的端点预检测

钢琴的音符能量来源于琴槌对琴弦的短时敲击，并经过钢琴腔体后传入人耳，因此，可将人耳感知到的钢琴音符视作一个短时能量脉冲。

首先对音频信号进行分帧处理，计算每一帧信号的绝对幅度平方和，获得每一帧信号的能量Ei，如式（1）所示：

式（1）中：si（m）为第i帧音频信号的第m个点的幅值；L为帧长，帧长的取值与采样频率相关，为了简化运算并保证准确率，通常取采样频率的1.5%～2%作为帧长。

然后，计算相邻两帧的能量差△Ei，如式（2）所示，即：

式（2）中：△Ei为音频帧能量的变化信息。

由于计算了帧与帧之间，而非点与点之间的能量差信息，△Ei其实已经过滤了一些原始音频信号中的微小能量起伏，对计算整体音频信息的能量变化起到了平滑的作用。此外，由于采用了差分运算，相邻两帧的能量差值△Ei比每一帧能量Ei更易用于音符起始点的判断，超过某一门限的△Ei的正峰值位置对应初始音符预测点。

钢琴曲《波尔卡舞曲》的乐谱片段和对应音频如图1所示，基于短时能量与短时能量求差值的检测函数如图2所示。

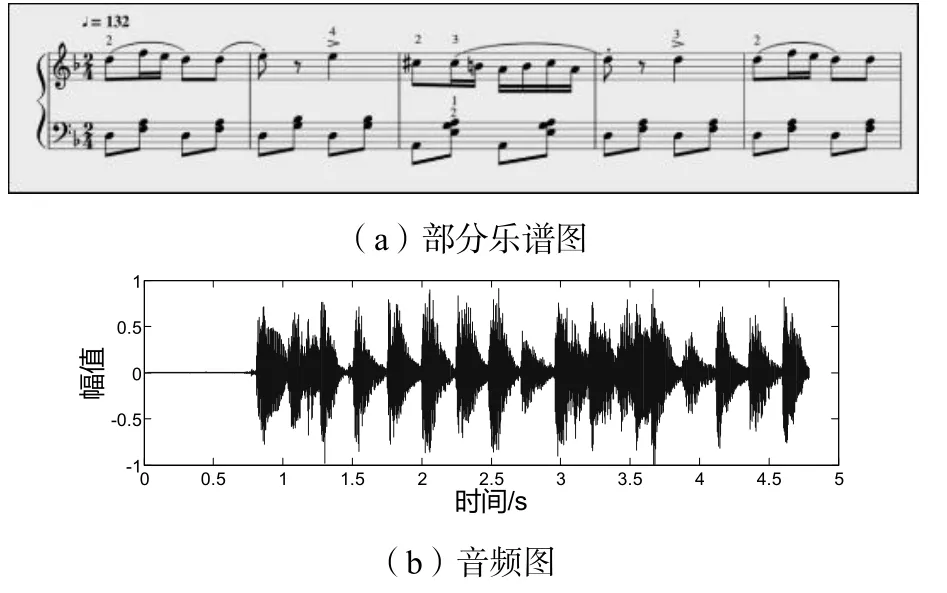
图1 钢琴曲《波尔卡舞曲》的乐谱片段和对应音频图

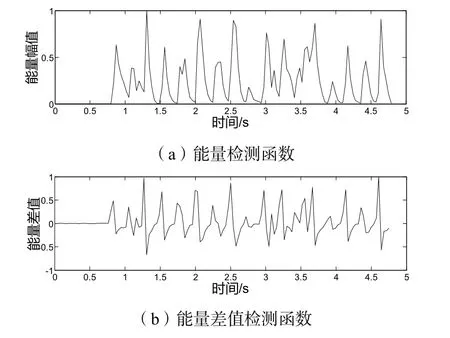
图2 基于短时能量与短时能量求差值的检测函数

为了避免初始音符预测点中存在相邻过近的伪预测点，本文采用以下步骤处理初始音符起始点：①求相邻两帧的能量差值△Ei的极大值，将△Ei＞0的极大值点标记为候选预测点，并存于集合A中；②寻找集合A中所有候选预测点的最大值，并标记此点为预测起始点；③寻找所有与步骤②中标记的预测起始点之间的距离小于D的候选预测点，将这些点从集合A中清除；④重复步骤②和步骤③，直至集合A中没有可以再标记的候选预测点为止。

在上述步骤中，D定义为相邻音符端点的最小间隔，计算公式为：

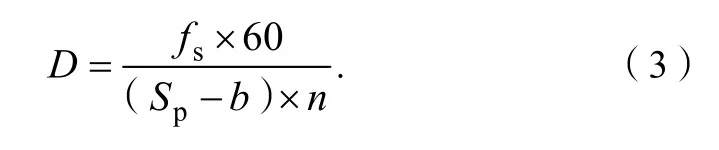
式（3）中：Sp为钢琴演奏的拍速，单位为“拍/分”；n为乐谱最小音符为n分音符；fs为采样频率；b为误差参数，b的取值与乐音的拍数有关，为了尽量降低预测过程的漏检率，b的取值通常在20～40之间。

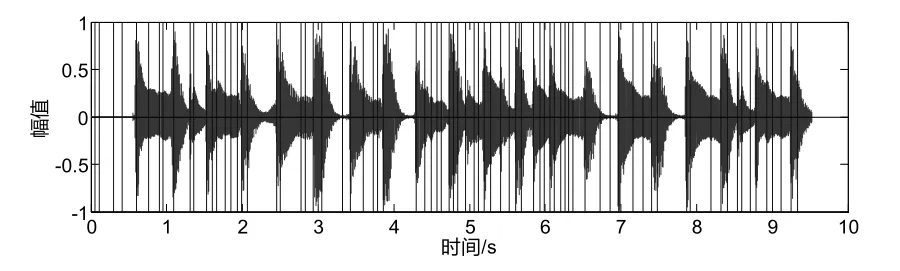
图3 基于检测函数极值点进行切分

图3是图1基于检测函数极值点进行音频切分所得图像，在没有进行极值点过滤时存在很多冗余点，经过上述步骤的处理，得出图4所切分图像，在保留所有可能的音符端点的前提下，过滤冗余点，但要保持音频处于过切分状态。

图4 过滤之后所得的极值点

1.2 基于音频键号频谱信息的音符端点过滤算法

基于音频帧能量突变信息的端点预检测可以保证在低漏检率下，提取出音频中的初始端点位置。但是，由于算法中的门限尺度较为宽松，这些预测的端点中仍有部分音符伪端点，需要进行二次滤除。本文基于音频键号频谱信息对初始音符端点进行过滤。钢琴琴键对应基频如图5所示。

图5 钢琴琴键分布图

由图5可知，每上升12个音高，基音频率将会加倍，即钢琴符合12平均率。每个琴键对应1个基频，第i个琴键的基频为fi，其公式为：

式（4）中：fi为第i号琴键的基频，1≤i≤88；f0＝440 Hz，是一个常数。

钢琴音频的谐波频率如式（5）所示，在基频为f的琴键音频中，第k次谐波频率fk的计算公式为：式（5）中：B为钢琴的不谐和系数，由琴弦的材料、长度等因素决定，一般介于50×10-6～1 000×10-6之间。

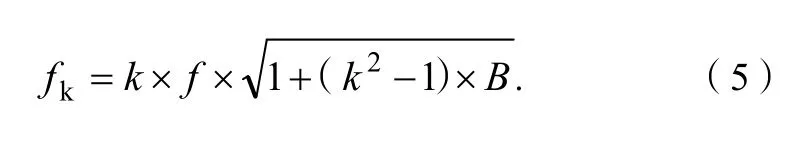
对相邻的2个初始音符端点之间的音频段进行傅里叶变换，得到其频谱A（f）。将音频段频谱A（f）按照钢琴基频规律归并为琴键键号对应的谱值A（i）。对应关系如式（6）所示：

然后，计算两相邻音频段的频谱特征相似度，即：

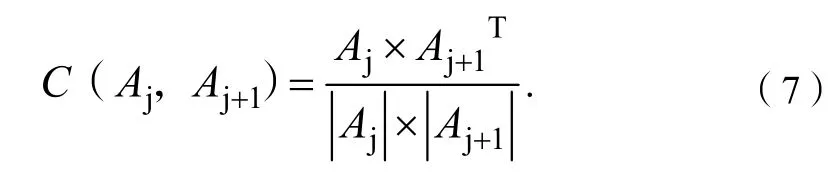
式（7）中：Aj和Aj＋1为相邻的2个音频段的键号谱值，均为 1×88 的一维向量；Aj＋1T代表Aj＋1进行转置。

当C（Aj，Aj＋1）为 1 时，说明Aj和Aj＋1两段音频谱特征完全相似；当C（Aj，Aj＋1）为 0 时，说明Aj和Aj＋1两段音频谱特征不相似。

新音符产生时，单个或部分音符频段的能量将会大幅上升，即频率特征中的部分元素将会发生突变，相似度值将会比较小，由此可以辨别两段音频是否有不同的音符频谱信息。钢琴音频在不改变触键音符时，会随着时间延长出现部分谐音甚至基频频谱成分衰减的情况，而在时域中又体现出一个能量的伪峰，极易造成音符端点错误切分。如图4中第一个音符被切分的情况，通过基于音频帧能量突变信息的端点预检测后，出现了第二根冗余的音符端点分割线。但是，由于琴键触键时间较长引起频谱成分衰减，第一段和第二段的键号频谱相似度也不大，仍然无法去除第二个冗余端点。

为了解决此问题，本文采用能量补偿的方法进行修正，即将前一个音频段的键号频谱减去后一个音频段的键号频谱，如果某一键号谱值的差值为正，将此差值补偿到后一段音频的对应的键号谱值中；如果某一键号谱值的差值为负，则不予补偿。计算补偿后的相邻音频段的键号频谱相似度，并以此相似度的值判断后一段音频端点是否为伪端点。如图6所示，通过键号谱值补偿，前后2个音频段的相似度极高，即可判定为2个音符的触键键号是一致的。

图6 切分了同一个音符段相邻音频的补偿前后的频谱特征

当连续2个相同的按键出现时，余弦相似度的计算就会过滤掉正确的音符起始点，如图7所示，钢琴曲《小星星》的前2个音符是一样的，连续敲击相同琴键，所得两段音频的频谱特征一定是相似的。为了避免误删除相邻音符触键相同的音频端点，本文采用基于相邻音频键号频谱的曼哈顿距离的音频端点修正算法。

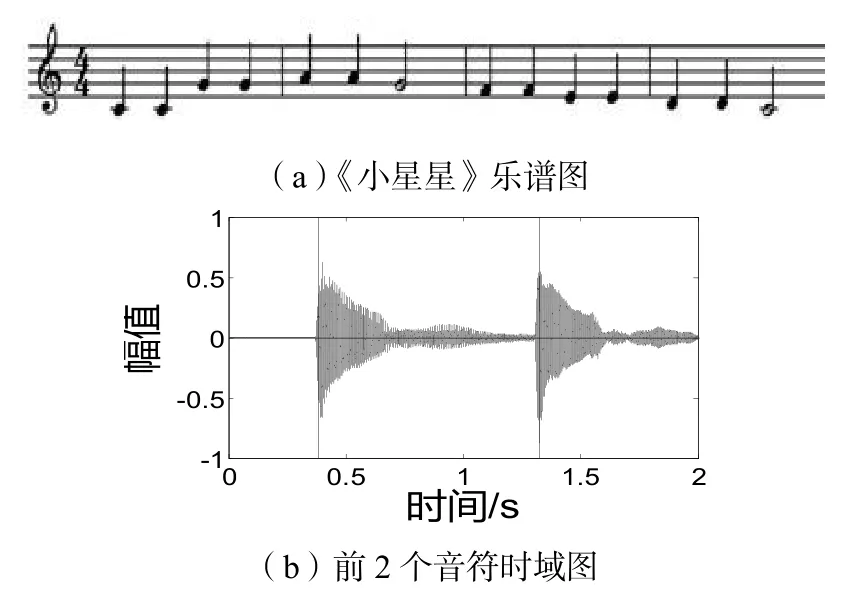
图7 《小星星》部分乐谱以及前2个音符的音频时域图

无法用相似度区分的相邻音频段能量分布如图8所示。

图8 无法用相似度区分的相邻音频段能量分布

相邻音频键号频谱的曼哈顿距离为：

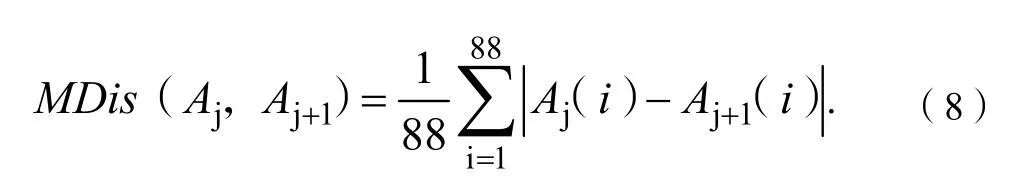
本文取相似度门限为Si，曼哈顿距离门限为Di。当相邻音频的键号频谱相似度大于Si时，再进行曼哈顿距离的验证。如果曼哈顿距离小于Di，说明能量衰减程度比较低，有新的音符按下，则不删除该音符端点；反之，如果曼哈顿距离大于Di，则判定能量衰减了，两段音频为同一个音符段，删除该冗余端点。经过多次实验发现，Si取0.94～0.96，Di取0.04～0.08为宜。

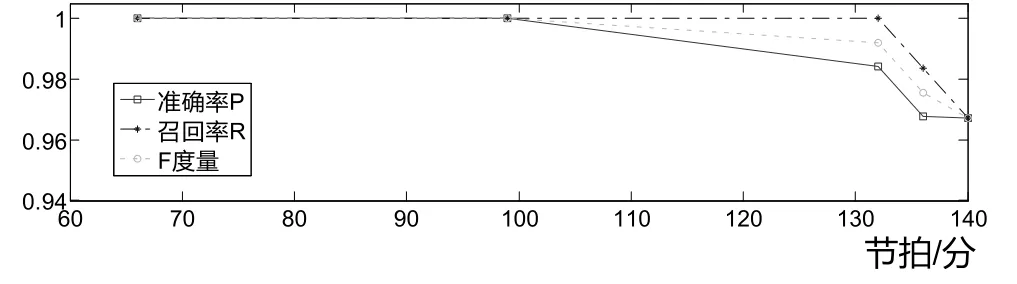
图12 不同节奏下钢琴曲《波尔卡舞曲》的评价参数

2 实验结果与分析

图9和图10是经过余弦相似度和曼哈顿距离筛选之后的切分音频图，图4是筛选之前的切分音频图，对应图1和图7中的乐谱，可以确定在经过音符端点的筛选之后，有效滤除错误的音符端点。

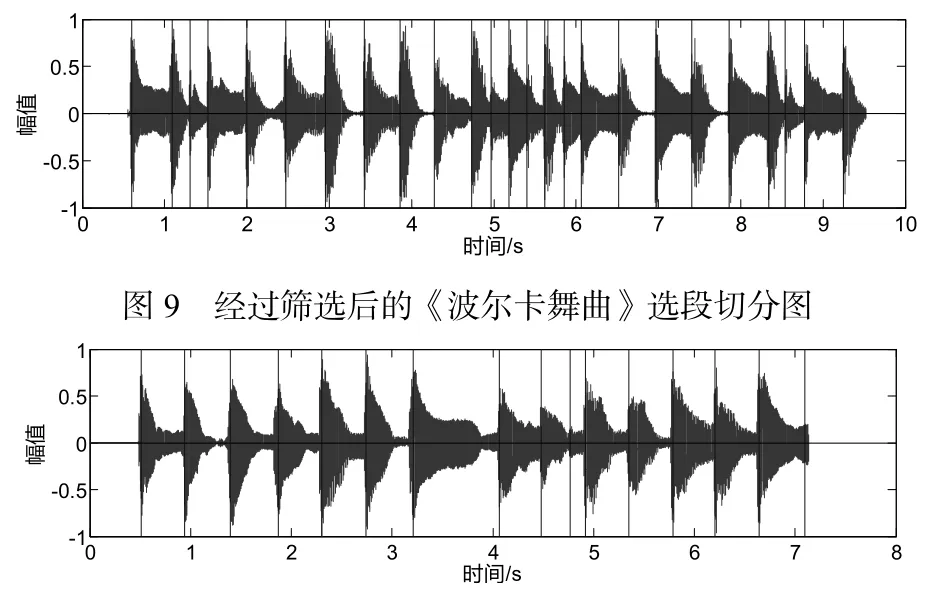
图10 经过筛选后的《小星星》选段切分图

本文采用准确率P（Precision）、召回率R（Recall）和F度量（F-Measure）等指标评价音符端点的识别效果。其中，F度量是结合准确率与召回率的一个综合性评价指标。准确率P、召回率R和F度量3个指标公式为[8]：

式（9）（10）（11）中：Ncorrect为检测出的正确音符个数；Nmiss为在检测过程中遗漏的未被检测出来的音符个数。

图11和图12为采用本文算法对不同节拍乐曲进行识别的效果评价。从图11和图12中可以看出，本文算法对钢琴曲《波尔卡舞曲》和《小星星》识别的F度量参数在95%以上，在不同节奏的端点检测中有较好的准确率和召回率。对比图11和图12，《小星星》的端点检测效果不如《波尔卡舞曲》，原因在于本文基于余弦相似度进行筛选，小星星乐谱中出现过多的重复音符，在一定程度上影响了识别效果。图10是138拍每分钟的一段《小星星》音频切分图，对照图7中的乐谱图，第9个音符被切分成两段，在快节奏按压琴键时，音符衰减不明显，曼哈顿距离判断衰减的难度比较大。识别乐曲中有较多重复音符会影响识别准确率，对于一般音频可以保证较高的准确率。在重复音符的影响下，对音频进行端点检测的准确率和召回率仍能保证在95%以上。

图11 不同节奏的钢琴曲《小星星》的评价参数

3 结论

本文算法融合时频信息，基于时域能量进行端点预检测，找出能量差值突变的点作为预检测的端点，通过频域分析筛除过切分的音符端点。运用本文算法进行端点检测，在不遗漏音符端点的基础上能够有效减少识别错误的音符端点。实验表明，对不同节奏的音频进行端点检测，本文算法能够保证有较好的检测效果。

［1］卞毓伟，郭玲.基于权值分配的音符识别研究［J］.计算机与现代化，2017（3）：122-126.

［2］Rodet X，Jaillet F.Detection and Modeling of Fast Attack Transients［J］.Proceedings of the Icmc01 La Habana，2001（12）.

［3］Bello J P，Sandler M.Phase-based note onset detection for music signals［C］//IEEE International Conference on Acoustics，Speech，and Signal Processing.Proceedings，IEEE，2003：441-444.

［4］Masri P.Computer Modeling of Sound for Transformation and Synthesis of Musical Signals［D］.Bristol：University of Bristol，1996.

［5］卞毓伟.钢琴弹奏乐曲识别算法研究及其APP设计与实现［D］南京：南京理工大学，2017.

［6］万玉龙，王宪亮，周若华，等.基于非负矩阵分解的钢琴多音符估计［J］.网络新媒体技术，2014，3（5）：23-27.

［7］张秀，李念祖，李晓强，等.基于Chroma-based BOW特征的多版本音乐识别［J］.小型微型计算机系统，2015，36（2）：397-400.

［8］陈雪梅.乐音信号的多基频估计［D］.济南：山东大学，2014.