考虑侧面摩擦的侧限压缩模型的数值解法

, *, ,

(1.南京水利科学研究院 岩土工程研究所，南京 210029；2.北京大学 数学系，北京 100871)

1 引 言

侧限压缩模型是指材料在不发生侧向变形条件下的受力模型。小型的侧限压缩模型(如侧限压缩试验)一般不必考虑侧面摩擦作用[1]，但在一些较大尺寸的工程条件下，侧壁摩擦不能忽略。如海上防波堤[2,3]以及海上风电机[4,5]等箱筒型基础结构，其下沉到位后，舱内土体的受力及沉降计算可以看作内部土体受筒壁侧限作用的问题，且应考虑侧壁摩擦的影响。

图1为江苏响水海上风电复合筒型基础下沉到位后的受力示意图[6]，结构所受的重力、浮力、端阻力、侧壁阻力和地基反力构成平衡力系。单独分析下部钢筒结构的每个隔舱，其内部土体均处于存在侧面摩擦的侧限压缩状态。结构自重引起的附加应力增加了侧壁的水平应力，进而对侧壁的摩擦力产生了影响；摩擦力的变化也影响着土体内部的应力变化。两者存在的耦合关系是分析问题的难点。

筒体外部的侧土压力计算只需考虑土体自重，但舱内侧土压力和土体变形的计算需要考虑土体自重、外荷载和侧壁摩擦的共同作用。模型在受力和变形计算时，主要是考虑土体自重和外荷载作用[7]，而常忽略由侧壁摩擦产生的影响，从而带来一定的计算误差。因此，对于存在摩擦的侧限压缩模型，能更准确地计算结构受力和土体变形，具有一定的理论和工程实际意义。

2 侧限压缩模型的理论难点

重力作用引起的侧土压力分布的计算较为简单，因此本文重点分析由外荷载产生的侧壁摩擦力对受力和变形的影响。另外，土是多孔介质，其本构有着非线性非弹性的特点[8]，但考虑到实际工程中隔舱内部土体的实际变形较小，可将此阶段的变形近似看作是弹性变形，从定性研究的角度，将土体复杂的变形问题进行简化。由此对模型做如下假设。

(1) 底面无摩擦，两侧摩擦为库仑摩擦[9,10]。

(2) 内部土体为弹性变形，暂不考虑自重。

根据荷载作用方式的不同，可以将侧限压缩模型分为刚性荷载侧限压缩模型与柔性荷载侧限压缩模型两类。刚性荷载是指通过刚性基础施加的荷载[11]，可通过在土体上部增加一个刚性光滑盖板来实现；柔性荷载概念与之相似，相当于直接加载，荷载条件的选取可由具体工况确定。如图2所示(为研究方便，对结构进行了倒置)，其中上部荷载为P，土体高度为H，宽度为2L。

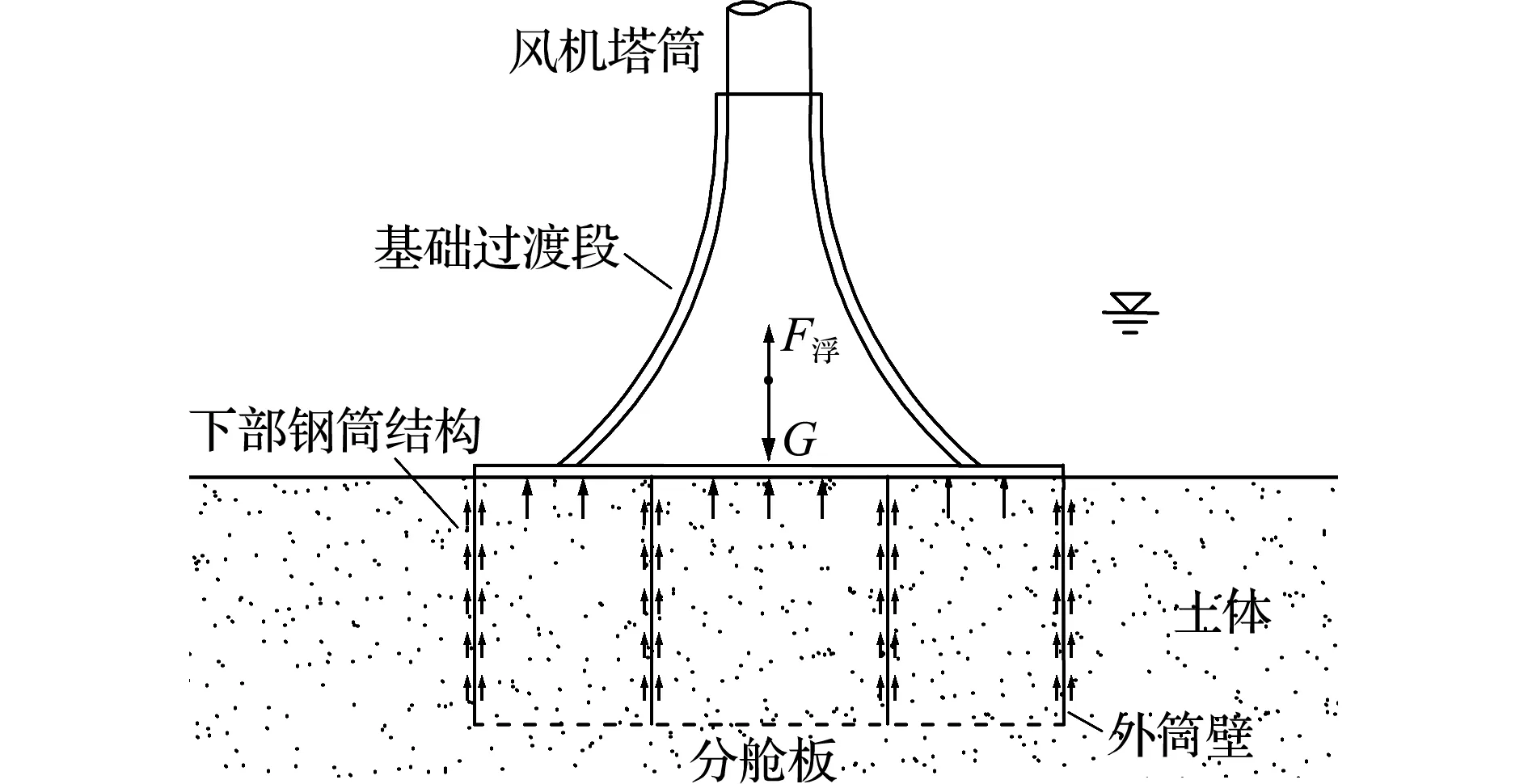
图1 海上风电基础受力示意图

Fig.1 Force diagram of offshore wind turbine foundation

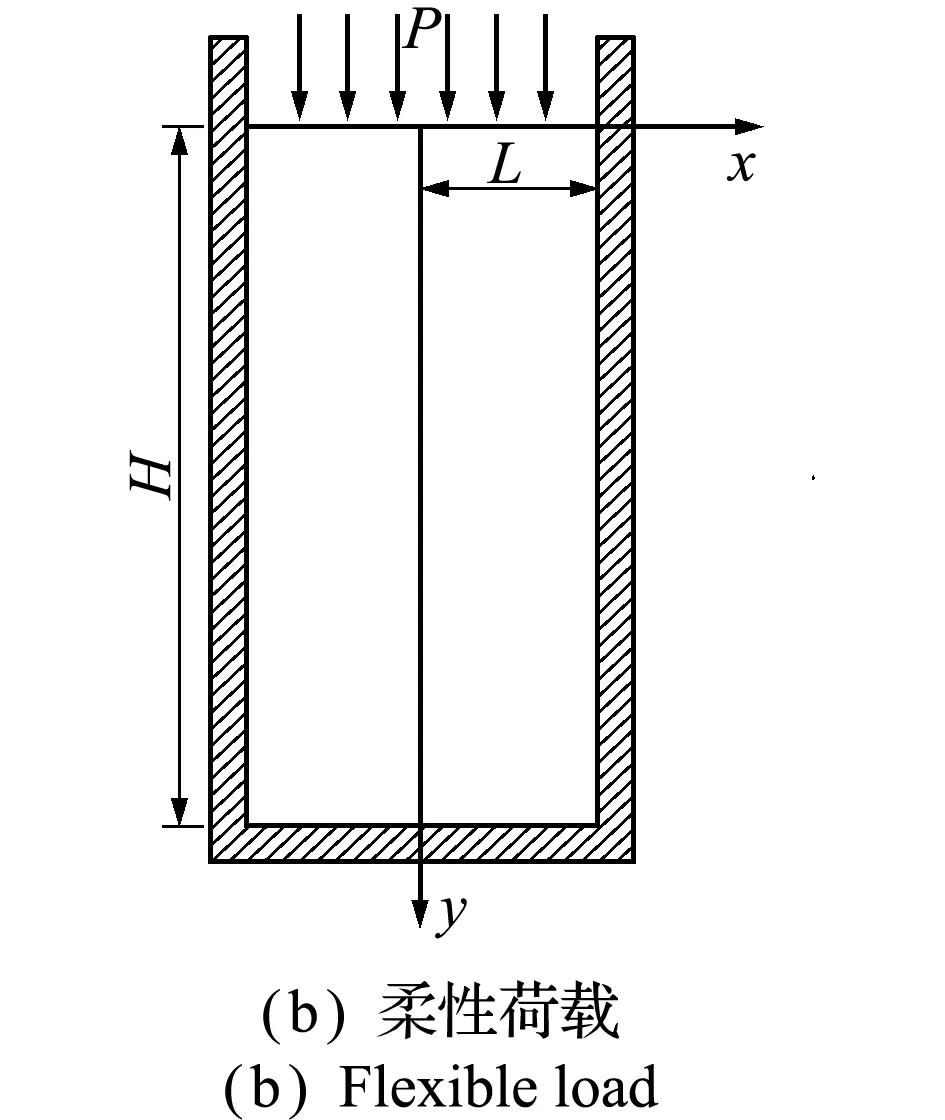
图2 两种不同荷载条件的侧限压缩模型

Fig.2 Two different loading conditions of confined compression models

根据弹性力学原理[12]，侧限压缩模型问题的平衡微分方程组为

(1)

式中u和v分别为水平和竖向位移；σx,σy和τx y分别为水平向应力、竖向应力和切应力；ν为土体泊松比。

其位移边界条件为

(2)

应力边界条件包括荷载边界条件和摩擦边界条件。对于荷载边界条件，刚性荷载条件下为

(3)

柔性荷载条件下为

(σy)y = 0=-P

(4)

本问题的计算难点在于摩擦作用下的应力边界条件。由于摩擦作用，模型两侧的正应力与切应力满足库仑摩擦定律[13,14]，存在的关系为

(τx y)x = ± L≤μ(σx)x = ± L

(5)

式中μ为摩擦系数。此处的边界条件是存在变量耦合的边界条件[15]，而且不等式约束无法作为定解条件。仍需做如下假定，平衡状态下，侧面上的切应力和水平应力应尽量满足库仑摩擦公式(τx y)x = ± L=μ(σx)x = ± L，即两者应当充分接近。现构造目标泛函

(6)

以衡量侧面上水平应力函数与切应力函数之间的距离，则可得定解条件(τx y)x = ± L和(σx)x = ± L，使得δ达到最小。

综上，侧限压缩模型的摩擦边界条件不是常规的三类边界条件，直接求解问题的解析解比较困难，因此本文拟结合摩擦边界条件的特点，构造迭代方法求出方程的数值解。

3 迭代法求解过程

对于实际问题，可以认为偏微分方程组的解是存在的，考虑结构的对称性，可设边界x=±L处切应力τx y和水平应力σx函数分别为

(7)

即将问题转化为求解适当的f和g，使得δ达到最小。方程求解的大致步骤如下。

(1) 取迭代初始函数g0(y)，默认取g0(y)=0。

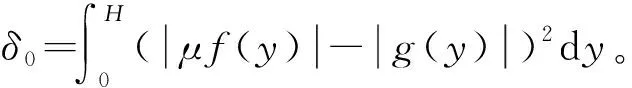
(3) 更新g(y)。由切应力互等定理知g(0)=g(H)=0。此外，参考库仑摩擦定律，令其他采样基点处的值满足g(y)=μf(y)，插值得到g1(y)。

(4) 重复步骤(2，3)，直至收敛。收敛判断条件为δi-δi -1<ε，其中ε为给定的阈值。

其中每步求得的方程解未必能用初等函数表示，但可选取适当的拟合函数作为迭代函数的近似。对于本问题，采用多项式插值就可以达到较高精度(此处采用9次多项式)。需要注意的是，经实际计算发现，如果采用均匀的插值基点，可能会出现龙格现象，即插值多项式在端点处会发生较大波动，从而影响计算精度，故建议选取切比雪夫插值基点[16]，可以有效缓解龙格现象。以上计算过程可通过数学软件编程实现。

4 计算结果分析

本文选取了一个柔性荷载的算例来对迭代法的计算结果进行分析，具体参数列入表1。

首先，分别输出5次迭代后接触侧面上的水平应力分布，如图3(a) 所示。初始迭代函数g0(y)=0，相当于无摩擦的侧限压缩，故水平应力第一次计算结果为定值。随着g(y)的更新，水平应力函数渐渐收敛到一个稳定的曲线，f(y)在4次迭代之后基本保持不变，说明迭代法求解是可行的。

其次，针对不同的初始迭代函数，得到目标泛函δ与迭代次数的关系，如图3(b)所示。如前文所述，若目标泛函呈现递减趋势且趋于稳定，则计算收敛。可以看出，三种不同的初始迭代函数，虽对应的目标泛函初值有所不同，但都有着较高的收敛速度，并且都在4次迭代后趋于稳定，稳定值近似为0，说明接触侧面上的正应力与摩擦应力基本满足τx y=μσx这一关系。

表1 各项参数设定

Tab.1 Parameters setting

quantityvalueElastic modulus/MPa10Poisson’s ratio0.3Height/m4Width/m2Friction coefficient0.3Load/kPa100Quantity of interpolating points31

图3 迭代法收敛性分析

Fig.3 Convergence analysis of iterative method

综上，本文的函数迭代方法受初始迭代函数影响较小，计算结果较为稳定，且收敛速度较快。

利用ABAQUS有限元分析软件，对同等条件下的侧限压缩模型进行计算。将实际工程中关心的侧面水平应力和土体表面沉降计算结果进行对比分析，如图4所示。可以看出，两种方法的计算结果高度一致，接触侧面的水平应力值仅在边角处存在少许差异，土体表面位移的最大误差也仅为0.1%，说明两种计算方法都是可行的，但相对于侧重具体问题分析的数值模拟方法，侧重理论计算的迭代方法不仅计算速度更快，而且更具普遍意义，还可推广应用于其他存在耦合边界条件的偏微分方程数值求解中。

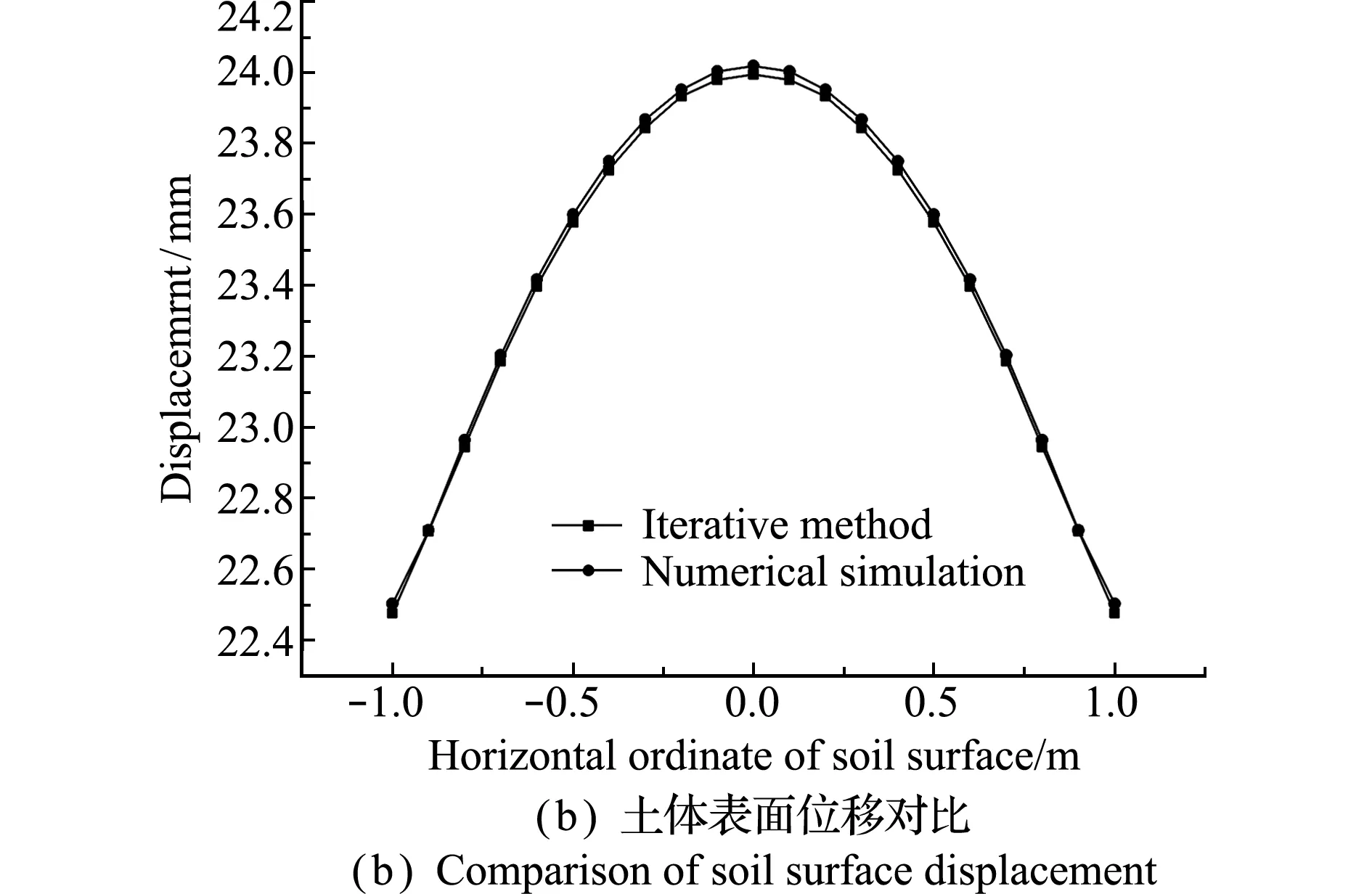
图4 迭代法与数值模拟计算结果对比

Fig.4 Calculation results comparison of iterative method and numerical simulation

如图4(a)所示，在接触侧面上，由荷载引起的水平应力并非线性分布，而是呈倒S型分布，随着深度的增加，水平应力先增加，后减小，再增加，中间阶段的递减趋势主要是由于摩擦力抵消了一部分荷载。

如图4(b)所示，受两侧摩擦力影响，土体表面位移也不均匀，中间沉降较大，两侧沉降较小，即变形后土体表面呈凹陷状。

5 结 论

(1) 即便对侧限压缩模型问题进行简化，由于其摩擦边界条件存在变量耦合的约束条件，在解析求解时仍存在一定的困难，而采用函数迭代方法是一个可行的思路。

(2) 总体而言，迭代方法收敛速度较快，且计算过程较为稳定，与ABAQUS的数值计算结果一致性较高。此外，该方法对其他存在变量耦合边界条件的偏微分方程的数值求解有一定的借鉴价值。

(3) 计算结果表明，由荷载引起的水平应力和土体表面位移均呈现非线性分布，在实际工程计算时应给予充分考虑。

:

[1] 孟伟超,罗 强,蒋良潍,等.环壁摩擦力对固结试验压缩变形的影响分析[J].武汉理工大学学报,2014,36(8):104-109.(MENG Wei-chao,LUO Qiang,JIANG Liang-wei,et al.Analysis of ring-wall friction effect of consolidation container on the compression deformation in consolidation test[J].JournalofWuhanUniversityofTechnology,2014,36(8):104-109.(in Chinese))

[2] 蔡正银,徐光明,顾行文,等.波浪荷载作用下箱筒型基础防波堤性状试验研究[J].中国港湾建设,2010,69(s1):90-94,99.(CAI Zheng-yin,XU Guang-ming,GU Xing-wen,et al.Behavior investigation on a cylindrical breakwater during wave loading [J].ChinaHarbourEngineering,2010,69(s1):90-94,99.(in Chinese))

[3] 肖 忠,王元战,及春宁.基于极限平衡法的箱筒型基础防波堤稳定性分析[J].岩土工程学报,2013,35(5):828-833.(XIAO Zhong,WANG Yuan-zhan,JI Chun-ning.Stability analysis of bucket foundation breakwaters based on limit equilibrium method [J].ChineseJournalofGeotechnicalEngineering,2013,35(5):828-833.(in Chinese))

[4] 闫澍旺,霍知亮,孙立强,等.海上风电机组筒型基础工作及承载特性研究[J].岩土力学,2013,34(7):2036-2042.(YAN Shu-wang,HUO Zhi-liang,SUN Li-qiang,et al.Study of working mechanism and bea-ring capacity behavior of bucket foundation for offshore wind turbine [J].RockandSoilMechanics,2013,34(7):2036-2042.(in Chinese))

[5] 刘永刚.海上风力发电复合筒型基础承载特性研究[D].天津大学,2014.(LIU Yong-gang.Bearing Characteristics of Composite Bucket Foundation for Offshore Wind Turbine [D].Tianjin University,2014.(in Chinese))

[6] 练继建,贺 蔚,吴慕丹,等.带分舱板海上风电筒型基础承载特性试验研究[J].岩土力学,2016,37(10):2746-2752.(LIAN Ji-jian,HE Wei,WU Mu-dan,et al.Experimental study of bearing characteristic of bucket foundation of offshore wind turbine with bul-kheads [J].RockandSoilMechanics,2016,37(10):2746-2752.(in Chinese))

[7] 王元战,肖 忠,迟丽华,等.筒型基础防波堤稳定性简化计算方法[J].岩土力学,2009,30(5):1367-1372.(WANG Yuan-zhan,XIAO Zhong,CHI Li-hua,et al.A simplified calculation method for stability of bucket foundation breakwater [J].RockandSoilMechanics,2009,30(5):1367-1372.(in Chinese))

[8] 梅国雄,宰金珉,赵维炳.土体侧限压缩模量简易计算方法及其应用[J].岩土力学,2003,24(6):1057-1059,1064.(MEI Guo -xiong,ZAI Jin-min,ZHAO Wei-bing.A simplified calculation method of oedometric modulus of soil and its application [J].RockandSoilMechanics,2003,24(6):1057-1059,1064.(in Chinese))

[9] Potyondy J G.Skin friction between various soils and construction materials[J].Géotechnique,1961,11(4):339-353.

[10] 梁 越,储 昊,卢孝志,等.钢-土界面剪切规律时效性室内试验研究[J].水利水运工程学报,2015(1):28-32.(LIANG Yue,CHU Hao,LU Xiao -zhi,et al.Experimental studies on time effect of shearing characteristics of steel-soil interface [J].Hydro-ScienceandEngineering,2015(1):28-32.(in Chinese))

[11] 吕亚茹,丁选明,孙 甲,等.刚性荷载下现浇X形桩复合地基极限承载力特性研究[J].岩土力学,2012,33(9):2691-2696,2703.(LÜ Ya-ru,DING Xuan-ming,SUN Jia,et al.Analysis of ultimate bearing capacity of X-section cast-in-place concrete pile composite foundation under rigid load [J].RockandSoilMechanics,2012,33(9):2691-2696,2703.(in Chinese))

[12] 徐芝纶.弹性力学(第五版)[M].北京：高等教育出版社，2016.(XU Zhi-lun.Elasticity(5t hEdition)[M].Beijing:Higher Education Press,2016.(in Chinese))

[13] 罗晓明,齐朝晖,孔宪超.平面棱柱铰内考虑摩擦效应的接触分析[J].计算力学学报,2012,29(3):387-392.(LUO Xiao-ming,QI Zhao -hui,Kong Xian-chao.Non-colliding contact analysis with friction in the planar prismatic joint [J].ChineseJournalofComputationalMechanics,2012,29(3):387-392.(in Chinese))

[14] Lehane B M,White D J.Lateral stress changes and shaft friction for model displacement piles in sand[J].CanadianGeotechnicalJournal,2005,42(4):1039-1052.

[15] 张晓军,杨树生,李珊珊,等.耦合边界条件下Sturm-Liouville问题的渐近展开[J].内蒙古师范大学学报(自然科学汉文版),2016,45(6):749 -752,756.(ZHANG Xiao -jun,YANG Shu-sheng,LI Shan-shan,et al.The asymptotic expansion of Sturm-Liouville problem with coupled boundary condition [J].JournalofInnerMongoliaNormalUniversity(NaturalScienceEdition),2016,45(6):749-752,756.(in Chinese))

[16] Sauer T.NumericalAnalysis(2n d)[M].New Jersey:Addison-Wesley,2012.