直管振动流动传热特性数值模拟

孙 征，王宏光，韩铁鹰

(1.上海理工大学能源与动力工程学院，上海 200433；2.上海市动力工程多相流动与传热重点实验室，上海 200093；3.中电投珠海横琴热电有限公司，广东 珠海 519031)

换热器广泛应用于汽车冷却系统中，是水冷式冷却系统的重要部件[1]。由于路面颠簸等原因，汽车换热器工作在振动状态下，通过对振动状态下传热问题的研究，分析振动对传热性能的影响，对了解换热器的性能，改进换热器设计，降低汽车能耗有积极的意义。

文献[2,3]对管内流体流动引起的振动特性进行研究，指出管内流体的流动会引起管道的振动，流体的速度较小时，产生的动力对振动影响会很小，但是随着流体流速的增大这种影响会随之增大，当流体流速增大到某一临界值时，将会导致管道动力的失稳。文献[4]研究了机械振动对传热的影响，结果表明振幅较小振动频率较大时，振动使传热强度降低，传热效果最高下降20%。文献[5]分析了振动的原因及流体诱导振动的原理，在对壁面振动的模拟中采用 UDF定义圆柱面振动方程，指出振动可以加强传热。文献[6]研究了振动对管带式散热器空气流动和温度场的影响，指出随着振动频率和振幅的增大，换热性能得到提升。文献[7]等采用动网格技术研究了振动对换热圆管的传热特性的影响，并进行了场协同分析，指出振动能强化传热，并且其传热效果随振动频率和振幅的增加而增加，在同一振动参数下，雷诺数越小，强化效果越好。但是有关管道在非惯性坐标系下的正弦往复运动，对管内流体流动及传热特性影响的研究还不多见。

本文针对文献[7]的研究模型，采用UDF在简谐振动的非惯性坐标系下，模拟管道的振动，避免采用动网格技术，重点研究管子长度变化时振动对管内流体流动及传热特性的影响。

1 计算模型

原模型流动区域长600 mm，管径20 mm(见图1)。现模型计算区域长2 000 mm，管径20 mm(见图2)。左侧壁面为速度入口边界条件，速度为u，入口处流体温度为293 K；右侧壁面是压力出口边界条件，p=0；上下壁面为运动壁面，与管内流体进行对流换热，采用恒温壁面，温度为333 K，振动速度规律为[8]

v=2πfAsin(2πft)

(1)

式中f—频率；A—振幅；t—时间。

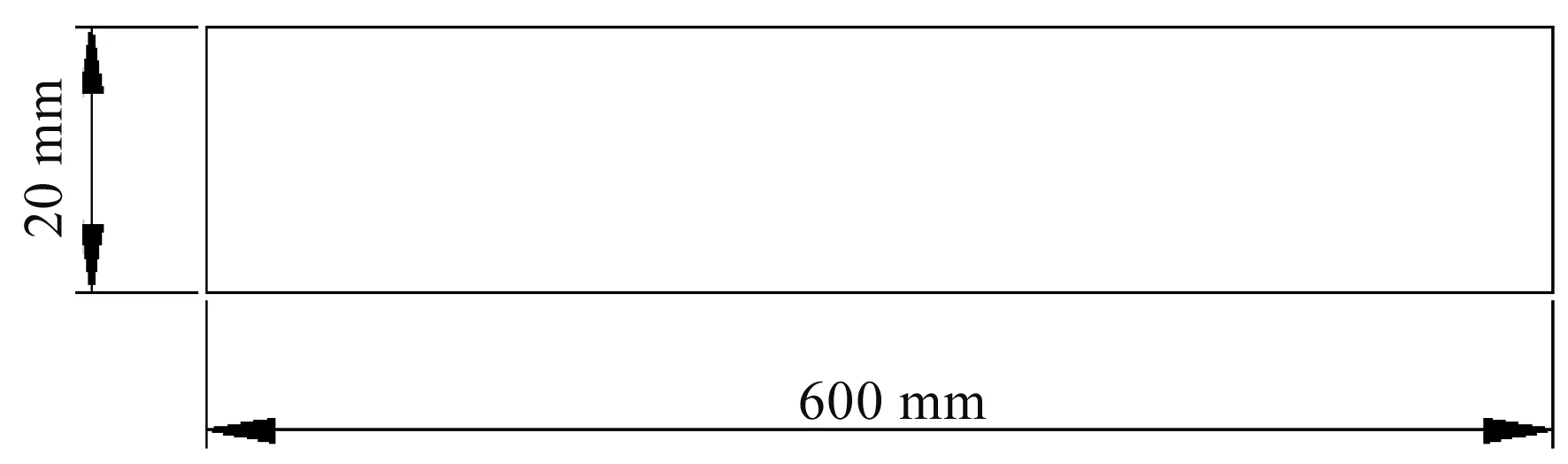
图1 原模型计算区域

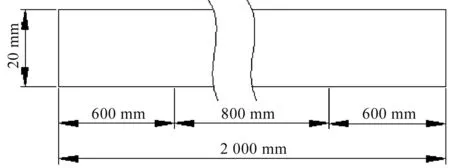
图2 现模型计算区域

根据换热器的流速特点，u值分别取为0.02， 0.04，0.06，0.08，0.10 m/s；汽车在行驶过程中换热器做随机振动，其振动包含多种频率成分。频率f选取为2，4，6，8，10 Hz；振幅A的选取主要是考虑了路面颠簸程度及换热器安装时与车体之间的空间限制，最终选取值为1，2，3，4，5 mm。

近壁面计算网格如图3所示，全部采用结构化网格，结合Y+的查询及探究[9]，通过来流速度确定第一层网格高度。计算求解器选定为非稳态隐式法，压力速度耦合采用PISO算法，选择二阶迎风格式，网格数量10万个，时间步长取0.01 s。

直管振动位移和速度边界条件通过UDF来控制，采用非惯性坐标系，圆管整体在非惯性坐标系内做与管道轴线方向垂直的简谐振动，网格随着圆管整体运动且无形变，振动方向与管道轴线方向垂直[10]。

图3 近壁面计算网格

振动直管计算参数见表1。

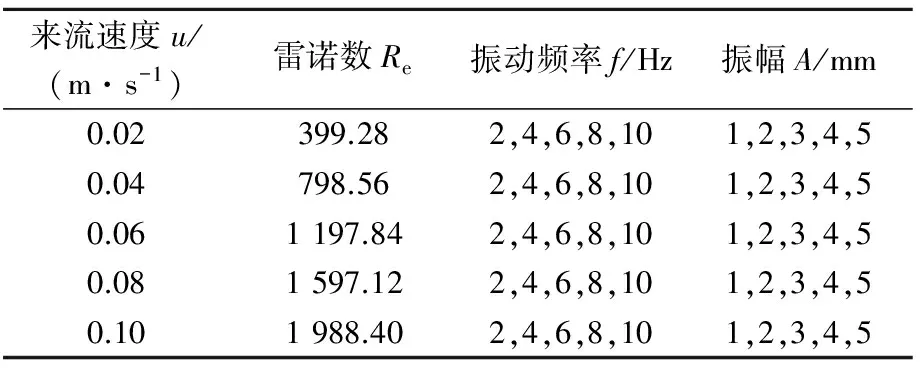
表1 振动直管计算参数

2 计算结果与分析

2.1 数值计算结果

振动圆管内努塞尔数为

(2)

式中λ——流体介质热导率；qw——平均热流密度；L——直管当量直径；Tw——壁面平均温度；Tf——流体平均温度。

图4为不同雷诺数时不同振幅下Nut/Nu随振动频率的变化。图4中，Nus为换热管静止时的壁面平均努塞尔数，Nut为换热管振动时的周期壁面平均努赛尔数。采用与吴艳阳相同计算方法及参数，得出相同的结论。由于振动外力的作用，边界层中惯性力影响大于粘性力[11]，振动能强化传热，并且传热效果随振动频率和振幅的增加而增加，在半周期内，时相位为90°时管内传热性能最好，在同一振动参数下，雷诺数越小，强化效果越好。

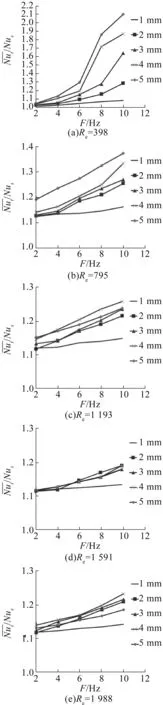
图4 Nut/Nus与振幅A的关系

图5为不同雷诺数时不同振幅下Nut/Nus随振动频率的变化关系。从图5中可以看出，直管在振动条件下，有强化换热效果，传热强度最高可以提高600%。Re=1 988时，比较发现，在相同频率和振幅的情况下，雷诺数越大，强化换热效果越好；在相同雷诺数下，雷诺数越小，振幅和振动频率对换热强度的影响越明显。Re=398时，以频率为2 Hz时的换热强度为基础，振幅为1 mm和2 mm时，换热强度随着频率增大而减弱，最多减弱18.3%，振幅在3 mm及以上时，换热强度随着频率增大而提高，最高可以提高76.6%；Re>398时，在以振动频率为2 Hz时的换热强度基础上，换热强度随着频率的增大而减弱。Re=1 988时，换热强度波动范围在5%以内。

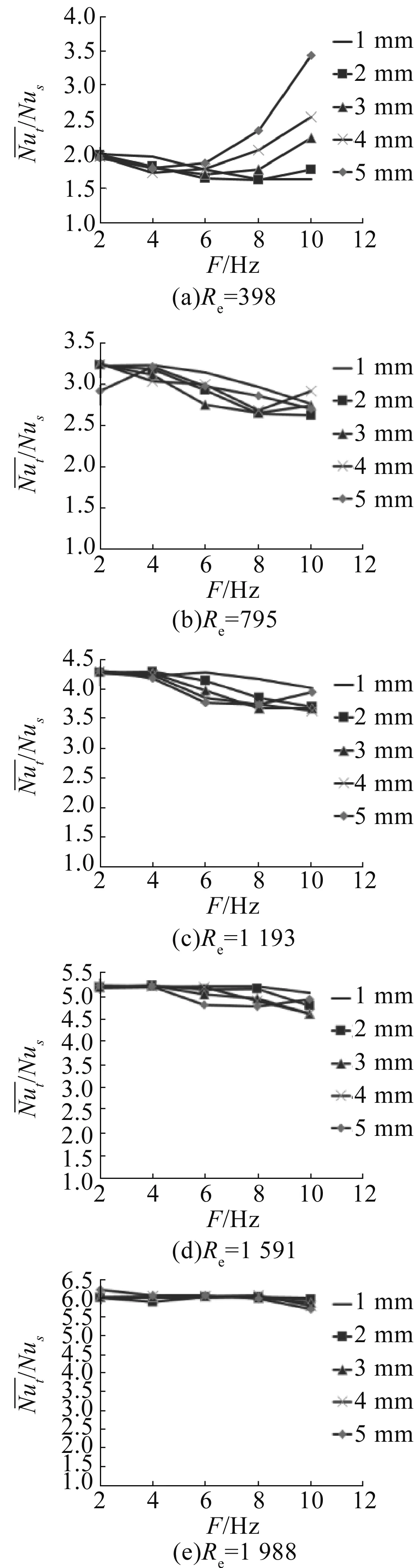
图5 Nut/Nus与振幅A的关系

2.2 强化传热原因分析

图2模型分为三段，第一段和第三段长度取600 mm，第二段长度取800 mm。

图6为第一段不同雷诺数时不同振幅下随振动频率的变化。由于振动外力的作用，边界层中惯性力远大于粘性力，流体边界层遭到破坏，流体流动状态明显改变，换热强度得到提高。Re=398和Re=795时，换热强度随着振动频率的增大而提高，最高400%；Re>795时，换热强度受振动频率和振幅的影响减弱。

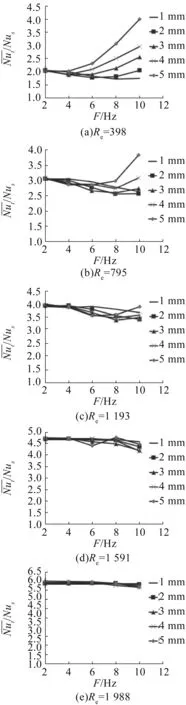
图6 Nut/Nus与振幅A的关系

图7为第二段不同雷诺数时不同振幅下随振动频率的变化。由于振动外力的作用，振动边界层中惯性力相对于粘性力的作用效果增强，流体边界层遭到破坏，换热强度得到提高。但因该段流体温度升高，流体与壁面温差减小，并且靠近边界层流体流速下降，整体换热强度有所下降，换热强度随着振动频率的增大而降低，Re越小，降低的越明显。Re=1 988时，振动产生的惯性力相对粘性力的作用效果趋于稳定，换热强度波动幅度在10%以内。

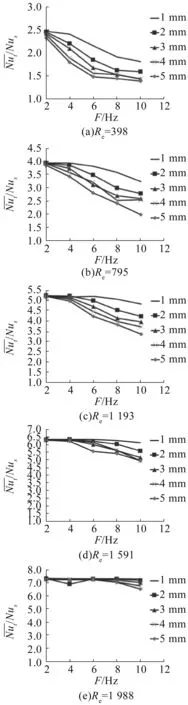
图7 Nut/Nus与振幅A的关系

图8为第三段不同雷诺数时不同振幅下随振动频率的变化。Re=398和Re=795时，换热强度随着振动频率的增大而提高，Re越小，提高越明显。Re=1 988时，振动边界层[13]流体受到的惯性力作用效果减弱，边界层破坏程度不再变化，换热强度也不再随着振动频率和振幅的变化而改变。

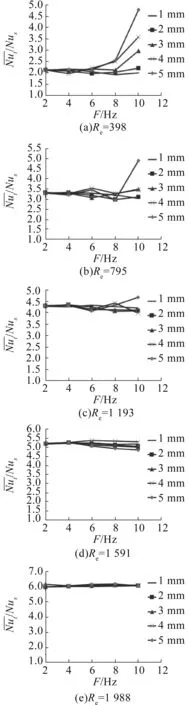
图8 Nut/Nus与振幅A的关系

图9为三段直管在Re=398，振幅为5 mm，振动频率为10 Hz下时相位270°的速度矢量图，三段直管内流体流速都因为振动而产生y方向的分速度。第一段和第三段管道靠近壁面处的流体依然有沿管道轴向的分速度，而第二段管道靠近上壁面处的流体流速有沿管道轴向与来流速度方向相反的分速度，造成该段换热强度减弱。

图9 Re=398 A=5 mm f=10 Hz速度矢量图

3 结语

(1) 振动可以强化振动圆管的传热，工况下传热强度最大可提高600%。

(2) 在相同频率和振幅的情况下，雷诺数越大，强化换热效果越好；在相同的振动条件下，雷诺数越小，强化效果改变越明显。

(3) 随着换热管道的加长，换热效果随着振动频率和振幅的增大，会在低频率和低振幅条件下的换热强度的基础上下降，最多下降18.3%。

参考文献：

[1] 胡海涛,张琳,黄文件,等.汽车换热器的分类和发展趋势[J].汽车工程师,2015(1):15-17.

HU Hiatao, ZHANG Lin, HUANG Wenjian, et al. Classification and Future Trends of Automotive Heat Exchanger[J]．Tianjin Auto，2015 (1)：15-17．

[2]ASHLEY,HOLT,HAVILAND,et al. Bending Vibrations of a Pipe Line Containing Flowing Fluid[C]// 2010:229-232.

[3]FEODOS EV VP. Vibrations and stability of a pipe when liquid flows through it [J]. Inzhenernyi Sbornik,1951(10):169-170.

[4]KLACZAK A. Report from experiments on heat transfer by forced vibrations of exchangers[J]. Heat and Mass Transfer, 1997, 32(6): 477-480.

[5]宿艳彩. 弹性管束流体诱导振动及换热特性研究[D]. 济南：山东大学, 2012.

[6]程宏伟, 杨学锋, 邓建新, 等. 管带式散热器翅片振动传热仿真研究[J]. 车用发动机, 2013, 13(5): 57-60.

CHENG Hongwei, YANG Xuefeng, DENG Jianxin, et al. Simulation Investigation on Louvered-fin Vibration Heat Transfer for Ribbon-tubular Radiator[J]．Vehicle Engine，2013，13(5)：57-60.

[7]吴艳阳, 刘利军, 喻九阳, 等. 振动圆管内对流传热特性及场协同分析[J]. 石油化工设备, 2011(6): 1-5.

WU Yanyang, LIU Lijun, YU Jiuyang, et al. Convective Heat Transfer Characteristics and Field Synergy Analysis Inside Vibration Circular Tube[J]. Petro-Chemical Equipment,2011(6):1-5.

[8]俞接成. 脉冲流动和壁面振动传热研究[D]. 北京：清华大学, 2005.

[9]于冲, 王旭, 董福安, 等. y+值对翼型气动参数计算精度的影响研究[J]. 空军工程大学学报(自然科学版), 2012, 13(3): 25-29.

YU Chong, WANG Xu, DONG Fuan, et al. The Study of Effect of y + on Precision of Pneumatic Parameters of Foil[J]． Journal of Air Force Engineering University(Natural Science Edition)，2012，13(3)：25-29．

[10]鲁红亮, 陶红歌, 胡云鹏, 等. 平行流换热器中热流体分布均匀性的研究进展[J]. 制冷学报, 2010, 31(6): 39-45.

LU Hongliang, TAO Hongge, HU Yunpeng, et al. State-of-the-art of Thermo-fluid Uniform Distribution in Microchannel Heat Exchanger[J].Journal of Refrigeration,2010,31(6).

[11]RADHAKRISHNAN S, PIOMELLI U. Large-eddy simulation of oscillating boundary layers:Model comparison and validation[J]. Journal of Geophysical Research Oceans, 2008(113): 394-394.