考虑距离因素的多方式交通超级网络均衡配流模型及算法
周豪,四兵锋,汪勤政
(北京交通大学交通运输学院,北京 100044)
经济的快速发展和城市化进程的不断推进,使得居民出行距离不断增加,供出行者选择的交通方式也越来越多。不同方式在不同距离范围内有着不同优势,例如,自行车适合较短距离出行,小汽车适合较长距离出行,而电动汽车因为受到电量约束,出行距离具有上限。因此,出行距离是影响出行者方式选择的重要因素。此外,随着出行距离的增加,出行者所花费的出行成本也会相应上升,因此,距离因素也会影响出行者的路径选择。在多方式交通系统中,出行者的选择行为会直接决定其出行活动,所有出行活动的聚集现象则形成了网络流量状态。因此,研究考虑距离因素的出行者选择行为及在此基础上的多方式交通配流问题对于现代综合交通管理具有重要的现实意义。
自Wardrop在1952年提出了“用户平衡条件”的概念,尤其是Beckmann在1956年提出与之等价的数学模型后,基于用户平衡思想的交通配流理论得到了快速发展。然而,大部分研究是针对单一模式的交通网络展开的。例如,城市公交网络客流分配[1]、城市轨道交通网络客流分配[2]等。目前,有些学者开始关注多方式交通网络的配流问题,例如,Wu等[3]考虑了步行和公交两种方式,建立了一个分层网络模型,并提出了多方式网络平衡配流模型;黄海军等[4]研究了组合出行方式下的混合均衡分配问题,提出了与用户均衡条件等价的变分不等式模型;四兵锋等[5]提出了一种分层网络结构来描述多方式交通网络,并提出了考虑不同方式之间相互干扰的变分不等式模型;汪勤政等[6]构建了多方式交通系统的可换乘超网络模型,考虑出行者的出行规律、出行行为和换乘等条件,基于图的遍历算法和Dijkstra算法,提出了超网络有效超路径的搜索算法和最短有效超路径算法。近年来,随着电动汽车等新能源交通工具的发展,有些学者开始关注考虑路径约束的网络配流问题。例如,Kang等[7]采用基于活动的方法,对出行者的充电路径选择进行了研究;He等[8]考虑了电动汽车单一模式交通网络,提出了基于出行距离约束下的用户平衡配流模型。然而,在该研究中,所建立的广义费用函数均没有考虑距离因素对出行者选择行为的影响,路径约束条件只是针对电动汽车单一模式,没有考虑多方式组合出行条件下距离因素对出行行为的影响。
在以往的研究中没有考虑出行距离对出行者广义费用和出行选择的影响,且只考虑对单一方式进行路径约束,没有综合考虑出行者在整个多方式交通系统中的出行选择行为。本文针对多方式交通网络的流量分配问题展开研究,综合考虑距离因素对出行者的方式选择和路径选择,特别深入分析了距离因素对出行者广义感知费用的影响,定义了超路径,提出了最短超路径搜索算法。并提出了考虑距离因素的多方式交通网络均衡流量分配模型及算法。最后,通过一个简单算例对模型及算法进行了验证分析。
1 多方式交通超级网络模型
在多方式交通网络中,出行者完成一次出行往往需要经历4个阶段:从出行起点行走或行驶到达某一网络节点,即上网过程;采用某种交通方式行驶到达换乘节点,即运行过程;在换乘节点从一种交通方式步行换乘到另一种交通方式,即换乘过程;从目的网络节点行走或行驶到达最终的出行终点,即下网过程。根据出行者的出行特征,本文采用超网络结构来描述多方式交通系统。在多方式超级交通网络中,每种交通方式都有自己的运行子网,不同交通子网之间通过换乘节点进行连接。多方式超级交通网络可描述为:
G=(M,V,A),
(1)
其中,G表示多方式超级网络;M表示交通方式集合;V表示交通节点集合;A表示各类弧的集合。
在多方式超级网络中,根据节点和弧的不同属性,可将其分为不同的类别,不同类别的节点和弧可通过不同的状态向量进行描述。节点可分为出行端点和非出行端点,出行端点表示一次出行的起点或终点,这类节点集合用V1来表示,其中的元素用单变量r或s表示,即r,s∈V1;而非出行端点表示出行过程中的中间节点,这类节点集合用V2来表示,其中的元素用二维向量(m,v)表示,即(m,v)∈V2,m和v分别表示节点的交通方式属性和位置属性。在多方式超级网络中,弧可以分为上网弧、运行弧、换乘弧和下网弧等四类,不同类型的弧的集合分别用A1、A2、A3、A4表示,即:
A=A1∪A2∪A3∪A4,
(2)
可用所连接的两个相邻节点来表示一条弧,例如上网弧可表示为{r,(m,v)},运行弧可表示为{(m,v1),(m,v2)},换乘弧可表示为{(m1,v),(m2,v)},而下网弧可表示为{(m,v),s}。
在多方式超级网络中,出行者从起点到终点完成一次出行,需要经历上网、乘车、换乘、下网等一系列出行活动,这些活动可通过超网中具有序列关系的点或弧进行描述。
在此,本文提出超路径的概念来描述出行过程,定义:超路径是指在多方式超级网络中由起点到终点有连接关系的多方式交通网络节点所组成的序列。例如,从起点r到终点s的一条超路径可表示为:
r→(m1,v1)→(m1,v2)→…→(m1,vn)→(m2,vn)→…→(mn,vw)→s
(3)
在实际出行中,出行者不会考虑起点到终点之间所有连通的超路径,因此,需要对超路径进行限定,本文将满足下述条件的超路径定义为有效超路径,并假定出行者进行出行选择时仅考虑有效超路径,将r-s之间的有效超路径所组成的集合记为Krs:
(1)换乘次数不超过一个给定的最大值nmax;
(2)不存在连续换乘弧;
(3)不包含回路;
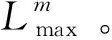
在一条有效超路径中,通常会包括多段连续运行弧,也就是说,出行者在进行换乘之前,会在某一种交通子网中出行一段距离,然后在适当的换乘点转换到另外一种交通子网中。本文定义子路径为:在多方式超级网络的一条有效超路径中,相邻的上网弧、换乘弧和下网弧之间的运行弧序列。显然,有效超级路径可以看成是由上网弧、子路径、换乘弧以及下网弧所组成的。例如,在式(3)表示的超路径中,以下节点序列则构成了该超路径的一条子路径。
(m1,v1)→(m1,v2)→…→(m1,vn)。
(4)
图1给出了一个简单的多方式超级网络,在这个超网中包含4个子网,分别为小汽车子网(c)、电动车子网(e)、自行车子网(b)和公交车子网(p)。

图1 多方式超级网络Fig 1 The multimodal super network
图1中,r→(b,1)→(b,2)→(p,2)→(p,5)→(p,8)→(p,9)→s就是该超网络中的一条有效超路径,该有效超路径中包含了自行车和公交两种方式的子路径。(p,2)→(p,5)→(p,8)→(p,9)是其中的一条公交车子路径。
2 考虑距离因素的出行广义费用
在多方式交通网络中,出行者在出行中既要选择交通工具,还要选择出行线路,影响出行者选择的因素有很多,包括时间、花费、换乘、舒适度等。在以前的研究中,很少考虑距离因素对出行者交通选择的影响,然而,距离因素是影响出行者交通选择,尤其是方式选择的重要因素。例如,随着距离的增加,出行花费会增加,舒适度会下降,且不同方式对于距离的敏感性也是不同的。
根据以上分析,出行者的出行过程包括上网、车辆运行、换乘及下网4个过程。相应的,出行者在这些过程中所承担的费用可用这些弧段上的费用来表示。超路径费用由上网费用、子路径费用、换乘费用和下网费用组成,其中上网费用、换乘费用和下网费用均为常数,是对时间费用的适当放大;而子路径费用可以由运行弧费用求得。
首先,构建上、下网弧以及换乘弧的广义费用。而子路径费用可以由运行弧费用求得,包括时间费用和价格费用。其中,时间广义费用通过对子路径的运行时间适当放大得到,放大因素包括道路拥挤、公交车车内拥挤以及距离增加带来的舒适度损耗成本;而子路径的价格费用则是距离的单调递增函数。
根据以上分析,对各弧段的广义费用进行分析和建模。
(1)上网弧和下网弧的广义费用
上网弧费用是指出行者从出行起点到达相邻网络节点所花费的时间,而下网弧费用则表示出行者从最后的网络节点到出行终点所花费的时间。通常,这两类弧上的费用可以假定为常数,即:
(5)
(6)
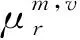
(2)换乘弧广义费用
换乘弧的费用是指换乘时间,由步行时间和等待时间组成,本文假定换乘时间为常数。由于换乘通常需要消耗体力,因此,换乘时间所产生的出行者心理感知费用是对换乘时间的适度放大。节点(m1,v)到(m2,v)间的换乘费用可表示为:
(7)
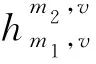
(3)子路径广义费用
根据前面的定义,子路径是由同一方式的运行弧组成的,子路径上的费用表示出行者在某一方式子网内出行一段距离所承担的费用。通常,影响出行者出行选择的因素包括时间、价格、舒适度等,其中时间因素就是车辆的行驶时间,价格因素包括票价、油耗等,而舒适度则是指车辆内部拥挤所产生的心理费用。在实际的出行过程中,价格因素和舒适度因素均和车辆行驶距离有关,例如,交通价格(或者油耗)一般会随着距离的增加而增加,而车内的舒适度会随着出行距离的增加而下降,并且不同方式的广义费用随距离变化的趋势也是不同的。
首先,在多方式超级网络中,方式m的车辆在运行弧上的行驶时间可表示为路段流量的单调增函数,如果考虑不同方式车辆之间的相互干扰,可采用式(8)所示的函数形式进行计算[9]:
(8)
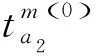
由于不同方式车辆的平均载客人数不同,因此,选择不同交通方式的出行需求所形成的道路流量是不同的,可采用下式计算不同方式车辆的道路流量[9]:
(9)
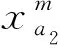
此外,出行者乘坐车辆行驶过程中,除了出行时间的之外,还需要承担由车内拥挤所带来的舒适性成本,尤其对于公交出行而言。因此,将方式m的出行时间放大,表示舒适度对于出行的影响,如式(10)所示。
(10)

同时,随着出行距离的增加,由时间和舒适度所产生的费用会逐渐放大,并且不同交通方式对距离的敏感性是不同的。因此,某一超路径k上子路径lk上的出行时间和舒适度成本如式(11)所示。
(11)
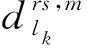
(12)
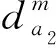
(13)
其中,am和bm表示与不同方式相关的待定参数。
在子路径费用中,除了时间和舒适度的心理感知费用外,影响出行者交通行为的因素还有价格因素。对于小汽车来说,这部分费用包括油耗、过路费等,对于公交而言,则为票价。通常,价格费用与出行距离直接相关,距离越长,所花费价格越高。可以用式(14)来表示OD对r-s之间方式为m的有效超路径k上子路径lk的价格费用:
(14)
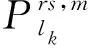
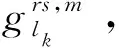
(15)
式中,τ为待定参数。
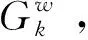
(16)
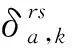
(17)
以路段流量为变量,超路径的广义费用可表示成如下形式:
(18)
3 多方式交通网络均衡配流模型
本文采用用户平衡(user equilibrium,UE)准则对网络中的流量进行分配,该准则也被称为Wardrop平衡原则。当交通网络的流量分配达到平衡时,在OD对r-s之间的所有有效超路径中,出行者所采用的各条路径上的广义费用均相等,且不大于未被使用路径上的出行费用。其费用和流量有如下关系:
(19)
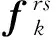
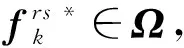
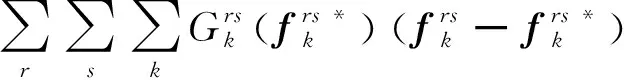
(20)
其中:

r,s∈V1,k∈Krs,a∈A,m∈M}。
(21)
4 求解算法
本文采用连续平均算法(MSA算法)求解该UE平衡配流问题[10],具体步骤如下:

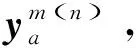
Step4:迭代更新,计算:
(22)
Step5:收敛性检查。如果满足
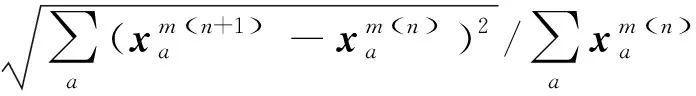
(23)
算法结束;否则,令n=n+1,转Step2。
在求解本文的UE问题时,需要确定最短有效超路径,传统的最短路径搜索算法对本文所考虑的子路径问题无法描述,因此本文基于Dijkstra算法,提出考虑子路径的超网络最短有效超路径搜索算法,具体步骤如下:

Step2:取Ci中的某一节点,如j:
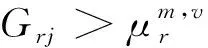
(2)若弧(i,j)∈A2,判断:
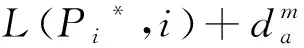
b)若弧m(i,j)=0,转Step3;
(3)若(i,j)∈A3,判断弧(pi,i)∈A3是否成立,是,则转step6;否,转Step4;
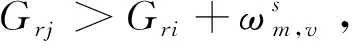
Step4:令n(r,j)=n(r,i)+1,判断n(r,j)⦤nmax是否成立,是,转step5;否,则转Step6;
Step6: 将j从集合Ci中移除, 判断Ci是否为空,是,转入Step7;否,转入Step2;
Step7:找出标号为0的点中费用最小的点,如j,令s(j)=1,并将j设为当前节点,令K=K+1,转Step8;
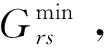
5 算例分析
以图1所示的多模式交通网络为例对说明模型及算法进行验证,对文中参数作如下取值:
(1)η=1.1,ε=0.001,τ=0.2;
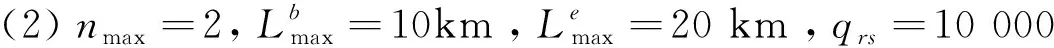
各交通方式相关信息如表1~表3所示:
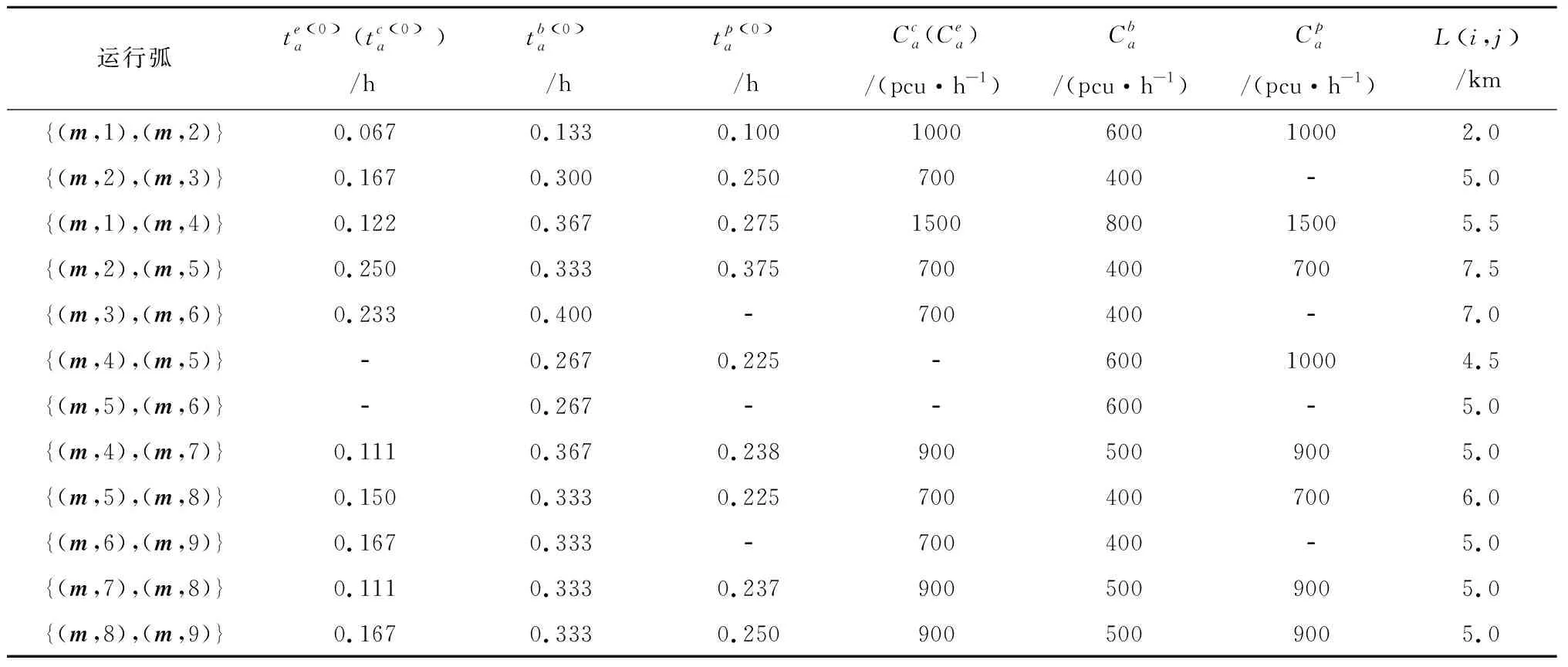
表1 弧段的相关信息
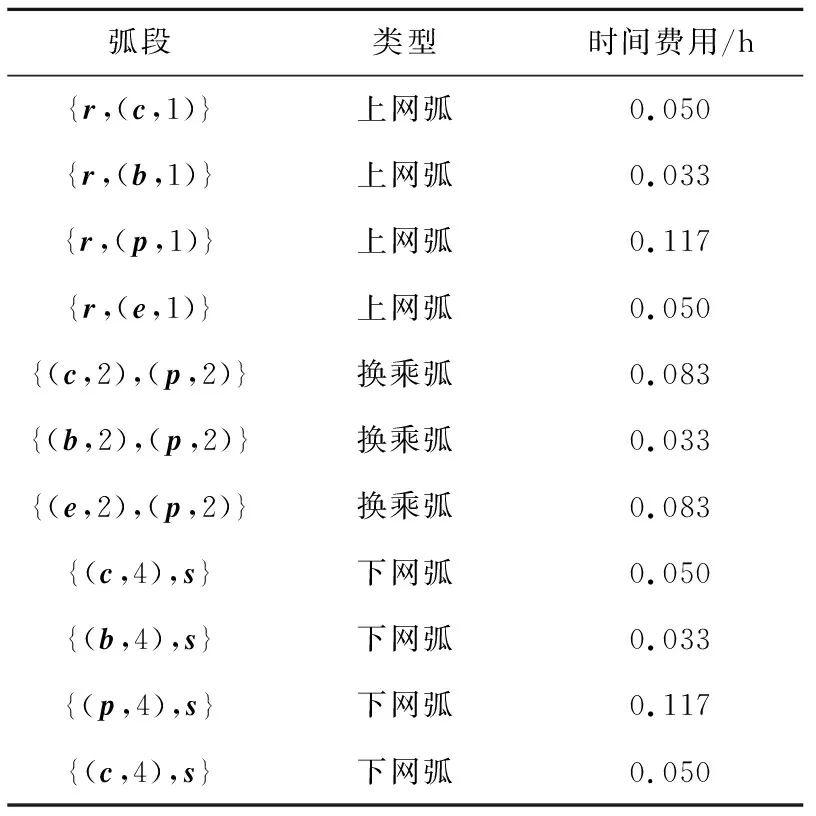
表2 上、下网弧及换乘弧相关数据
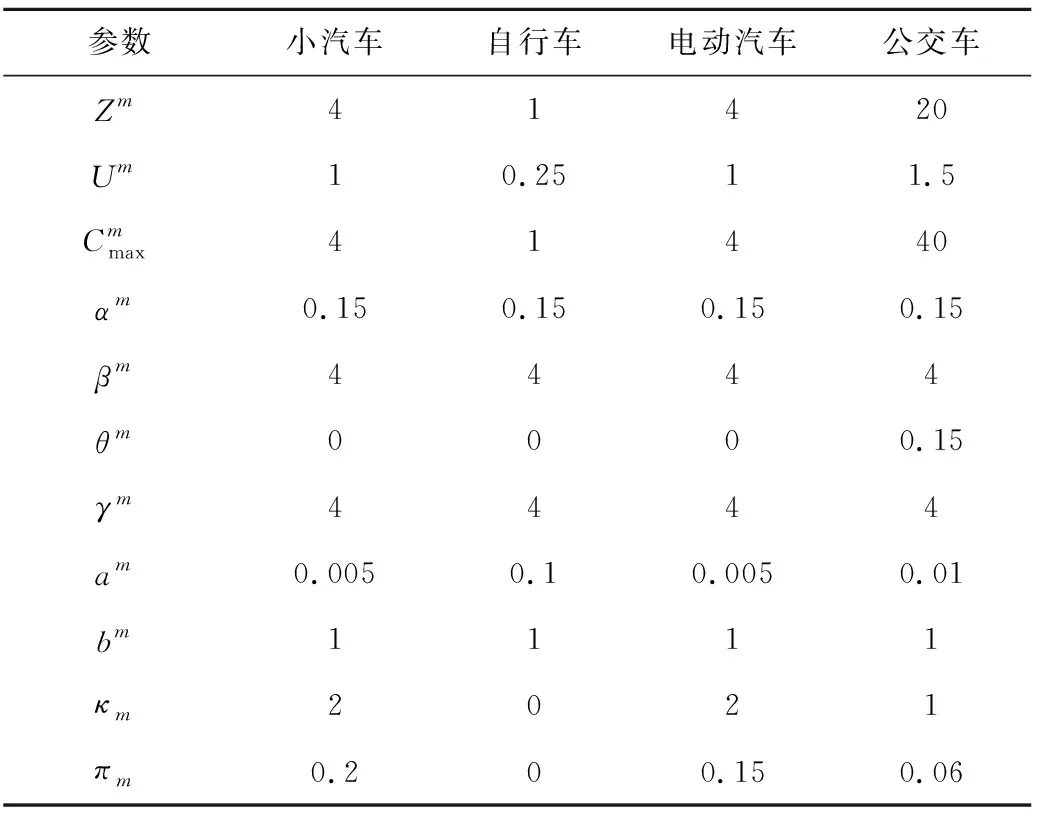
表3 交通模式的相关数据
首先分析MSA算法的收敛性,通过每次迭代中弧段{(c,1),(c,2)} 上小汽车和{(e,1),(e,2)}上电动汽车出行需求的变化来表示算法的收敛性。图2给出了MSA算法的前30次的计算结果。可以看出,MSA算法具有明显的收敛性质。

图2 交通需求随迭代次数的变化Fig.2 Variations of demands of car and electric car vs iteration times
用MATLAB对算例进行求解,首先对网络中的参数赋值,求得各弧段以及子路径的费用,用第4部分中的最短超路径搜索算法寻找最短路径。对最短路径采用全有全无配流,得到附加交通流,并更新各弧段的流量。重复以上过程,直至达到网络平衡的收敛条件。本文中的简单算例,共有18条超路径,经程序计算,当网络达到平衡状态时,超网络中的有效超路径一共有5条,每条路径的出行模式如表4所示。当达到平衡状态时,根据本文算法得到的各弧段上的交通需求如图3所示。

表4 有效超路径分配结果
从图3的配流结果中可以看出,在有电动汽车行驶的路段上(例如路段{(m,2),(m,3)}),小汽车的流量均为0,这是因为相同路径上电动汽车的广义费用比小汽车低,因此出行者会全部选择电动汽车。但是当路径的距离超出电量限制时,例如超路径r-(e,1)-(e,4)-(e,7)- (e,8)-(e,9)-s,出行者便不能选择电动车出行。自行车流量只分布在路段{(b,1),(b,2)}上,其他路段上自行车的流量为0。这是因为自行车只适宜在较短的距离内出行,当距离较长时,自行车将消耗较大的人力,出行者便不会选择,为了发挥自行车短距离出行的优势,自行车通常在多方式组合出行中采用。选择单模式的出行量占90.75%,选择多方式组合的出行量占9.25%,这是因为多方式换乘的费用较高,导致出行广义费用增加,因此选择多方式组合出行的流量较少。
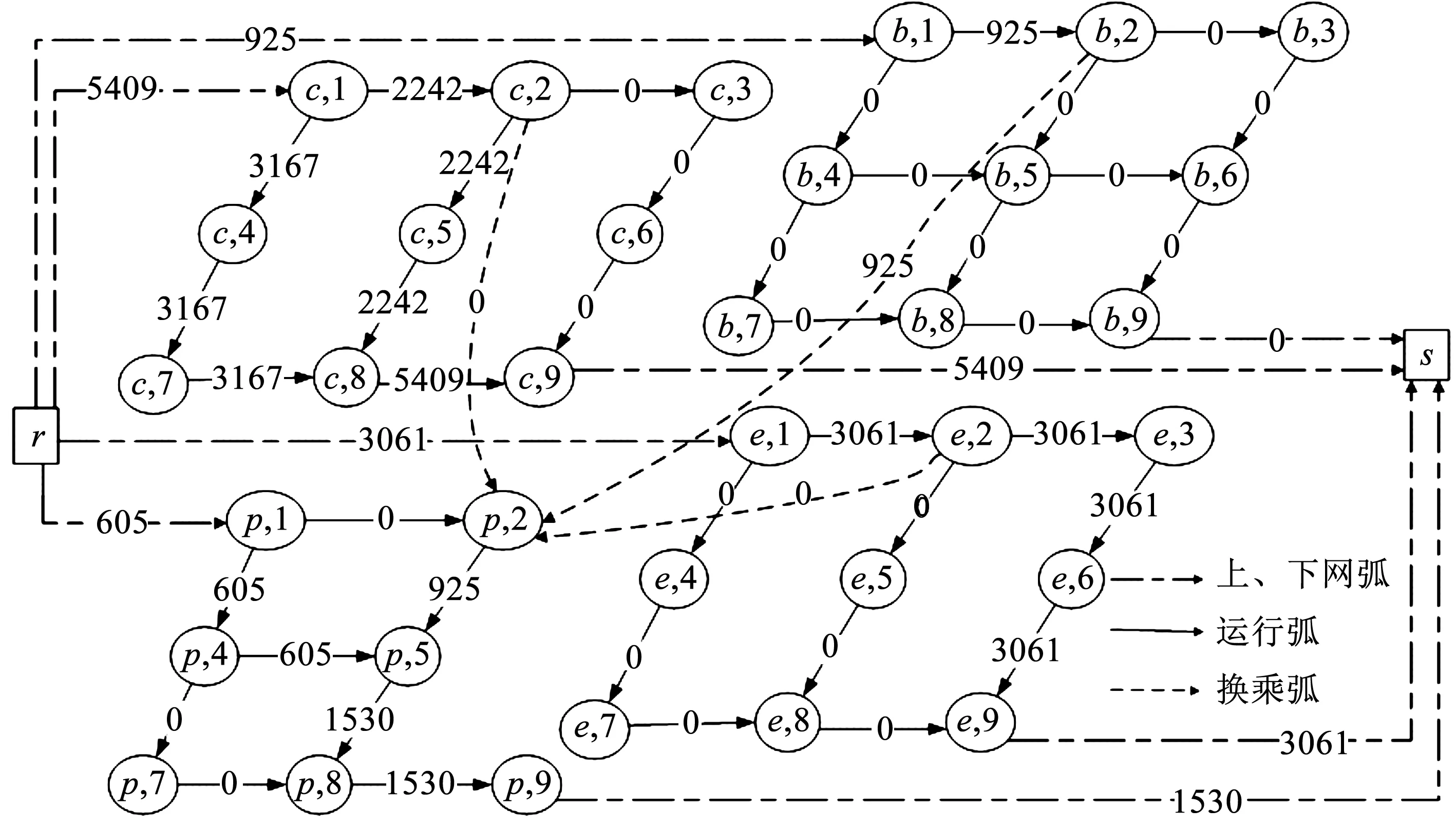
图3 平衡时超网络的路段流量Fig 3 The link flow of super network at equilibrium
6 结语
本文基于图论方法建立了用于描述多方式组合出行的超网络模型,验证结果表明本文提出的模型和算法是有效的,并且说明了距离是影响出行者方式选择和路径选择的重要因素。距离既影响时间,又影响价格,无论是对出行者的路径选择或方式选择都有着重要的影响,考虑距离因素更符合出行者的实际出行选择。通过算例说明了距离对出行选择的影响,例如出行者仅在短距离出行中会选择自行车,而长距离中选择其他交通工具,这一结果是与实际相符的。
参考文献:
[1]杨新苗, 马文腾. 基于GIS的公交乘客出行路径选择模型[J]. 东南大学学报(自然科学版), 2000, 30(6):87-91.
[2]SI B F, ZHONG M, LIU J F, et al. Development of a transfer-cost-based logit assignment model for the Beijing rail transit network using automated fare collection data[J]. Journal of Advanced Transportation, 2013; 47(3):297-318.
[3]WU Z, LAM W. A network equilibrium model for congested multi-mode transport network with elastic demand[C]// Proc. 7th Conf. Hong Kong Society for Transportation Studies,Hong Kong,2002:274-283.
[4]黄海军, 李志纯. 组合出行方式下的混合均衡分配模型及求解算法[J]. 系统科学与数学, 2006, 26(3):352-361.
[5]四兵锋, 杨小宝, 高亮,等. 基于出行需求的城市多模式交通配流模型[J]. 中国公路学报, 2010, 23(6):85-91.
[6]汪勤政, 四兵锋. 换乘约束下城市多方式交通分配模型与算法[J]. 交通运输系统工程与信息, 2017, 17(4):159-165.
[7]KANG J, RECKER W. An activity-based assessment of the potential impacts of plug-in hybrid electric vehicles on energy and emissions using 1-day travel data[J]. Transportation Research Part D Transport & Environment, 2009, 14(8):541-556.
[8]HE F, YIN Y, LAWPHONGPANICH S. Network equilibrium models with battery electric vehicles[J]. Transportation Research Part B Methodological, 2014, 67(3):306-319.
[9]四兵锋,钟鸣,高自友.城市混合交通条件下路段阻抗函数的研究[J]. 交通运输系统工程与信息, 2008, 8(1):68-73.
[10]四兵锋,高自友.交通运输网络流量分析与优化建模[M]. 北京:人民交通出版社, 2013.

