太阳花散热器的热性能分析

贾磊，季璨，江亚柯，刘志刚

(齐鲁工业大学(山东省科学院)，山东省科学院能源研究所，山东 济南 250014)

太阳花散热器(图1)多采用铝合金通过挤压成型工艺加工，因铝合金导热系数高、密度小，用其加工的太阳花散热器散热性能良好、重量轻，因此在电子产品散热、LED照明等行业有着广泛的应用。

国内外学者深入地研究了太阳花散热器的热性能，对翅片数量、长度、高度及厚度等因素对散热性能的影响进行了数值研究。周建辉等[1-2]对强制对流的太阳花CPU散热器进行了研究，发现随着翅片数增加，翅片换热量增强，CPU温度降低，但翅片数增加到一定数量后,换热量提高缓慢，且会随着翅片增多，风阻增大而导致气流量减小，散热发生恶化。李艳红等[3]研究了风速对太阳花CPU散热器的影响，结果表明风速越大，芯片表面温度越低；在加热功率为125 W的条件下，风速增大到1.4 m/s以后，再增大风速对降温效果不再明显。张远波[4]研究表明对采用强制对流的太阳花CPU散热器，芯片温度随着散热器长度的增加先降低后升高；研究还表明长度为0.05 m、外径为0.04 m且翅片数量为60时，其散热能力最强。

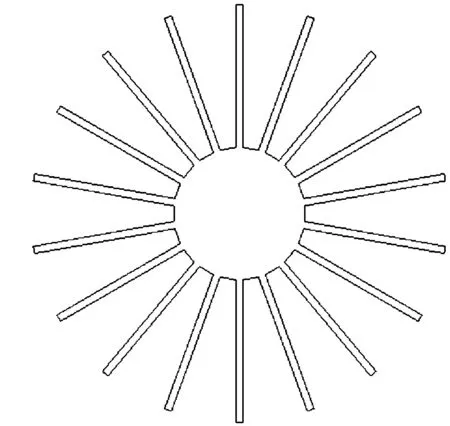
图1 散热器横截面Fig.1 Cross section of a sunflower radiator

针对热源置于散热器端部的太阳花散热器的热性能，国内部分学者对其进行了研究。李灏等[5]对太阳花散热器进行了结构优化，在基本保持重量不变的情况下，最高温度从75 ℃降低到了64 ℃。褚旭昭等[6]研究显示，翅片从30片增加到40片，最高温度由64.5 ℃降低到了62.6 ℃。向建化等[7]研究发现，结构参数对散热影响从大到小的顺序为翅片厚度、翅片数量、翅片高度及内孔直径。李中等[8]研究表明，对于外径为80.2 mm、内径为48.4 mm太阳花散热器，最佳翅片数量为26片。

综上所述，针对热源置于散热器中心且采用自然对流的太阳花散热器的热性能目前研究较少。在强制对流下的热性能和自热对流下的热性能不同，此外，热源布置在不同位置导致热量在散热器内的传导路径亦不同，其散热性能也不相同。鉴于此，本文将对热源置于散热器中心且以自然对流换热方式的太阳花散热器的热性能进行数值研究，并以实验相佐证，以系统阐释其传热机理。

1 模拟模型

控制性方程[9]为连续性方程：

。

(1)

动量方程：

(2)

(3)

。

(4)

能量方程：

(5)

其中，ρ为密度；u、v、w为速度在x、y、z方向的分量；Fx、Fy、Fz为体积力在x、y、z方向的分量；P为压力；μ为动力粘度；T为温度；Cp为定压比热。

计算区域如图2所示，在重力反方向的自由空间为200 mm，在重力下方自由空间为100 mm，在四周的自由空间为50 mm。计算区域的6个壁面设置为opening边界。密度模型采用理想气体模型，辐射模型采用DO(离散坐标辐射)模型，湍流选取零方程模型。散热器设置为铝合金材质，导热系数为205 W/(m·℃)，辐射发射率设置为0.18。空气温度为20 ℃。

因散热器外形复杂，不易在Icepak中直接建模，采用三维软件SolidEdge建模后再导入Icepak中。Icepak可以通过设置assembly的方式划分非连续网格，将散热器建立一个assembly，在其内部进行网格加密，外部空间则采用相对稀疏的网格，横截面的网格图见图3。

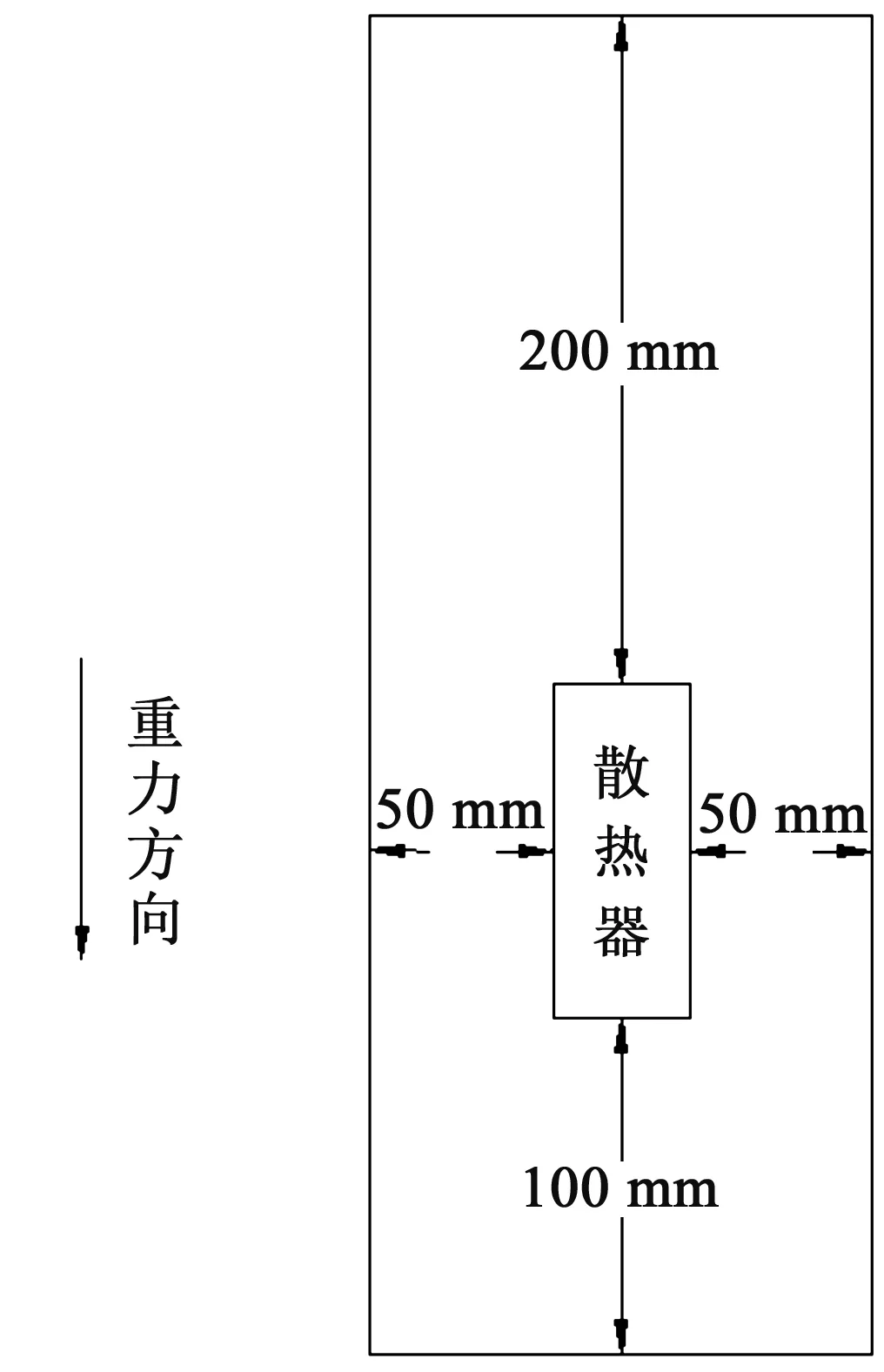
图2 计算区域Fig 2 Numerical simulation area

图3 网格划分图Fig 3 Numerical simulation grid

本文计算及实验所用太阳花散热器的参数如表1所示。

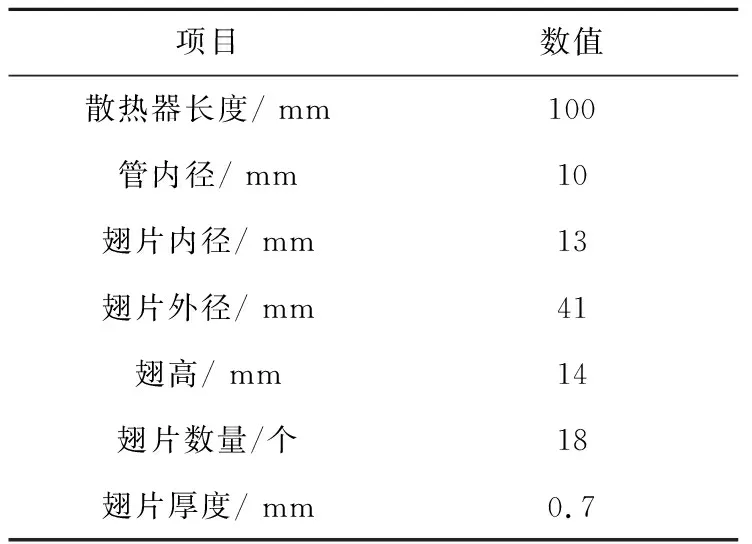
表1 太阳花散热器尺寸参数

2 实验验证

为了验证采用的模型是否合理，通过实验对数值模拟进行了验证，太阳花散热器的结构参数如表1所示，实验系统如图4所示。

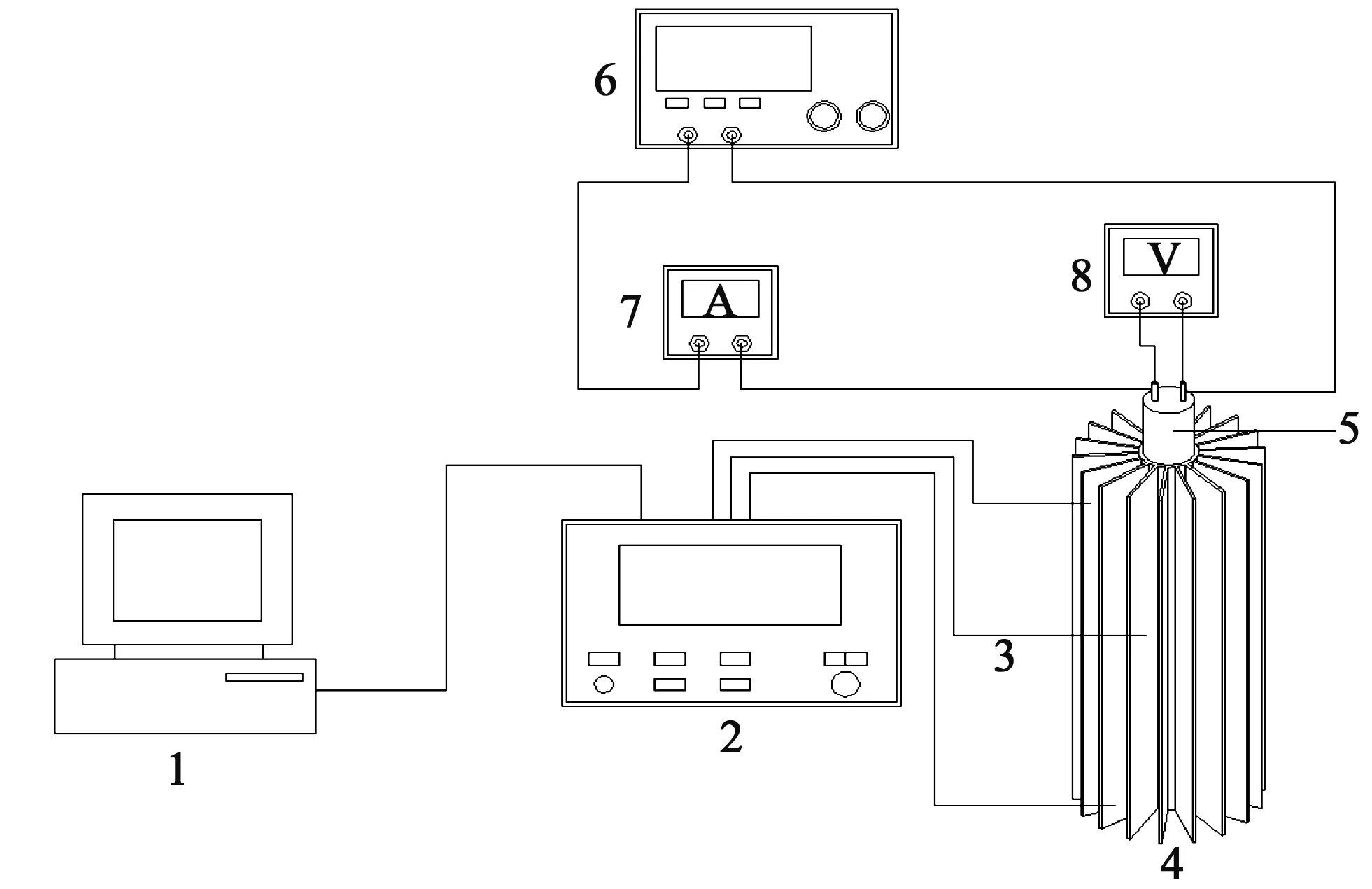
1计算机；2数据采集仪；3热电偶；4太阳花散热器；5电加热棒；6可调直流电源；7电流表；8电压表。图4 实验系统图Fig.4 Experiment system

散热器竖直布置于开放空间中，没有物体阻碍其周围气流的流动。电加热棒嵌入散热器管中，其直径和高度与散热器一致。电加热棒采用直流可调电源供电，电热棒两端的电压和电流分别用电压表和电流表测量。

在散热器长度方向均匀布置了5个热电偶，取其平均温度作为翅片的温度。采用2个热电偶测量环境温度，取其平均温度作为环境温度，测试期间环境温度基本保持在23 ℃。温度测量采用自制K型热电偶(Omega)，并用数据采集仪采集(Agilent 34972A)。

实验和模拟结果中翅片温度的对比如图5所示

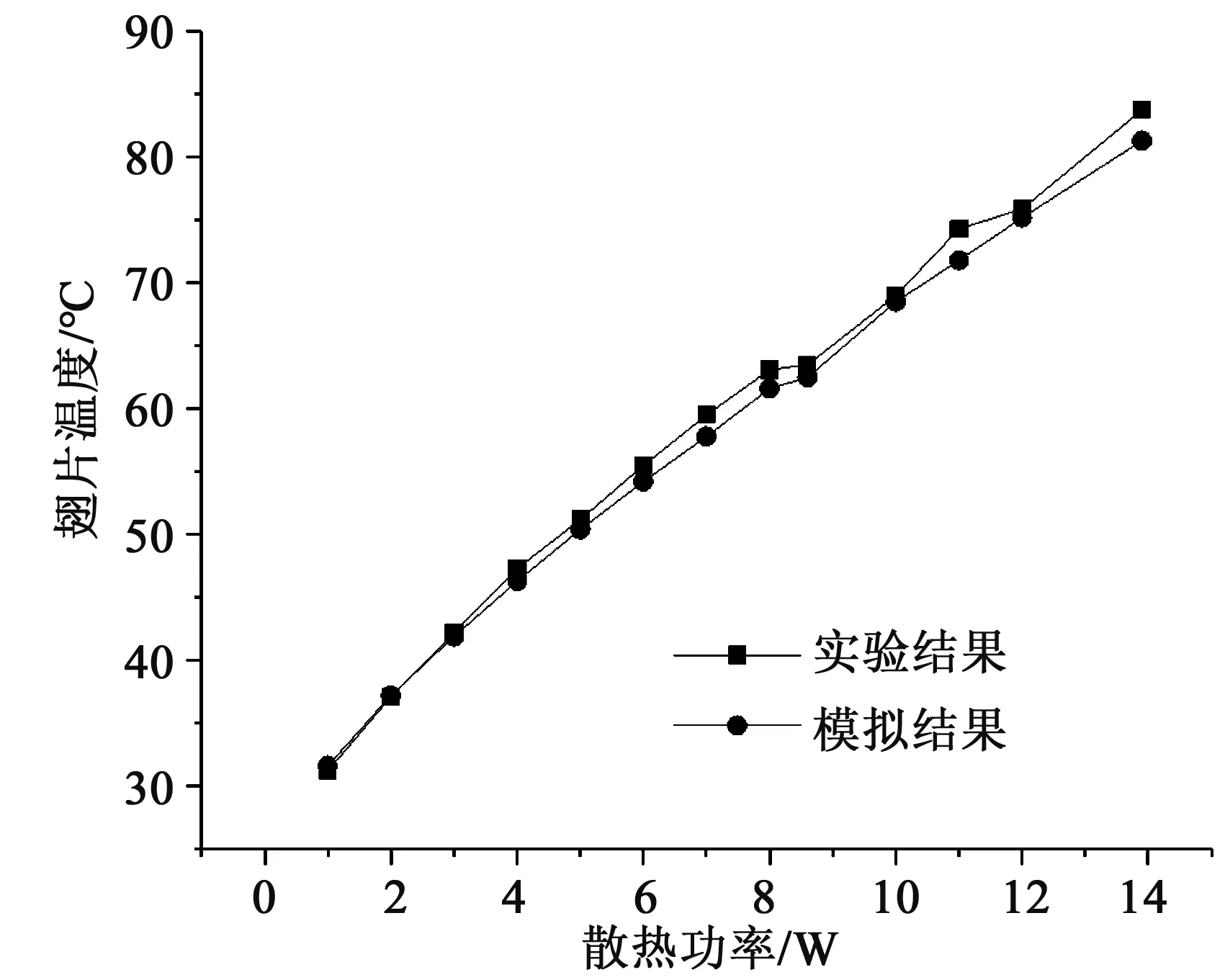
图5 实验与模拟结果对比Fig.5 Comparison of experiment and simulation results

由图5可知，在不同的散热功率下，实验和模拟结果中翅片温度基本一致，两者差距在3.5%以内，这表明数值模拟选用的模型和方法非常合理，模拟结果可靠。

3 模拟结果分析

3.1 翅片数量对热性能的影响

保持其他结构参数和功率不变，翅片温度和传热系数随着翅片数量变化趋势如图6所示。

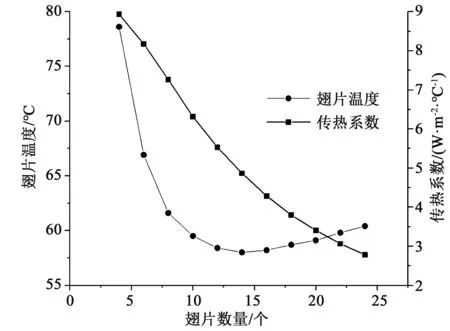
图6 翅片温度及传热系数与翅片数量的关系Fig.6 Varieties of fin temperature and heat transfer coefficient with fin number

由图6可知，翅片温度随着翅片数量的增多而先降低后升高，在翅片数量为14时翅片温度最低。翅片数量增量，其散热面积也线性增加；但翅片数量增加阻隔气体流动，因而会降低其传热系数。

不同翅片数量下翅片周围的温度场如图7所示。

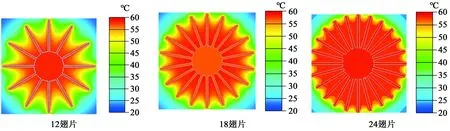
(1/2散热器长度处横截面)图7 不同翅片数量下翅片周围的温度场Fig.7 Temperature field around the fins under different fin numbers

由图7可知，随着翅片数量的增多，翅片周围空气的温度梯度逐渐降低，温度场和速度场密切相关，翅间空气的最大速度及空气流量与翅片数量的关系如图8所示。

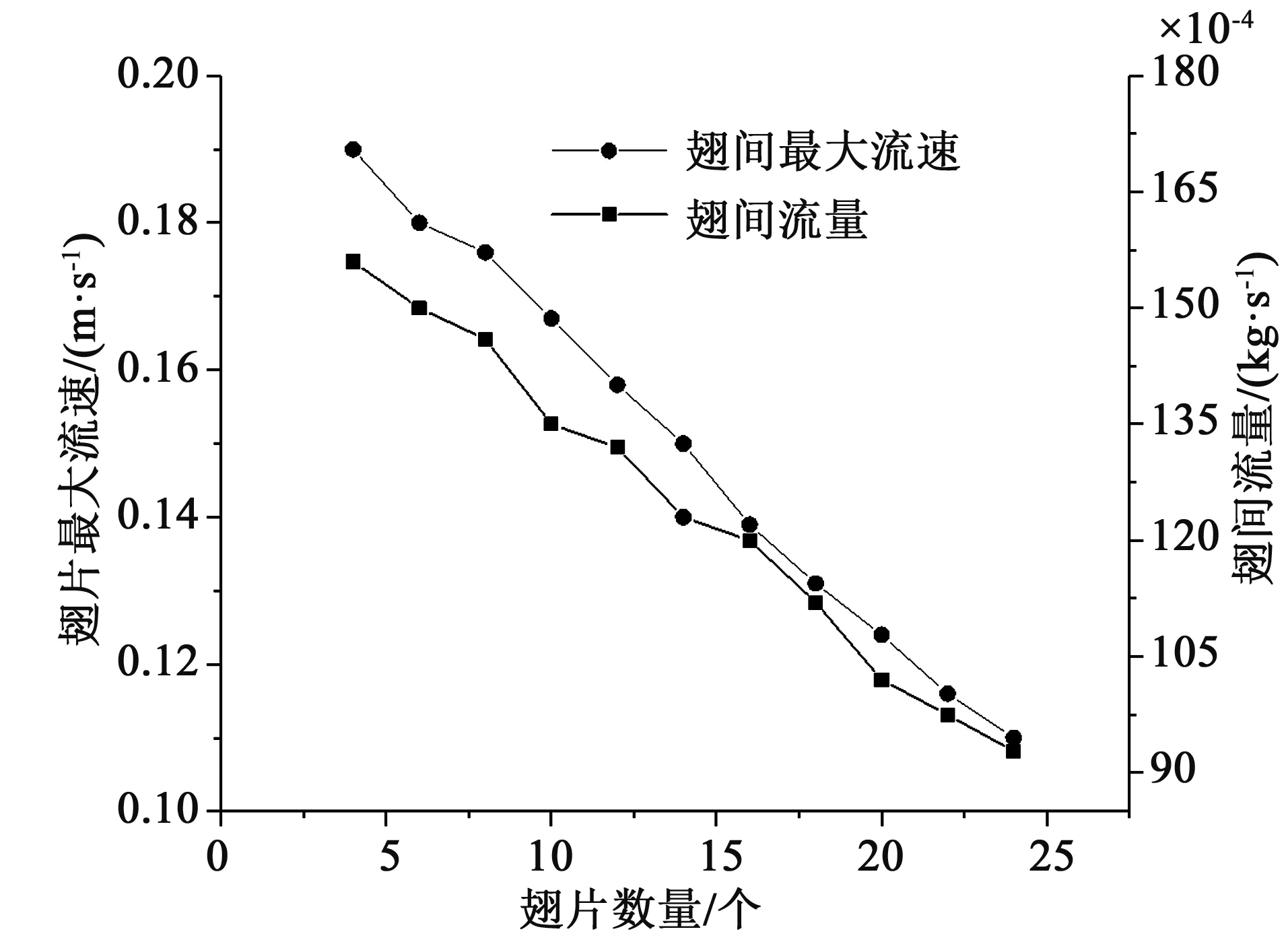
图8 翅间最大流速及翅间流量与翅片数量的关系Fig.8 Varieties of maximum velocity and flow rate with fin number

由图8可知，随着翅片数量的增多，翅片间的气流速度和气流量都在在降低，而翅片散热量和冷空气的温度是不变的，因此空气吸热后温度更高，导致空气与翅片间的温度梯度减小，进而使得对流传热系数降低。

3.2 散热器长度对热性能的影响

保持其他结构参数和功率不变，翅片温度及传热系数随着散热器长度变化趋势如图9所示。

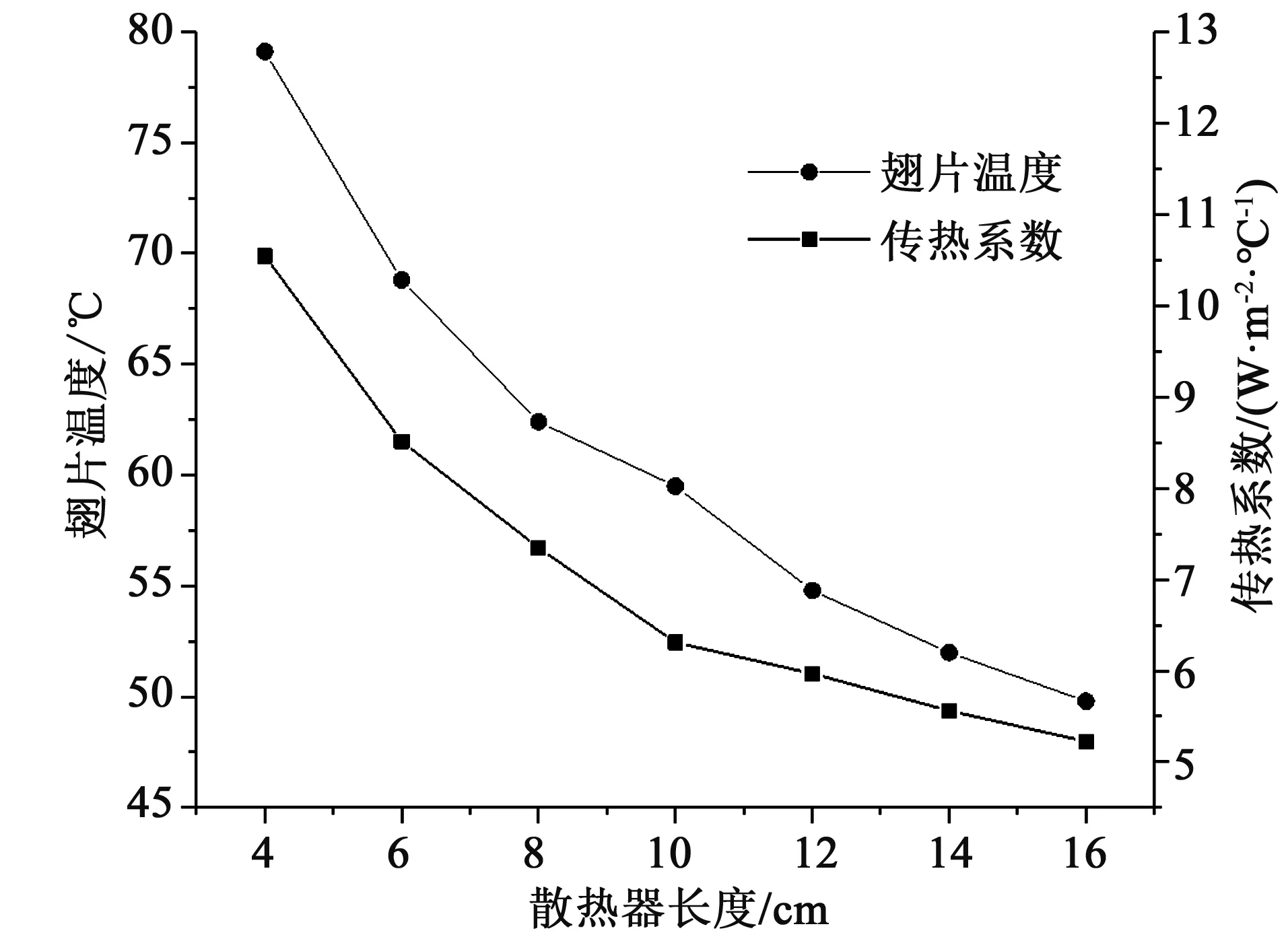
图9 翅片温度及传热系数与散热器长度的关系Fig.9 Varieties of fin temperature and heat transfer coefficient with radiator length

由图9可知，随着散热器长度的增加，翅片温度在逐渐降低，但是温度降低的幅度在减缓。随着散热器长度的增加，散热面积也在增加，而传热系数则随着散热器的长度的增加而减小，这是因为翅片周围空气的温度梯度随着散热器长度增加而逐渐降低(图10)。

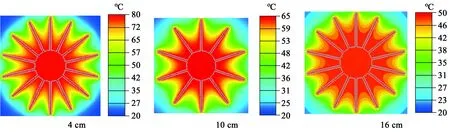
(1/2散热器长度处横截面)图10 不同散热器长度下翅片周围的温度场Fig.10 Temperature field around the fins under different radiator length

图10对比了散热器长度为4 cm、10 cm、16 cm时散热器周围的温度场，随着散热器长度的增加，翅片周围空气的温度梯度明显降低，导致传热系数随着散热器的长度的增加而减小。

3.3 翅片高度对热性能的影响

保持其他结构参数和功率不变，翅片温度和传热系数与翅片高度的关系如图11所示。

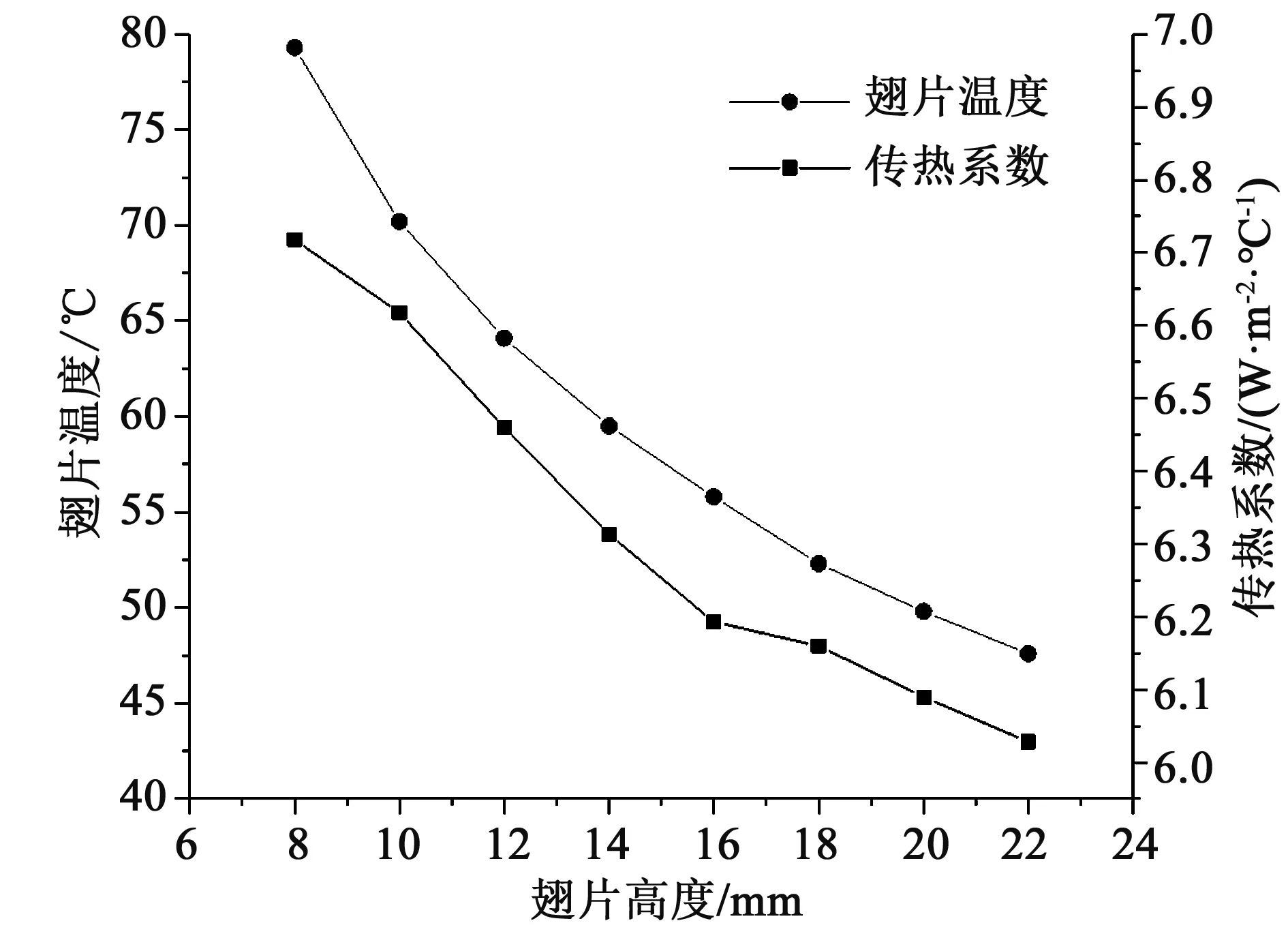
图11 翅片温度及传热系数与翅片高度的关系Fig.11 Varieties of fin temperature and heat transfer coefficient with fin height

由图11可知，随着翅片高度的增加，翅片温度在逐渐降低。随着翅片高度的增加，散热面积在随之增加，而传热系数则随着翅片高度的增加逐渐降低。自然对流的驱动力是空气密度差产生的浮升力，密度差由空气温差导致，空气温差越小，浮升力越小。随着翅片高度增加，浮升力随着空气温差降低而减小，自然对流减弱，传热系数随之降低。

翅片高度越大，从翅根到翅顶的热阻就越大，翅顶温度越低，翅片散热效果就越差。翅片的散热效果可以用肋效率η表示，肋效率的定义为实际散热量与假设整个肋片表面处于肋基温度下散热量的比值[10]。

对于本文研究的翅片，其肋效率计算公式[10]为

(6)

(7)

其中，H为翅片高度；h为对流传热系数；λ为翅片材料导热系数；δ为翅片厚度。

据此计算的翅片在不同高度下的肋效率如图12所示。

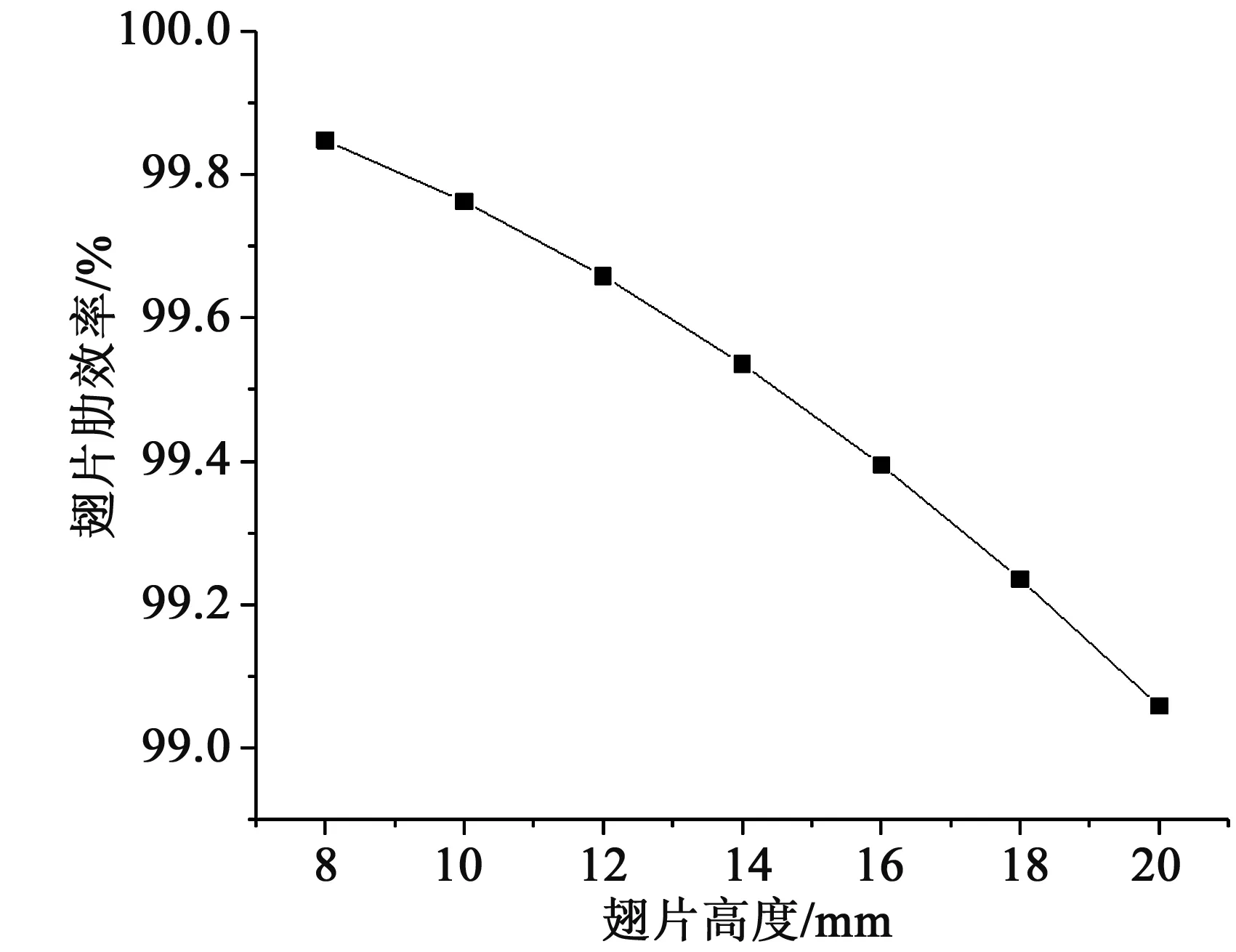
图12 翅片肋效率与翅片高度的关系Fig.12 Varieties of fin efficiency with fin height

由图12可知随着翅高的增加，肋效率虽然在逐渐降低，但是都保持了很高的数值，在99%以上。由文献[10]肋效率曲线可知，肋效率η与mH成反比，且mH=0.174时，η=99%。本研究中翅片高度在20 mm以内，经计算mH均小于0.174，因此其肋效率均大于99%。由此可见，在实际应用中，适当增加翅高不会显著降低其肋效率，是一种可行的增强散热能力的措施。

3.4 翅片厚度对热性能的影响

保持其他结构参数和功率不变，翅片温度及翅片肋效率随翅片厚度的关系如图13所示。

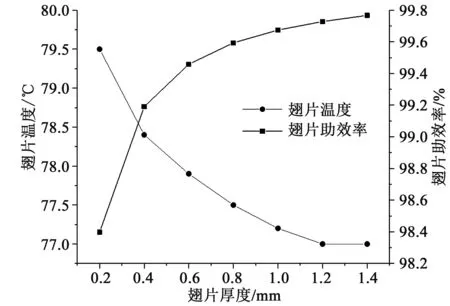
图13 翅片温度及翅片肋效率与翅片厚度的关系Fig.13 Varieties of fin temperature and fin efficiency with fin thickness

由图13可知，随着翅片厚度的增加，翅片温度逐渐降低，但降低趋势逐渐减缓，在厚度增加到1.2 mm后，翅片温度不再随着厚度增加而变化。翅片厚度对翅片温度的影响不大，在翅片厚度由0.2 mm增加到1.4 mm的过程中，翅片温度只降低了2.5 ℃。随着翅片厚度的增加，肋效率也在逐渐增加，在达到1.2 mm以后，肋效率已经接近100%，因此再增加翅片厚度翅片温度不再变化。在翅片厚度为0.2 mm时，肋效率为98.4%，肋效率依然很高，在实际应用中，在满足机械加工能力和翅片强度的前提下，翅片厚度可以尽可能减小，以降低散热器重量。

4 结论

(1)传热系数随着翅片数量、散热器长度及翅片高度增加而逐渐降低；

(2)翅片高度增加会降低翅片的肋效率，在翅片高度20 mm以内，肋效率均在99%以上，翅片肋效率的降低不显著；翅片厚度增大会提高翅片肋效率，翅片厚度达到1.2 mm以后，肋效率已经接近100%；

(3)通过实验对数值模拟进行了验证，模拟与实验差距在3.5%以内，模拟所选用的模型和方法合理，模拟结果可靠。

参考文献：

[1]周建辉,杨春信.太阳花散热器优化设计[J].电子学报,2009,37(2):387-392.

[2]周建辉,杨春信.CPU散热器结构设计与热分析[J].电子机械工程,2006,22(6):16-18．

[3]李艳红,刘吉普.CPU热柱散热器实验研究与温度场数值模拟[J].现代电子技术,2010,33(6):178-180.

[4]张远波.风冷式CPU散热器的热分析及其优化设计[D].武汉：华中科技大学,2006.

[5]李灏,钱新明,陈威.LED太阳花散热器正交试验模拟优化设计[J].照明工程学报,2016,27(1):119-123.

[6]褚旭昭,丁同言,杨洁翔,等.LED散热器散热性能优化分析[J].照明工程学报,2012,23(1):62-65.

[7]向建化,张春良,陈胜, 等.大功率LED太阳花相变散热器数值优化研究[J].广州大学学报(自然科学版),2015,14(2):61-65.

[8]李中,李勇,汤应戈, 等.大功率LED太阳花散热器的结构优化[J].激光与光电子学进展,2012,49:102-201.

[9]陶文铨. 数值传热学[M].2版.西安:西安交通大学出版社,2001.

[10]杨世铭，陶文铨.传热学[M]. 4版.北京:高等教育出版社,2006.