地形突变条件下异重流运动失稳规律
宋以兴李 嘉安瑞冬严忠銮徐亚亚
(1.四川大学水力学与山区河流开发保护国家重点实验室,四川成都 610065;2.中国长江三峡集团,北京 100038)
水库异重流是挟沙浑水进入水库与清水发生相对运动的流动。异重流失稳是指因异重流交界面泥沙垂向扩散加剧或群体性沉降,异重流前锋不再向前运动或运动速度迅速减缓,异重流停止或消失在水库当中。作为泥沙运动力学研究领域的重要课题,异重流的研究对于延长水库寿命、优化水库调度等具有重要的工程意义与学术价值。
在对水库异重流的观测中,严忠銮等[1鄄2]对水库异重流的清浑水交界面和潜入条件进行了研究,并提出新的识别方法和判别式,在紫坪铺水库和小浪底水库中得到良好应用;高亚军等[3]通过观测数据研究了小浪底库区地形与异重流排沙的相互影响。在模型试验方面,李永等[4鄄5]研究了异重流的潜入、前锋形态和推进速度等运动规律;曾曾等[6鄄9]研究了水温分层条件下异重流的运动规律;朱超等[10]利用水沙分离鳃研究了异重流泥沙的垂向沉降速度;Maxworthy等[7鄄12]研究了坡度对异重流运动的影响;Oehy等[13]研究了障碍物对异重流运动的影响;范家骅[14]研究了异重流通过槽宽突扩、突缩段的运动规律。在数值模拟方面,王增辉等[15]建立了基于库区不规则断面的一维非恒定异重流数学模型;Guo等[16鄄21]采用不同的数学模型进行水库异重流模拟研究;Nasr鄄Azadani等[22]开发出一种基于侵入式边界、N鄄S方程的模型,模拟了异重流在复杂地形条件下的传播;胡念三[23]基于FLOW鄄3D建立了三维温差异重流数值模型,并对三峡水库典型支流香溪河河口的异重流运动规律进行了研究;Guo等[16,18鄄29]还研究了坡度对异重流运动规律的影响。
总体来说,上述研究现状反映了目前针对异重流失稳的研究尚相对匮乏。对水库异重流的原型观测多侧重于异重流潜入方面,而对异重流受地形影响的运动规律和失稳情形关注较少;大多数模型试验均以地形均一及环境密度不分层的条件为前提,这与实际情况不相符,且试验研究多侧重于异重流运动速度、前锋形态,并未对异重流失稳成因及条件进行研究;数值模拟方面采用二维各向同性紊流模型,其各向同性的特性有悖于异重流三维特性,而且对于地形突变条件下异重流运动失稳规律的研究较少。本文以紫坪铺水库为例,拟采用三维异重流数学模型,开展地形突变条件下异重流失稳问题的研究。
1 摇异重流计算模型
本文采用Mike3建立三维异重流数学模型,水平方向采用Smagorinsky模型,垂向采用k鄄着模型对N鄄S方程进行封闭和简化。模型包括水动力学模型、紊流模型和泥沙输移扩散方程。
1.1 摇水动力学模型
连续方程:

动量方程:
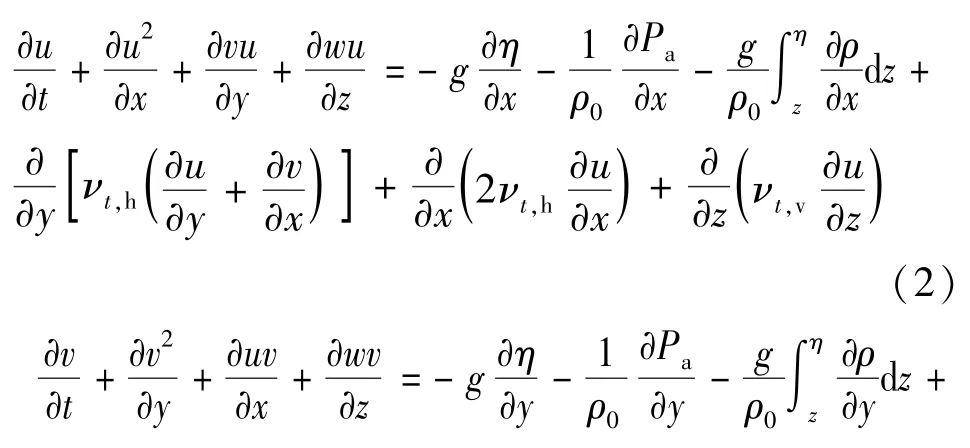

由于水平方向尺度远大于垂向尺度,可以认为水平方向速度远大于垂向速度,故垂向上的加速度非常小,垂向上的动量方程可采用静压假定进行简化,得到下式:

式中:u、v、w分别为x、y、z方向的流速分量,m/s;Pa为当地大气压,Pa;籽0为水体参考密度,kg/m3;籽为水体的混合密度,kg/m3;νt,h与νt,v分别为水平方向和垂向的涡黏系数,m2/s;浊为自由水面高程,m;g为重力加速度,m/s2;t为时间,s。
1.2 摇紊流模型
大量的数值模拟研究表明,小尺度的紊流受网格尺度的限制影响难以得到求解,而且密度分层流动中,不稳定密度分层会加剧动量与标量的紊动输移。因此,紊流模型当中,将涡黏系数νt分为水平向的涡黏系数νt,h与垂向的涡黏系数νt,v进行计算。
a.vt,h采用 Smagorinsky模型计算,其表达式如下:
式中:驻l为特征长度;Cs为Smagorinsky常数,取值在0郾25~1郾0之间;Sxy为主流水平方向的应变率。
b.vt,v由紊动动能k和紊动动能耗散率着求得,k和着采用k鄄着方程进行求解:

式中:c滋、c1着、c2着、c3着、滓k、滓着为经验常数,c滋=0郾09,c1着=1郾44,c2着=1郾92,c3着=0郾3,滓k=1郾0,滓着=1郾3;滓t为普朗特数,取值为 0郾9。
1.3 泥沙输移扩散方程
泥沙输移扩散方程如式(10)所示:


式中:籽s为泥沙密度,石英沙取2650 kg/m3;d为粒径;ν为运动黏度。
1.4 模型求解和参数取值
模型的计算网格在平面上采用非结构化网格,在垂向上采用结构化网格,垂向具体采用了sigma网格以保证地形的连续性。空间离散方面,使用具有二阶精度的线性黎曼数值解来计算水平方向上的对流通量,垂向上界面水流通量采用二阶中心差分格式进行离散,同时水平方向与垂向的扩散通量均采用二阶中心差分格式进行离散;标量方程采用二阶迎风格式。时间离散方面,标量方程水平项与垂向对流项采用二阶隐式Runge鄄Kutta方法,垂向扩散项采用二阶隐式梯形方法。将主库库区划分为7 365伊16(平面伊垂向)个网格,单元网格平面尺寸最小为16 m2,最大为392 m2,垂向网格尺寸为1~6 m。
计算流量采用紫坪铺水库2011年7月21日平均流量,入库流量为 557郾71 m3/s,出库流量为849郾38 m3/s。库区水体的初始泥沙质量浓度取实测值0郾02 kg/m3,入库断面泥沙质量浓度采用原型观测值0郾60 kg/m3,并将入库浑水泥沙质量浓度的10%即0郾06kg/m3作为异重流的最小泥沙质量浓度,泥沙特征粒径取中值粒径11郾94滋m。计算水位为汛期限制水位850m。模型计算采用持续入流工况。
式中:c为水体中悬移质泥沙质量浓度(含沙量),kg/m3;ws为泥沙的沉降速度,m/s。
泥沙的沉降速度通过不考虑泥沙颗粒絮凝作用的静水泥沙颗粒沉速计算公式——斯托克斯沉速公式(Stoke爷s law)计算:
2 试验验证
2.1 异重流试验设计
采用浑水异重流水槽试验(图1),验证计算模型的合理性。该水槽主体为钢架结构,壁面为有机玻璃材质,水槽长为20 m,蓄水深度可达1 m,水槽内宽为0郾4 m。水槽进口处设置4根清、浑进水管道,以保证清水和浑水分开注入。出口处设置溢流堰。试验中根据不同工况,选择不同的浑水泥沙质量浓度及入流流量。试验开始前打开清水管,在水槽中注入一定高度的清水,待液面稳定后打开浑水进口,使浑水流入清水中,观测异重流的产生和运动过程,并在不同断面对异重流不同水层的水体进行采样。采用ZDR温度记录仪对试验水槽内清水的温度以及入流浑水的温度进行测量和记录。采用间接测量法测量泥沙质量浓度,采用紫外分光光度仪测量含沙水样吸光度,并建立水样吸光度与泥沙质量浓度的相关关系。

图1 异重流水槽试验
2.2 工况设定
为保证试验的合理性,选取不同流量和泥沙质量浓度的浑水,由于紫坪铺库区1955—1990年的多年平均泥沙质量浓度为0.572 kg/m3,为低含沙河流,因此试验设计工况下的入流泥沙质量浓度较低,异重流水槽试验工况如表1所示。

表1 异重流水槽试验工况
2.3 模型计算结果的验证
异重流水槽试验中对4个断面进行了采样,如图2所示。断面1所处的区域,由于受到进水管入流的作用,清、浑水剧烈掺混,直到2郾6~3 m时,含沙浑水在横断面处基本能形成横向界面相对平整的浑水下潜,因此断面1处的运动过程不用来表征异重流的运动特征。
图3给出了异重流沿程泥沙质量浓度垂向分布的数值结果与实测结果对比。从各工况的对比情况来看,尽管在个别点处模拟值与实测值存在一定的偏离,但整体上看吻合度良好。

图2 测量断面设置
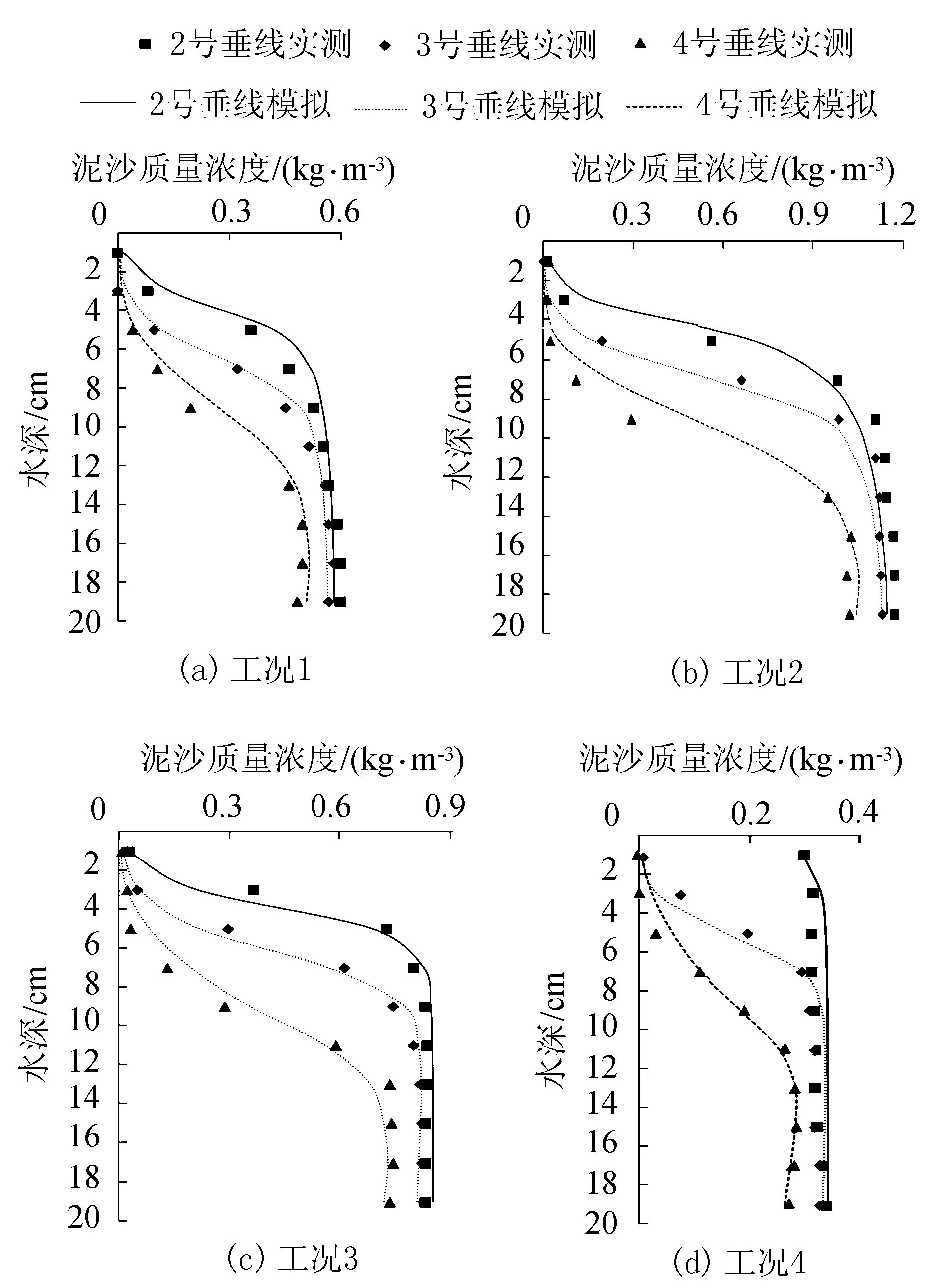
图3 异重流泥沙质量浓度分布实测与模拟对比
为了进一步说明模拟值与实测值的吻合关系,将试验实测数据与模拟数据分别绘制在图4中,可以看出数据都比较均匀地分布在45毅直线的两侧,其中绝对平均误差为0郾31 kg/m3,标准误差为0郾056 kg/m3。说明本文建立的三维异重流计算模型用来研究异重流运动是可行的,其模拟结果较为理想。

图4 异重流中泥沙质量浓度分布实测值与模拟值对比
3 数值模拟结果
3.1 地形变化
紫坪铺水库位于西南山区,是典型的山区河流水库,地形复杂多变,而汶川地震造成的山体滑坡和泥石流等次生灾害使得大量石块、泥沙淤积在水库内,其方量约为530万m3,导致库区地形发生较大变化。根据在2011年3月采用多波束测深技术得到的紫坪铺水库大断面地形实测资料,分析地形沿程变化的情况。库区深泓线在距坝7郾66~6郾21 km范围河段内产生了突变,库底急剧抬升和降低,库底高程由距坝7郾66km处的795m抬升到距坝6郾95km处的809 m,又降低到距坝6郾21 km处的778 m,落差分别达到14 m和31 m,产生了较陡的负坡和顺坡,相当于底部障碍物,如图5(a)所示。在距坝6郾21~5郾65km范围河段内,库区断面产生突扩,断面面积和水面宽度都急剧增大,分别由距坝6郾21 km处的16 897郾1 m2和 323 m 增大为距坝 5郾65 km 处的45153郾8m2和883m,突扩比例分别为 2郾67 和 2郾73,如图5(b)所示。

图5 库区地形沿程变化
为了研究异重流在地形突变条件下的运动失稳规律,在紫坪铺库区中选择典型的地形突变河段,即距坝7郾66~5郾65 km范围内河段,此河段中包括了底部障碍物和断面突扩两种地形突变情况。在此河段内沿着水流前进方向设置8个等间距的观测断面,其中断面A1~A6对应距坝7郾66~6郾21km范围河段,为底部障碍物所在的地形突变区,断面A6~A8对应距坝6郾21~5郾65 km范围河段,为地形突扩所在的地形突变区。在对紫坪铺水库的异重流数值模拟结果进行分析时,将不同断面的异重流前锋前进速度和厚度以及垂向泥沙质量浓度等数据进行统计处理,研究异重流在地形突变条件下的运动规律,探讨地形突变条件下的异重流失稳机制及判别条件。
3.2 地形突变对异重流运动的影响
3.2.1 地形突变对前锋的影响
水库底部异重流前锋的运动规律是判断异重流是否失稳的重要标志,研究河段内异重流前锋的运动速度和厚度沿程变化情况如表2所示。

表2 异重流前锋运动速度和厚度
异重流前锋遇到底部障碍物后,受到阻力作用,前锋运动速度明显减缓,由A1断面的0郾09 m/s减小为A3断面的0郾07 m/s,减小了22郾22%;因为异重流的惯性力远大于其重力,使得它可以翻越障碍物继续流动,在越过障碍物顶部后,异重流沿陡坡流动,缓流变急流,前锋运动速度增大,由A3断面的0郾07 m/s 增大为 A5 断面的 0郾12 m/s,增大了71郾43%;断面面积和水面宽度的增大使得异重流在横向上发生扩散,损失纵向前进的能量,并且急流变缓流,流速明显减小,由A5断面的0郾12 m/s减小为A8断面的0郾08 m/s,减小了33郾33%。
异重流前锋遇到底部障碍物后,在障碍物上游形成壅水,流速减缓,泥沙沉降淤积,前锋厚度减小,由A1断面的11郾07 m减小为A4断面的7郾31 m,减小了33郾97%;越过障碍物顶部后,陡坡上的急流冲刷河床泥沙,前锋厚度快速增加,由A4断面的7郾31 m增加为A6断面的13郾00 m,增加了77郾84%;由于陡坡变缓坡,产生水跃,前锋厚度仍在增加,但断面面积和水面宽度的增大使得异重流在横向上发生扩散,泥沙沉降淤积,前锋厚度的增加趋缓,由A6断面的13郾00 m增加为 A8断面的15郾00 m,增加了15郾38%。
3.2.2 地形突变对泥沙质量浓度的影响
不同断面的泥沙质量浓度垂向分布反映了异重流泥沙的淤积状况,图6显示了31 h时不同断面的异重流泥沙质量浓度在垂向上的分布。由图6可以看出,异重流受到底部障碍物、断面面积和水面宽度增加的影响,底部异重流泥沙质量浓度的垂向分布由类似抛物线分布变为类似对数分布,这说明泥沙发生沉降淤积,使得水库底部泥沙质量浓度增加。

图6 泥沙质量浓度在垂向上的分布
模型中含沙浑水持续入流,不同断面的泥沙质量浓度随时间持续增加,而下游断面的泥沙质量浓度总是小于上游断面,但受地形突变的影响,不同断面的变化情况不同。计算了不同断面的平均泥沙质量浓度以及相比上游断面泥沙质量浓度的变化量和变化率,结果表明,断面A5、A6和A8的泥沙质量浓度变化率的绝对值明显大于其他断面。断面A5和A6是翻越障碍物后的断面,断面A8是断面突扩后的断面,这说明异重流在经过地形突变后,泥沙发生淤积,运动到下游的泥沙减少,因此这些断面的泥沙质量浓度减小得更多。
3.2.3 地形突变对异重流厚度的影响
表3显示了不同断面异重流厚度随时间的变化,可以看出35 h之后异重流厚度基本稳定,反映了异重流经过突变地形一段时间后已经趋于平衡,其规律与异重流前锋有所不同。以37 h为例,在断面A1~A4之间,异重流受到底部障碍物的影响流速减缓,形成壅水,泥沙沉降淤积,异重流厚度减小,由40郾1m 减小为 23郾6 m,减小了 41郾15%;在断面 A4~A7之间,异重流越过障碍物顶部后,急流冲刷使得异重流厚度有所增加,由23郾6 m增大为35郾4 m,增大了50郾00%;在断面A7~A8之间,异重流主要受库区断面突扩的影响,陡坡变缓坡的影响减小,断面面积和水面宽度的增大使得异重流在横向上发生扩散,泥沙沉降淤积,厚度由35郾4 m减小为33郾0 m,减小了 6郾78%。

表3 不同时间对应的异重流厚度___________
3.3 失稳机制及判别条件
3.3.1 异重流持续运动条件及失稳情形
根据异重流的观测资料来看,并不是所有的异重流形成后都能顺利地传播至坝前并排出水库,异重流形成至运动到坝前所满足的输沙特性及所受阻力特性条件,即异重流的持续运动条件主要包括以下几个因素:淤有一定的洪峰流量持续时间及入库流量;于有一定的泥沙质量浓度及细沙比例;盂库区地形变化不大;榆适宜的排沙时机。
从试验研究及原型观测结果来看,异重流失稳表现为异重流交界面的群沙性沉降,异重流不再向前运动或运动趋势减弱,或者因泥沙垂向输移扩散使得异重流厚度不断增加等现象,而会造成异重流失稳的原因包含以下几种:淤失去后续浑水补充;于密度分层;盂地形变化。本文主要研究了地形变化即底部障碍物和断面突扩导致的异重流失稳情形。
3.3.2 底部障碍物条件下失稳机制
持续的入流条件可以给异重流提供能量补充,但地形突变仍会导致其失稳。底部障碍物首先会对异重流产生阻碍作用,使得异重流运动速度减缓,一部分泥沙停止运动并沉降淤积;在障碍物上游会形成壅水,并产生向上游移动的水跃,带动部分泥沙向上游运动。因此异重流泥沙质量浓度降低,前锋及异重流厚度减小。
3.3.3 断面突扩条件下失稳机制
断面突扩即库区断面面积和水面宽度增加,首先增大了可淤面积,清浑水层之间产生掺混,上层部分清水越过交界面进入浑水层中,加大了异重流流量,降低了泥沙质量浓度;清浑水层之间的掺混和突扩段的水跃,使得能量产生损失,导致流速明显降低,泥沙沉降淤积,异重流底部泥沙质量浓度变大,异重流交界面降低,即异重流厚度减小。
4 结 论
a.本文建立的三维异重流计算模型,考虑了异重流在水平方向与垂向的紊动特性差异,以及河床淤积等因素对泥沙传输的影响。水槽试验表明该模型能够模拟出自然环境下异重流在库区的运动过程。
b.根据计算结果,分析了水库底部障碍物对异重流前锋、泥沙质量浓度和厚度等的影响,研究了库底障碍物条件下异重流运动失稳规律,并得到此种情形下异重流失稳的判别条件为:淤异重流运动速度减缓;于异重流泥沙质量浓度降低;盂前锋及异重流厚度减小。
c.根据计算结果,分析了断面突扩对异重流前锋、泥沙质量浓度和厚度等的影响,研究了断面突扩条件下异重流运动失稳规律,并得到此种情形下异重流失稳的判别条件为:淤异重流运动速度减缓;于异重流泥沙质量浓度的垂向分布由类似抛物线分布变为类似对数分布;盂异重流厚度减小。
[1]严忠銮,安瑞冬,李嘉,等.浊度型清浑水交界面识别方法及其在水库异重流观测中的应用[J].水利水电科技进 展,2013,33(6):71鄄75.(YAN Zhongluan,AN Ruidong,LI Jia,et al.Turbid interface identification method of turbidity currents and its application in field observation atZipingpu Reservoir[J].Advancesin Science and Technology of Water Resources,2013,33(6):71鄄75.(in Chinese))
[2]李书霞,夏军强,张俊华,等.水库浑水异重流潜入点判别条件[J].水科学进展,2012,23(3):363鄄368.(LI Shuxia,XIA Junqiang,ZHENG Junhua,et al.Prediction criterion of turbidity current formation in reservoir[J].Advances in Water Science,2012,23(3):363鄄368.(in Chinese))
[3]高亚军,陆永军,许慧.小浪底水库异重流对库区河床冲淤的影响[J].河海大学学报(自然科学版),2009,37(2):240鄄244.(GAO Yajun,LU Yongjun,XU Hui.Effect of density currents in Xiaolangdi Reservoir on riverbed erosion and deposition[J].Journal of Hohai University(Natural Sciences),2009,37(2):240鄄244.(in Chinese))
[4]李永,李嘉,安瑞冬.水沙两相流ASM模型在浑水异重流计算中的应用及模型试验研究[J].四川大学学报(工程科学版),2009,41(4):102鄄108.(LI Yong,LI Jia,AN Ruidong.The application of water鄄sediment two phase flow ASM model in the density current of turbid water and related model test study[J].Journal of Sichuan University(Engineering Science Edition),2009,41(4):102鄄108.(in Chinese))
[5]RUI DONG A N,JIA L I.Characteristic analysis of the plunging of turbidity currents [J]. Jounal of Hydrodynamics:Series B,2010,22(2):274鄄282.
[6]曾曾,李嘉,安瑞冬,等.低含沙量异重流运动规律及其对水温分布的影响[J].水动力学研究与进展:A辑,2016,31(3):346鄄354.(ZENG Ceng,LI Jia,AN Ruidong,et al.The motion law of the density current with low sediment content and influence on water temperature distribution[J].Chinese Journal of Hydrodynamics,2016,31(3):346鄄354.(in Chinese))
[7]MAXWORTHY T.Experimentson gravity currents propagating downslopes:part 2 the evolution of a fixed volume of fluid released fromclosed locks into a long,open channel[J].Journal of Fluid Mechanics,2010,647:27鄄46.
[8]林挺.层结水体中异重流沿坡运动的试验研究[D].杭州:浙江大学,2016.
[9]解岳,李璇,孙昕.出水口位置对异重流运动及泥沙分布的影响[J].水资源保护,2017,33(6):114鄄120.(XIE Yue,LI Xuan,SUN Xin.Influence of different outlet positions on density currents movements and sediment distributions[J].Water Resources Protection,2017,33(6):114鄄120.(in Chinese))
[10]朱超,邱秀云,严跃成.垂向异重流式水沙分离鳃水沙分离机理浅析[J].水利水电科技进展,2009,29(5):20鄄23.(ZHU Chao,QIU Xiuyun,YAN Yaocheng.Analysis of mechanism of vertical鄄component density flow water鄄sediment separation device[J].Advances in Science and Technology of Water Resources,2009,29(5):20鄄23.(in Chinese))
[11]周磊,安瑞冬,谭升魁,等.水库异重流淤积成因分析及前锋运动规律[J].水利水电科技进展,2012,32(2):6鄄10.(ZHOU Lei,AN Ruidong,TAN Shengkui,et al.Study on reservoir sedimentation caused by turbidity currents and experimental study on front movement[J].Advances in Science and Technology of Water Resources,2012,32(2):6鄄10.(in Chinese))
[12]DAI A.Experiments on gravity currents propagating on different bottom slopes[J].Journal of Fluid Mechanics,2013,731(3):117鄄141.
[13]OEHY C D,SCHLEISS A J.Control of turbidity currents in reservoirs by solid and permeable obstacles[J].Journal of Hydraulic Engineering,2007,133(6):637鄄648.
[14]范家骅.浑水异重流槽宽突变时的局部掺混[J].水利学报,2005,36(1):1鄄8.(FAN Jiahua.Local entrainment of turbid density current in width abrupt changed channel[J].Journal of Hydraulic Engineering,2005,36(1):1鄄8.(in Chinese))
[15]王增辉,夏军强,李涛,等.水库异重流一维水沙耦合模型[J].水科学进展,2015,26(1):74鄄82.(WANG Zenghui,XIA Junqiang,LI Tao,et al.One鄄dimensional coupled model for predicting turbidity currents in reservoirs[J].Advances in Water Science,2015,26(1):74鄄82.(in Chinese))
[16]GUO Y,ZHANG Z,SHI B.Numerical simulation of gravity current descending a slope into a linearly stratified environment[J].Journal of Hydraulic Engineering,2014,140(12).DOJ:04014061.
[17]谭升魁,王锐,安瑞冬,等.基于组分输运模型和RNGk鄄着模型的浑水异重流数学模型研究及其应用[J].四川大学学报(工程科学版),2011,43(增刊1):48鄄53.(TAN Shengkui,WANG Rui,AN Ruidong,et al.Research and application of numerical model of turbidity currents based on species transport model and RNGk鄄着model[J].JournalofSichuan University(Engineering Science Edition),2011,43(Sup1):48鄄53.(in Chinese))
[18]BIRMAN V K,BATTANDIER B A,MEIBURG E,et al.Lock exchange flows in sloping channels[J].Journal of Fluid Mechanics,2007,577:53鄄77.
[19]BIRMAN V K,MEIBURG E,UNGARISH M.On gravity currents in stratified ambient[J].Physics of Fluids,2007,19(8):425鄄441.
[20]DAI A,OZDEMIR C E,CANTERO M I,et al.Gravity currents from instantaneous sources down a slope[J].Journal of Hydraulic Engineering,2012,138(3):237鄄246.
[21]DAI A.Gravity currents propagating on sloping boundaries[J].Journal of Hydraulic Engineering,2013,139(6):593鄄601.
[22]NASR鄄AZADANIM M,MEIBURG E.Turbins:an immersed boundary,Navier鄄Stokes code for the simulation of gravity and turbidity currents interacting with complex topographies[J].Computers&Fluids,2011,45(1):14鄄28.
[23]胡念三.香溪河河口温差异重流三维数值模拟研究[D].宜昌:三峡大学,2013.

