基于F-DPM的行人实时检测

戴植毅，黄妙华

(1.武汉理工大学 汽车工程学院，湖北 武汉 430070；2.武汉理工大学 现代汽车零部件技术湖北省重点实验室，湖北 武汉 430070)

目标检测是计算机视觉中一个重要的课题。行人检测作为其中的子问题，其在智能监控、辅助驾驶系统和机器人视觉等领域有着广阔的应用前景和市场价值。而行人检测易受人体姿态、复杂环境以及存在遮蔽问题的影响，因此如何高效的进行检测一直是研究热点。

目前，基于视觉的行人检测方法主要分为机器学习和深度学习两大类。机器学习的主要流程分为3步：①待检图像候选区域生成；②提取候选区域图像特征；③使用分类器对所提取的特征进行候选验证。例如在文献[1]中，Cheng等使用滑动窗口[2]产生候选区域，候选区域特征选用的是Haar特征[3]，采用Ada Boost级联SVM(support vector machine)的方式以加快运算速度[4]。文献[5]中，Wu等采用经典的DPM(deformable parts model)[6]模型，通过使用BING(binarized normed gradients)[7]和EdgBoxes[8]取代滑动窗口加速候选区域生成，在此基础上形成图像金字塔，最后由DPM模型对候选区域完成验证。2014年，Dollar等提出了ACF(aggregated channel features)特征[9]，将HOG(histogram of oriented gradient)特征改进后与LUV颜色特征相结合，而后用Real Ada Boost分类器进行检测，检测的速度为140 ms，相比以往的非GPU(graphic processing unit)的机器学习算法有了很大的提升。

在深度学习中，检测对象特征的概念被模糊化，转而由神经网络通过大量样本自行学习获得。越来越多的学者将研究重点转向感兴趣区域提取(region of interesting, ROI)和深度学习(deep learning, DL)。其中ROI大大减少了候选区域的数量从而提升了候选区域生成速度；卷积神经网络(convolutional neural network, CNN)整合了特征提取和验证两个过程，同时对目标的识别效果显著[10]，故在目标检测问题上CNN得到了广泛应用。例如前沿的R-CNN[11]、SPP-Net[12]、Fast R-CNN[13]、Faster R-CNN[14]、YOLO(you only look once)[15-16]等算法均是通过构建CNN网络来实现目标物的检测。文献[15]中对YOLO算法进行了试验，简单网络下VOC 2007数据集的检测速度为13 ms，平均准确率为76.8%；复杂网络下的检测速度为25 ms，平均准确率为78.6%。

这两类方法都有各自的优缺点，机器学习的检测实时性不好，但是对硬件的要求低，针对具体实际问题的应用性更强；深度学习需要使用GPU进行加速，硬件要求制约了其实际应用。针对上述问题，文献[17]提出通过傅里叶变换能够对模板与特征的卷积运算进行加速，其检测速度可以达到60 ms。由此笔者寻求了一折中的算法F-DPM，通过快速傅氏变换(fast fourier transformation，FFT)将检测效果优异的DPM算法进行了加速优化，并且对特征金字塔的搭建进行了改进，使其在CPU下能满足实时性要求。

1 DPM算法相关理论

DPM本质上是HOG特征的扩展，大体思路与HOG一致。通过计算梯度方向直方图，然后用SVM训练得到待检测物体的梯度模型模板，将模型模板和目标进行匹配。DPM只是在模型上做了很多细致的改进。DPM特征除利用梯度算子计算样本的梯度特征外，还引入了弹簧变形模型[18]，提出了分离检测目标对象的组件和部件的方法。每个DPM模型都包含一个根滤波器和i个可变部件滤波器，其中单个可变部件滤波器的分辨率是根滤波器的两倍，如图1所示。由于根滤波器和部件滤波器的分辨率不同，因此对于待测样本采集DPM特征，也可看作是对图片在两种不同分辨率下采集HOG特征。检测算子进行目标匹配计算得分时，使用滑动窗口扫描法，检测窗口的得分等于根滤波器与部件滤波器的得分之和，其可视化后如图1(c)所示。由于DPM采用的是多尺度的检测方式，每个部件的得分是此部件的各个空间尺度位置得分的最大值，而每个部件的空间位置得分是部件在该子窗口上滤波器的得分减去变形花费。

DPM特征也需进行HOG特征的提取，根滤波器只使用了8×8的Cell，并将该细胞单元与其对角线临域的4个细胞单元做归一化操作，如图2所示。之后提取有符号的HOG梯度，将0～360°度分成18个梯度向量，构成特征的前18维；再提取无符号的HOG梯度，将0～360°度分成9个梯度向量，构成特征的中间9维；将无符号的HOG梯度按细胞单元累加，得到最后4维，最终得到一个18+9+4=31维的特征。检测窗口的大小选取120×40，故根滤波器的特征为31×15×5=2 325维。同理，部件滤波器的Cell为4×4，只将0～360°度分成9个梯度向量，窗口大小为24×24，故其特征为4×9×6×6=1 296维。之后运用图像样本训练Latent SVM分类器得到根滤波器模板和部件滤波器模板。算法的检测流程如图3所示，最后根据模板与窗口进行匹配打分，选择最高分值的窗口作为检测结果。

图1 根模型、部件模型和窗口得分

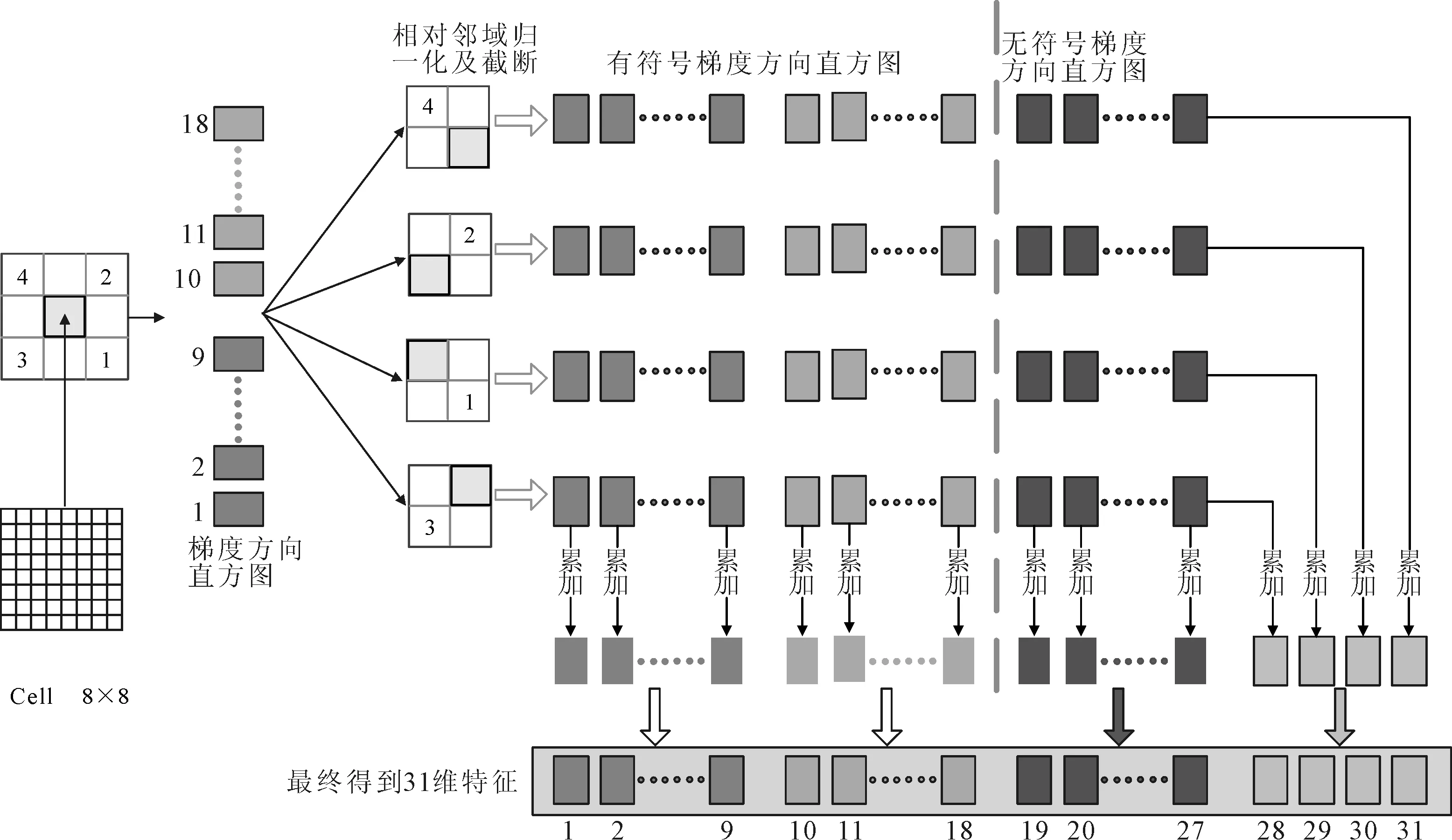
图2 DPM改进HOG特征原理

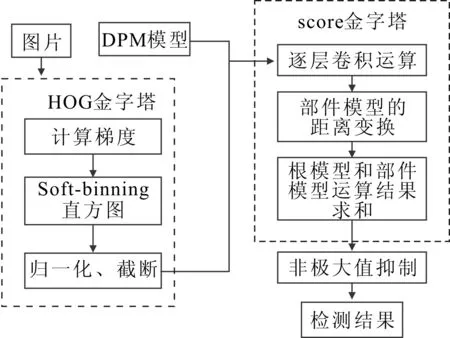
图3 DPM检测流程

对于单个部件模型的详细响应得分按式(1)计算。

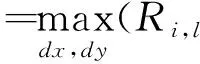
di·φd(dx,dy))

(1)

式中：l为图像金字塔的第l层；点(x,y)为训练的理想模型的位置；Di,l(x,y)为第i个部件在第l层图像金字塔的(x,y)点的最大得分；Ri,l(x+dx,y+dy)为该部件分类器与对应特征向量卷积后得到的响应得分；di·φd(dx,dy)为该部件相对理想位置的偏移损失得分；di为偏移损失系数；φd(dx,dy)为部件模型的理想位置与组件模型的检测点间的距离。

整个检测窗口的得分按式(2)计算。

score(x0,y0,l0)=R0,l0(x0,y0)+

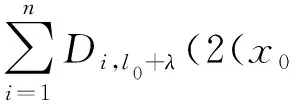
(2)

式中：score(x0,y0,l0)为在l0层特征金字塔中以(x0,y0)为锚点的窗口分数值；R0,l0(x0,y0)为l0处的根模型的响应分数；υi为部件模型锚点和理想检测点之间的坐标偏差；b为不同模型组件之间的偏移系数，用以将窗口与模型模板对齐。

2 DPM加速改进

运用图3的检测流程进行行人检测其检测效果能够达到要求，但是检测速度未能达到实时性的要求，因此需对其进行加速优化。其中，生成HOG金字塔过程和模型模板与每一层HOG金字塔卷积的过程耗费的时间比例最大，笔者对其分别进行了加速优化。

2.1 FFT卷积运算加速

模板与新窗口的卷积过程本质上相当于两个等维向量的点积，在时域下两个n维相向卷积，其计算的复杂度为Ο(n×n)。而将向量从时域空间转到频域空间，在频域中对两向量进行卷积，其卷积运算的复杂度为Ο(nlgn)。由此可见随着维度n的增长，频域的卷积运算的复杂度相对时域的复杂度会大大降低，而DPM特征为2 325维和1 296维的向量，对其进行时频的转换，从理论上是可以达到节省运算时间的效果。

针对图像特征为离散的序列，快速傅里叶变换[19]FFT能够很好地完成时频域的转换。但是由于HOG特征金字塔隔层的图像大小不同，转换到时域后不能直接与模板相乘，因此HOG特征金字塔和模板需填充至同等大小，再转到频域卷积。由FFT转到频域的模板可以事先存到频域模板库中，这样在实时检测时就可以省去模板转化的时间，相应检测流程如图4所示。

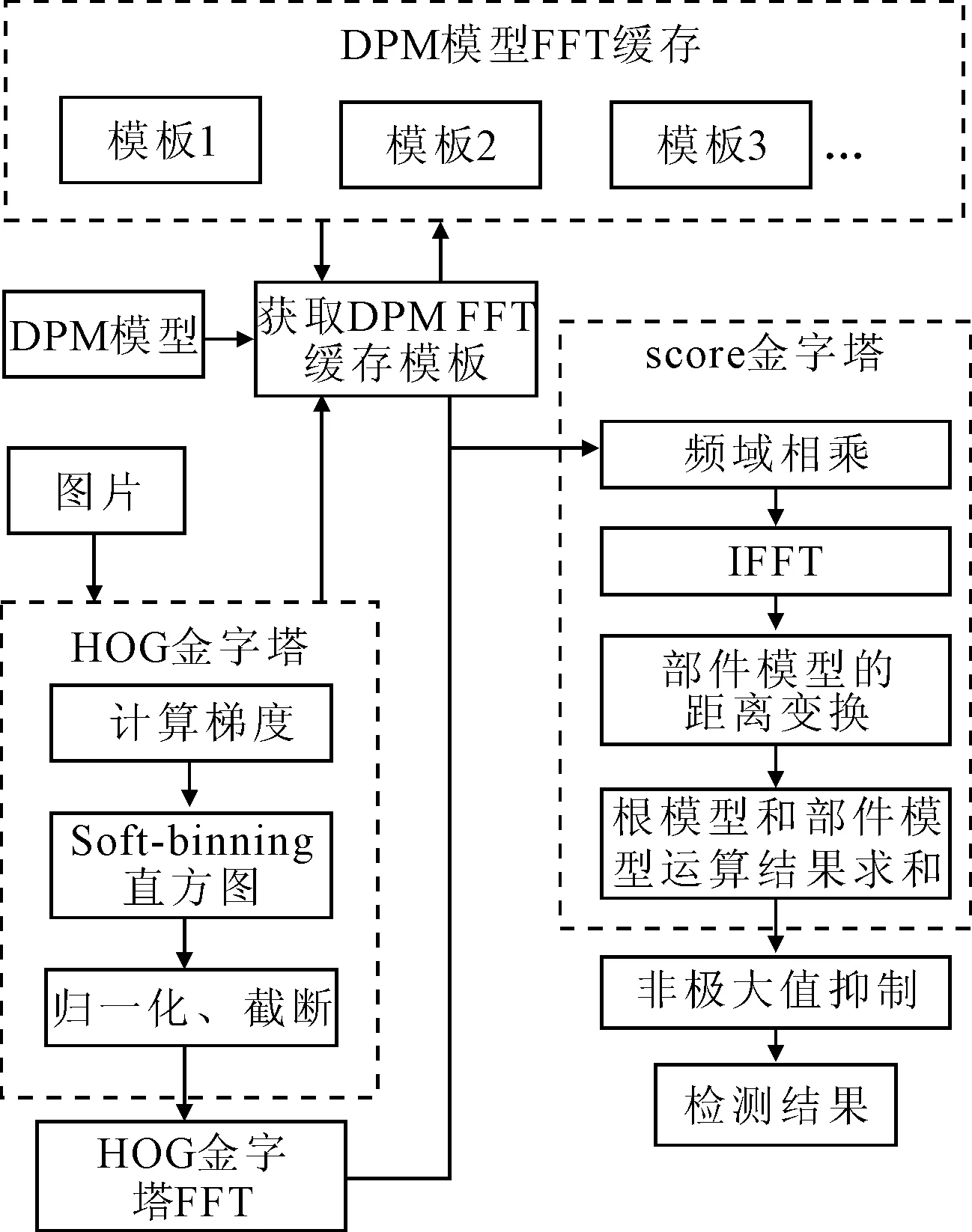
图4 F-DPM检测流程

2.2 HOG金字塔快速搭建与分层检测

根据式(2)计算每一层HOG金字塔中窗口分数，本质就是用训练好的模型模板与HOG金字塔的每一层进行滑动卷积，式(2)中可知l层与l+λ层的图像分辨率为两倍关系，而进行卷积的模型模板是固定的，因此只需计算l层的HOG特征即可，相应的l+λ、l+2λ层等均可通过对l层降维得到。在降维过程中，可先计算第l层的soft binning直方图，其中l大于等于1并且小于λ，然后采用高分辨率下4个值拟合低分辨率下一个值，不断计算出第l+λ层soft binning直方图，l+2λ层soft binning直方图，以此类推。再根据soft binning直方图通过归一化和截断获得各层的HOG特征。因此对于整个HOG特征金字塔，只需计算1～λ层的HOG特征即可，其余的各层均可通过降维得到，从而提升了运算效率。相应的HOG特征金字塔构建过程如图5所示。

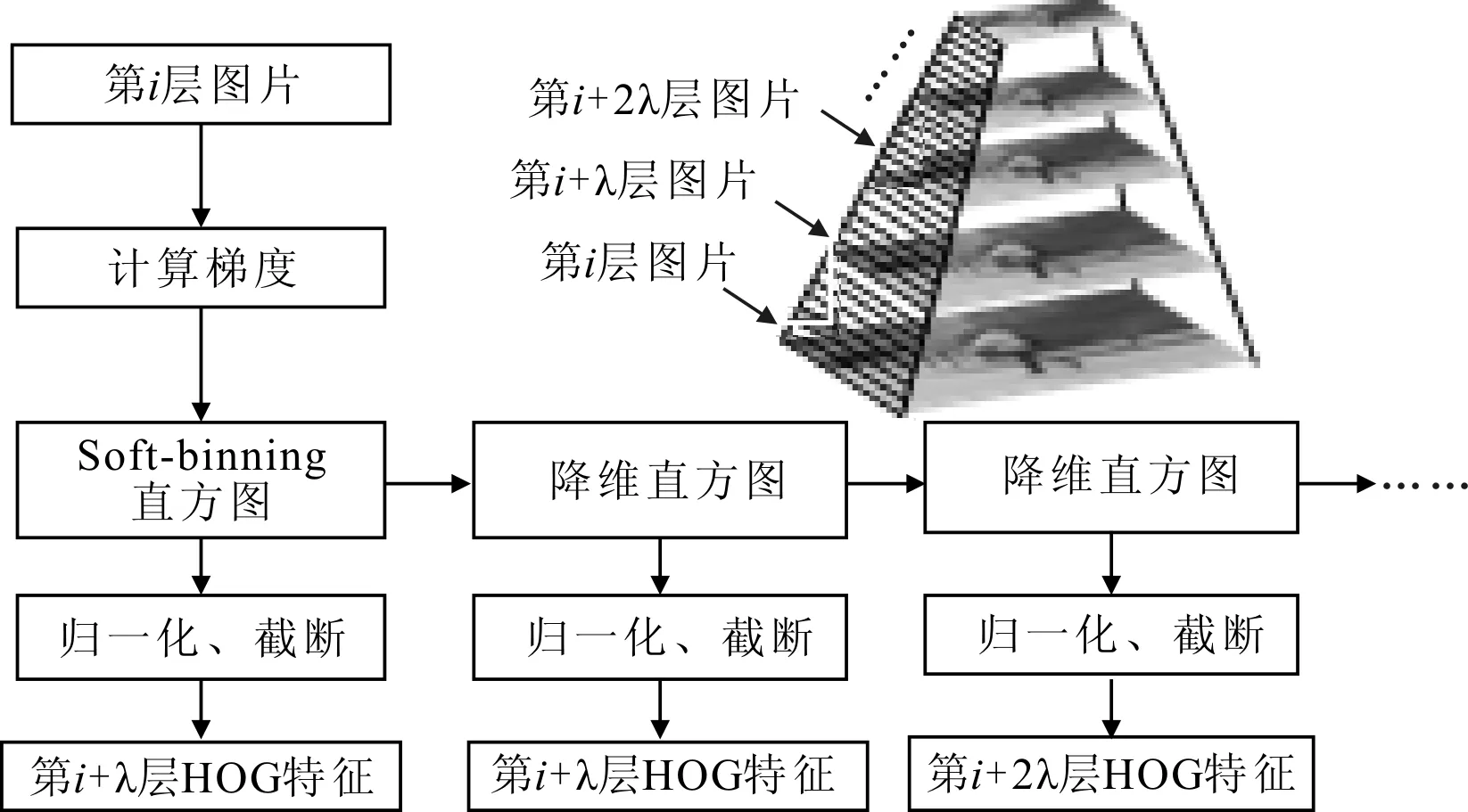
图5 特征金字塔降维构建原理

在DPM算法中，训练得到的模型模板有根滤波器F0和可变部件滤波器Fn两类，如图6所示。根模型主要是对物体潜在区域进行定位，获取可能存在物体的位置，但是否真的存在所期望的物体，还需要部件模型进一步确认。因此，笔者先只采用根模型，在根模型的HOG特征的k层上进行卷积运算，得到根模型的计算结果，然后各层计算结果进行非极大值抑制，筛选候选位置。对于每一个候选位置，回到部分模型所在的k+λ层，在各个部分模型期望位置的邻域中，计算部分模型与HOG特征卷积结果减去形变惩罚量的最大值，求得该候选位置的根模型与部分模型的最终得分。如果这个得分大于阈值，则该位置存在待检测的物体。所有计算完成后，删去分值较低并且与分值高的检测结果有很高重合面积的位置，得到最终的检测结果。

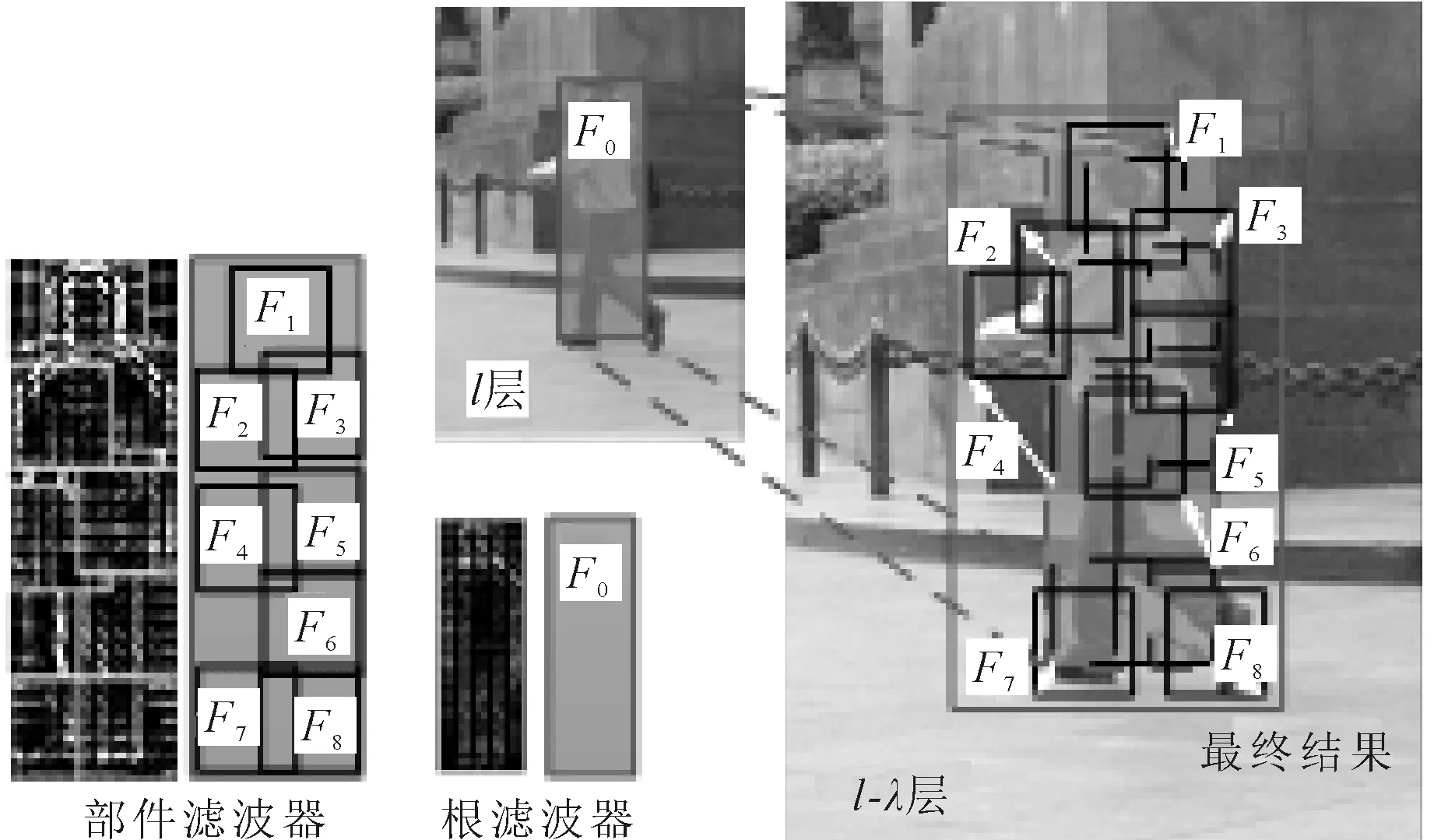
图6 分层检测原理

3 试验仿真与结果分析

完成算法改进之后，对该算法在PC端进行了实验验证。算法的运行环境如下：内存为8 G，CUP为Intel酷睿i7处理器，主频为3.6 GHz。

笔者采用INRIA数据集作为试验的图像数据集，该数据集中人的姿态和光照条件等相对全面，包含了城市、海滩和山等各种场景，较为适合做行人检测。该数据集的训练集具有正样本614张(包含2 416个行人),负样本为1 218张;测试集的正样本为288张(包含行人1 126个),负样本453张。数据集部分图像如图7所示。

图7 部分INRIA训练正样本图

利用其中的训练集来训练分类器，通过测试集来说明分类器检测的可靠性。本文以查准率(precision)和召回率(recall)作为预测结果的评价指标，计算公式如下：

(3)

(4)

式中：TP为测试集的真正例数；FP为假正例数；FN为假反例数。

为验证F-DPM算法的准确性与检测速度，笔者将DPM、ACF和YOLO算法作为对比算法，3种算法的相应检测性能如表1所示。3种算法中YOLO的检测速度和检测准确性都是最高的，而由DPM改进的算法F-DPM其检测速度提升幅度巨大，较ACF算法也快了一倍，并且其检测的准确性较ACF算法表现也更加优异，这在机器学习算法中已属于不错的成绩。

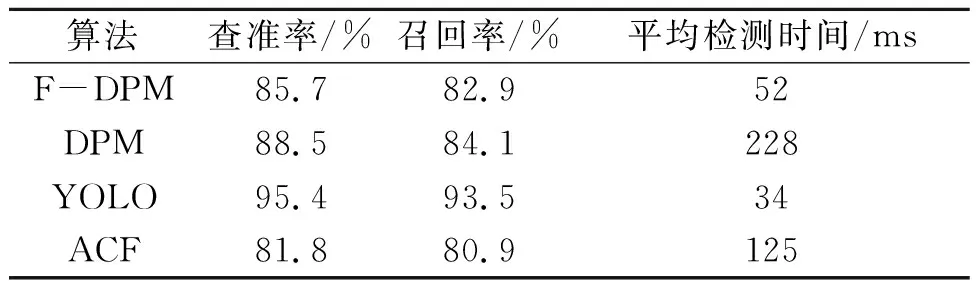
表1 结果参数对比

为检验本算法的检测效果，分别对其检测效果和检测速度进行比较，检测结果对比图如图8所示。对比图8(a)的检测结果，可以看出这3种算法都能够将图片中的行人检测出来，但目标定位的精确度ACF算法相对而言较差。对比图8(b)，F-DPM与YOLO均能准确检测出目标，而ACF存在目标漏检。图8(c)的场景为一个街区，该图中只有F-DPM准确无误的检测出图中的目标；而ACF算法误将橱窗和街边的衣物检测为行人，属于误检现象，并且其中的女性行人检测框，融合筛选效果较差；YOLO算法的检测框效果良好，当时也存在误将衣物识别为行人的误检现象。

图8 检测效果对比

分析3种算法的原理，不难对上述检测的结果做出解释。ACF算法只是简单的将表征梯度信息的HOG特征和表示颜色信息的LUV通道特征进行了结合，形成ACF特征。该算法虽然较以往的CPU机器学习算法其检测速度相对较快，但如遇到背景复杂或者行人着装与背景相似的情形，易出现漏检。同时ACF特征相对DPM特征而言较为粗糙，这就造成误将图8(c)中橱窗和街边衣服识别为行人的误检情形。而DMP算法中有根滤波器和部件滤波器两种模板，根滤波器先快速对图形筛选出潜在的检测目标位置，而后再由部件滤波器对其进行精确判断，先粗筛后精筛，保证了检测的准确性。而YOLO算法其主要优势是用来做多分类问题，对于单类问题的细致检测效果亦没有DPM算法好，因此YOLO算法在总体检测效果良好的情形下，有时会将与人相似的物体误检为行人。

从检测速度、检测准确性以及检测的图像效果的算法对比可见，通过FFT变换将卷积计算由时域转到频域，以及降维后快速得到图像特征金字塔的方法，对检测的速度有了很大的提升。而使用分层卷积的方法，同样对检测过程进行了加速，并且对行人能够更加精确地检测其位置。

4 结论

笔者基于DPM算法提出了一种新的F-DPM算法，该算法通过FFT将特征与模板的卷积运算从时域转到频域，并通过降维的方式拟合构建特征金字塔，这两种改进大大提升了F-DPM的检测速度。以查准率、召回率和平均检测时间对F-DPM的检测准确性和检测速度进行了准确评价。对比ACF、YOLO算法，F-DPM很好地兼顾了检测速度和检测效果，使其能够在CPU下基本满足检测的实时性要求，这对行人检测推向实际应用做出了一定的贡献。

参考文献：

[1] Cheng W C, Jhan D M. A Cascade Classifier Using Adaboost Algorithm and Support Vector Machine for Pedestrian Detection[C]∥ IEEE International Conference on Systems, Man, and Cybernetics. [S.l.]:IEEE, 2011:1430-1435.

[2] Zhu Q, Yeh M C, Cheng K T, et al. Fast Human Detection Using a Cascade of Histograms of Oriented Gradients[C]∥2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. [S.l.]: IEEE, 2006:1491-1498.

[3] Zhao X, Heng C. Context Modeling for Facial Landmark Detection Based on Non-adjacent Rectangle (NAR) Haar-like Feature[J]. Image & Vision Computing, 2012,30(3):136-146.

[4] Schapire R E. The Convergence Rate of AdaBoost[C]∥ 2010 Conference on Learning Theory. Haifa:[s.n.], 2010:308-309.

[5] Wu X, Kim K Y, Wang G, et al. Fast Human Detection Using Deformable Part Model at the Selected Candidate Detection Positions[M]. [S.l.]: Springer International Publishing, 2015.

[6] Felzenszwalb P, Mcallester D, Ramanan D. A Discriminatively Trained, Multiscale, Deformable Part Model[C]∥ IEEE Conference on Computer Vision and Pattern Recognition. [S.l.]:IEEE, 2008:1-8.

[7] Cheng M M, Zhang Z, Lin W Y, et al. BING: Binarized Normed Gradients for Objectness Estimation at 300fps[C]∥ Computer Vision and Pattern Recognition. [S.l.]: IEEE, 2014:3286-3293.

[8] Zitnick C L, Dollár P. Edge Boxes: Locating Object Proposals from Edges[C]∥ European Conference on Computer Vision. [S.l.]:Springer, 2014:391-405.

[9] Dollar P, Appel R, Belongie S, et al. Fast Feature Pyramids for Object Detection.[J].IEEE Transactions on Pattern Analysis & Machine Intelligence, 2014,36(8):1532-1545.

[10] 吴正文.卷积神经网络在图像分类中的应用研究[D].成都：电子科技大学,2015.

[11] Girshick R, Donahue J, Darrell T, et al. Rich Feature Hierarchies for Accurate Object Detection and Semantic Segmentation[C]∥Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. [S.l.]:IEEE, 2014:580-587.

[12] He K, Zhang X, Ren S, et al. Spatial Pyramid Pooling in Deep Convolutional Networks for Visual Recognition[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2015,37(9):1904-16.

[13] Girshick R.Fast R-CNN[C]∥ IEEE International Conference on Computer Vision. [S.l.]:IEEE Computer Society, 2015:1440-1448.

[14] Ren S, He K, Girshick R, et al. Faster R-CNN: Towards Real-time Object Detection with Region Proposal Networks[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2015,39(6):1137-1149.

[15] Redmon J, Divvala S, Girshick R, et al. You Only Look Once: Unified, Real-time Object Detection[C]∥ Computer Vision and Pattern Recognition. [S.l.]:IEEE, 2016:779-788.

[16] 刘建国，罗杰，王帅帅，等.基于YOLOv2的行人检测方法研究[J].数字制造科学，2018，16(1)：50-54.

[17] Dubout C. Exact Acceleration of Linear Object Detectors[C]∥ European Conference on Computer Vision. [S.l.]:Springer-Verlag, 2012:301-311.

[18] Fischler M A, Elschlager R A. The Representation and Matching of Pictorial Structures[J]. IEEE Transactions on Computers, 2006,C-22(1):67-92.

[19] Rao K R, Kim D N, Hwang J J.快速傅里叶变换:算法与应用[M].万帅，杨付正，译.北京：机械工业出版社,2013.