基于改进模糊控制的潜艇运动仿真研究
黄 斌 彭利坤 吕帮俊
(海军工程大学动力工程学院 武汉 430033)
0 引 言
潜艇在水下航行时受到多种因素的影响,需要通过不断的操舵来保持潜艇定深航行.当前,对于船舶自动操舵控制的研究很多,大部分集中在对水面船舶航向的控制,而对于潜艇在垂直面的运动控制方面相对较少.其中PID控制[1-2]、鲁棒控制[3]、自适应神经网络控制[4]、模糊控制等控制方法在潜艇垂直面的运动中取得了较好的效果.
常规PID控制以被控参数误差作为输入,通过对误差信号进行比例、积分和微分的处理后,输出控制量对系统进行控制[5-6].但是由于潜艇本身质量较大,操舵对于潜艇的运动的相应有明显的时间滞后性,因此常规的PID控制方法虽然能达到控制潜艇定深定常运动的效果,但是舵机的动舵幅度与频率较大,容易对舵机造成损耗,因此,本文设计一种模糊控制器来对潜艇的垂直面运动进行控制,通过较平缓的操舵曲线来控制潜艇垂直面定深定常运动,具有更加优越的可操作性.
1 潜艇垂直面运动数学模型
当潜艇在垂直面内作弱机动时,运动参数Δu,w,q,δb,δs为小量时,有
(1)
式中:第一式为水平直线运动方程,为水平直线运动的速度u与水平方向阻力X之间的简单函数关系,潜艇垂直面运动主要考虑式(1)中的二、三式.代入线性水动力式,计及剩余静载P,Mp和扶正力矩Mθθ的垂直面操纵运动线性方程为
Z0+Zδbδb+Zδsδs+P
M0+Mδbδb+Mδsδs+XTzT+MP+Mθθ
(2)
式中:m为潜艇质量;u为潜艇水平方向速度分量;w为潜艇垂直方向速度分量;δb和δs分别为首舵和尾舵舵角;P和MP分别为剩余静载力和力矩,Mθθ为扶正力矩,其余带下标的均为潜艇垂直面运动的水动力系数.采用四阶龙格库塔法对式(2)进行迭代求解,得到潜艇的运动规律.
2 模糊控制器的设计
潜艇垂直面运动主要通过控制首舵和尾舵来保持和改变潜艇的运动状态,因此,模糊控制器的输出量设定为首舵和尾舵的舵角.按照潜艇运动的特点,本文设计两个模糊控制器,一个用深度的误差量作为输入控制首舵,另一个用纵倾的误差量作为输入控制尾舵,两个模糊控制器共同作用控制潜艇的垂直面运动.
2.1 误差及控制量的模糊化
深度模糊控制器的输入为深度偏差E和深度偏差的变化率Ec,为了达到精确控制的效果,将E,Ec以及控制量δb的数值划分为13个模糊集,即:负大(NB)、负大中(NBM)负中(NM)、负中小(NMS),负小(NS)、负小零(NSZ),零(ZE)、正小零(PSZ)、正小(PS)、正中小(PMS)、正中(PM)、正大中(PBM)、正大(PB).深度偏差E的论域设定为{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6},其他变量的设定类似,只是数值不同.经过反复试验,选择标准正态分布作为隶属度函数.即
(3)
式中:μ为E相对于论域值Ek的隶属度.特殊情况,当E>6时,取正大的隶属度为1,当E<-6时,取负大的隶属度为1.
纵倾模糊控制器的设计与深度模糊控制器类似,将纵倾偏差及纵倾偏差变化率和控制量δs划分为13个模糊集,选择标准正态分布作为隶属度函数.
新旧标度震级震级中误差显示,宽频带面波震级MS(BB)相对面波震级 MS、新 ML相对于旧 ML收敛程度都有一定程度的改善。
2.2 模糊控制规则的确定
利用深度和纵倾误差,设计合理的模糊控制规则来确定首舵和尾舵,是决定控制器好坏的重要环节.结合潜艇垂直面运动的操纵规律:首舵δb>0时,首舵作用力和力矩对潜艇产生上浮效果,反之对潜艇产生下潜效果.尾舵δs>0时,尾舵作用力和力矩对潜艇产生首倾效果,反之对潜艇产生尾倾效果.按照上述规律并结合部队实际操舵经验,首舵控制深度的模糊控制规则见表1.
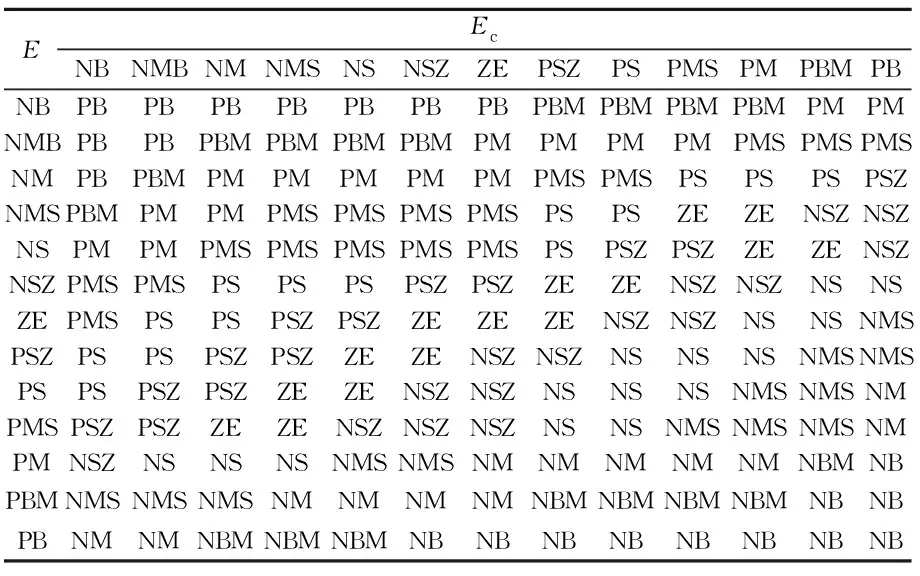
表1 首舵控制深度的模糊控制规则
模糊控制语言可表示为
ifE=EiandEc=Ecj
thenU=Uij
(4)
式中:i=1,2,…,13;j=1,2,…,13.表1结合首舵角δb的论域可以得到Uij的具体值,以及Uij对应的权重,用Kij表示(即:Ei和Ecj隶属度的乘积).最终得到首舵角的输出值为
(5)
尾舵控制纵倾的模糊控制规则类似,不再赘述.
3 潜艇运动控制仿真分析
3.1 静水条件下,垂直面变深运动仿真
补充均衡完毕的潜艇,不考虑外界干扰力和力矩的作用,在静水中由水下30 m潜至水下60 m,仿真结果见图1~2.由仿真结果可知,在无外界干扰的情况下,均衡好的潜艇,PID控制和模糊控制都能很好的实现潜艇变深,从操舵曲线来看,两种方法的操舵规律相近.
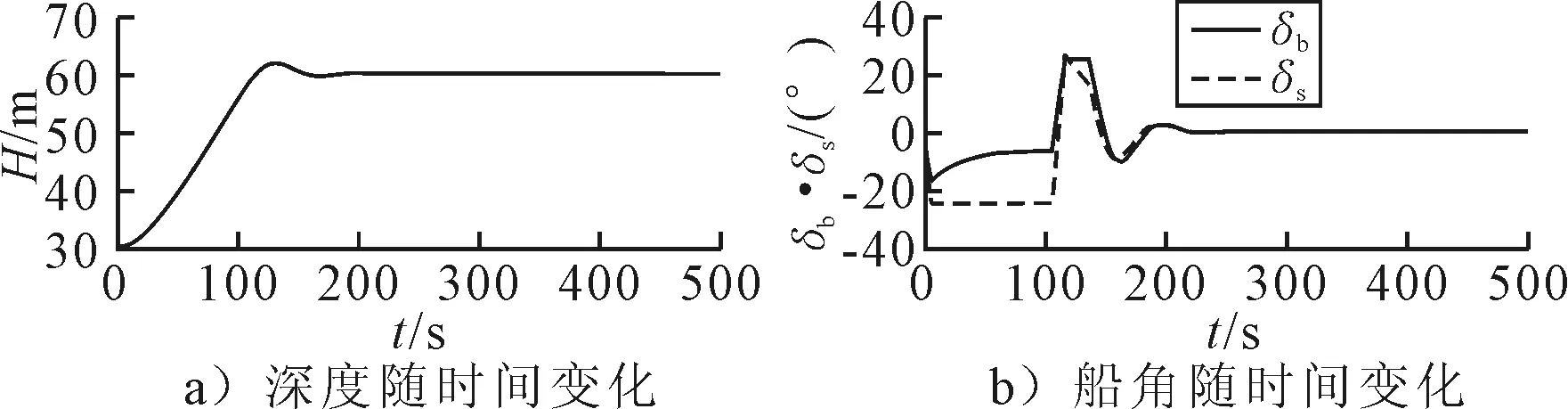
图1 无干扰条件,PID控制器变深结果
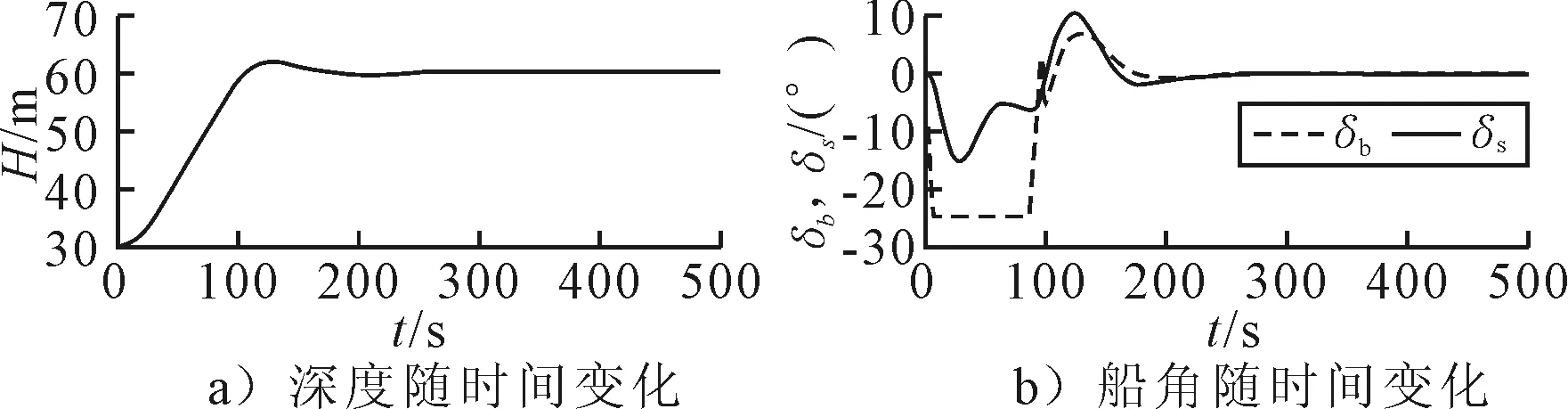
图2 无干扰条件,模糊控制器变深仿真结果
3.2 外界干扰条件下,定深运动仿真

图3 有干扰条件,PID控制器定深控制结果

图4 有干扰条件,模糊控制器定深控制结果
由仿真结果可知,在有干扰条件下的定深控制,两种定深控制效果相近,模糊控制收敛速度略好一些.但是从转舵幅度和频率上来看,模糊控制的效果要远好于常规的PID控制.这是由于PID控制算法本身对误差的相应很灵敏,因此会出现操舵频率高而且频繁操极限舵角的现象,这样对舵机的损害是较大的.模糊控制能用较小的操舵幅度来精确的控制潜艇定深航行,操舵曲线平滑,可操作性强.
从模糊控制的原理上分析,控制器的输入为误差和误差的变化率,相当于PD控制,缺点就是“零输入时,零输出”.因此上述的模糊控制器也存在控制死区.当要求潜艇以某一恒定的纵倾角定深或变深运动时,上述的模糊控制器是无能为力的,因为均衡好的潜艇平衡纵倾角为零,因此上述控制器可以控制潜艇保持无纵倾角定深航行,而无法实现潜艇有纵倾定深航行或不均衡条件下的定深航行[9-11].
4 模糊控制器的改进


表2 尾舵控制纵倾角的模糊控制积分环节
加入积分环节后,模糊控制器输出舵角值为:原模糊控制器输出加上积分环节输出的值.因此积分环节的输出舵角值的论域不能过大,否则会出现饱和现象,经反复试验,取首舵模糊积分环节Δδb的论域为{-0.06,-0.04,-0.02,0,0.02,0.04,0.06},尾舵模糊积分环节Δδs的论域为{-0.003,-0.002,-0.001,0,0.001,0.002,0.003}.
无外界干扰条件下,利用改进的模糊控制器对潜艇以3°首纵倾角,由30 m变深至60 m,运动进行控制.并用原模糊控制器结果进行对比,结果见图5~6.

图5 无干扰条件,无模糊积分仿真结果
在有随机持续波浪力的干扰条件下,以3°首纵倾角,由30 m变深至60 m,运动进行控制,结果见图7~8.

图8 干扰条件,加入模糊积分结果
由仿真结果可知,无模糊积分环节的控制器无法使潜艇在变深过程中达到预期的纵倾角,存在明显的静差,而且由于纵倾不为零产生的不均衡量,使得深度亦不能达到预期的深度,深度也存在明显的静差,见图5和图7.在深度(首舵)和纵倾(尾舵)控制中加入模糊积分环节后,可有效消除模糊控制器的静差,使潜艇保持3°首纵倾角做变深运动,见图6和图8.
5 结 束 语
本文设计的一种适用于潜艇垂直面运动的模糊控制器,能够更好的适应潜艇在有持续随机外界扰动条件下的控制,而且操舵曲线比较平滑,具有较好的可操作性.另外,通过加入模糊积分环节,有效的解决了传统模糊控制存在控制死区的问题,能够使潜艇在存在不均衡量和持续外界干扰的条件下,按照预期的深度和纵倾角定深航行.
参考文献
[1] 杨盐生,于晓莉,贾欣乐.船舶航向鲁棒PID自动舵设计[J].大连海事大学学报,1999(25):11-15.
[2] 张显库,郭晨,杨盐生.两种非线性鲁棒PID控制器[J].黑龙江大学自然科学学报,2005(22):606-609.
[3] 刘健,林莉,郭亦平,等.潜艇垂直面运动的鲁棒控制[J].舰船科学技术,2011(33):32-36.
[4] 赵阳,邢继峰.潜艇垂直面运动自适应神经网络模糊控制仿真[J].计算机仿真,2009(26):26-29.
[5] 胡坤,吴超.潜艇深度模糊控制及仿真研究[J].系统仿真学报,2004(16):2364-2366.
[6] 梁海军,闫超.环境干扰力作用下船舶操纵运动仿真数学模型研究[J].舰船科学技术,2015(37):153-156.
[7] 刘可峰,连琏,姚宝恒.潜艇低速运动时操纵控制仿真[J].舰船科学技术,2014,36(11):19-22.
[8] XIONG H Y,WU G J. Unsteady analysis of six-DOF motion of a 6:1 prolate spheroid in viscous fluid[J]. Science China Physics, Mechanics & Astronomy,2017(60): 1-16.
[9] 高峻吉,黄昆仑,朱军.潜艇定深运动的自适应模糊控制研究[J].海军工程大学学报,2004(16):83-88.
[10] 彭利坤,吕帮俊,陈佳.潜艇操纵[M].武汉:海军工程大学出版社,2016.
[11] CHEN C W, KOUH J S, TSAI J S. Maneuvering modeling and simulation of auv dynamic systems with euler-rodriguez quaternion method[J]. China Ocean Eng,2013(27):403-416.

