基于刚柔耦合模型轮轨两点接触的动力学仿真

姚永明，李国芳，丁旺才

(兰州交通大学 机电工程学院，甘肃 兰州 730070)

0 引言

随着我国高速动车组运行速度的不断提高，轮轨关系问题变得很突出，轮轨接触越来越复杂，轮轨相互作用加强，导致轮轨磨耗加剧，车轮踏面损伤日益严重，这必然会改变轮轨间接触几何关系。由此产生不同的轮轨力，直接影响列车的运行平稳性、安全性及其运输成本，因此对轮轨关系进行深入全面的研究有重要意义。

E. Meil[1]运用有限元理论，将车轮和轨道分别离散成弹性可变形的体，根据Navier公式和解析接触条件建立稀疏力学方程来求解接触点。张卫华[2]结合机车车辆在滚动台上的试验情况，应用迹轨线法，提出在空间状态下轮轨接触点的计算方法。任尊松[3-5]在迹线极值法的基础上研究了轮轨接触几何关系，推导出了轮轨多点接触的计算与判定方法。宋华[6]考虑缓和曲线、车轮踏面、轨下弹性支撑和悬挂系统以及列车牵引力的影响，建立了非线性稳态曲线通过轮轨滚动接触的有限元模型，研究了列车通过非线性稳态曲线线路时的轮轨滚动接触问题。陶功权、金学松[7]等人分别采用三维弹性体非Hertz滚动接触理论和三维轮轨接触有限元模型计算了轮轨接触斑面积、接触压力和接触应力等。然而刚柔耦合的两点接触研究甚少。

本文基于多体动力学软件UM建立了某型车的刚柔耦合动力学模型，将构架考虑成弹性体，研究了该动力学模型通过小曲线半径时单点接触和两点接触模型的动力学指标差异。

1 模型建立与轨道设置

1.1 柔性构架的建立与求解过程

通过有限元分析软件ANSYS和多体动力学软件UM(universal mechianism)的接口模块UM FEM建立弹性构架的模型。具体建模步骤如下：

1) 将构架的三维几何模型导入有限元软件ANSYS并根据构架的几何特性及力学特性获得其有限元模型；

2) 选择弹性构架接口节点，根据Craig-Bampton法计算构架的固有模态和静模态，输出4个标准输出文件*.rst，*.full，*.free，和*.mlmp；

3) 在ANSYS_UM中将数据转换成UM读取的格式*.fss或者*.fum；

4) 最后将得到的*.fss导入UM Input中转换成柔性体子结构。如图1所示。

图1 构架弹性化处理过程

1.2 建立动力学模型

该车辆系统具有两系悬挂，刚柔耦合模型具有15个体(1个车体、2个构架、4个轮对、8个转臂轴箱)，具体物理量参数如表1所示，其中将构架考虑成弹性体，车体和转向架之间的连接弹簧和阻尼器等看作是无质量的连接单元。该车辆系统动力学模型如图2所示，刚柔耦合模型如图3所示。

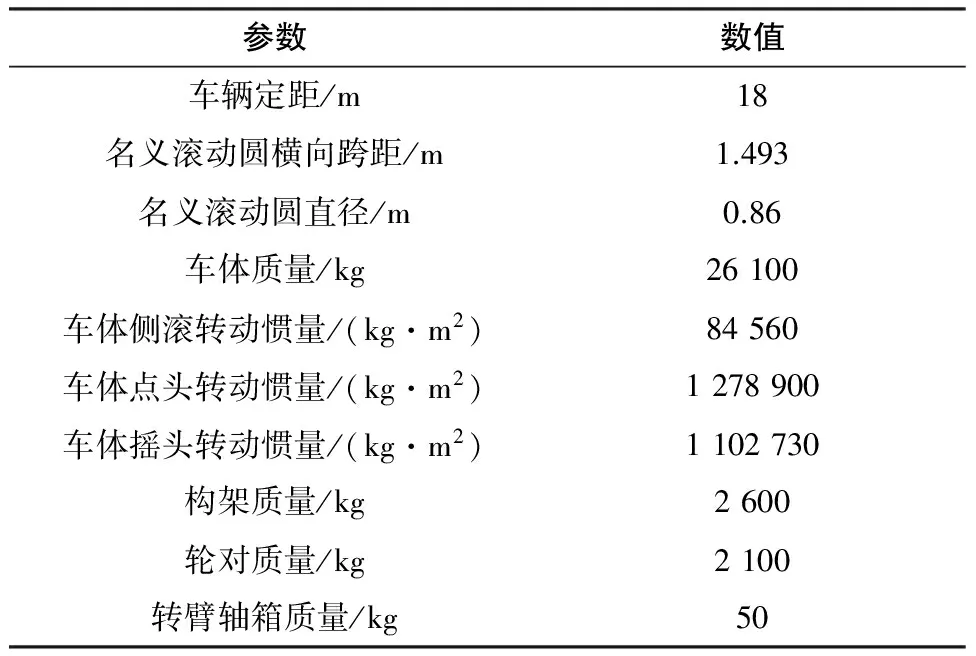
表1 车辆系统主要参数

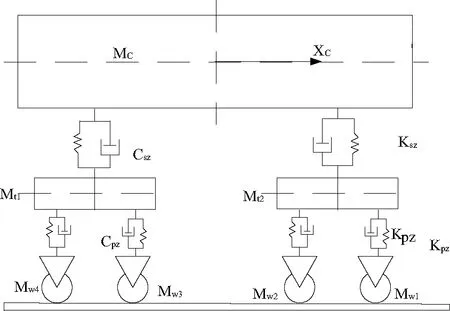
图2 动力学计算模型

图3 整车动力学模型

1.3 轮轨型面和线路设置

该模型的轮对采用LMA型磨耗型踏面，钢轨采用CHN60钢轨，轨底坡为1/40。UIC_good轨道谱作为轨道激励输入，UIC谱左右轨的水平和高低不平顺幅值变化关系如图4所示。

图4 UIC_good轨道谱

曲线路段由两端的进出直线和缓和曲线、圆曲线及轨道不平顺组成，曲线线路示意图如图5所示，具体设置为直线(50 m)-缓和曲线(350 m)-圆曲线(200 m)-缓和曲线(350 m)-直线(50 m)，外轨超高150 mm。

图5 曲线线路示意图

2 曲线通过分析

轮轨间存在非常复杂的接触和约束关系，表现在轮轨接触斑内存在高接触应力[8]。总体上看，轮轨接触大致可分为法向和切向两类，法向问题主要涉及赫兹接触理论，切向问题主要涉及Kalker蠕滑理论[9]。

车轮和钢轨之间的接触状态可能有两种[10]，即单点接触和两点接触。轮对和钢轨的相对移动量和摇头角不大时，车轮踏面与钢轨顶面相接触，发生单点接触；如果轮对和钢轨的相对移动量和摇头角超过一定范围，就可能会引起车轮踏面、轮缘同时与钢轨顶面、侧面相接触，发生两点接触。轮对在曲线轨道上运行时的受力如图6和图7所示。图6是轮轨间单点接触的情况；图7是轮轨间两点接触的情况。

2.1 单点接触

假设车辆在曲线通过时，车轮和钢轨单点接触(受力情况如图6所示),可得：

mwaw=Tl+Tr+TNl+TNr+Fsw+Fw

(1)

图6 车辆在曲线上轮对受力分析

2.2 两点接触

根据图7曲线通过时外轮发生两点接触时的受力情况，可以推导出前后轮对的6个方程[11]，下标t、F分别表示踏面、轮缘上的作用力[10]。

图7 车辆在曲线上轮对受力分析

纵向运动：

(2)

横向运动：

(3)

垂向运动：

(4)

侧滚运动：

a(Tzr+TNzr)+rr(Tyr+TNyr-ψWTxr)+Msxw+ψw(Mylt+MylF+Myr)

(5)

点头运动：

rlF(Txlt+ψwTylt)-rlF(TxlF+ψwTylF)-rr(Txr+ψwTyr)+Td

(6)

摇头运动：

(7)

3 曲线通过时的轮轨接触关系

为使得轮轨间能够发生两点接触，这里设置极端工况：车辆以100km/h速度通过曲线半径R=400m的小半径曲线。车轮与钢轨不仅发生踏面接触，还将发生轮缘接触。

图8给出在上述工况下，采用单点接触模型和两点接触模型时轮轨接触角和接触斑处的法向力的对比。从图中可以看出，在直线段运行时，采用单点接触和两点接触模型，踏面上的接触角和法向力几乎保持一致，并且两点接触模型的第二个接触点上的接触角和法向力的数值为0。当车辆系统运行到曲线段时，两点接触模型的第二个接触点的接触角和法向力的数值发生了变化，说明轮轨之间发生了两点接触，并且第一个接触点上的接触角和法向力均大于第二个接触点。

当车辆运行速度较小，曲线半径足够大时，车轮与钢轨之间仅发生踏面接触。这里设置了轮轨之间仅发生踏面接触的工况：车辆以100km/h的速度通过曲线半径R=2 000m的曲线。由图9可以看出随着车辆的运行，两点接触模型的第二个接触点的接触角和法向力的数值始终为0，说明车轮和钢轨之间仅发生了单点接触，并且两种接触力模型的轮轨接触角和法向力的数值基本保持一致。

图8 单点接触时轮轨接触角和法向力

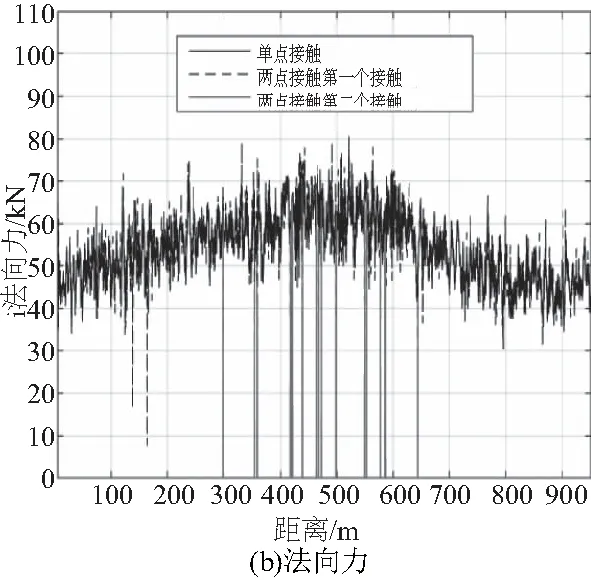
图9 两点接触时轮轨接触角和法向力

表2给出了车辆在不同运行速度和不同曲线半径下运行时，车轮和钢轨之间接触点个数之间的关系。从表中可以看出，轮轨之间接触关系不仅仅与曲线半径有关，还与车辆运行的速度有着很大的关系。曲线半径越小，车辆运行速度越大，车轮和钢轨之间越容易发生两点接触。

表2 不同速度、不同曲线半径下轮轨接触点个数 V/(Rm/h)

4 动力学仿真

4.1 最大横向位移影响

图10为轮轨单点接触模型和两点接触模型在不同速度和曲线半径下1位轮对的最大横向位移图。从图中可以看出列车运行速度越快，曲率半径越小，1位轮对的横向位移越大。曲线半径越小，速度对1位横向位移的影响越大；曲线半径越大，速度对1位轮对横向位移影响越小。

表3给出了，在同一半径下，车辆运行速度从60km/h提升到120km/h时，1位轮对横向位移的增长率。由表3可以看出，随着曲线半径的增加，1位轮对的最大横向位移随速度的增长率不断减小；曲线半径增加到1 000m后，1位轮对最大横向位移随速度的增长率将保持在3%左右；曲线半径在400～1 200m时，两点接触模型的1位轮对最大横向位移随速度的增长率小于单点接触模型；曲线半径在1 400～2 000m时，两点接触模型的1位轮对最大横向位移随速度的增长率略大于单点接触模型。

表3 不同接触方式、不同曲线半径下1位轮对横向位移随速度的增长率

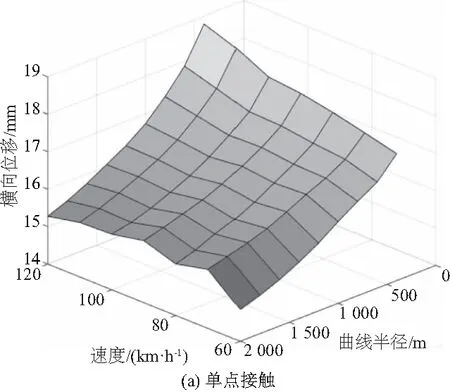
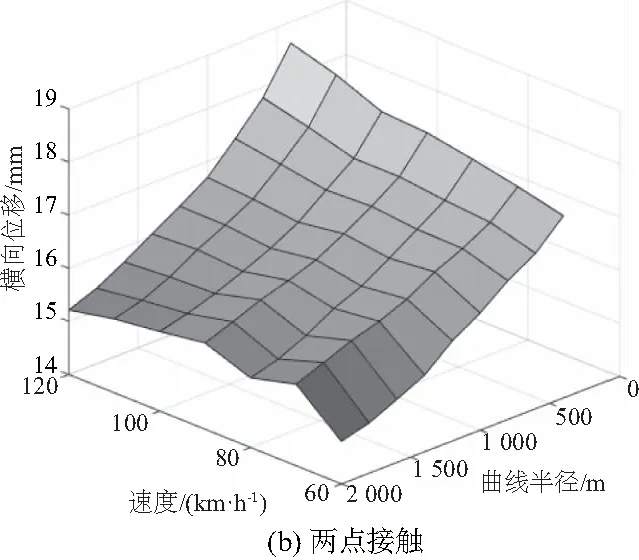
图10 速度和曲线半径对横向位移的影响

4.2 接触角影响

图11为轮轨单点接触模型和多点接触模型在不同速度和曲线半径下1位轮对的接触角图。从图中可以看出，列车运行速度越快，曲率半径越小，1位轮对的接触角越大。曲线半径越小，速度对1位轮对接触角的影响越大；曲线半径越大，速度对1位轮对接触角影响越小。

对比图11(a)和图11(b)可以看出，曲线通过时两点接触模型的接触角略大于单点接触模型；两点接触模型速度-曲线半径-接触角的曲面图的明显光滑度比较差。

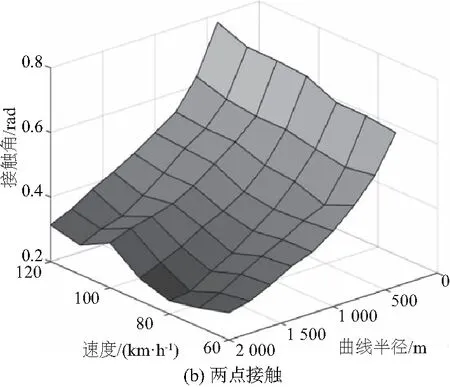
图11 速度和曲线半径对接触角的影响

表4给出了，在同一半径下，车辆运行速度从60km/h提升到120km/h时，1位轮对轮轨接触角的增长率。由表4可以看出，曲线半径的增加对1位轮对的接触角随速度的增长率影响不是很大；1位轮对接触角随速度的增长率保持在15%左右；曲线半径在400～800m时，单点接触模型的1位轮对接触随速度的增长率大于两点接触模型；曲线半径在1 000～2 000m时，两点接触模型的1位轮对接触角随速度的增长率大于单点接触模型。

表4 不同接触方式、不同曲线半径下1位轮对接触角随速度的增长率

4.3 横向力影响

图12为轮轨单点接触模型和两点接触模型在不同速度和曲线半径下1位轮对的横向力图。从图中可以看出，列车运行速度越快，曲率半径越小，1位轮对的横向力越大。曲线半径越小，速度对1位轮对横向力的影响越大；曲线半径越大，速度对1位轮对横向力影响越小。

从图12(a)可以看出，当列车以160 km/h速度通过曲线半径为400 m的上述曲线时，单点接触模型的1位轮对的最大横向力达到111 040 N；从图12(b)可以看出，当列车以160 km/h速度通过曲线半径为400 m的上述曲线时，两点接触模型的1位轮对的最大横向力为57 368 N。对比图12(a)和图12(b)可以看出，曲线通过时两点接触模型的1为轮对横向力明显小于单点接触模型；两点接触模型速度-曲线半径-横向力的曲面图的光滑度略差于单点接触模型。

表5给出了在同一半径下，车辆运行速度从60 km/h提升到120 km/h时，1位轮对横向力的增长率。由表5可以看出，随着曲线半径的增加，1位轮对的横向力随速度的增长率不断减小；单点接触模型的1位轮对横向力随速度的增长率明显小于两点接触模型，但是两者之间的差距随着曲线半径的增大而缩小。

表5 不同接触方式、不同曲线半径下1位轮对横向力随速度的增长率

图12 速度和曲线半径对横向力的影响

4.4 垂向力影响

图13为轮轨单点接触模型和两点接触模型在不同速度和曲线半径下1位轮对的垂向力图。从图中可以看出，列车运行速度越快，曲率半径越小，1位轮对的垂向力越大。曲线半径越小，速度对1位垂向力的影响越大；曲线半径越大，速度对1位轮对垂向力影响越小。

对比图13(a)和图13(b)可以看出，曲线通过时两点接触模型的垂向力略大于单点接触模型；两点接触模型速度-曲线半径-横向力的曲面图的明显光滑度比较差。

表6给出了，在同一半径下，车辆运行速度从60 km/h提升到120 km/h时，1位轮对垂向力的增长率。由表6可以看出，随着曲线半径的增加，1位轮对的垂向力随速度的增长率不断减小；曲线半径增加到1 000 m后，1位轮对横向位移随速度的增长率将保持在10%左右；单点接触模型1位轮对垂向力随速度的增长率大于两点接触模型，但是两者之间的差距随着曲线半径的增大而缩小。

4.5 脱轨系数影响

图14为轮轨单点接触模型和两点接触模型在不同速度和曲线半径下1位轮对的脱轨系数图。从图中可以看出，列车运行速度越快，曲率半径越小，1位轮对的脱轨系数越大。曲线半径越小，速度对1位轮对脱轨系数的影响越大；曲线半径越大，速度对1位轮对脱轨系数影响越小。

表6 不同接触方式、不同曲线半径下1位轮对垂向力随速度的增长率

图13 速度和曲线半径对垂向力的影响

对比图14(a)和图14(b)可以看出，单点接触模型和两点接触模型通过曲线半径为400～1 400m的曲线时，1位轮对的脱轨系数基本重合；两点接触模型速度-曲线半径-横向力的曲面图的明显光滑度比较差。

表7给出了，在同一半径下，车辆运行速度从60km/h提升到120km/h时，1位轮对脱轨系数的增长率。由表7可以看出，曲线半径从400m增加到600m时，单点接触模型1位轮对的脱轨系数随速度的增长率不断减小；曲线半径增加到1 400m后，1位轮对横向位移随速度的增长开始速增大；随着曲线半径的增加，两点接触模型的1位轮对脱轨系数随速度的增长率先减小后增大，最后出现了负增长。两点接触模型的1位轮对脱轨系数随速度的增长率基本都小于单点接触模型。

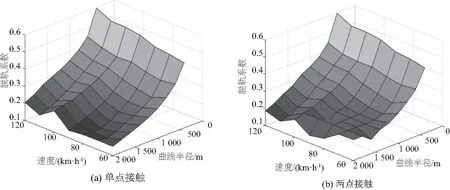
图14 速度和曲线半径对脱轨系数的影响

表7 不同接触方式、不同曲线半径下1位轮对脱轨系数随速度的增长率

5 结语

基于多体动力学软件UM建立了某型车的单点接触和两点接触的刚柔耦合动力学模型。对两种动力学车辆系统在曲线通过时进行了动力学仿真，得到以下结论：

1) 车辆运行速度越快、曲率半径越小，1位轮对的横向位移、接触角、横向力、垂向力、脱轨系数等动力学指标影响越大。

2)曲线半径越小，速度对1位轮对的各项动力学指标的影响越大；曲线半径越大，速度对1位轮对的各项动力学指标影响越小。

3) 曲线半径在400～1 000 m时，两点接触模型的1位轮对最大横向位移、接触角、垂向力、脱轨系数等动力学指标随速度的增长率大于单点接触模型；曲线半径在1 200～2 000 m时，两点接触模型的1位轮对最大横向位移、接触角、垂向力、脱轨系数等动力学指标随速度的增长率小于单点接触模型。因此研究车辆系统在曲线通过的轮对最大横向位移、接触角、垂向力、脱轨系数等动力学指标时，当曲线半径在400～1 000 m时，建议采用两点接触模型，当曲线半径>1 000 m时可采用单点接触模型。

4) 曲线通过时单点接触模型的1位轮对横向力远远大于两点接触模型；但单点接触模型的1位轮对横向力随速度的增长率明显小于两点接触模型，但是两者之间的差距随着曲线半径的增大而缩小。因此研究车辆系统在曲线通过时的轮对横向力，建议采用两点接触模型。

[1] E. Meil, S. Magheri, M, Malvezzi. Development and implementation of a differential elastic wheel-rail contact model for multibody applications [J]. Vehicle System Dynamics, 2001,49(6): 969-1001.

[2] 张卫华. 空间状态轮轮(轨)接触点计算方法[J]. 中国铁道科学,2006,27(4): 76-79.

[3] 任尊松,孙守光. 道岔区轮轨接触几何关系研究[J]. 工程力学,2008,25(11): 223-230.

[4] 任尊松,金学松. 轮轨多点接触计算新方法曲线通过验证[J]. 机械工程学报,2010,46(16):2-7.

[5] 任尊松. 轮轨多点接触计算方法研究[J]. 铁道学报,2011,33(3):25-30.

[6] 宋华,杨建,张月,宋林邦,等. 非线性稳态曲线通过时轮轨滚动接触的数值求解方法[J]. 中国铁道科学,2015,6(5):80-86.

[7] 陶功权,李霞,温泽峰,等. 两种轮轨接触应力算法对比分析[J]. 工程力学，2013,30(8):229-235.

[8] Iwnicki S. Handbook of Railway Vehicle Dynamics[M]. London: CRC Taylor & Francis Group, 2006.

[9] 任尊松. 轮轨多点接触及车辆-道岔系统动态相互作用[M]. 北京:科学出版社,2014.

[10] 张卫华. 机车车辆动态模拟[M]. 北京:中国铁道出版社,2007.

[11] 姚建伟,孙丽霞. 机车车辆动力学[M]. 北京:科学出版社,2014.