薄壁盒形件真空吸附装夹变形的计算方法研究

李勇，江磊，马术文，刘蕾，陈雪梅

(1. 西南交通大学 机械工程学院，四川 成都 610031； 2. 成都飞机工业(集团)有限责任公司 制造工程部，四川 成都 610092 )

0 引言

薄壁类零件由于刚度较差，在装夹时容易产生变形。装夹变形是加工误差的主要来源，最终会影响零件的加工精度，严重者会引起加工缺陷，导致零件报废。因此，研究薄壁类零件的装夹变形和优化装夹方案对控制和提高加工精度具有重要的意义。为了减小装夹变形对薄壁件精度的影响，提高其加工质量，众多研究者主要从装夹变形预测、控制，装夹方案优化，装夹方式的选择等方面做了大量的研究。秦国华等针对薄壁件的装夹布局方案，利用有限元方法获取神经网络训练样本，提出了基于神经网络与遗传算法的装夹变形“分析-预测-控制”方法[1-2]。于金等利用有限元模拟了薄壁框体类零件在铣削加工中不同装夹位置的变形，得出了最终的优化装夹布局方案，并做了相关的验证试验[3]。王军等借助数值模拟方法对铝合金薄壁壳体件装夹方案进行了优选，分析了在集中载荷与均布载荷作用下，装夹位置、装夹顺序及加载方式对其变形的影响[4]。董跃辉等通过有限元软件，研究了装夹位置、顺序及夹紧力加载方式等因素对薄壁框体零件变形的影响[5]。许晓宇等通过遗传算法与有限元方法，提出了夹紧顺序、装夹布局与夹紧力同步优化的分析方法[6]。Asante提出了通过工件几何与定位误差、装夹变形等分析加工精度的模型[7]。

目前，在加工薄壁件时多采用吸附方式，其夹紧力较小但吸附面积较大，通常能产生较大的摩擦力使工件固定，吸附方式主要分为磁力吸附和真空吸附[8]。试验研究表明，对薄壁件采用真空吸附装夹时的加工精度要明显高于采用传统装夹方式[9]。上述文献多是针对结构简单的薄板或框类零件在传统装夹方式下的装夹变形分析与装夹方案优化，本文以薄壁盒形零件为例，通过理论计算与有限元方法研究其在真空吸附下的几种变形情况。

盒形件结构特征是中间凸起形成一盒状、整个结构长宽尺寸较大，因此不能采用传统的装夹方式，可采用真空吸附的方式进行装夹。然而，盒形件在制造过程中易出现误差，一旦盒形件各面与夹具托盘各面之间不能较好地贴合就会产生较大的装夹变形，进而对加工精度会产生不同的影响，因此有必要对其装夹变形进行分析，进而找出较好的变形控制方法，提高加工精度。

1 装夹变形量的理论计算

图1(a)为某典型盒形件的三维模型，其壁厚3mm。定义A、C为两侧面，B为顶面，D为底部轮廓上表面。图1(b)为盒形件装夹示意图，工件、密封圈与夹具定位面形成密闭腔，在夹具托盘顶面有一个与真空发生装置相通的抽真空气孔。抽真空后，密闭腔产生一定的负压，从而使盒形件顶面及侧壁与夹具托盘紧密贴合，最终使工件夹紧。

设H为密封圈超出密封槽的高度值，L、L'分别为夹具托盘截面顶部和盒形件顶面宽度，L1、L2分别为盒形件左右两侧壁宽度，α1、α2分别为夹具托盘左右两侧面与顶面所成夹角，θ1、θ2分别表示盒形件左右两侧壁与顶面所成夹角。

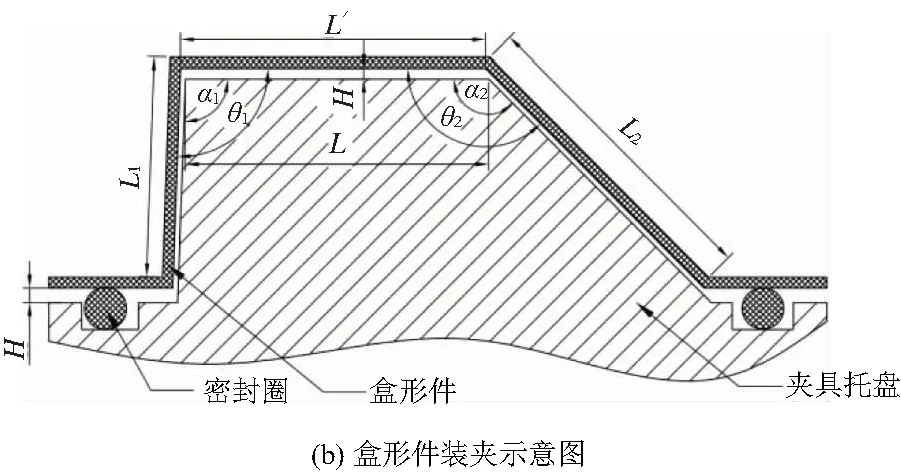
图1 盒形件三维模型与装夹示意图

图2表示理想情况下盒形件装夹几何关系，在盒形件截面上选取a、b、c、d4个计算点研究其在装夹过程中发生的位移变形，夹具截面上与之对应的点为a1、b1、c1、d1。设δ1、δ2、δ3、δ4分别表示c、a、d、b沿水平方向的位移变形。假设夹具不存在变形，根据盒形件与托盘的尺寸组合关系，在装夹过程中最容易使盒形件产生变形的几何误差类型有4种，如表1所示。

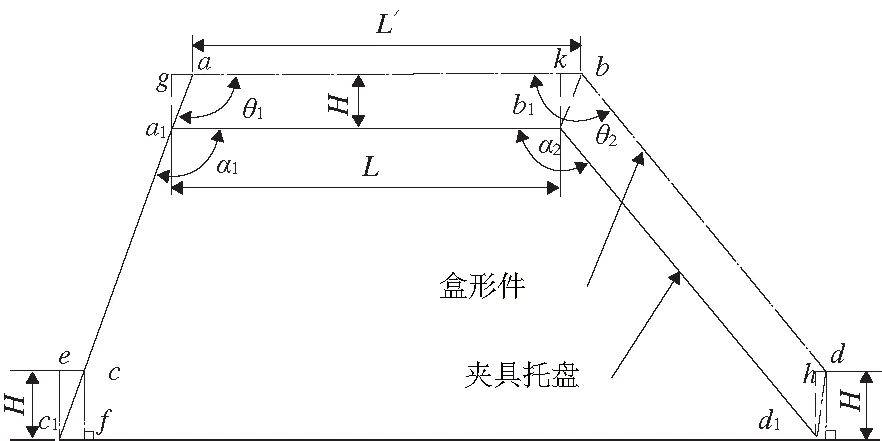
图2 理想情况下盒形件装夹几何关系

设Δi表示各误差类型下各计算点的总的位移变形，ΔA、ΔB、ΔC分别表示A、B、C面的最大位移变形量，则有式(1)、式(2)：

表1 盒形件几何误差类型

(1)

(2)

根据上述分析，提出了以下盒形件各面变形量的计算方法，并利用装夹过程中盒形件与夹具几何关系的变化推导了相应的变形计算公式。

1.1 类型1

如图3所示，设g点为a点发生水平位移变形后位置，k点为b点发生水平位移变形后位置，h为夹具截面左侧面上延长线与工件顶部的交点。由于θ1和θ2均偏小，故而产生误差角度β1、β2，在施加载荷后，工件在与托盘贴合的过程中克服已存在的误差而发生变形。以c点为例，其最后应与c1重合，因此在施加载荷后在水平方向上的位移变形为δ1=|c1f|。

图3 类型1几何模型(θ1<α1，θ2<α2，L'=L)

对a点，理想情况是其最终与a1重合，因此在吸附力及夹具反力作用下在水平方向上发生的位移为δ2=|ag|，同理，在载荷作用下b点发生的水平位移为δ4=|bk|，d点水平位移是δ3=|e1d1|，且根据图3中的几何关系有：

δ1=|c1f|=|gh|=Htan(α1-90°)

(3)

δ2=|ag|=|ah|-|gh|

(4)

δ3=|e1d1|=Htan(α2-90°)

(5)

δ4=|bk|

根据相似三角形原理，有：

其中：|ac|=L1，则可求得：

代入式(4)则有：

δ2=L1[tan(α1-90°)-tan(θ1-90°)]·cos(α1-90°)-Htan(α1-90°)。

(6)

由三角形全等知|ag|=|bk|，故有：

δ4=δ2

(7)

1.2 类型2

如图4所示，当θ1>α1，θ2>α2时，在装夹过程中，根据定位基准面(左侧面)找正装夹，但因存在角度误差，故会形成定位面与基准不完全重合现象，根据几何关系可知|ag|=|bk|，且可得以下各式：

图4 类型2几何模型(θ1>α1，θ2>α2， L'=L)δ1=|cf|-|ef|

(8)

δ2=δ4=|ag|=Htan(θ1-90°)

(9)

δ3=|kb2|=δ4+|bb2|

(10)

|a1c|=L1-|aa1|

|ef|=Htan(α1-90°)

又根据正弦定理有：

求得：

(11)

(12)

1.3 类型3

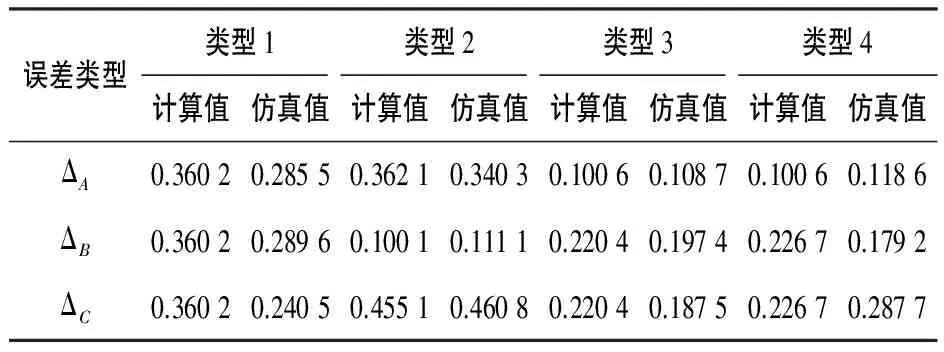
如图5所示，当L'

图5 类型3几何模型(θ1=α1，θ2=α2 ，L'

(13)

δ2=|ag|=H'tan(α1-90°)

(14)

δ4=|bk|=L-L'-δ2=ΔL-δ2=H'tan(α2-90°)

(15)

δ3=|dh|

由式(14)、式(15)可知：

当L'越小时，ΔL越大，为了使工件能与定位面完全贴合，则工件顶面距托盘顶部的距离H'会越大，根据工件误差要求，L'与L相差不能太大，因此为了计算方便，可令H'=H，则：

δ1=δ2=Htan(α1-90°)

(16)

根据几何关系推导知，|bk|=|dh|，故有：

δ3=δ4=ΔL-δ2

(17)

1.4 类型4

由图6可知，类型4的计算方法与类型3的相似，若令H'=H，根据几何关系有：

图6 类型4几何模型(L'>L，θ1=α1，θ2=α2)δ1=|ce|=Htan(α1-90°)

(18)

δ2=|ag|=Htan(α1-90°)

(19)

δ4=|bk|=L'-L+δ2=ΔL+δ2

(20)

δ3=|dh|=|bk|=ΔL+δ2

(21)

2 装夹变形有限元仿真计算

本文采用ANSYS Workbench软件，对盒形件的装夹变形进行仿真计算。首先根据所示的几何参数建立4种误差类型下的仿真三维模型，在ANSYS Workbench中进行网格划分，最后采用接触分析来模拟真空吸附夹紧过程，下面针对主要的分析过程进行说明。

2.1 定义材料

铝合金盒形件与夹具托盘材料属性如表2所示，在ANSYS Workbench中按照表中数据定义材料即可。

表2 材料参数

2.2 接触设置

接触设置主要包括接触面与目标面的选取、接触刚度的选择、接触类型及接触算法的选择。

接触分析属于非线性问题，ANSYS中接触一般分为两大类：刚性到柔性接触类、柔性到柔性接触类，盒形件接触属于柔性到柔性接触。在接触分析中需要选择恰当的接触面和目标面，一般在柔性到柔性接触中选刚度较大的面作为目标面，因此选夹具面为目标面，盒形件各面为接触面建立接触。

接触刚度设置越大，接触穿透就越小，精度越高，但大的接触刚度会造成收敛困难，ANSYS接触刚度系数一般在0.01～10之间变化。为确定合适的接触刚度系数，应从较低值开始，不断增大进行多次试算，直到接触应力变化较小为止。为了节约时间，本次分析根据其他文献的类似分析，直接选取接触刚度系数为2。

在真空吸附夹紧时，盒形件各面会与相应的夹具面贴合，本文据此共建立6对接触，如图7所示，接触类型为无摩擦接触。

图7 盒形件接触设置

2.3 网格划分

为使分析结果更加可靠，在网格划分时先对模型进行较为精细的全局网格划分，然后利用接触面尺寸控制进行局部网格的细化，目的是使接触区域产生一致的网格，从而使计算更加准确。

2.4 施加约束与载荷

根据实际装夹过程，在夹具底面与侧面施加固定约束，在盒形件各接触面上沿其法线方向施加面载荷，大小为开真空后产生的负压值。在上表面施加一个位移约束，其值为密封圈超出密封槽的高度H，如图8所示。

图8 施加载荷与约束

3 实例验证

表3为4种误差类型下盒形件的几何参数，根据所列几何参数分别采用理论和仿真方法进行了装夹变形的计算，其结果如表4所示，仿真计算变形云图如图9所示。

表3 盒形件计算几何参数 mm

表4 变形理论计算和仿真计算值 mm

图9 类型1变形云图

从表4和图10可知，变形量的理论和仿真计算值吻合度较好，验证了两种计算方法的可行性，可根据计算条件进行方法的选择。

图10 变形量理论计算值和仿真计算值曲线图

通过对盒形件装夹变形量的计算，可知误差类型1和类型2对盒形件装夹变形影响较大，且误差角和偏差ΔL越大，变形量也越大。因此装夹时应严格控制盒形件两侧面与夹具托盘侧壁之间的角度误差和宽度方向的偏差ΔL。

4 结语

以薄壁盒形件为研究对象，通过理论计算与有限元仿真两种方法，提出了薄壁盒形件在真空吸附装夹方式下的装夹变形计算流程，并通过实例对两种方法进行了验证，为薄壁盒形件的变形和装夹误差计算提供了有效的计算方法。

[1] 秦国华,赵旭亮,吴竹溪. 基于神经网络与遗传算法的薄壁件多重装夹布局优化 [J]. 机械工程学报,2015,51(1):203-212.

[2] 秦国华,吴竹溪,张卫红. 薄壁件的装夹变形机理分析与控制技术[J]. 机械工程学报,2007,43(4):211-216.

[3] 于金,刘成林,朱秀峰,等. 薄壁件装夹位置优选有限元分析与实验研究[J]. 航空精密制造技术,2013,49(6):30-32.

[4] 王军,耿世民,张辽远,等. 薄壁壳体件装夹变形机理有限元分析与控制[J]. 兵工学报,2011,32(8):1008-1013.

[5] 董跃辉,柯映林. 铣削加工中薄壁件装夹方案优选的有限元模拟[J]. 浙江大学学报,2004,38(1):17-21.

[6] 许晓宇,赵晓慈. 夹紧顺序、夹具布局和夹紧力对装夹变形影响与同步优化分析研究[J]. 图学学报,2016,37(01):20-24.

[7] Asante, J.N. A small displacement torsor model for tolerance analysis in a workpiece-fixture assembly[J]. Journal of Engineering Manufacture,2009,223(8): 1005-1020.

[8] 李昌达,张志盛,王欣. 关于异形薄壁件加工夹具的探讨[J]. 机械工程师, 2014(7):244-245.

[9] 苗广辉,范帆,姜瑞华. 真空吸附在薄板加工中的应用[J]. 制造技术与机床, 2007(1):93-94.

[10] Seghedin, Neculai-Eugen. The tightening accuracy of workpieces in the multiple clamping devices[J]. Academic Journal of Manufacturing Engineering, 2014,12(2):73-78.