响应面和多目标法优化悬架参数的分析

李静，王东方，缪小冬

(南京工业大学 机械与动力工程学院，江苏 南京 211800)

0 引言

汽车的操纵稳定性对汽车高速行驶中的稳定性与安全性，以及汽车的驾乘性都有着显著的影响，而悬架系统特性参数对车辆的操纵稳定性起着重要的作用。在汽车的行驶过程中，悬架特性参数的不确定性不仅影响到汽车的转向性能，还直接影响轮胎的磨损，有可能汽车行驶中产生摆振现象，破坏汽车的操纵稳定性。目前国内外的学者在这个问题上做了一些分析研究。文献[1]在汽车前轮胎磨损和操纵稳定性基础上，利用响应面法建立了二阶车轮定位参数数学近似模型，并进一步参数优化。文献[2]设计了一种基于改进遗传算法NSGA-∏的悬架系统多目标优化策略，实现了平顺性和操纵稳定性的优化。

响应面法是利用较少的试验在小范围内获取比较精确的逼近简单的函数代数关系[3]。而多目标方法就是在可设计选定的区域内寻找一些设计变量实现几个目标的优化[4]。

选取国内某车型的麦弗逊式悬架为研究对象，在ADAMS/CAR建立带有转向系统的仿真分析模型，并在ADAMS/Insight中对悬架特性参数进行灵敏度分析，然后针对灵敏度大的悬架参数采用响应面和多目标方法进行优化求解，最后将所用两种方法求解的最优解以及优化前的参数带回悬架模型中再次进行对比仿真试验分析，表明多目标方法具有较好的优化结果。

1 悬架参数分析

1.1 建立前悬架动力学模型

利用ADAMS/CAR自带标准模板对该结构参数进行重新设置和完善，修改连接点坐标值和转向系统技术参数，建立带有转向系统的前悬架虚拟样机仿真模型，如图1所示。

图1 带有转向系统的前悬架仿真分析模型

1.2 确定优化目标及优化变量

在汽车运行过程中，前轮定位参数的不断变化决定悬架系统特性参数。在激振台架上，进行左右两车轮同向上下跳动量为±50mm(汽车在日常行驶状态下)的运动学仿真试验，仿真试验得到结果见图2所示。

图2 车轮定位参数变化关系曲线

由图2可知，车轮外倾角(Camber Angle)变化范围为-1.76°～0.44°，合理的取值范围为1°～2°。主销后倾角(Caster Angle)变化范围为2.29°～2.97°，合理范围为0°～3°。主销内倾角(Kingpin Inclination Angle)变化范围为8.00°～10.30°，设计理想变化范围为7°～13°。前轮前束角(Toe Angle)变化范围为-1.57°～0.85°，理想的变化范围为0°～-0.5°。数据显示出主销后倾角和主销内倾角变动范围小，车轮外倾角和前轮前束角变动范围比较大，不利于汽车操纵稳定性，需要对悬架特性定位参数作进一步优化设计。

1.3 前轮定位参数灵敏度分析

根据文献[5-6]选取硬点坐标作为因素，采用ADAMS/Insight进行参数灵敏度分析，为了避免分析效率低和工作量大，选用扰动分析法的灵敏度分析计算。

(1)

(2)

式(1)表示设计变量在X点i处的灵敏度大小；式(2)表示优化设计变量在X区间内[ximin,ximax]的灵敏度大小；xi为设计变量。

根据以往的工程经验可直接选取悬架的下摆臂前点、外点、后点、转向横拉杆内连接点、外连接点和减振器下安装点的硬点坐标作为设计变量进行分析。选择最优拉丁超立方设计试验方法，将硬点坐标作为因子输入，以车轮外倾角、主销内倾角、主销后倾角和车轮前束角作为输出，可筛选出灵敏度高的变量，分析结果见图3。

图3 设计硬点坐标对定位参数的影响率

由图3可知，选出6个设计因素是对悬架特性参数影响程度较大的，分别为减振器下安装点硬点坐标y，下摆臂外点硬点坐标z，下摆臂前点硬点坐标z，下摆臂后硬点坐标z，转向横拉杆内连接点硬点坐标z、转向横拉杆外连接点硬点坐标z，并分别记作x1,x2,x3,x4,x5,x6。

2 前悬架响应面优化

2.1 响应面模型的建立及可靠性验证

对前悬架车轮定位参数的每一个优化设计变量进行迭代计算时，每次都调用ADAMS/Insight仿真模型进行求解计算，而且设计因素与响应值之间是比较复杂地映射关系。为了提高优化效率和精度，要进行试验设计拟合成二阶响应面近似数学模型，可拟合出包含交互作用项的统计回归模型来逼近悬架模型，数学多项式表达见式(3)：

(3)

式中：yi为仿真分析各响应输出值；α0为常数项待定系数；αi为一次项待定系数；αij为二次项待定系数；xi,xj为筛选出灵敏度高的硬点坐标值，i、j=0,1,…,6。

经过ADAMS/Insight运算可拟合出相应的结果数据，如图4所示。由图4可以看出横坐标与纵坐标呈线性关系，因此可以认定响应面近似模型足以模拟实际悬架模型的可靠性[7]，可以用于后续进一步优化设计。

图4 连接点坐标Y和车轮定位参数关系

2.2 响应面优化模型的求解

在MATLAB中编写出最优值搜索程序，该程序可模拟调整硬点坐标值大小的过程，使用if函数判断语句，条件是根据车轮定位参数零点处的斜率约束优化响应值范围的约束，编写程序如下所示：

y1=-0.000 088 666x1+0.000 17x2-0.000 114 56x3+0.000 235 47x4-0.000 453 2x5+0.000 04x6-0.024 6

y2=-0.000 28x1+0.000 611 38x2-0.000 472x3-0.000 163 22x4+0.001 058x5-0.000 154x6-0.070 8

y3=0.002 85x1-0.001 554x2-0.001 347x3-0.000 476x4+0.000 179 36x5-0.000 155x6-0.070 7

y4=-0.000 943 38x1+0.001 915x2-0.001 347x3-0.000 476x4+0.000 179 35x5-0.000 155x6-0.043 7

if(y1>-0.013 2&y1<-0.014&y2>-0.010 9&y2<-0.012&y3>0.007&y3<0.009 7&y4>0.067&y4<-0.066)

上式中，x1,x2,x3,x4,x5,x6为灵敏度较高硬点坐标值，y1,y2,y3,y4为优化分析目标响应值，-10:1:10 为硬点坐标值xi变化范围。在MATLAB的编写搜索程序中，if判断语句的条件为根据需要对目标响应值范围进行约束[8]，可以计算出多组可满足设定范围内下硬点坐标值，更加有利于选择理想曲线。

3 前悬架多目标优化

3.1 确定设计变量及约束条件

为简化优化数学模型的过程和提高寻找最优解收敛性，采用加权的方法并根据上述分析各个参数之间的数学关系，即把主销后倾角和主销内倾角加权组合成一个综合目标函数、车轮前束角与车轮外倾角加权组合一个综合目标函数[9]，使前后两者之间匹配关系相当，简化整合优化目标函数如式(4)和式(5)所示。

f1=ω1y1+ω2y2

(4)

f2=ω3y3+ω4y4

(5)

式中：ωi为各优化函数的权重因子；y1、y2、y3、y4分别为主销后倾角、主销内倾角、车轮前束角、车轮外倾角；f1、f2为综合目标函数。一般情况下考虑到本次的优化仿真计算的简便性以及各分目标函数对操纵稳定性的影响程度大小，选用直接加权法计算权重因子，步骤如式(6)、式(7)、式(8)所示。

若已知某一分目标函数yi的变化范围为：

αi≤yi≤βi(i=1,2,3,4)

(6)

则称：

(7)

为该评价指标的容限Δyi，于是取该指标的权值为：

ωi=1/(Δyi)2(i=1,2,3,4)

(8)

计算出悬架各定位参数优化目标的权重因子结果统计见表1。

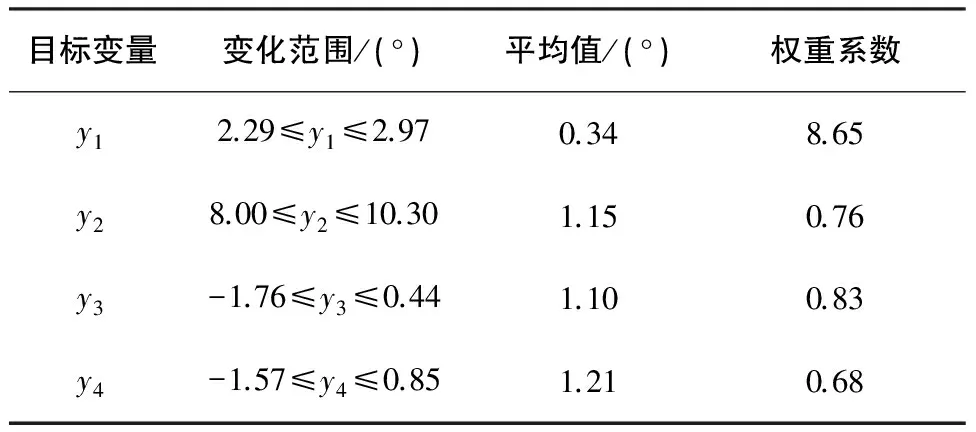
表1 各优化变量的权重因子

根据表1中各个分目标函数的权值系数，代入式(4)和式(5)中可得到加权组合处理后优化目标函数为：

f1=8.65y1+0.76y2

(9)

f2=0.83y3+0.68y4

(10)

经过加权组合整理后，将悬架特性结构参数优化问题转变成对两个目标函数的优化问题，即：f1为转向节定位目标函数；f2为主销定位目标函数。综合考虑操作稳定性能对硬点位置的影响大小和前悬架的硬点位置空间布置要求，得到的优化设计变量的优化空间见表2。

表2 各个优化设计变量的取值范围

3.2 确立目标函数与求解

利用已经建立好的近似数学模型以及所述的约束条件，把对悬架系统的优化设计多目标数学模型可表示为式(11)所示：

(11)

采用MATLAB其工具箱编写目标函数，采用改进型遗传算法最终得到了多目标优化问题的最优Pareto解集边界[10]，见图5所示。

图5 最优Pareto前端解集

由图5可知，A点和D点分别是f1和f2的极小值点，在AB段和CD段的很小的变化都会产生对f1，f2的影响，所以说这两个区间都不是最好的选择段，一般在前沿面相对平缓的BC段中选择最优点。为了同时满足f1和f2的解同时达到最优，取最优解集的中间值，通过比较各种设计结果，最后平衡各个目标，选用了一组较优响应设计变量值如式(12)所示，优化结果能使整车获得优异的操纵稳定性能。

X=(x1,x2,x3,x4,x5,x6)=(-579.51,-129.78,-91.46,-89.75,37.83,-31.27)

(12)

4 优化结果对比分析

将用两种方法求解的最优解重新带入到悬架模型中，再一次在虚拟样机中进行仿真试验分析，并与原始仿真结果进行对比分析，验证优化方法的可靠性。得出各目标在优化前后的结果曲线对比如图6-图9所示，优化前后目标变量变化范围统计见表3。

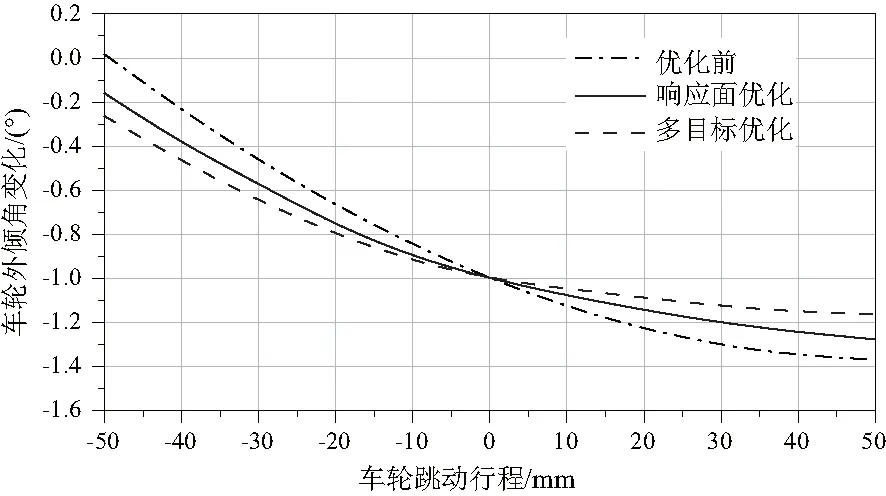
图6 车轮外倾角优化前后变化曲线

图7 主销后倾角优化前后变化曲线

图8 前轮前束角优化前后变化曲线

图9 主销内倾角优化前后变化曲线

表3 各车轮定位参数优化前后变化对照表 单位(°)

由仿真分析结果可知，车轮外倾角和前轮前束角的变化范围明显减小，虽然主销后倾角和主销内倾角减小范围不是很明显，但是与理想设计的要求相一致。结合图示对比分析来看，两种方法都使悬架车轮定位参数得到优化，但是多目标方法优化的结果比响应面方法优化的结果较好一些。这是由于在多目标优化的过程中综合考虑了弹簧刚度和轮胎径向刚度在汽车行驶过程中影响的原因，不仅有利于整体操纵稳定性的提高，也有利于减小轮胎偏磨，优化后的悬架性能更能反映真实运动的情况。

5 结语

为了进一步优化设计变量，改善整车操纵稳定性能，运用响应面和多目标优化方法分别对悬架模型中硬点参数进行优化，在优化过程中编写if判断语句函数模拟更换硬点的过程，提高优化工作效率。 比较响应面法与多目标方法优化前悬架特性参数前后优化结果，突出了多目标优化的优势，提高整车操纵稳定性。

[1] 董恩国，张蕾，申炎华. 基于2阶响应面模型的汽车前轮定位参数设计研究[J]. 汽车技术，2007(11)；22-25.

[2] 刘伟，史文库，桂龙明，等. 基于平顺性与操纵稳定性的悬架系统多目标优化.[J]. 吉林大学学报，2011(41)；1200-1204.

[3] 王世东. 基于响应面法的某轿车操纵稳定性仿真分析与优化[D]. 长沙：湖南大学，2011.

[4] 陈静，伍军，陈金华. 一种改进的非支配排序多目标遗传算法[J]. 计算机工程与应用，2009，45(29)：60-63.

[5] 赵妞. 基于ADAMS的双横臂悬架系统仿真[J]. 木工机床，2013(2)：21-23.

[6] 孙经来. 重型商用车操纵稳定性分析及参数匹配[D]. 长春：吉林大学，2010.

[7] 王伟. 基于虚拟样机技术的汽车操纵稳定性研究[D].武汉：武汉理工大学，2011.

[8] Liu Bo，Wang Ling，Jin Yihui. An effective hybrid particle swarm optimization for no-wait for low shop scheduling[J]. International Journal of Advance Manufacturing Techno logy，2007,31(9/10)：1001-1011.

[9] Dek K，Pratap A，Agarwal S，etal. A Fast Elitist Non-Dominated Sorting Genetic Algorithm for Multi-Objective Optimization: NSGA-Ⅱ.Kan GAL report 20001[J]. Indian Institute of Technology， 2000，6(2)：182-197.

[10] Abdullah Konak， David W. Coit，Alic E.Smith. Multi-objective optimization using genetic algorithms: A tutorial[J]. Reliability Engineering and System Safety， 2006，91(9)：922-1007.