分层式蓄热室蓄热过程数值仿真与优化

胡德胜，曾 祺



分层式蓄热室蓄热过程数值仿真与优化

胡德胜1，曾 祺2

（1中南大学资产经营有限公司，湖南 长沙 410083；2中南大学能源科学与工程学院，湖南 长沙 410083）

以降低熔铝炉蓄热室压损和提高蓄热室蓄热效率为目标，对某铝厂熔铝炉蓄热室进行了分层布料仿真研究。以多孔介质模型为基础，对动量方程源项进行了修正，将多孔介质结构内的传热转化为两相间的传热，并采用双能量方程形式建立多孔介质和流体间的传热能量方程。利用计算流体力学软件Fluent及其二次开发平台，建立了适用于蓄热室蓄热过程的数学模型。利用建立的数学模型对影响分层布料蓄热室蓄热过程的4个主要参数进行了模拟计算，得到了各参数对分层布料蓄热室的蓄热效率和压损的影响规律，并通过正交试验直观分析和方差分析的方法对各参数进行了显著性分析，且得到了保证蓄热效率和降低压损为目标的最优搭配方案。其中热效率最优搭配方案为入口质量流量1.65 kg/s、粒径组合26 mm -18 mm -26 mm、上中下层高比为2∶1∶2；压损最优搭配方案为入口质量流量1.65 kg/s、粒径组合32 mm -24 mm -32 mm、上中下层高比为2∶1∶2。

熔铝炉；蓄热室；多孔介质；数值模拟；正交试验

储能是解决能源供需不匹配的重要手段之一[1]，而蓄热式热交换器的蓄热室特性研究是目前工业热设备储能技术的重要研究方向。蓄热室的工作过程如图1所示，分为蓄热阶段和放热阶段，处于蓄热阶段时，高温烟气由蓄热室入口进入，流经蓄热介质并与其进行热交换，蓄热介质吸热升温，烟气放热降温后由烟道排出；处于放热阶段时，冷空气由风道流入蓄热室，在流经蓄热介质时吸热升温，蓄热介质温度降低。在实际使用中，蓄热室多成对布置，通过多个蓄热室交替吸放热，实现余热的回收利用。影响蓄热室蓄热效率与流动特性的因素众多，如气体流量、填充介质、填充球径、换向时间、孔隙率等[2-6]。设计和使用合理的蓄热室参数是改善和提高其流动特性和传热特性的关键所在。

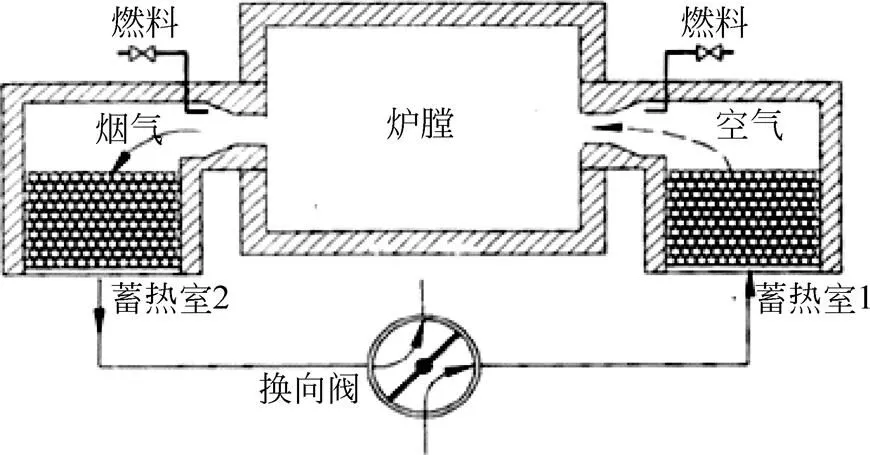
图1 蓄热流程示意图

现阶段，国内外学者通过实验和数值计算的方法对蓄热室流动和传热特性进行了研究。祁霞等[7]以实验研究的方法分析了气体流量、球径、孔隙率等参数对蓄热室阻力的影响，并依据结果修正了厄根公式系数；李萍等[8]利用填充球式蓄热室蓄热放热过程模拟系统分析了蓄热室几何参数、外界操作参数对热效率的影响；WANG等[9]利用数值仿真的方法对填充床蓄热室进行研究，得到影响蓄热室蓄热能力的主要参数为填充球粒径、填充床厚度和流速等；蔡九菊等[10]利用数值计算的方法研究了填充球式蓄热室结构参数和操作参数对传热特性的影响；胡思科等[11]采用氧化镁作为蓄热体，以空气作为能量传播介质，研究了不同孔隙对蓄热室内不同位置传热和流动特性的影响；AJDARI等[12]对填充球蓄热室进行了数值计算，研究了气体速度、加热和放热转换周期、球径等参数对蓄热室影响，讨论了系统效率随各因素的变化规律。目前所做研究均采用单粒径球形或蜂窝形蓄热体形式，具有高效、结构紧凑等特点，但对于烟气量大的熔铝炉，单一布置形式不能最大限度地吸收热量，烟气通过蓄热室后仍有大量热量被浪费且设备的成本较高。为在提升余热利用率的同时降低成本，本工作提出了一种按粒径分层布置的分层式蓄热室结构，并对影响分层式蓄热室蓄热效率和流动损失的各因素进行优化分析，获得了分层式蓄热室的最优结构参数。本工作的研究对填充球式蓄热室的设计、运行及工业应用都有重要意义。

1 模型的建立与验证

1.1 物理模型

蓄热室由上部分的梯台和下部分的方形箱组成，气体经顶部梯台口流入，经设置在方箱底部的长方形篦孔流出，其尺寸为实测值。蓄热室模型如图2所示。

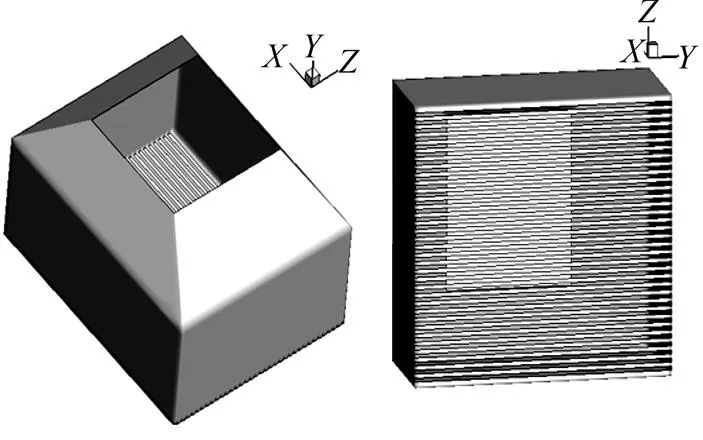
图2 蓄热室几何模型图

由于蓄热室中填充球数量巨大，填充球之间的间隙形状不规则，气体在填充球间间隙的流动和传热过程较为复杂，难以准确的进行计算，且对后续的网格离散处理造成难题，因此有必要对蓄热室进行平均化和统计处理。经处理后，填充球相当于多孔介质，气体穿过填充球间间隙的过程相当于流经多孔介质的过程，故将蓄热室内部填充球简化为多孔介质模型。

1.2 数学模型

本工作对蓄热室的研究围绕蓄热过程展开，其主要的物理现象包括传热和流动。传统的多孔介质模型采用单一能量守恒方程，认为流体和多孔介质之间的换热过程十分迅速，两者的温度保持相同。但实际过程中，多孔介质和流体之间存在明显的温差，单一能量方程并不能满足流体和多孔介质间存在换热的情形，因此采用双能量方程形式，即将流体和蓄热介质作为两种不同的连续介质，在任意点和对应体积单元，分别定义固态相平均温度和液态相平均温度，从而将多孔介质结构内的传热化为两种物相之间的传热，通过用户自定义函数（user defined function，UDF）编写了计算方程中关于导热项、源项和单位体积的对流传热系数等的相关定义和计算，固相和液相能量方程[13-14]分别为：

固相：

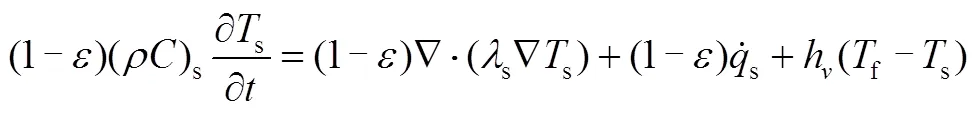
气相：

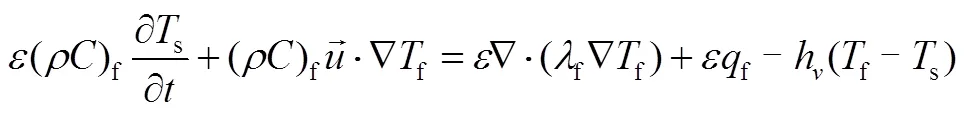
利用Achenbach准则[15]关系式计算h：

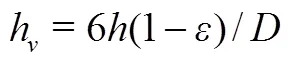
其中由式(4)确定：

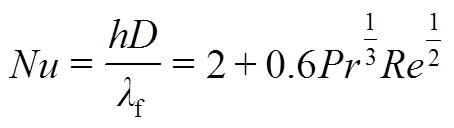
为模仿多孔介质作用，需要在动量方程中加入一个源项。该源项由惯性损失、黏性损失组成。对于简单均匀介质可使用式(5)计算

本工作采用Ergun方程计算黏性阻力系数（1/）和惯性阻力系数（2）：

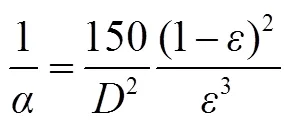
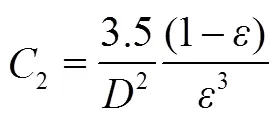
仿真模拟的边界条件为现场实测数据，测试项目包括蓄热球材质、蓄热球直径、环境温度、蓄热室入口烟气温度、烟气流量，测试方法和所用仪器如表1所示。

表1 边界条件测试表

热电偶的测点和微电脑平行采尘仪的开孔位置如图2所示。每个测试点均测量3次，取其平均值作为最终测试值。

基于上述物理、数学模型和边界条件进行仿真计算，仿真计算结果通过出口烟气温度进行验证。出口烟气温度的测量由0.3 mm线热电偶（K型）和数据分析设备（Fluke，Hydra Data Logger 2625A， Germany）完成，热电偶安装于蓄热室出口下端烟道处，测试点的位置如图2所示。由仿真计算 得到的出口烟气温度与现场测试得到的数据如表2所示。

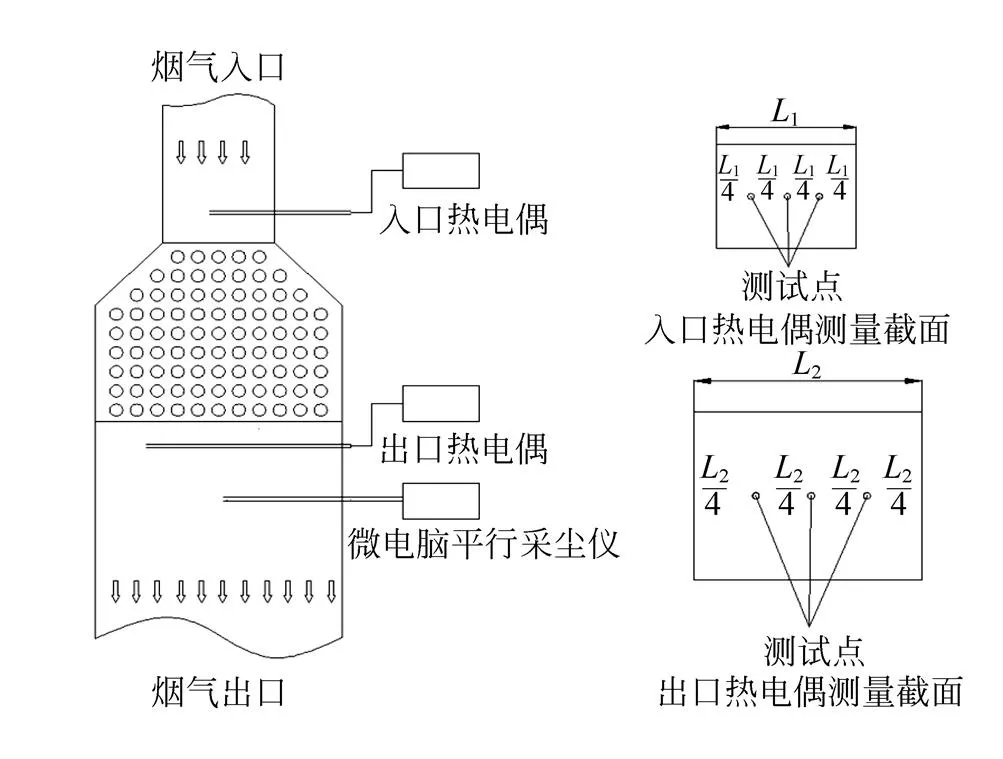
图3 测点位置图

表2 烟气出口温度验证表

从表2可以看出，现场测试数据与模拟数据误差均在8%以内，证明该仿真模型具有可靠性，其它的因素分析可基于该模型进行。

2 分层式蓄热室结构的提出

蓄热效率和压损分别是蓄热室主要的传热性能评价指标和流动性能评价指标，其计算式如式(8)、式(9)所示。

蓄热效率：

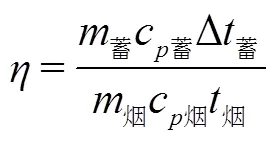
压损：

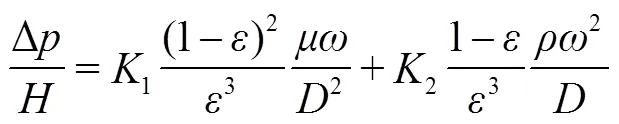
以上述计算模型和边界条件对铝厂熔铝炉蓄热室进行仿真计算，得到其热效率和压损分别为81.9%、2321 Pa/m，蓄热室的压损并不太大。为了在保证压损增加较小的情况下，较大的提高热效率，提出一种在蓄热室中间填充较小直径填充球的分层式布置形式，形成上层和下层粒径大、中层粒径小的分层结构形式。

取上、中、下层高之比为1∶1∶1，取上、下层填充球直径为30 mm，中层填充球直径为22 mm，以上述计算模型和边界条件进行仿真计算。蓄热结束时，填充球直径30 mm -22 mm -30 mm的分层式蓄热室与填充球直径30 mm的单层蓄热室的温度分布云图如图4所示。

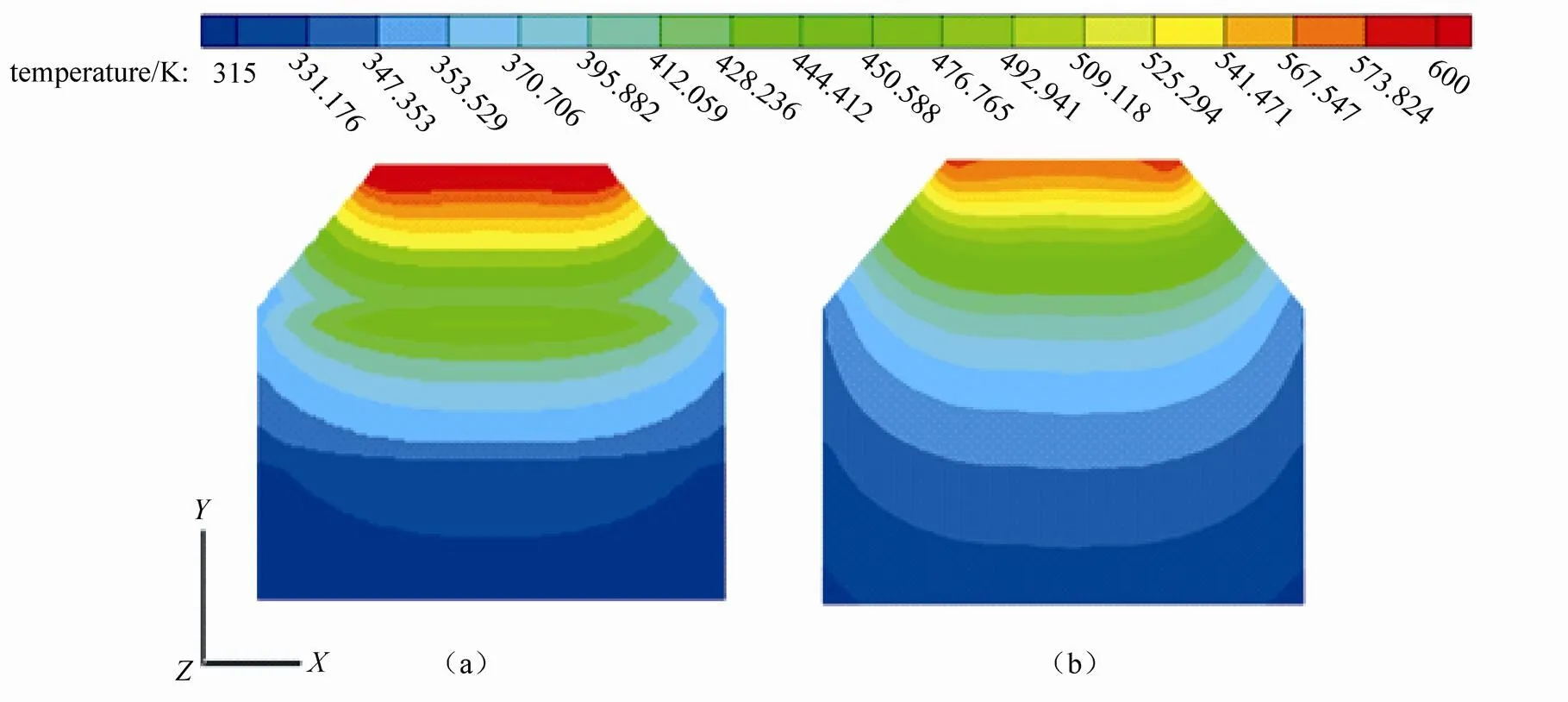
图4 分层式蓄热室（a）与单层蓄热室（b）温度云图

单层蓄热室温度沿烟气流动方向逐渐降低。分层式蓄热室在上层区域温度分布与单层蓄热室一致。当流至上、中层交界面时，由于粒径减小，比表面积增大，对流换热增强，因此在交界面处产生较高温区，随后蓄热室温度沿烟气流动方向逐渐降低且降低速率比单层时快；当流至中、下层交界面时，由于粒径增大，比表面积减小，对流换热减弱，故蓄热室温度下降速率降低。

单层蓄热室和分层式蓄热室蓄热效率和压损如表3所示。

表3 单层、分层式蓄热室蓄热效率和压损

在单粒径30 mm布置形式下，采用分层式布置结构进行改造，可以有效地提高热效率和热均匀性，压损相对30 mm布置形式增加不大且远小于采用单粒径22 mm布置形式。故采用分层式布置结构对单粒径30 mm蓄热室进行改造是合理有 效的。

3 单一参数对分层式蓄热室蓄热过程影响的仿真

利用已经建立的计算模型，针对影响分层式蓄热室蓄热的4个主要参数：入口质量流量、上（下）层粒径、中层粒径、上中下层高比，在除研究对象外其它参数[入口质量流量1.925 kg/s、上（下）层粒径mm、中层粒径mm、上中下层高比1∶1∶1]不变的情况下，研究单一参数对分层式蓄热室蓄热过程的影响规律。上述4个参数取值如表4所示。通过对20组工况进行计算，得到入口质量流量、上（下）层粒径、中层粒径、上中下层高比对分层式蓄热室蓄热过程的影响，并对计算结果作出如下分析。

3.1 入口质量流量对分层式蓄热室蓄热过程的影响

不同入口质量流量条件下，蓄热室的热效率及压损变化曲线如图5所示，蓄热室的蓄热量变化曲线如图6所示。

表4 数值模拟计算参数取值表

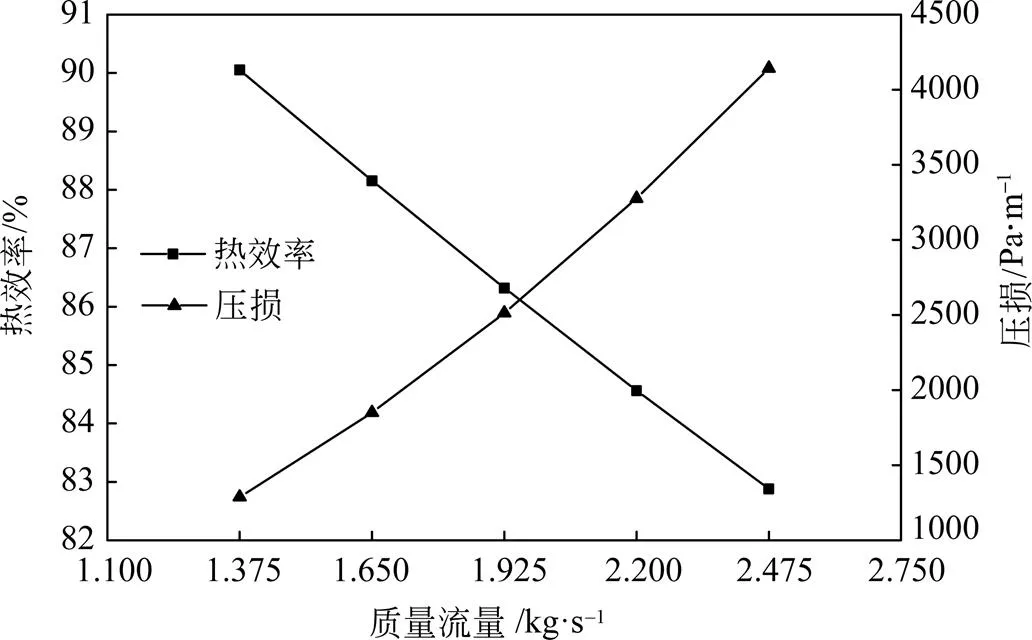
图5 入口质量流量对分层式蓄热室的热效率及压损的影响

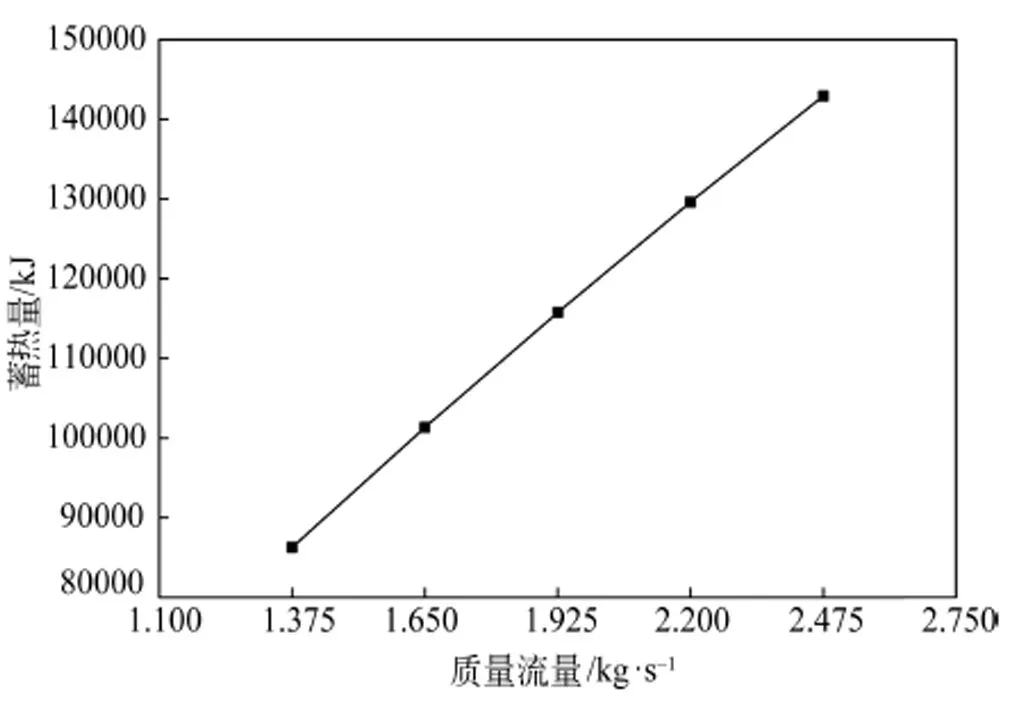
图6 入口质量流量对分层式蓄热室的蓄热量的影响

由图5、图6可知，在入口质量流量为1.375 kg/s、1.65 kg/s、1.925 kg/s、2.2 kg/s、2.475 kg/s时，蓄热效率分别为90.1%、88.2%、86.3%、84.6%、82.9%，蓄热室蓄热量分别为86277.9 kJ、101354 kJ、115785.1 kJ、129628.9 kJ、142932.7 kJ。说明随着入口质量流量的增加，蓄热室的蓄热效率降低，这是由于入口质量流量增加，加强了流体和蓄热球之间的对流传热，使单位时间内的换热量增加。但蓄热室的导热能力存在上限，流量过大时，烟气中多余的热量不能被蓄热球完全吸收而排出体系，造成蓄热效果不升反降，故在蓄热室设计过程中，要考虑到蓄热球余热能力和质量流量之间的匹配。

由图5可知，在入口质量流量为1.375 kg/s、1.65 kg/s、1.925 kg/s、2.2 kg/s、2.475 kg/s时，压损分别为1288.5 Pa/m、1850.0 Pa/m、2513.1 Pa/m、3276.8 Pa/m、4142.0 Pa/m。说明随着入口质量流量的增加，流经蓄热室的压损增大，由Ergun公式得，压力损失与质量流量变化成正比例关系，仿真情况与其 一致。

3.2 粒径对分层式蓄热室蓄热过程的影响

不同粒径条件下，蓄热室的热效率及压损变化曲线如表5所示。

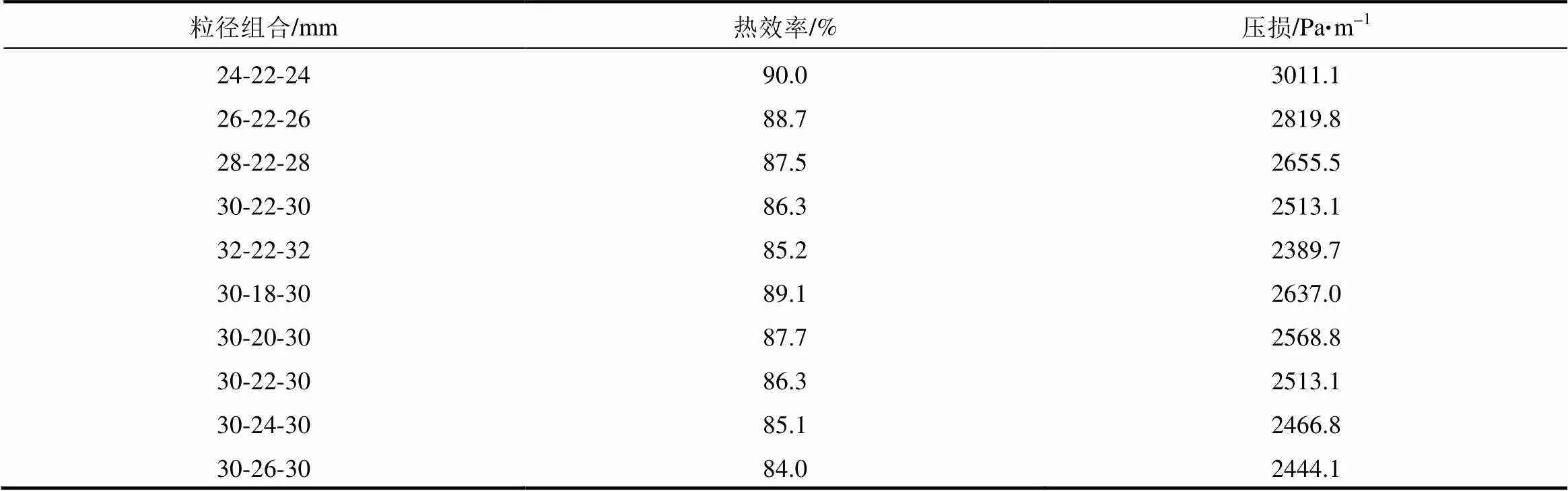
表5 粒径对分层式蓄热室的热效率及压损的影响

注：粒径组合含义为上层粒径-中层粒径-下层粒径。

由表5可知，蓄热效率随粒径的增大而逐渐降低，这是由于随着粒径的增大，氧化铝球的比表面积相应减小，导致对流换热效果变差，因此蓄热效率随粒径的增大而逐渐降低。由表5可知，压损随粒径的增大而逐渐降低，这是由于随粒径的增大，烟气流经填充球区域时，相应的黏性阻力和惯性阻力减小，压损相应减少，故压损呈现随粒径增大而逐渐下降的趋势。

3.3 上中下层高比对分层式蓄热室蓄热过程的影响

不同上中下层高比条件下，蓄热室的热效率及压损变化曲线如图7所示。

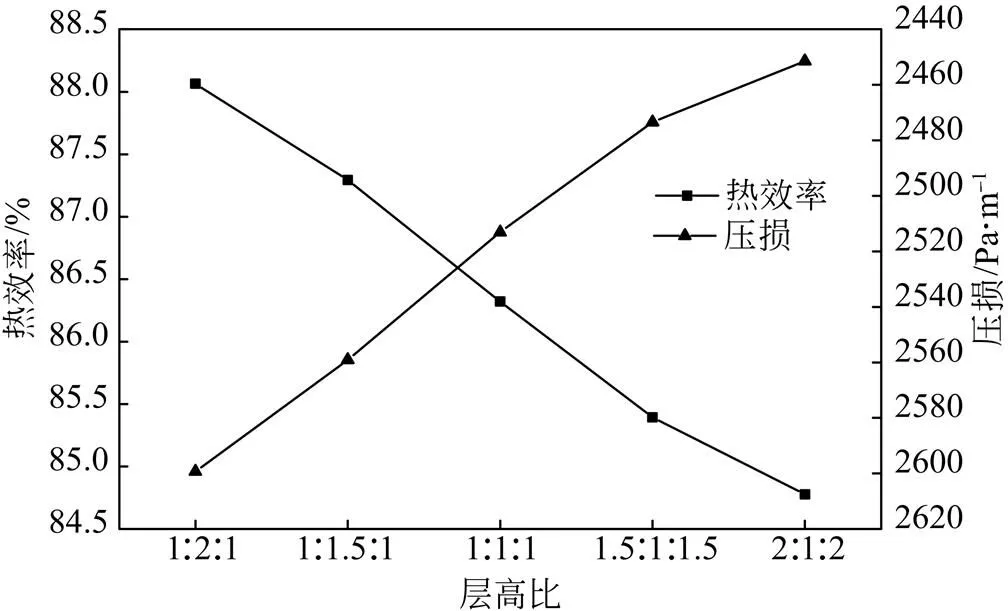
图7 上中下层高比对分层式蓄热室的热效率及压损的影响

由图7可知，在上中下层高比为1∶2∶1、1∶1.5∶1、1∶1∶1、1.5∶1∶1.5、2∶1∶2时，蓄热效率分别为88.1%、87.3%、86.3%、85.5%、84.8%，压损分别为2599.3 Pa/m、2559.1 Pa/m、2513.1 Pa/m、2463.7 Pa/m、2451.4 Pa/m。说明蓄热效率和压损均随着上中下层高比的增大而减小，这是由于随着上中下层高比的增加，小粒径蓄热球减少，比表面积减少，导致对流换热效果变弱。

4 正交优化

利用正交试验对入口质量流量、上（下）层粒径、中层粒径、上中下层高比4个参数的4种水平进行优化分析。选择正交表L16（45）进行试验，优化评价指标为蓄热效率和压损，试验结果如表6所示。

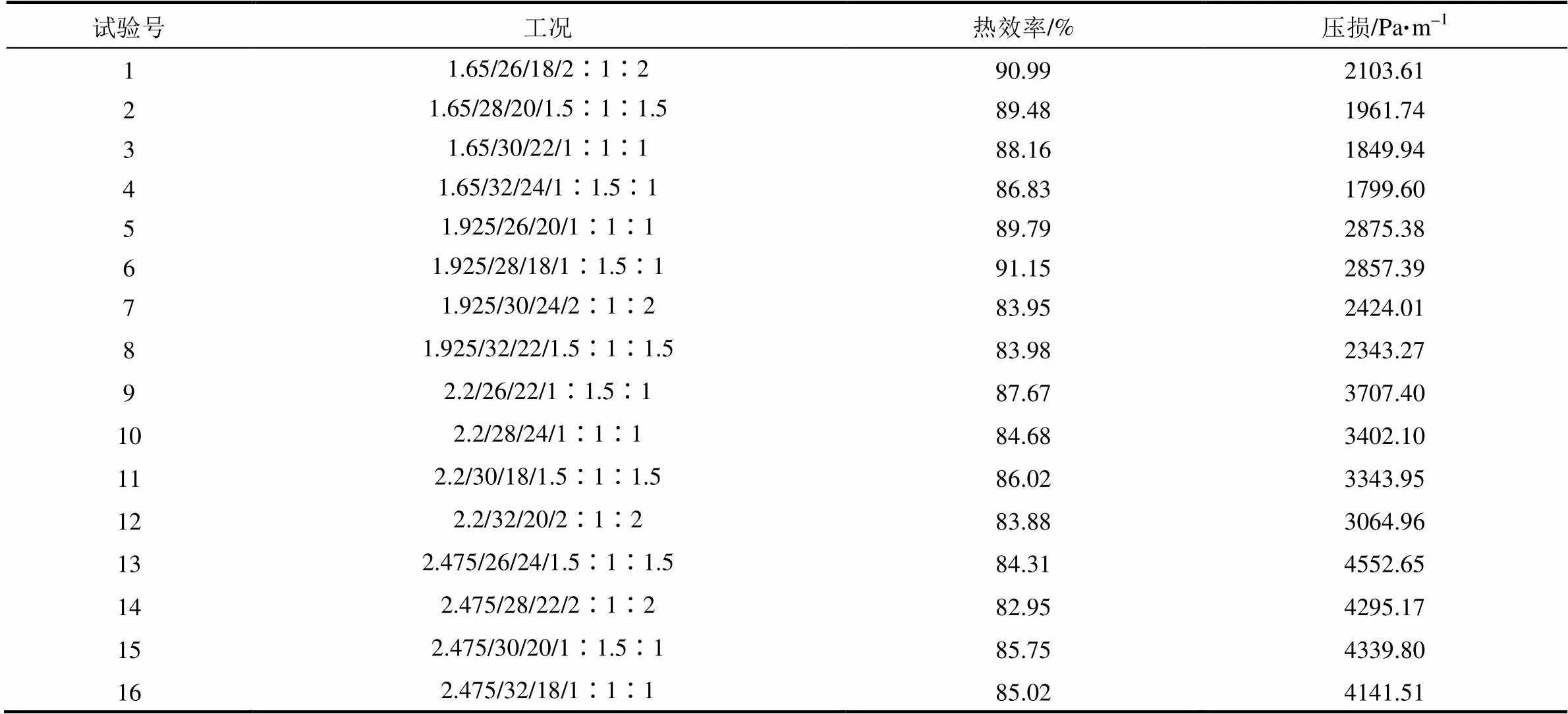
表6 正交实验结果

注：表中工况形式为质量流量（kg/s）/上（下）层粒径（mm）/中层粒径（mm）/上中下层高比。

对正交试验结果进行直观分析，得到直观分析表如表7所示。

由表7可知，影响分层式蓄热室热效率的各因素重要顺序为入口质量流量>中层粒径>上（下）层粒径>上中下层高比，影响分层式蓄热室压损的各因素重要顺序为入口质量流量>上（下）层粒径>上中下层高比>中层粒径。蓄热室的热效率越高越好，压降越小越好，因此由各因素水平对应的k值得到最优设计组合为：热效率最优搭配方案为入口质量流量1.65 kg/s、粒径组合26 mm-18 mm-26 mm、上中下层高比2∶1∶2；压损最优搭配方案为入口质量流量1.65 kg/s、粒径组合32 mm-24 mm-32 mm、上中下层高比2∶1∶2。

对正交试验结果进行方差分析，如表8所示。

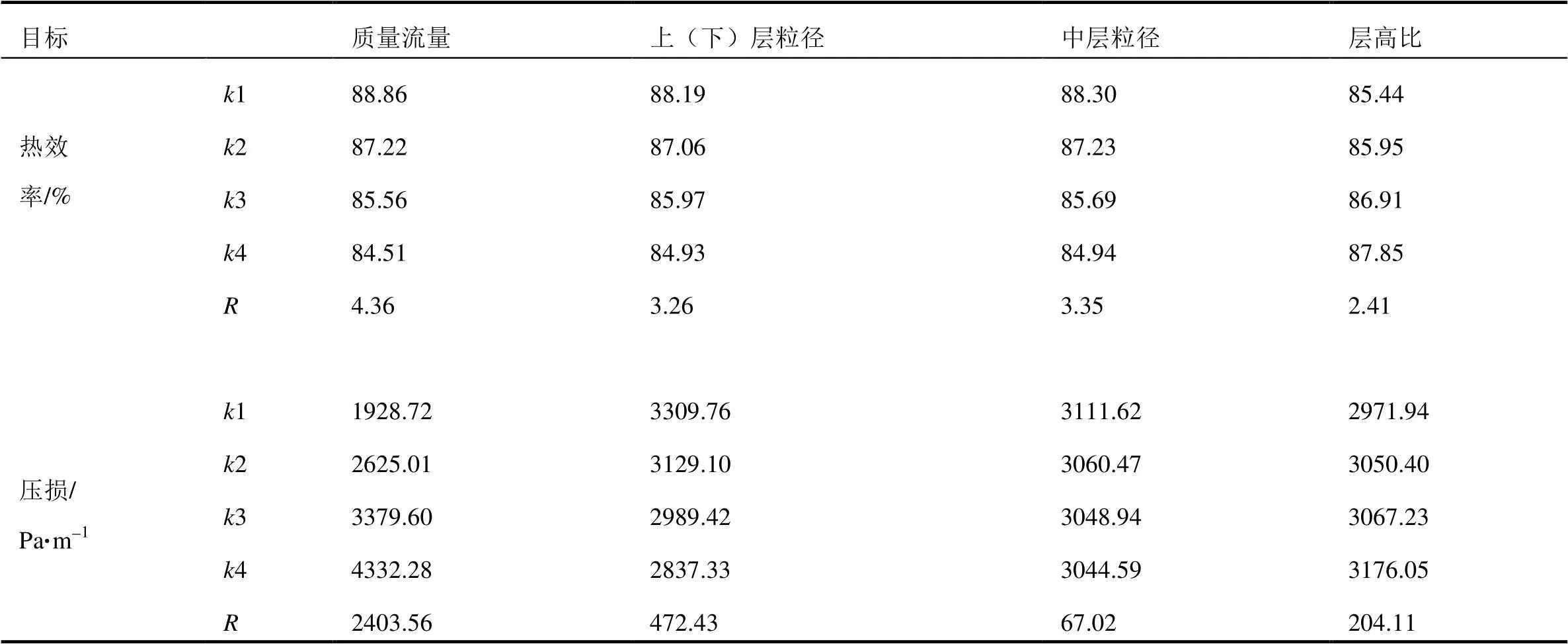
表7 正交结果直观分析

注：表中表示正交表中任一列上因素取水平时所得试验结果的算术平均值，表中R表示极差。

表8 正交结果方差分析

续表

目标质量流量上（下）层粒径中层粒径层高比随机误差总和 压损/ Pa·m-1平方和127587374862111144084810318313344381 自由度3333315 均方425291216207023813282701061 F值4008.32152.753.5926.64—— F0.01—29.46———— 显著性**————

由表8可知，入口质量流量、上（下）层粒径、中层粒径在0.01水平上对分层式蓄热室热效率影响显著，入口质量流量、上（下）层粒径在0.01水平上对分层式蓄热室压损影响显著，因此，要增大蓄热室的蓄热效率和降低蓄热室压损。最主要的是在条件允许范围内尽量降低入口质量流量或改变上（下）层粒径大小；其次可以综合考虑实际情况调整中层粒径大小。

5 结 论

本工作建立了蓄热室的物理、数学和仿真模型，并通过实测数据验证了模型的准确性。随后提出了一种分层式布置形式的蓄热室结构，来保证热效率的同时避免压损过大，并从数值计算的角度对影响分层式蓄热室热效率和压损的各参数进行研究。

基于非热力学平衡的双能量方程和平均化以及统计处理的多孔介质模型所建立的蓄热室蓄热过程模型模拟得到的60 s内烟气出口的平均温度和实测值之间的误差在5%以内，验证了该模型的准确性。

提出了分层式布置形式的蓄热室结构，并利用上述模型计算了入口质量流量、上（下）层粒径、中层粒径、上中下层高比对分层式蓄热室蓄热过程的影响，并以蓄热效率和压损为优化目标对分层式蓄热室4个结构参数进行了正交优化，得到了最优工况为：以保证热效率为主时的最优搭配方案为入口质量流量1.65 kg/s、粒径组合26 mm-18 mm-26 mm、上中下层高比2∶1∶2；以降低压损为主时的最优最优搭配方案为入口质量流量1.65 kg/s、粒径组合32 mm-24 mm-32 mm、上中下层高比2∶1∶2。

符 号 说 明

C2——惯性阻力系数，1 Cs，Cf——分别为固相和气相比热容，J·(kg·K)-1 Cp蓄，Cp烟——分别为蓄热球和烟气在相应温度时的平均比热容，J·(kg·K)-1 D——蓄热小球直径，m hv—— 气、固相间单位体积对流传热系数，J·(m3·s·K)-1 H——蓄热室的填充层高度，m K1，K2——Ergun试验系数，1 m蓄，m烟——分别为蓄热球总质量、流入烟气总质量，kg Nu——Nusselt数，1 Pr——Prandtl数，1 Dp——蓄热室的总压降，Pa qs，qf——分别为气、固相反应热，W·m-3 Re——Reynolds数，1 Si——源项，kg·m-3 t——时间，s Dt蓄——蓄热室的平均温度变化，K t烟——烟气的入口温度，K Ts，Tf——分别为气、固相温度，K u——速度，m·s-1 umag——绝对速度，m·s-1 w—— 蓄热室球层单位时间单位截面烟气流量，m·s-1 1/a——黏性阻力系数，1 r——密度，kg·m-3 e——孔隙率，1 λ——热导率，W·(m·K)-1 h——热效率，1 m——动力黏度，Pa·s

[1] 王艳, 白凤武, 杨贝, 王志峰. 高温显热-潜热复合储能系统传热特性研究[J]. 储能科学与技术, 2017, 6(4): 719-725.

WANG Yan, BAI Fengwu, YANG Bei, WANG Zhifeng. Study on heat transfer characteristics of high temperature sensible heat and latent heat composite energy storage system[J]. Energy Storage Science and Technology, 2017, 6(4): 719-725.

[2] 唐福恒. 玻璃熔窑蓄热室筒形、条形、十字形格子砖的应用对比[J]. 玻璃, 2018, 45(1): 16-29.

TANG Fuheng. Application comparison of cylindrical, strip and cross lattice bricks in regenerator of glass furnace[J]. Glass, 2018, 45(1): 16-29.

[3] 吕志超, 周丽雯, 刘坤, 等. 蜂窝陶瓷蓄热体传热及气体流动特性的数值模拟[J]. 冶金能源, 2017, 36(S2): 43-45.

LV Zhichao, ZHOU Liwen, LIU Kun, et al. Numerical simulation of heat transfer and gas flow characteristics of honeycomb ceramic regenerator[J]. Energy for Metallurgical Industry, 2017, 36(S2): 43-45.

[4] 温良英, 韩明荣, 董凌燕, 等. 高效蓄热室阻力及传热特性[J]. 燃烧科学与技术, 2005, 11(6): 506-510.

WEN Liangying, HAN Mingrong, DONG Lingyan, et al.Resistance and heat transfer characteristics of high efficiency regenerator[J]. Journal of Combustion Science and Technology, 2005, 11(6): 506-510.

[5] 刘颖, 刘义平, 陶曙明, 等. 填充球蓄热室内传热与流动过程数值模拟及结构优化[J]. 中南大学学报(自然科学版), 2015, 47(6): 1981-1988.

LIU Ying, LIU Yiping, TAO Shuming, et al.Numerical simulation and structural optimization of heat transfer and flow in packed sphere regenerator[J].Journal of Central South University(Science and Technology), 2015, 47(6): 1981-1988.

[6] 刘映辉, 张治. 散堆拉西环蓄热室热工特性的数值模拟[J]. 热能动力工程, 2011, 26(5): 555-560.

LIU Yinghui, ZHANG Zhi.Numerical simulation of thermal characteristics of rash regenerator in bulk reactor[J]. Journal of Engineering for Thermal Energy and Power, 2011, 26(5): 555-560.

[7] 祁霞, 戴方钦. 蓄热小球填充床的气体阻力特性[J]. 过程工程学报, 2015, 15(5): 770-773.

QI Xia, DAI Fangqin. Gas resistance characteristics of regenerative ball filled bed[J]. The Chinese Journal of Process Engineering, 2015, 15(5): 770-773.

[8] 李萍, 曾令可. 填充球蓄热室热效率影响因素数值分析[J]. 工业加热, 2008, 37(5): 19-22.

LI Ping, ZENG Lingke. Numerical analysis of factors affecting thermal efficiency of packed ball regenerator[J]. Industrial Heating, 2008, 37(5): 19-22.

[9] WANG S B, HUA W. A numerical simulation about thermal processing of the regenerator in the regenerative chamber[J]. Challenges of Power Engineering and Environment, 2007(1): 1342-1346.

[10] 蔡九菊, 饶荣水. 陶瓷球蓄热室传热特性的研究[J]. 钢铁, 1999(2): 39-44.

CAI Jiuju, RAO Rongshui. Study on the heat transfer characteristics of the ceramic ball regenerator[J]. Iron&steel, 1999(2): 39-44.

[11] 胡思科, 邢姣娇. 固体蓄热装置的蓄、放热特性数值模拟分析[J]. 流体机械, 2014, 42(8): 78-83.

HU Sike, XING Jiaojiao. Numerical simulation analysis of storage and exothermic characteristics of solid heat storage device[J]. Fluid Machinery, 2014, 42(8): 78-83.

[12] AJDARI H R B, SADRAMELI S M. Theoretical and experimental studies of a thermal regenerator for heat recovery in aluminum melting furnaces[M]. New York: Springer International Publishing, 2015: 437-443.

[13] LI J, TU S. Heat transfer of laminar flow over a plate embedded in porous medium with a constant heat flux under local non-equilibrium condition[J]. Journal of the Chemical Industry & Engineering Society of China, 2010, 61(1): 10-14.

[14] 刘伟, 范爱武, 黄晓明. 多孔介质传热传质理论与应用[M]. 北京: 科学出版社, 2006: 28-58.

LIU Wei, FAN Aiwu, HUANG Xiaoming. Theory and application of heat and mass transfer in porous media[M]. Beijing: Science Publishing Company, 2006: 105-210.

[15] HWANG K S, JUN J H, LEE W K. Fixed-bed adsorption for bulk component system. Non-equilibrium, non-isothermal and non-adiabatic model[J]. Chemical Engineering Science, 1995, 50(5): 813-825.

Numerical simulation and optimization of a heat storage process in a layered regenerator

HU Desheng1, ZENG Qi2

(1Central South University Asset Management Co., Ltd., Changsha 410083, Hunan, China;2College of Energy Science and Engineering, Central South University, Changsha 410083, Hunan, China)

This numerical study aims to reduce pressure loss and improve thermal efficiency of a regenerator of an aluminum smelting furnace. A porous medium based model with a modified source item of the momentum equation, coupled with energy equations for both gas and solid phases, which upon using suitable, was established for modelling the regenerative process in Fluent environment. The mathematical model was used to investigate the effects of 4 main parameters on the thermal storage process, storage efficiency and pressure loss of the stratified regenerator. The results were analyzed by using the orthogonal experiments and variance analysis, and the collocation scheme for an optimal regenerative efficiency and pressure loss minimization. It was found that an optimal regenerative efficiency occurs with an entrance mass flow of 1.65 kg·s-1, a particle size combination of 26 mm-18 mm- 26 mm, whereas the optimal pressure drop takes place with an entrance mass flow of 1.65 kg·s-1, a particle size combination of 32 mm-24 mm-32 mm, and the upper middle and lower layer high ratio at 2∶1∶2.

aluminum smelting furnace; regenerator; porous medium; simulation; orthogonal test

10.12028/j.issn.2095-4239.2018.0058

TK 02

A

2095-4239（2018）04-0718-08

2018-04-11；

2018-06-10。

胡德胜（1971—），男，硕士，研究方向为热工设备仿真E-mail：hdsf38@163.com；

曾祺，男，硕士研究生，研究方向为热能工程，E-mail：1542790825@qq.com。