非随机过程的地震激励下埋地压力管道的非概率可靠性分析*

张 鹏，王艺环，秦国晋

(1.西南石油大学 土木工程与建筑学院，四川 成都 610500；2. 西南石油大学 机电工程学院，四川 成都 610500)

0 引言

21世纪是地震频发的年代，长输埋地管道作为重要的生命线工程，在地震发生时的破坏，会带来严重的经济损失，甚至引发一系列次生灾害。管道作为1种结构形式，在进行抗震分析时，首要考虑的就是适当的地震动模型以及输入方式。相关研究表明，不同地震动模型会使得结构的反应变化呈现明显差异。随机振动是1门用概率与统计方法来研究受随机载荷结构系统的稳定性、响应、识别及可靠性的技术学科[1]，经典的随机振动理论是1种基于数学分析的体系，但在工程分析中无论是线性或非线性的结构都难以得出解析解，且计算工作量巨大[2]。在很多实际工程问题中获得样本需要巨额成本或者根本不可能获得足够样本信息。因此，以概率模型为基础的概率可靠性分析，通常需引入一些专家概率分布的假设;但对于传统的随机振动而言，概率分布相对于真实值只有微小的偏差都可能导致很大的分析误差[3]。针对地震信息记录客观因素限制所导致的地震实际激励信息样本十分有限，刘宁宇[4]建立了基于非概率凸模型过程理论描述传统随机过程的非随机振动分析方法，解决了样本信息缺乏的不确定振动分析。

传统的可靠性分析是基于大数据支持下的概率分析，但实际工程中基于专家经验的函数分布建立，带有较强的主观性；设计阶段的可靠度分析，结构参数也只能假定其分布规律；而复杂的结构分析不能以1个数学分布函数来描述。为了解决工程上的小样本、贫信息以及设计阶段参数问题，上世纪90年代初，Ben-Haim和Elishakoff将非概率凸模型理论引入到不确定分析中，并首次提出了非概率可靠性方法[5-7]；欧进萍等[8-10]则提出了模糊随机振动理论并用于地震荷载作用下具有模糊信息结构的随机动力可靠性分析。与模糊数学对不确定样本信息模糊化思想相似，非概率的集合理论凸方法仅需知道任意时刻的样本边界信息而非精确概率分布函数，因此在处理非精确概率分布的随机变量问题时表现出一定优越性，而一维的凸模型为区间模型。Zhan等[11]基于多椭球凸模型描述了不确定但有界的变量，提出了1种用于安全边缘量化的非概率可靠性指标的数学定义;Guo等[12]对比了参数不确定但有界结构振动控制的非概率可靠性方法和基于可靠性的设计;在对压力管道进行可靠性分析时，邵世飞等[13]为了弥补管道数据的不确定信息，运用非概率可靠性方法评价了压力管道的非概率指标。

综上，凸模型理论为仅有小样本数据的实际工程中关于随机振动分析以及可靠性设计提供了新的研究思路，并成为随机过程和概率可靠性理论的补充。

1 非随机过程

1.1 非随机过程定义

传统的随机过程是指定义于1个参数集的每一点处都有相对应的随机变量，其数值的大小是随着时间不断变化的。事物变化的全过程进行1次观测得到的结果是1个时间t的函数[14]。非概率凸模型过程描述不确定性激励，而非随机过程利用凸模型过程描述。

凸模型过程定义为：

任意时刻ti∈T，i=1，2，…，n。

X(ti)=[XL，XR]，且(X(t1)，X(t2)，…X(ti))的联合分布区域为1个凸集。

不确定过程X(t)的所有可能的类型和形状都将包含在上边界和下边界组成的区域内。如图1所示。

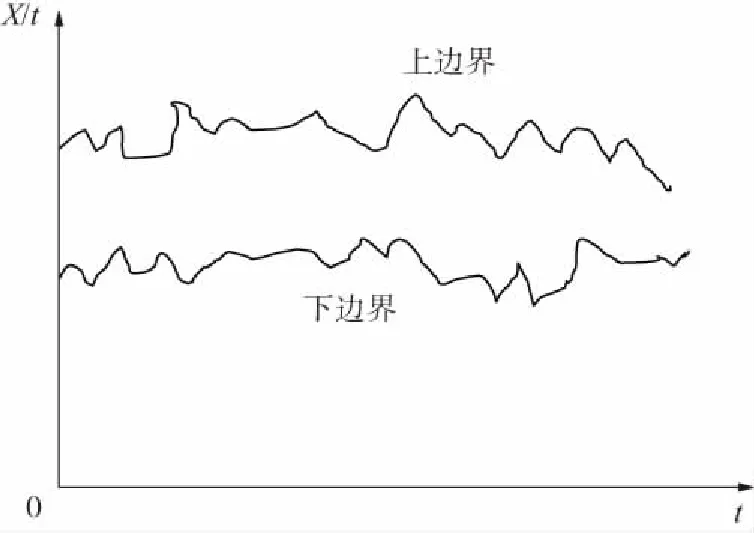
图1 凸模型过程Fig.1 Convex model process

一维凸模型为区间模型。当X(t)为一维区间数时，XL(t),XU(t) ∈R，则X(t)=[XL(t)，XU(t)]，则X为区间数[15]。

模型的几何特征可由中点和半径描述：

式中：XC(t)为中值函数，表示时间的变化趋势；XR(t)为半径函数，表示变化的幅度；ηx为变异系数函数，表示不确定水平[5]。

非随机过程可分为：中值恒定、半径恒定、变异系数恒定。分别如图2、图3和图4所示。

图2 中值恒定的非随机过程Fig.2 Median constant’s non-random process

图3 半径恒定的非随机过程Fig.3 Constant radius’s non-random process

图4 变异系数恒定的非随机过程Fig.4 Non-random process with constant coefficient of variation

1.2 地震荷载的非平稳非随机过程模型

实际地震动的非平稳性表现为强度和频率的非平稳性[16]。大多数工程仅将地震荷载作为平稳随机过程与一个强度包络函数的乘积来反应地震荷载强度的非平稳性。

A(t)=g(t)X(t)

(1)

式中：g(t) 为强度包络函数；X(t)为利用区间理论处理后的平稳随机过程。

在工程抗震中常选用下面的强度包络函数g(t)为[17]：

(2)

式中：c为衰减系数；选值参见文献[18]；t1为主震平稳段开始时刻;t2为主震平稳段结束时刻。t1，t2选值如表1所示。

表1 主震时间Table 1 Main time of earthquake

平稳非随机区间过程X(t)的模型为[4]：

(3)

式中：XR(t)为半径函数；K1为常数；XC(t)为中值函数；K2为常数；rXX(t1,t2)为自相关函数，与时间差|t2-t1|相关，与t1与t2的值无关。

2 埋地管道的动力分析

2.1 埋地管道的应力分析

大量研究表明[19-20]，埋地管道在遭受地震荷载的时候，轴向受力影响远远大于横向影响，故本文仅考虑管道在轴向抗震问题。根据非随机振动分析方法[21]，当随机过程被处理为区间过程，则结构的响应也应该为有上、下界的区间形式。

国内外研究表明[22-23]，地震荷载作用下埋地管道的轴向变形大大超过弯曲变形，故本文仅讨论管道轴向动力响应。

2.1.1 基本假定

作以下假设：

1)假定沿管道的场地条件以及土体参数均不变。

2) 与地基土阻尼相比管道阻尼极小，可忽略其本身的材料阻尼。

3)管道周围的土体简化为连续均匀分布的阻尼器和弹簧，如图5所示。

图5 埋地管道简化示意Fig.5 Buried pipeline’s simplified diagram

2.1.2 动力方程的建立及求解

建立管道在地震作用下的轴向动力方程为：

(4)

式中：m为管道的质量；u(t)为管道的轴向位移；c为管道周围介质的阻尼系数；k为管道周围的刚度系数；K为管道的轴向刚度；ug(t)为场地在地震作用下的轴向位移。

根据屈铁军等[24]研究结果，管道的轴向位移为场地位移引起的静态位移uS(t)和管道的惯性与阻尼引起的动态位移uD(t)2部分组成。令：

(5)

式中：x为所求地点的位置坐标；l为所选取管道长度；qi(t)为广义坐标。

根据振型分解法求得[24]：

(6)

(7)

(8)

有关研究表明[25]，内力分析时，动态位移远小于拟静态位移。因此本文忽略管道的动态反应。根据式(5)-(8)，可以得出管道在地震作用下的轴向位移通式为：

(9)

(10)

再根据σ=εE可得管道的应力σ：

(11)

2.2 埋地压力管道的动力响应分析

当埋地管道仅受内压作用时，用圆柱壳弹性理论求解管道的应力状态[26]，则：

(12)

式中：t为管道任意位置当前壁厚；D为管道直径；E为弹性模量；ν为泊松比；P为内压；w为管壁上任意点的径向位移，是轴向坐标x的函数。

在x=0时，周向应力σφ最大，由上式可得：

(13)

埋地长输管线受土壤的阻力而不能自由伸长，造成泊松应力，如图6所示。

图6 压力管道受力Fig.6 Pressure pipeline’s stress diagram

轴向应力σx可描述为：

(14)

式中：ν为泊松比，本文取0.3。

2.3 随机时空地震荷载的埋地压力管道的动力响应

由2.2节可知，埋地压力管道仅在压力作用下会产生周向应力σφ和轴向应力σx，那么，当轴向应力σx与地震荷载下管道轴向应力σe共同作用时，管道轴向应力σ1为：

σ1=σx+σe

(15)

当轴向应力σx，周向应力σφ，径向应力σr与地震荷载下管道轴向应力σe共同作用时，如图6所示，利用von-Mises屈服条件得管道应力σs为：

2σs2=(σ1-σφ)2+(σφ-σr)2+(σ1-σr)2

(16)

因管道为薄壁构件，径向应力可忽略不计，即：

σr=0

(17)

因上述3个截面内无剪力，故σφ，σx，σr分别为3个主应力。则：

(18)

因此，由式(13)、式(15)可得，σs为：

(19)

3 非概率可靠性

3.1 区间可靠性

设结构的功能函数Z为

Z=R-SZ=g(x)=g(x1,x2,…,xn)

(20)

式中：R代表结构抗力；S代表载荷作用效应。当Z>0时，结构是安全的；当Z<0时，结构是失效的；当Z=0，代表结构处于极限状态。对不确定参数进行区间处理，设不确定参数x=[a,b]，则利用区间中点xC和区间半径xR来反映模型的几何特征：

对参数进行标准化变换：

κ=xC+xRγ

(21)

式中：γ为标准化的区间变量。

代入功能方程式(20)可得：

Z=RRγR-SRγS+(RC+SC)

(22)

式中：RR为应力的区间半径；SR为强度的区间半径；RC为应力的区间中点；SC为强度的区间中点。

当Z为线性或非线性功能函数时，β的物理意义为标准化区间变量的扩展空间里，以无穷范数‖‖∞度量从坐标原点到失效面的最短距离。

基于区间模型的非概率可靠指标β定义为：

(23)

式中：ZC为功能函数中点；ZR为功能函数半径。

3.2 埋地压力管道非概率可靠性模型

埋地压力管道的极限状态功能函数一般形式为：

Z=g(x)=g(x1,x2,…,xn)

(24)

对于埋地压力管道在非随机过程地震荷载下的极限状态功能函数为：

Z(t)=σr-σs(t)

(25)

式中：σr为埋地压力管道的极限应力值；σs(t)为埋地压力管道随时间变化的应力值。

将其中的不确定参数处理为区间模型，则根据区间运算的性质[27]，则功能函数Z为Z=[ZL,ZR]。

式中：ZR为区间变量的上界；ZL为区间变量的下界。

利用非可靠性理论，可定义管道的非概率可靠性指标为：

(26)

当非概率可靠性指标β>1时，则Z>0，此时结构安全可靠；当1<β<1时，则Z>0或着Z<0都有可能，则结构可能安全可能失效，从工程实际上认为，此种情况结构不可靠；当β<1时，则Z<0，此时结构失效[28]。而利用β的值可以评价管道的安全程度，β的值越大就表明管道的安全程度越高。

4 非随机过程下压力埋地管道应力强度分析

本文以某成品油管道为例，分析其在非随机过程下的应力强度，并进行非概率可靠性分析。参考文献[24]，选取该管段中的200 m进行分析。管径为457 mm，管材为X60，设计压力为10 MPa，标称壁厚为8.7 mm，弹性模量为207 GPa，泊松比为0.3，屈服应力区间为[389，423] MPa，剪切波速取为283 m/s2，管道的轴向刚度为1.28×109N/m2，周围介质的刚度为9.52×107N/m2，场地土的加速度区间为[-4.671，3.417] m/s2。此时为平稳区间过程，XR(t)为0.627 m/s2，XC(t)为4.044 m/s2。在很多实际问题中，激励的解析表达式难以获得，故本文以埋地管道为例提出求解场地位移的方法作为场地轴向位移的依据，即：

根据GB 50470-2008《油气输送管道线路工程抗震技术规范》[29]。

当只考虑一维运动时，假定地震波为剪切波，即：

(27)

式中：Tg为地震动反应谱特征周期，根据现行国家标准《中国地震动参数区划图》(GB 18306)获取。

土体中将其进行非平稳化可得：

(28)

C参照文献[18]统计分析取值，C=0.3；t1=5 s；t2=10 s。

则载荷的非平稳随机过程如图7所示：

图7 地震荷载的非平稳区间过程Fig.7 Non-stationary interval process for earthquake load

则场地位移的区间为：

(29)

根据文献[30]，该函数为非线性关系，即需建立数学优化模型求解此函数的上、下界：

(30)

s.t. -0.03≤ug≤0.02

根据式(30)，利用优化工具，求解出，地震作用下应力区间[-31.05，20.70] MPa，根据第四强度理论，可得[229.63，242.28] MPa。

参数的区间数为：

xC=235.96;xR=6.33

即可建立功能函数：

Z=σr-σs

(31)

将其标准化为：

Z=17γr-6.33γs+170.05

区间非概率可靠性指标为：β=7.29>>1。

区间可靠性模型计算的非概率指标大于1，即结构的失效域和安全域不相交，如图8。说明该结构可靠，且无量纲的β越大，结构的安全程度越高。

图8 位移区间Fig.8 Displacement’s interval chart

5 有限元模拟

5.1 基本参数

本文以Abaqus作为有限元计算软件。采用非线性的面-面接触来建立管土相互作用三维有限元模型，刚度大的管道外壁选为主表面，刚度小的土体选为从表面，法向接触行为采用“罚”接触，摩擦系数选用0.5。管道由实体单元模拟，埋深为3 m。土体由实体单元模拟，本构关系为Drucker-Prager(D-P)模型。材料基本参数见表2。

表2 材料基本参数Table 2 Material’s basic parameters

5.2 有限元模型

模型中管道远端仅约束轴向位移。土体施加载荷的两对称表面、上表面自由，其他面均为对称约束。选用8节点线性六面体减缩积分单元(C3D8R)[31]。模型的网格划分如图9所示。

图9 网格划分Fig.9 Divide grid diagram

图10 上边界载荷下的von-MisesFig.10 Von-Mises diagram under upper boundary load

图11 下边界载荷下的von-MisesFig.11 Von-Mises diagram under lower boundary load

有限元分析结果表明，基于实际工程中地震贫数据的情况，对地震荷载进行非平稳性区间过程(非随机过程)的处理是合理的，且是针对地震荷载的随机过程的补充。

6 结论

1) 在只有小样本的工程地震分析中，建立了非平稳区间过程的地震荷载。这对于实际工程设计来说，建立地震荷载响应边界更易于随机振动分析在工程上的推广。

2) 利用管道动力求解中的级数解法简化了地震作用下埋地管道的动力特性的求解。

3) 在无法建立概率密度函数和隶属函数函数的情况下，即传统的概率可靠性分析结果不可信的前提下，建立了以埋地压力管道的非概率凸集合可靠性分析的模型。

4) 利用凸模型理论得出埋地压力管道在非平稳区间过程激励下的非概率可靠性指标，是对管道结构的概率可靠性分析的补充，为建立长输成品油管道在非随机荷载作用下的非概率可靠性分析奠定了基础，对于结构评估及可靠性设计具有重要的工程意义。

[1] 朱位秋.随机振动[M].北京：科学出版社，1992.

[2] 刘章军.基于随机振动理论的抗震分析方法研究进展[J].地震工程与工程振动，2006，26(4)：47-51.

LIU Zhangjun. Research progress of seismic analysis method based on stochastic vibration theory [J]. Earthquake Engineering and Engineering Vibration，2006，26(4)：47-51.

[3] 张庆飞.一种新型非概率凸模型及相应的结构不确定分析技术[D]. 长沙：湖南大学，2013.

[4] 刘宁宇. 非随机过程模型及非随机振动分析[D].长沙： 湖南大学，2016.

[5] BENHAIM Y. Convex models of uncertainty in radial pulse buckling of shells [J]. Journal of Applied Mechanics，1993，60(3)：683-688.

[6] ELISHAKOFF I. Whys and hows in uncertainty modelling [J]. Information Processing & Management，1985，21(6)：V-XV.

[7] BEN-HAIM Y. A non-probabilistic measure of reliability of linear systems based on expansion of convex models[J]. Structural Safety, 1995, 17(2): 91-109.

[8] 欧进萍，王光远．基于模糊破坏准则的抗震结构动力可靠性分析[J]．地震工程与工程振动，1986(1)：1-11.

OU Jinping，WANG Guangyuan. Dynamic reliability analysis of seismic structure based on fuzzy failure criterion [J]. Earthquake Engineering and Engineering Vibration，1986(1)：1-11.

[9] 王光远，欧进萍．结构模糊随机振动的理论与应用[J]．地震工程与工程振动，1992(3)：16-25.

WANG Guangyuan，OU Jinping. Theory and application of structural fuzzy random vibration [J]. Earthquake Engineering and Engineering Vibration，1992(3)：16-25.

[10] 欧进萍，王光远，汪培庄.模糊过程与模糊微分方程的解法[J].模糊系统与数学，1991(2)：1-10.

OU Jinping，WANG Guangyuan，WANG Peizhuang. Solution of fuzzy processes and fuzzy differential equations [J].Fuzzy Systems and Mathematics，1991 (2)：1-10.

[11] KANG Z, LUO Y, LI A. On non-probabilistic reliability-based design optimization of structures with uncertain-but-bounded parameters[J]. Structural Safety, 2011, 33(3): 196-205

[12] GUO S X, LI Y. Non-probabilistic reliability method and reliability-based optimal LQR design for vibration control of structures with uncertain-but-bounded parameters[J]. Acta mechanica sinica, 2013, 29(6):864-874.

[13] 邵世飞，周昌玉，常乐.压力管道应力强度非概率可靠性分析[J].南京工业大学学报(自然科学版)，2016，38(3)：44-49.

SHAO Shifei，ZHOU Changyu，CHANG Le. Analysis of non-probabilistic reliability of stress intensity in pressure pipelines [J].Journal of Nanjing University of Technology (Natural Science Edition)，2016，38(3)：44-49.

[14] 刘次华. 随机过程及其应用[M]. 3版.北京：高等教育出版社，2004.

[15] 邱志平.非概率集合理论凸方法及其应用[M].北京：国防工业出版社，2005.

[16] AMIN M. Nonstationary stochastic model of earthquake motions[J]. Journal of Engineering Mechanics.ASCE, 1968, 94.

[17] DAVENPORT A G. Note on the distribution of the largest value of a random function with application to gust loading[J]. Proceedings of the Institute of Civil Engineers, 1964, 28(2): 187-196 .

[18] 陈永祁，刘锡荟，龚思礼. 拟合标准反应谱的人工地震波[J]. 建筑结构学报，1981，2(4)：34-43.

CHEN Yongqi，LIU Xihui，Gong Sili. Artificial seismic waves fitting the standard response spectrum [J]. Journal of Architectural Structure，1981，2(4)：34-43.

[19] LEE D H, KIM B H, LEE H, et al. Seismic behavior of a buried gas pipeline under earthquake excitations[J]. Engineering Structures, 2009, 31(5):1011-1023.

[20] QU T J, WANG J J, WANG Q X. A practical model for the power spectrum of spatially variant ground motion[J]. Acta Seismologica Sinica, 1996, 9(1):69-79.

[21] JIANG C, NI B Y, HAN X, et al. Non-probabilistic convex model process: A new method of time-variant uncertainty analysis and its application to structural dynamic reliability problems[J]. Computer Methods in Applied Mechanics and Engineering, 2014, 268(1): 656-676.

[22] 翟贺，李鹏程，李志明. 地震行波作用下埋地管道弯曲变形分析[J]. 防灾减灾学报，2014(1)：16-19.

ZHAI He，LI Pengcheng，LI Zhiming. Analysis of bending deformation of buried pipeline under seismic traveling wave[J]. Journal of Disaster Preparedness and Prevention，2014(1)：16-19.

[23] 梁瑞，马东方，俞树荣，等．埋地管道在地震载荷作用下的动力响应分析[J]．石油机械，2007，35(12)：16-18, 94-95.

LIANG Rui，MA Dongfang，YU Shurong，et al. Dynamic response analysis of buried pipelines under earthquake loads[J]. Petroleum Machinery，2007，35(12)：16-18, 94-95.

[24] 屈铁军，王前信. 地下管线在空间随机分布的地震作用下的反应[J]. 工程力学，2003，20(3)：120-124.

QU Tiejun，WANG Qianxin. The response of underground pipelines under random spatially distributed earthquakes [J]. Engineering Mechanics，2003，20(3)： 120-124.

[25] 屈铁军，王前信. 地下管线多点地震激励纵向振动的级数解[J].地震工程与工程振动，1993(4)：39-46.

QU Tiejun，WANG Qianxin. Series solution of multi-point seismic excited longitudinal vibration in underground pipelines [J]. Earthquake Engineering and Engineering Vibration，1993(4)：39-46.

[26] 张鹏．在役原油长输管线剩余工作能力研究[D]．哈尔滨：哈尔滨建筑大学 哈尔滨工业大学，1997.

[27] 郭书祥，吕震宙，冯元生. 基于区间分析的结构非概率可靠性模型[J]. 计算力学学报，2001，18(1)：56-60.

GUO Shuxiang，LYU Zhenzhou，FENG Yuansheng. Structural non-probabilistic reliability model based on interval analysis [J]. Chinese Journal of Computational Mechanics，2001，18(1)：56-60.

[28] 魏宗平. 在役腐蚀管道动态非概率可靠性分析[J]. 工程设计学报，2014，21(1)：27-31.

WEI Zongping. Dynamic non-probabilistic reliability analysis of corroded pipelines in service [J]. Journal of Engineering Design，2014，21(1)：27-31.

[29] 中华人民共和国住房和城乡建设部.油气输送管道线路工程抗震技术规范：GB 50470-2008 [S].北京：中国计划出版社，2009.

[30] 王晓军，王磊，邱志平.结构可靠性分析与优化设计的非概率集合理论[M].北京：科学出版社，2016.

[31] 赵潇.采空沉陷区埋地管道应力变形分析及远程检测[D].成都：西南石油大学，2015.