改进拉伊达准则在LabVIEW温度采集系统中的应用
,,
(1.杭州电子科技大学 计算机学院,杭州 310018; 2.浙江省计量科学研究院,杭州 310016)
0 引言
在常见的数据采集系统中,采集到的数据通常包含较大的误差,误差虽然是被允许的,但是粗大误差(也称为野值)的出现会大大影响测量结果的准确性,所以在测量得到一系列数据之后需要对粗大误差进行剔除,来保证测量结果的准确性。粗大误差的出现通常是因为检测环境受到外界的干扰或者是实验者的粗心大意引起的。常见的粗大误差剔除方法有格拉布斯准则、迪克逊准则、拉伊达准则等[1]。格拉布斯准则和迪克逊准则适用于测量样本数较小时使用、计算公式复杂,在使用时需要查表;拉伊达准则由变化的贝塞尔公式推导而来,使用时简单方便,适用于测量样本数较多的场景。在本系统中,温度是一种迟滞性的缓变量,随着不断加热,温度会不断线性缓慢上升直到目标温度,为了实时准确地监控温度的变化,要频繁的对整个过程进行数据采集,所以拉伊达准则在本系统中比较适用。
LabVIEW是Laboratory Virtual Instrument Engineering Workbench的缩写,是一款使用图形符号来编写程序的编程环境,具有开发周期短、界面美观大方、灵活方便、跨平台等特性[2]。LabVIEW编程开发环境与常见的C、Java等开发环境有一个重要的区别是:LabVIEW是使用图形的编程语言,而不是使用文本进行编辑。一个VI界面可以分为前面板和程序框图两部分,前面板是VI的交互式图形用户界面,模拟了物理仪器的面板,可以有按钮、温度计、波形等显示控件和输入控件,且这些控件还能与Photoshop等图片优化软件结合使用,使界面更加美观大方[3]。程序框图是VI的源代码,类似于面向对象语言的类,由LabVIEW的图形化编程即G语言构成,是实际可执行的程序。程序框图由子VI、库函数、控制结构和常量、对象等构成,用连线将对象连接起来定义它们之间的数据流。对象对应着前面板的终端,这样就可以实现用户和后台程序的交互[4]。由于LabVIEW的以上特性,所以LabVIEW具有开发周期短,适合于实验研究场景等优点[5]。
1 常见粗大误差剔除方法
剔除粗大误差的常见方法有格拉布斯准则,迪克逊准则、拉伊达准则等[6],这几种准则的应用都是以检测样本服从正太分布为前提的,以下内容将进行简单介绍。
1.1 格拉布斯准则
使用格拉布斯准则对测量样本T进行粗大误差剔除的步骤如下:
1)计算升序数列的平均值μ和标准差σ;
2)以平均值μ为基准计算计算可疑数据的偏离值Vd,其中偏离值最大的为|Vi|max;
3)根据查表所得的置信概率α和测量次数n,确定临界统计系数g(α,n);
4)若|Vi|max>g(α,n),则认为xi为粗大误差数据,应当剔除,否则认为序列T中不含粗大误差数据,剔除完毕;
5)剔除某一粗大误差后继续执行1)~5),直到没有粗大误差为止。
以上步骤以流程如图1所示。
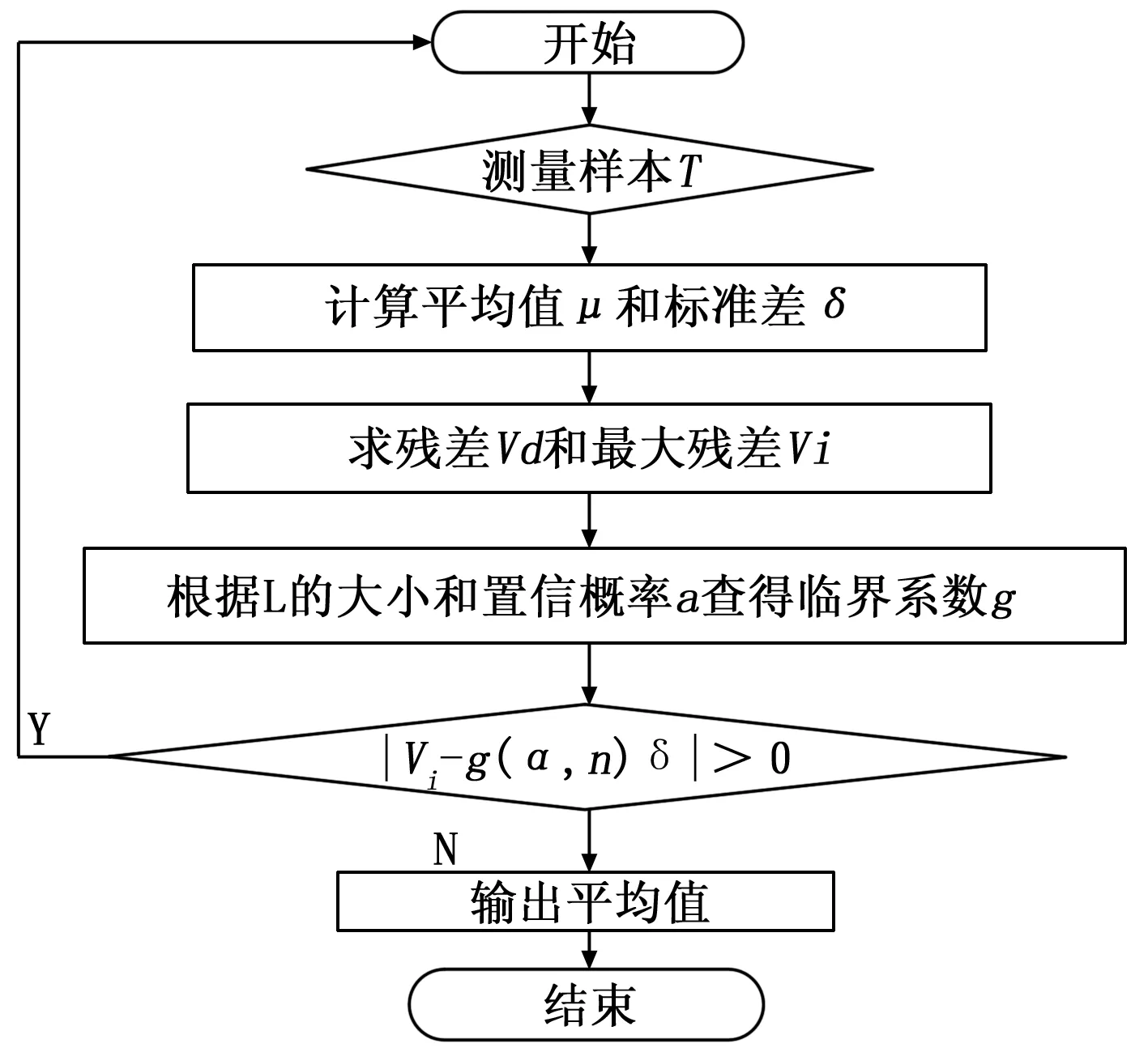
图1 格拉布斯准则流程图
1.2 迪克逊准则
迪克逊准则是一种利用极差比双侧检验来判别粗大误差的方法,可以不用计算采集数据的平均值、标准差和残差,简化了计算过程,但是需要查表[7]。这种方法对于序列中只有一个粗大误差值的测量数据效果较好,但是对于在同侧存在多个粗大误差值时检测效果不佳。其检测步骤如下:
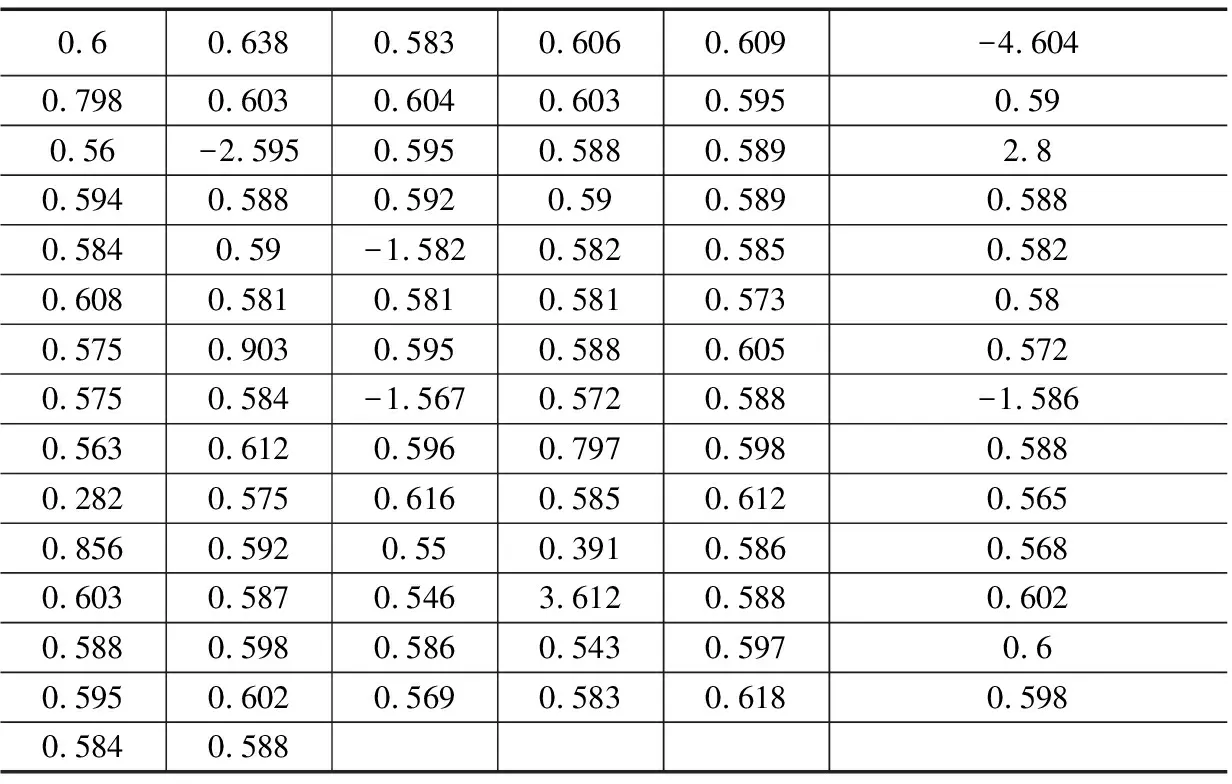
1)将采集数据规模为n的数据从小到大进行排序[2]形成待检测序列T:t1 2)对待检测序列观察待检测值是最大值还是最小值,如果是最大值,则构造统计量: (1) 如待检测值是最小值,则构造统计量: (2) 3)查看迪克逊准则给出的这些统计量的分布函数以及临界值D(α,n)[6],则: P(y22>D(α,n))=α (3) 拉伊达准则是一种依靠测量数据三倍标准差为极限标准取舍测量值的方法,其给定的置信率是99.73%,是一种适用于测量次数较多(n>15)的场景或者是经过大量重复测量已经统计出标准差σ的情况。同时,在文献[9]中,作者提出了一种基于拉伊达准则进行目标值预测的方法,发现将拉伊达准则用于测量数据较多的目标预测场景时也能得到较好的结果。使用拉伊达准则对规模为n的测量数据T进行误差剔除的一般步骤如下: (4) 2)根据均值求出残差: (5) 3)根据残差求出标准偏差: (6) 5)计算n-1个测量数据的均值、残差、标准偏差继续执行(1)~(4),直至没有粗大误差时停止。 δi=ti-to (7) 平均值: (8) 残差: (9) 推导变化的贝塞尔公式可以得出的标准偏差如下: (10) 一般温度采集系统由采集对象、测温热电阻作为传感器、温度采集回路和温度采集软件组成[11]。 在本实验系统中,采集对象是RTS-35A恒温水箱,RTS-35A恒温水箱是一款可按照恒定功率进行加热或者降温的设备,其升温和降温过程一般是按照某一斜率线性上升或者线性下降。测温热电阻是温度系统中重要的传感器,将被测对象的温度以电阻的形式反应出来,然后交由温度采集回路进行处理。温度采集回路是将测温热电阻的值传送至温度采集软件进行分析和处理,在本系统中,温度采集回路使用的是Agilent34970A进行采集,Agilent34970A的精度为六位半,有精确的测量能力,可以应用于各种场合。Agilent34970A使用两种标准通讯接口:GPIB(IEEE-488)、RS232,GPIB接口具有通讯质量高性能稳定等优点,但是PC机没有GPIB接口,而且GPIB接口通信距离短等缺点使得GPIB接口不适用用本系统,本系统采用RS232接口协议进行通信。温度采集软件使用虚拟仪器语言Labview来实现[12]。本系统结构如图2所示。 图2 温度采集系统结构图 在本系统中,利用Agilent34970A六位半采集仪来对采集到的电阻值进行转换,再上传到上位机Labview程序中,Agilent34970A与上位机的通讯是采用SCPI(可编程仪器控制命令)进行,上位机发送“read?”指令给采集仪,采集仪就会返回所有通道的数据。Labview上位机采集数据使用VISA串口通信方式,VISA是应用于仪器编程标准I/O应用程序接口(API),是可以调用底层驱动器的API,Labview在使用的时候也要安装相应的驱动程序[13]。 采集数据可以分为五步,第一步上位机写入“read?”指令到端口;第二步是等待延时时间保证能收到缓冲区里面正确的数据;第三步是从端口中读出数据;第四步是对读出的数据进行处理和显示;第五步采集结束后将采集到数据导入到excel文档中。其程序如图3所示。 图3 采集程序程序框图 图4是利用改进拉伊达准则进行野值剔除的程序框图,程序在实现的过程中先去Excel表格中读取测量样本,存到原始数据数组中。取到测量样本后,对原始数据数组利用改进拉伊达准则进行处理。 处理步骤可以分为5个部分: 1)对原始数据进行累加得到累加值,初始化ti-t0和(ti-t0)2数组; 2)利用累加值求出算术平均值,在本实验中,经过多次取值计算发现初始值t0选择为平均值时能得到最好的结果; 3)求得ti-t0和(ti-t0)2数组; 4)利用ti-t0和(ti-t0)2数组分别求出ti-t0和(ti-t0)2数组的和放在临时变量1和临时变量2中;图4为利用改进拉伊达准则剔除粗大误差的前四步程序框图。 图4 改进拉伊达准则剔除粗大误差程序框图 5)设置一个while loop循环,在循环体里面利用前4步求得的临时变量对测量样本进行粗大误差剔除,首先根据临时变量1、临时变量2、预估计值求出平均值和标准偏差的3倍,并把剔除完成标记置为0,接下来利用一个for loop循环对数据进行实际操作,利用原始数据减去平均值和标准差的3倍进行比较看是否是粗大误差值,如果该值为粗大误差值,粗大误差数+1,临时变量1和临时变量2分别减去ti-t0数组、(ti-t0)2数组中位置为i的元素,并把原始数组位置为i的元素替换为平均值,并把剔除完成标记置为1,表示剔除没有完成,还要进行下一轮的剔除,直到剔除完成为止。图5是利用改进拉伊达准则剔除粗大误差第五步程序框图。 图5 改进拉伊达准则剔除粗大误差程序框图 对采集对象恒温水箱进行设置,采集了从30 ℃上升到80 ℃的温度,每隔500 ms采集一次,得到了数据每个时间间隔温度上升为0.061 ℃左右,对其中的数据按每100个提取一个的方法进行提取得到表1的数据作为原始数据。 表1 采集原始数据 ℃ 在实际应用中,利用拉伊达准则进行数据处理时,要求被测数据稳定在某个值附近,满足正态分布;对于波动特别大的数据,就判定其为粗大误差。在本实验系统中,温度是一种带有迟滞性的研究对象,其单位时间温度上升是一个平滑的过程,对表1的数据进行分析,发现数据处于一个基本稳定上升的过程中,原因是恒温加热水箱通过某一恒定功率进行加热,其特点是在单位时间内温度的增量波动不大。可以通过表1得到其单位时间内温度增量表表2,可以看出是符合前面提到的温度单位时间内上升0.061 ℃的要求的,为了进一步的验证改进拉伊达算法在本实验中可行性,在原始数据中加入毛刺数据,共加入7个,得到表3的数据。对表3的数据进行减法分析处理得到单位时间的增量表表4。 表2 原始数据增量表 ℃ 表3 毛刺数据表 ℃ 对表4的数据通过图4、5的Labview程序进行处理,共循环两次,发现加入的7个毛刺数据为粗大误差值。第一次处理时得到平均值为0.482221,3倍的标准偏差值为2.616408,剔除了第6、13、68位毛刺数据;第二次循环得到平均值为0.541301,3倍标准偏差值为2.054999,剔除了第18、27、45、48位毛刺数据。至此,毛刺数据剔除完毕,第三次循环时平均值为0.538886,3倍标准偏差值为2.106758,发现无粗大误差,剔除过程结束。 表4 毛刺数据增量表 ℃ 通过分别比较剔除前和剔除后增量数据表与原始数据表,见图5、6,可以发现原用于对稳定数据进行粗大误差剔除的拉伊达准则,对于增量数据的粗大误差剔除,也能取得良好的效果,在保证漏剔率和误剔率的同时,还可以保证得到较为准确的实验结果,对于后续的实验分析具有很大的帮助。 图5 增量数据剔除前后对比 图6 原始数据剔除前后对比 在工程的实际设计和测量过程中,灵活的运用LabVIEW进行开发可以大大的缩短开发周期和节约人力成本,也可以方便地构建直观的虚拟仪器界面。在基于LabVIEW设计的采集测量平台中,进一步改进了拉伊达准则,将其应用在稳定持续变化的温度测量场合,扩大了其应用范围。实验表明,改进使用后的拉伊达准则可以准确的对试验产生的粗大误差进行剔除,大大提高了试验数据的准确性,确保测试结果可信性,在后期涉及到多数据的采集中具有良好的实用意义。 参考文献: [1] 卢元磊,何佳洲,安 瑾. 几种野值剔除准则在目标预测中的应用研究[J]. 指挥控制与仿真,2011,33(4): 98-102. [2] 王中宇,刘智敏,夏新涛. 测量误差与不确定度评定[M]. 北京: 科学出版社, 2008. [3] 张 敏. 拉依达(Pau θ Ta)准则与异常值剔除[J]. 郑州工业大学学报. 1997,18(1):84-88. [4] 熊艳艳,吴先求.粗大误差四种判别标准的比较与应用[J].大学物理实验,2010:66-68. [5] 覃 欣, 熊 娟.LabVIEW数据处理中3σ准则的应用[J].中国测试, 2009,35(5): 66-69. [6] 孙培强.正确选择统计判别法剔除异常值[J]. 计量技术, 2013,11(12):71-73. [7] Zhang P Z. Design of hierarchical fuzzy PID controller based on Granular computing in LabVIEW[A].2009 Sixth International Conference on Fuzzy Systems and Knowledge Discovery[C].Tianjin, 2009. [8] 安海超, 杨人凤, 杨 波. 基于LabVIEW的纤维投料机非线性偏差校正[J]. 北京工业大学学报, 2016,42(11):1713-1719. [9] 陈亚斌, 王亚刚, 周代仝. 基于修正狄克逊准则的多传感器融合算法[J]. 通信技术, 2014,47(10):1178-1182. [10] Zhao J P, Liu X F.Research on PID controller for Hydraulic Servo System based on LabVIEW[A]. 2015 International Conference on Fluid Power and Mechatronics[C].Harbin, 2015. [11] 郑 峰, 王 睿, 宦克为. 粳米近红外光谱模型中基于拉依达准则的异常值剔除方法[A]. 第十七届全国分子光谱学术报告会[C].广东, 2012. [12] JunqinLlU S J. Design on the central air-conditioning controller based on LabVIEW[A]. 2010 International Conference on Computer Application and System Modeling (ICCASM 2010) [C].Taiyuan, 2010. [13] Panchal P, Patel A, Barve J.PI Control of Level Control System using PLC and LabVIEW based SCADA[A]. 2015 International Conference on Industrial Instrumentation and Control (ICIC)[C]. College of Engineering Pune, India,2015.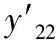
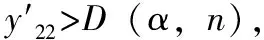
1.3 标准拉伊达准则

1.4 改进的拉伊达准则

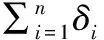
2 系统设计与实现
2.1 系统基本组成
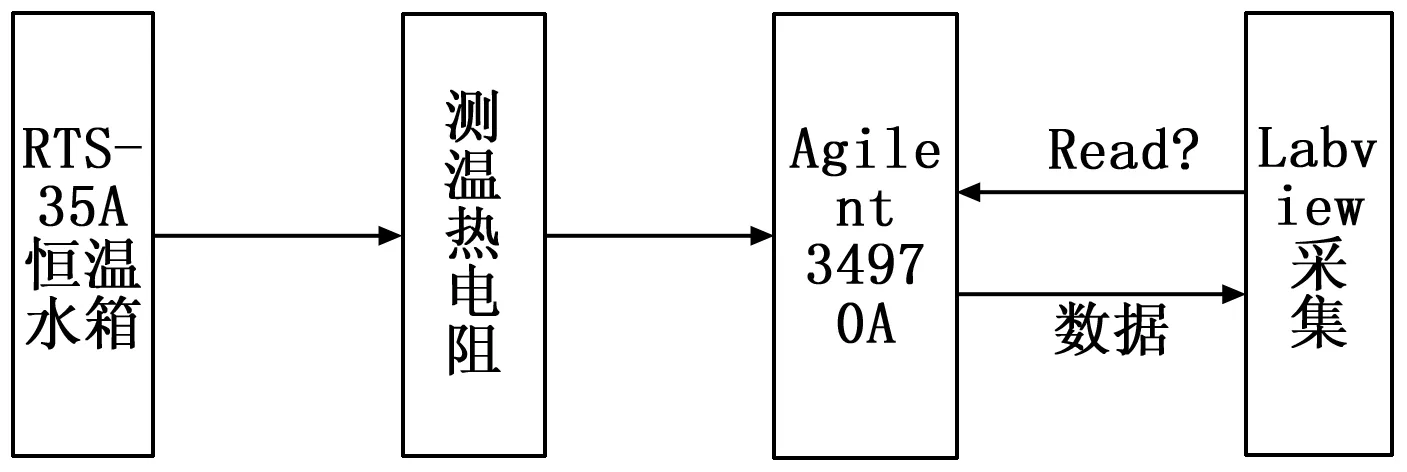
2.2 系统采集详细设计
2.3 利用改进拉伊达准则进行数据处理



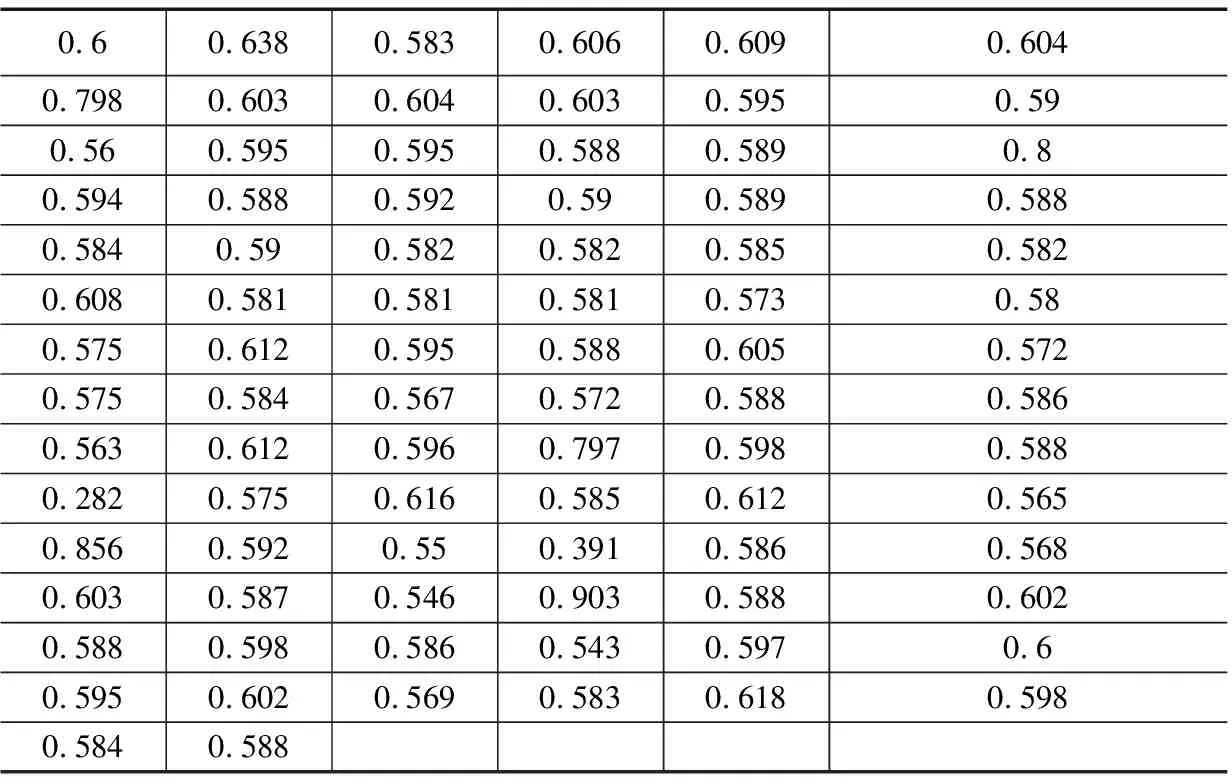
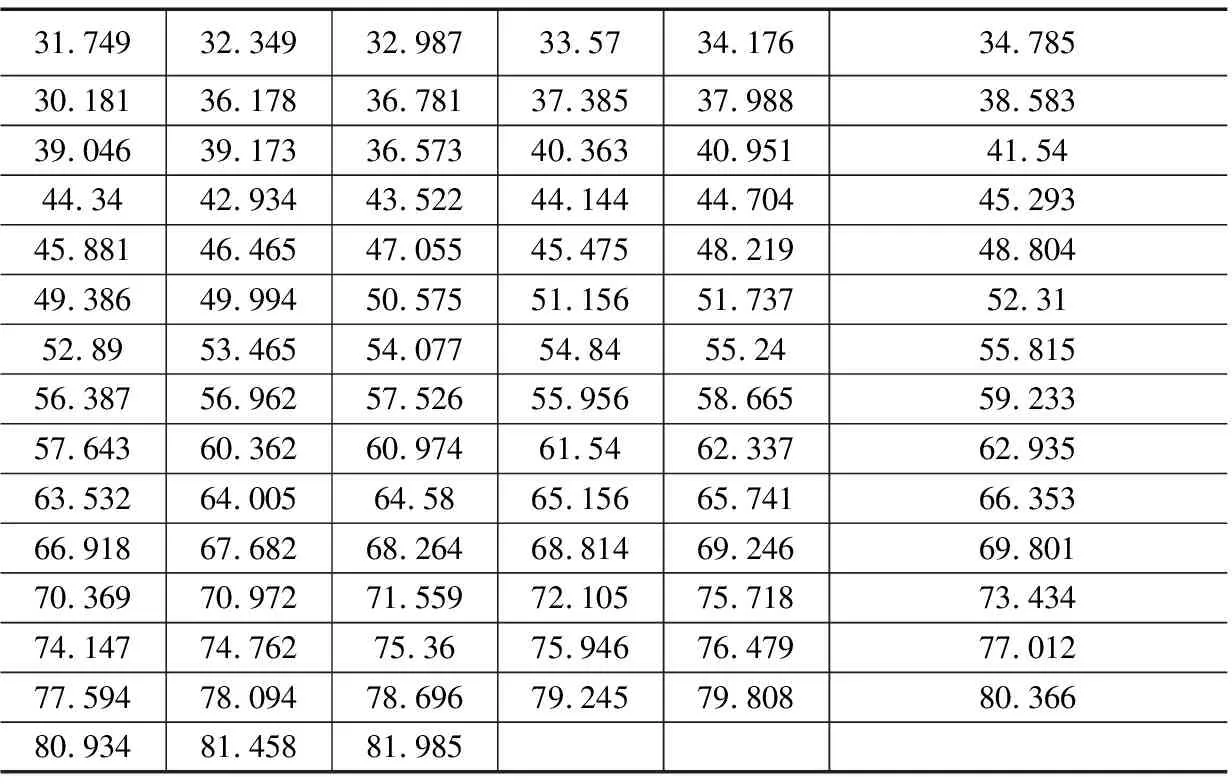
3 结论



