城轨车辆辅助逆变器IGBT状态识别研究
,,,,
(1.上海工程技术大学 城市轨道交通学院,上海 201620; 2.上海地铁电子科技有限公司,上海 200233)
0 引言
辅助逆变器是地铁车辆车辆的重要组成部分,它为车内照明、空调、通风机等除牵引系统外的设备提供电源。辅助逆变器故障将影响列车安全、稳定运行,在地铁车辆故障统计中,辅逆系统故障率第一,尤其是以IGBT发生故障后果突出。小波分析是一种信号的时间-频率分析方法,它有在时域和频域都有表征信号局部特征的能力,相较于傅里叶分析更适合处理此类诸如IGBT故障引起的非平稳信号,它能通过对信号的伸缩或平移来逐步进行目标信号的多尺度细化[1],从而能准确找到故障点,能有效地检测出故障,但不能直接从波形上进行故障状态识别。因此当故障的程度很小,如器件发生参数性故障时,使用小波变换所得的信息是很有限的[2],这些信息用于电路故障识别,特别是软硬故障的识别是困难的,而马氏距离可有效弥补这一不足。马氏距离表示数据的协方差距离,它能考虑到具有多特征样本之间的联系,是一种能有效的计算样本集之间相似度的方法[3],能够从数据上直观的反映出和正常样本之间的差距,从而进一步实现电路故障状态的识别。本文从城轨车辆辅助逆变器主电路出发,全面考虑其中IGBT的软硬故障,提出一种小波分析与马氏距离结合的新电路状态识别方法,并通过重复大量实验证明该方法的可行性,且能够良好适用于地铁辅助逆变器的状态识别,判断过程简单有效。
1 电路分析
1.1 辅助逆变器主电路仿真
地铁辅助逆变供电系统是将来自地铁受电弓或第三轨输入的DC1500V或DC750V电压经辅助逆变后转化为三相交流电输出供给 负载,其中辅助逆变电路是核心组成部分,由输入电路,逆变电路,输出电路组成,其主电路原理如图1所示,电路图由一个1500 V的直流电源、三相桥式逆变电路和负载组成。
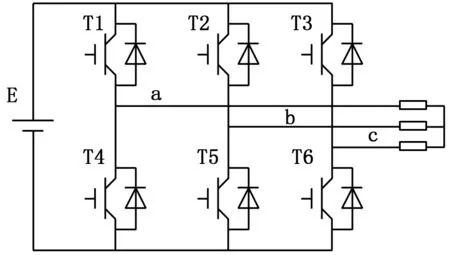
图1 辅助逆变器电路原理图
1.2 逆变器电路状态分析
电力电子电路故障可分为参数性故障和结构性故障两种。参数性故障也称为软故障[4],是指电路元件在参数上(如电阻、电感、电容值)偏离正常值(一定范围内)而产生的故障,此时电路大多能正常工作,不会严重影响系统输出,因此很难发现电路存在故障,但存有安全隐患。当元件参数偏离超出一定范围时,软故障转化为硬故障,这时电路系统结构发生变化,导致电路运行故障并且严重时造成车辆运行故障,所以对软故障的研究十分必要,能尽可能排除车辆的运行隐患。本文根据文献[5]提出的当IGBT 管压降超过正常值的±15%作为软故障临界状态依据,通过在T1发射极加电阻R改变管压降进行软故障模拟,经仿真分析得软故障临界值对应的R为26 Ω。结构性故障[6]是指由于器件出现短路、开路等故障而导致电路的拓扑结构发生变化,一般IGBT在发生硬故障的前期有一个隐患状态,表现为内阻的增大,当内阻增大到一定值时就会表现为开路状态致使电路无法正常工作。因此本文在模拟IGBT开路硬故障时,采用相应IGBT门极信号丢失的方式来实现,即不给相应IGBT的门极加占空比信号。
根据图1在Matlab构建电路模型进行仿真,其中输入电压为1 500 V,IGBT门极脉冲宽度调制频率为50 Hz,采用Matlab中正弦脉宽调制器SPWM来进行调制。仿真时为了更为接近实际电路,负载采用Simulink模块中的“Three-Phase Series RLC Load”模块,直接加载50 Hz的2 400 W的有功功率。图2分别是IGBT正常情况、单个IGBT软故障、硬故障(均以T1为例)对应的输出端电流波形。从图中可以看到电路在正常情况下输出对称的三相交流正弦波,软故障虽然波形相交于正常状态下的正弦波有略微波动,但依旧是三相的正弦波,不会对实际供电造成大的影响,而硬故障a相波形相较于正常情况下明显发生畸变,表明电路已不能正常运行,电路严重故障。

图2 辅助逆变器输出电流波形图
2 小波包分解
2.1 T1处a相信号的小波包分解
在正交小波分解过程中,一般是将低频系数分解为两部分。分解后得到一个低频近似频段和一个高频细节频段。在两个连续的低频近似频段中丢失的信息可以在高频细节频段中得到。下一步是将低频近似频段进一步分解为两个高频和低频部分,而高频细节频段不再分解。为了克服小波分解在高频段的频域分辨率较低,而在低频段的时域分辨率较差的缺点[7],在小波分解的基础上提出了小波包分解。它不仅能够对低频信号进行较好时频域分解,高频信号也能同等处理,提高了信号在频域上的分辨率,是一种更为精细的信号分析方法。小波包分解中,一维情况下和小波分解同样信号被分解成高频细节段和低频近似段,产生一个二叉树,对应的特征向量为:vector1=[x1,x2];二维情况下分别对上次分解后的高、低频信号再做高低频分解,并产生一个四叉树,对应的特征向量为vector2=[x1,x2,x3,x4],以此类推,在三维情况下就能生成8个不同频段的信号。在辅助逆变电路状态识别时,需要对正常值、软故障、硬故障的a、b、c三相电流信号分别进行小波包分解并提取特征值,组成特征样本。图3是分别对图1电路中T1管在正常、软故障、硬故障(开路)3种状态下对应的a相电流信号进行3层小波包分解后的结果,原始电流信号频率为50 Hz,各层小波包分解后各层频率如表1所示。图3中显示了3层分解后得到的8个不同频率段信号波形图,s130~s137分别是不同频带上的信号波形图,s130体现了信号中频率最低的波形图,即可理解为去除高频干扰因素后的理想状态下电流的波形,s137表示提取信号中频率最高的电流波形图,可以看出对于正常情况下的a相正弦波的小波包分解后高频段波形图都很平稳、幅值不大,说明该信号所处电路状况良好无故障。a相软故障中s130中,信号从0.6秒开始发生软故障,s131之后的波形图幅值增大,说明电路杂质变多,可见单个T1软故障能导致输出电流的不稳定。而硬故障下的a相电流信号个小波包分解频段波形相较于正常情况下幅值明显增大,电路状态故障明显。

表1 小波包分解各层频率表

图3 三层小波包变换波形图
2.2 特征值提取
由于电流信号复杂多变,在诊断时往往出现数据计算量大导致计算复杂,因此处理信号是会对其变换,使之突出该信号特诊并简化之后的计算。特征值提取是信号处理中重要的一步,信号各频带的小波包分析依据Parseval能量积分等式[8]。信号f(x)在时域上的能量公式为:
(1)
小波包分解是线性分解,满足能量守恒公式:
(2)
由上式可知,小波包系数能确定信号各个频段能量的大小,本文中信号经过三层小波包分解为 8 个频段,分别对这 8 段信号进行小波包系数重构,并计算出每段频段能量占总能量的百分比(特征值)作为一个特征向量[9]。表2是电路T1管在正常、软故障、硬故障(开路)3种状态下对应的输出电流各相(a、b、c相)经小波变换后提取的特征向量,其中每种电路状态的a、b、c相的3个特征向量组成一个电路状态样本,为之后的马氏距离做准备。
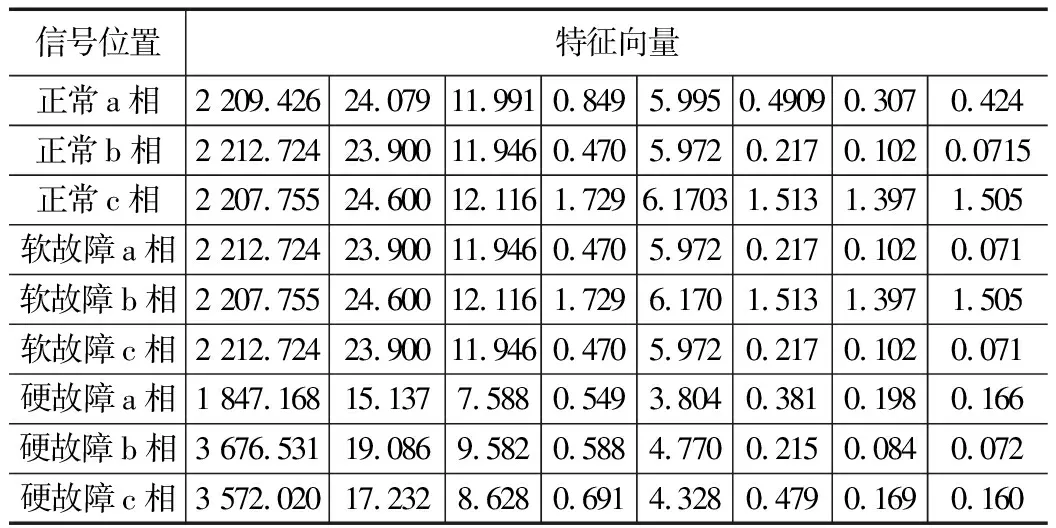
表2 3种电路状态电流信号小波包分解特征值
3 马氏距离
马氏距离是一个能有效地计算样本与样本集的距离和相似度的算法,与欧氏距离相比,它不受量纲的影响,即点与点之间的马氏距离不受数据单位的影响,它考虑到各种性之间的联系并且是与尺度无关的[10],独立于测量尺度。
样本向量y到样本集m×n矩阵之间的马氏距离为:
(3)
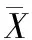
(4)
CX为矩阵的协方差矩阵,定义为:
(5)
本文中利用马氏距离来进行电路状态样本间距离的计算,根据不同故障特征样本与正常情况下样本之间的马氏距离来进行状态识别。其中阈值是根据两个极端情况,即软故障临界值(管压降±15%)和硬故障(单个IGBT开路 )的样本值(表2)分别与电路正常情况的样本之间马氏距离来确定的。其阈值计算结果如表3。
在计算马氏距离的时候,要求总体样本数大于样本的维数,即n>m,否则计算时得到的样本的总体协方差矩阵的逆矩阵不存在,马氏距离无法计算。但在实际应用中“总体样本数大于样本的维数”这个条件是往往是满足的,因此马氏距离可以运用于大量情况下进行顺利计算。
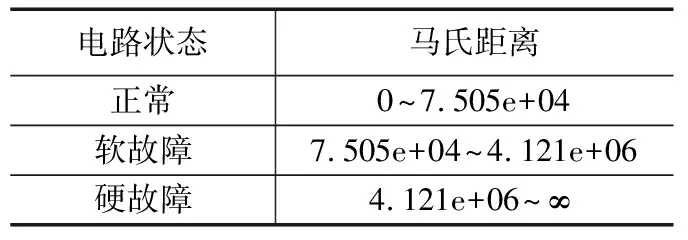
表3 故障阈值表
4 电路状态识别
以图1所示电路为例进行说明。在实际电路状态识别中,取待测电路输出端的三相电流为研究对象,并对其进行小波包分解提取特征向量、组成待测电路样本,再将待测电路样本与正常情况下的电路样本做马氏距离,得到的结果分别阈值对比,即可完成软、硬故障的识别。具体实现过程如下:
1)运行正常电路,提取负载侧三相输出电流信号ia,ib,ic;
2)对正常状态下的电流信号进行3层小波包分解,并对电流信号每相提取特征向量v1=[x1,x2,x3,x4,x5,x6,x7,x8],建立电路正常状态下特征样本[v1,v2,v3]-1;
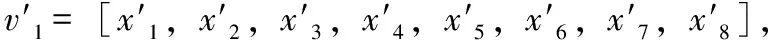
5)将电路正常状态下特征样本与待测电路特征样本进行马氏距离的计算,得到相似度距离D;
6)计算得到的马氏距离D与表3故障阈值表状态区间进行匹配,确定电路状态,完成状态识别。
为了验证小波包分析结合马氏距离的方法在地铁车辆辅逆电路IGBT状态识别中准确性,分别进行多次不同IGBT状态下的待测电路状态识别,重复上述步骤,测得结果后与电路实
际状态相比较,计算正确率。下表4为多次状态识别汇总表,表中的马氏距离表示各待测电路与正常情况下实际计算得到的相似度距离,分别与表3阈值表比较,得到的结果与待测电路实际状态比较符合度,从正确率可见此方法除了在软硬故障临界处有略微偏差外,其余能有效识别IGBT现状。

表4 状态识别汇总表
5 总结
本文提出一种将小波包变换与马氏距离相结合进行地铁辅助逆变电路IGBT状态识别的方法,通过对负载侧输出电流进行特征提取、建立正常状态的特征样本,将不同故障特征样本与正常情况下样本之间的马氏距离匹配来进行状态识别。多次实验表明该方法能够有效应用于地铁车辆辅逆电路IGBT状态识别,该方法能很好地实现软硬故障的区分,简单、运算量小并且应用方便,对于城轨车辆现场维修维护具有重要的参考价值。
参考文献:
[1] 孙丽颖,屈 丹,闫 钿.傅里叶变换与小波变换在信号故障诊断中的应用[N].辽宁工学院学报,2005-6-25(3).
[2] 史秋亮,林 江.基于小波包分解与能量特征提取的相关分析法[J].声学与电子工程,2010,4:18-24.
[3] 盛艳燕,胡志忠.基于小波和马氏距离的电力电子电路故障诊断[J].电子测量技术,2013,36(2):108-112.
[4] 李小波,吴 浩.地铁辅助逆变器滤波电路软故障分析[J]. 电气应用,2012:99-101.
[5] 任 磊,韦 徵,龚春英,等.电力电子电路功率器件故障特征参数提取技术综述[N].中国电机工程学报,2015-6-20(35).
[6] 吴 祎.电力电子电路故障特征参数提取与健康预报研究[D].南京:南京航空航天大学,2013.
[7] Xiong Y L,Cheng X,Shen Z J,et al.Prognostics and warning system for power-electronics modules in electronic,hybrid electric,and fuel-cell vehicles[J].IEEE Transactions on Industrial Electronics,2008,55 (6):2268-2276.
[8] 谭晓东,覃德泽.提升小波包和改进BP神经网络相融合的新故障诊断算法[J].计算机测量与控制,2014,22(8):2405-2408.
[9] 邵占帅,黄 民.基于小波包分解提取刀具振动信号特征向量[J].机械研究与应用,2013,4:58-60.
[10] 葛明涛,董素鸽LMD.及马氏距离敏感阈值的滚动轴承故障诊断[J].机械设计与制造,2015,2:201-213.

