基于相似性算法与蚁群算法的聚类算法

(南京航空航天大学 信息中心, 南京 210016)

0 引言

当今已是大数据时代，随着信息技术的发展，人们积累的音频、视频、文本图片等越来越多，在某些时候需要将这些数据从海量的数据中提取出来，从而将这些数据提供给相关研究人员进行研究和分析。为了将这些不同属性的数据进行正确分类，必须采用聚类算法或分类算法，聚类和分类是机器学习中两种重要的理论和技术，原理上来看聚类技术和分类技术有明显的区别，聚类分析是一种无监督的学习，而分类技术一种有监督的学习[1-9]，聚类分析的智能性要强于其它算法，基于上述理由可以知道聚类分析在大数据时代有着广泛的应用[10-13]。

聚类分析是一种寻找最优解的算法，而粒子群算法，人工蜂群算法以及人工蚁群算法都是一种寻找问题最优解的算法，然而这些仿生物学的智能算法在聚类过程中都有所应用。人工蚁群算法最早是由意大利学者MDorigo提出，该算法在工程领域中主要有如下应用：组合优化问题，网络优化，机器人优化等一系列方面[1-9]。人工蚁群在聚类技术中也有相当的应用: 人工蚁群的觅食过程就是一个寻找问题最优解的过程，因此基于蚁群觅食行为的算法在聚类算法中是最早的应用[1-9]。在2000年Monmarche学者提出了一种混合型的蚁群聚类算法[3-9]，该算法在聚类时容易产生早熟现象，在收敛之前过早的就终止了该算法，这样将造成算法的聚类效果较差等不足之处。人工蚁群在搜索食物源之时，人工蚂蚁都能挥发一种叫做信息素的物质，因此Labroche等相关科研人员根据人工蚁群的这一特征，在2002年提出了一种基于人工蚁群信息素浓度的聚类算法[2-9]，在该算法中人工蚁群，在通过不同的标签来寻找巢穴这一过程，从而实现数据聚类的目的，此算法具有较强的鲁棒性性和较好的适应性，但在算法收敛性这一方面存在一定问题，值得广大科研人员研究。以上是蚁群算法在聚类中有不同的应用，这些算法存在一定的优点，同时也存在某些的不足之处，因此本文在参考了相关的蚁群算法和聚类算法后，提出了一种新的聚类算法，该算法有两部分组成即相似性计算与蚁群算法对聚类中心的选择。

1 什么是聚类分析

聚类分析是一种智能技术，在数据挖掘中是一个重要分支。聚类技术能够对未知数据进行有效的分类，强化机器的智能性，因此各种聚类算法在各个科学领域都有所应用[10-13]。

聚类算法的思想是使用一定的规则将最为相似的数据聚成一个族，然而要求不同族之间的差异性达到最大值，这就是数据的聚类[10-13]。聚类分析进行数据聚类时，在没有训练的条件下能够把对象划分为若干类，这样最相似的数据就聚成了族，因此聚类分析进行数据聚类时是一种无监督的学习。聚类分析中，同一个族中的数据具有较高的相似度，而不同的族数据之间的差异达到最大，这就是聚类的最大特点，在聚类的过程中相似度是聚类经常采用的度量方法。

2 蚁群算法的介绍

2.1 蚁群算法的特点

蚁群算法最初之目的是帮助人们去理解蚂蚁这类物种的复杂行为。蚁群算法出现后不久，便引起了数学家、计算机专家和工程师们的注意，他们把超越生物本身的模型，转换成为一项有用的优化和控制算法，该算法这就是蚁群算法[6-13]。

蚁群在寻找到达食物源的最短路径时，是群体的行为，这些蚁群在路径中都会留下一种叫做信息素的物质，信息素具有挥发性。蚁群之间通过信息素这一物质进行相互交流，从而实现蚁群之间的相互协作和竞争。在路径上的信息素浓度有强有弱，然而蚁群总是向着信息素浓度最高的方向前进。如果路径中的蚁群数量越多，则信息素的浓度就越高，信息素浓度越高，则吸引更多的蚂蚁来到这条路劲中，因此在信息素的协调和作用下，使得整个蚁群都能向着食物源的方向前进。

2.2 蚁群算法的简要分析

蚁群是一个种群，所以蚁群在寻找最短路径过程中是一个群体行为，蚂蚁之间通过相互和协作和竞争来完成共同的目标。当蚁群出发寻找最短路径时，各条路径中的蚂蚁可以在不同的时间点上出发，也可以在同一个时间点上，有若干蚂蚁同时出发。当蚁群搜索算法开始时，寻找最短路径时是蚂蚁的个体行为，但是通过蚁群之间的协调机制和信息素，最终能使得整个蚁群都能找到通往食物源的最短路径。

在蚁群算法中，蚁群之间采用一种分布式的合作机制，蚁群之间的协作性和并行性是其分布合作的具体表现，信息素浓度的大小指引着蚁群寻找通往食物源的最短路径，这是蚁群算法的主要特点。在蚁群算法中人工蚂蚁具有记忆力，因此缩短了蚁群寻找最短路径的时间，从而提高了算法的效率。由于人工蚂蚁具有记忆力，从而蚁群在寻找最短路径时，并不是盲目的搜索，而是有规律、有意识地寻找最优路径，即最短路径。

2.3 蚁群算法的重要参数

β指的是期望启发因子，它反映的是启发式信息在影响蚁群搜索的过程中的相对重要度。β值越大，蚁群就越容易选择局部较短路径，这时算法的收敛速度是加快了，但是随机性却不高，容易得到局部的相对最优。

Q同样是蚁群算法中的一个重要参数，蚁群进行搜索时在路径中能留下不同强度的信息素，不同路径中蚁群挥发的信息素浓度是不同的，如果路径中信息素浓度越大，则Q的值就越大，事实可以证明Q值大小的不同，能对整个蚁群算法产生不同的正反馈功能。算法在正反馈和负反馈的影响下，能够有效地找到问题的最优解。

3 数据的聚类过程

3.1 聚类数据的相似度计算

(1)

分析和讨论：

在3.2经过3.1的数据属性相似度计算后，以下用蚁群算法进行数据聚类中心选择。

3.2 聚类中心的选择与聚类的实现

1)函数：

h(x)=|1-f(x)|

(2)

以上函数讨论如下：

当公式(1):yn=f(x)比值越近于1，则表明数据的相似性更优。数据相似越好，则此时h(x)=|1-f(x)|的值就越小，在采用蚁群算法进行聚类时，聚类数据选择该聚类中心的概率也就越大，此时蚁群启发参数β期望值的相对重要程度也相对越大。

当公式(1):yn=f(x)比值偏离1的程度越明显，则表明数据的相似性更差。数据相似越差，则此时h(x)=|1-f(x)|的值就越大，在采用蚁群算法进行聚类时，聚类数据选择该聚类中心的概率也就越小，此时蚁群启发参数β期望值的相对重要程度也相对越小。

2)在采用蚁群算法进行数据聚类时，聚类公式：h(x)=|1-f(x)|有以下的分析和结论：

(1)蚁群算法聚类时相关参数的说明：

符号di j代表着城市i转移到城市j的距离，每一个城市都是聚类过程中的一个聚类中心。

在选择聚类中心的算法中：设定dij=h(x)=|1-f(x)|。

在聚类中心选择算法中，有两个重要的蚁群算法参数：

参数ηij表示某条路径的能见度程度，反映由城市i转移到城市j的启发程度，通常取值为1/dij。参数β是蚁群算法中的一个重要因子，作为蚁群寻找下一条路径的期望启发因子。β值越大，则人工蚂蚁选择这条路径的概率就也大，并且蚁群越倾向于能见程度高的路径上行走，因此β和ηij的值越大，则人工蚁群选择该路径的概率就越大，该路径上的人工蚁群数量就也就越多。另外在蚁群算法中还以可以证明减小距离，参数β的值也可使该路径被选中的概率增加。

(2)蚁群算法聚类中心的选择：

在本文提出的算法中，一般将数据视为具有不同属性的人工蚂蚁，聚类中心就是蚁群所要寻找的食物源，数据聚类的过程可以被看作是蚂蚁寻找食物源的过程，在这一过程中每个城市可看作某个聚类中心，当蚁群从一个城市到达另一个城市时，这些聚类中心可以按照一定的规律变化。

以下是聚类过程中聚类中心选择的具体分析：

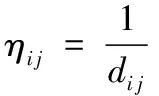
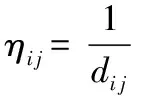
(3)数据聚类过程的分析：

当蚁群选择一个聚类中心后，这条路径中的信息素浓度会逐步的增大，这时蚁群算法中的参数Q值就会逐步变大。然而Q值越大，这样又会吸引更多的人工蚂蚁来到这个聚类中心。在本文中人工蚂蚁代表的含义需要聚类的数据，因此这些根据蚁群搜索食物的原理，相似属性的数据都能在无监督学习的条件下聚集到某个聚类中心。

当蚁群发现下一个更佳的聚类中心时，那么原来路径中人工蚁群的数量会逐步减少，并且蚁群挥发的信息素浓度也会逐步减小，此时蚁群算法的参数Q值就会逐步变小。然而在通往新聚类中心的路径上信息素浓度又会逐步增强，Q值就会逐步变大。如果Q的值越大，这样又会吸引更多的人工蚂蚁来到这个新的聚类中心，此时可以达到数据聚类的新目的。

蚁群算法在搜索食物源的过程是反复迭代的过程，因此采用蚁群算法作为聚类的过程也是一个多次迭代的过程，经过若干次反复迭代过程，需要聚类的数据都找到最好的聚类中心，最终达到数据之目的。

在3.1节的算法中对需要聚类数据进行了相似的计算，而在3.2节中采用蚁群算法为相似的数据选择了相应的聚类中心，因此经过3.1与3.2两部分算法对数据属性的计算可以完成对未知数据的聚类。

4 结束语

为了对海量数据进行相似性计算，需要采用聚类算法，聚类算法是一种智能型算法，因此在工程领域中有广泛地应用价值。本文采用数据属性的相似性计算实现了数据的聚类，而经典型的聚类算法是通过计算数据与聚类中心的距离来实现聚类的，这是不同于其他聚类算法的特征之处，蚁群算法在聚类算法中的再次应用也体现了该算法是一种寻找最优解的算法，由本文提出的聚类算法有自己的特色和不同于其它算法的地方，该算法在某种程度上具有一定的智能性，能够对某些数据进行聚类。

参考文献：

[1] 李玲娟,李 冰.一种基于特征加权的蚁群聚类新算法[J].计算技术与发展,2010,20(8):67-70.

[2] 张建华,江 贺,张宪超.蚁群聚类算法综述[J].计算机工程与应用,2006(6):171-174.

[3] 李 振,贾瑞玉.一种改进的K-means蚁群聚类算法[J].计算机技术与发展,2015,25(12):28-31.

[4] 王 鹤.蚁群聚类算法[J].中国科技信息,2007(15):280-281.

[5] 马春英,曹安得,周允征.蚁群聚类组合的改进算法[J].沈阳建筑大学学报(自然科学版).2011,27(4):798-803.

[6] 田力威,曹安得.基于信息熵的蚁群聚类组合算法的研究[J].计算机应用研究,2011,28(4):1269-1271.

[7] 向培素.聚类算法综述[J].西南民族大学学报(自然科学版),2011,37(5):112-114.

[8] 陈一昭,姜 麟.蚁群算法参数分析[J.].科学技术与工程,2011,11(36):9080-9084.

[9] 徐红梅,陈义保,刘加光,等.蚁群算法总参数设置的研究[J].山东理工大学学报(自然科学版),2008,22(1):7-11.

[10] 方 媛,车启凤.数据挖掘之聚类算法综述[J.]河西学院学报,2012,28(5):72-75.

[11] 伍育红.聚类算法综述[J].计算机科学,2015,42(6):491-524.

[12]李卫军.K-means聚类算法的研究综述[J].现代计算机，2014(8):31-36.

[13] 海 沫.大数据聚类算法综述[J].计算机科学,2016,43(6):380-383.