基于粒子群优化的图像自适应尺度空间划分方法研究
徐久成,王煜尧,董 婉
1(河南师范大学 计算机与信息工程学院,河南 新乡 453007)
2(河南省高校计算智能与数据挖掘工程技术研究中心,河南 新乡 453007)
1 引 言
近年来,人工智能在理论研究和实际应用方面都取得了很大的进展,其中,图像识别是人工智能发展进程中的重要组成部分.在图像识别的过程中,如何从原始的图像中提取有鉴别力的描述子,对于图像识别的结果起着至关重要的作用.特征匹配则是检测提取特征的一种有效的方法,其应用领域包括共同分割[1,2],图像匹配[3,4],目标探测[5,6],图像配准[7,8]等许多方面.特征匹配结果的优劣依赖于是否提取到精确的图像局部特征和健壮的特征描述.
从20世纪80年代开始,人们已经开始进行简单的图像领域研究.但是由于计算机硬件的限制,当时的图像领域研究只能采用一些特征点的对应关系做射影几何,选择一些线条作形状的分析,Harris角点探测子[9]就属于其中有关图像特征的研究成果.到了90年代末本世纪初,随着计算机硬件的革新,大批高效的图像描述子提取方法被提出,其中包括Lowe提出的SIFT特征检测和局部描述子[10],其通过收集梯度直方图来得到最终的图像描述.直至今日,仍有大批的学者[11-15]采用机器学习的方法来建立基于SIFT描述子的更加丰富的局部特征描述.
除了SIFT图像特征描述子,一些实值描述子[16-18]也相继被提出.Wang等人利用图像(块)整体的亮度顺序信息将图像块分割为若干个局部子区域,提出了用来刻画图像局部亮度顺序信息的LIOP特征描述子[17].Hauagge和Snavely提出了基于图像对称性的SYMD图像特征描述子[18],该描述子在识别具有对称性质的图像时具有很好的性能.除了这些实值描述子,许多二进制描述子[19-21]也不断被提出.其中,Rublee等人在BRISK[19]的基础上,提出了更加快速的二进制ORB描述子[20],其具有旋转不变性和抗噪的优点.另外,还有一些利用学习算法的特征提取方法,但是他们的有效性经常严重依赖训练的数据集.例如,Trzcinski等提出的BinBoost方法[22],采用一种类似AdaBoost的方法,在梯度域内使用正负patch对来训练生成的二进制描述子,在patch数据集[23]上经常优于很多方法,但是在其它的一些图像匹配数据集上它的性能就不好,相同的结论同样被许多学者所证实[15-21].基于CNN生成的特征描述子[24-26],虽然取得了很好的效果,但是却生成了将近有4000维的描述子.
最近,学者们发现,相比指定每一个特征一个探测尺度并在每一个特定的尺度上提取特征描述子的描述子提取方法[10,16,20,22],融合多个采样尺度的描述子[13-15]能够获得更加有效的特征描述.Hassner等人使用低维线性空间来近似代替一组在多尺度提取的SLS特征描述子[13].Dong等人提出了DSP-SIFT特征描述子[14],同样通过采样尺度空间,而不是在采样尺度上的描述子上执行pooling.Yang等人提出了ASV-SIFT特征描述子[15],通过不同尺度间的差异来测量特征尺度间的稳定性.然而,这些基于多个采样尺度空间的特征描述子提取方法在尺度空间的范围以及分布上依靠经验,缺少了灵活性.例如,在Hassner提出的SLS特征描述子提取方法[13]中,他们主观地在0.5到12的区间内线性等分为20个尺度;在Dong提出的DSP-SIFT特征描述子提取方法[14]中,他们主观地1/6到3/4的区间内线性等分为15个尺度;在Yang提出的ASV-SIFT特征描述子提取方法[15]中,他们主观地1/6到3的区间内线性等分为若干个尺度.因此,本文提出一种自适应的尺度空间划分方法(PSO-ASV),采用基本的粒子群算法,自适应地找寻到最佳的尺度划分方案.
2 相关工作
2.1 SIFT 描述子
尺度不变特征转换(Scale-Invariant Feature Transform,SIFT)[10]是一种有效的用来探测与描述图像中局部特征的算法,其在空间尺度中寻找极值点,然后提取出相关的位置、尺度和旋转不变量.SIFT图像特征描述子的提取主要分为两步:特征点的探测和描述子的生成.
图像I(x,y)通过与实现尺度变换的高斯函数G(x,y,σ)[27]的卷积运算,进而构建尺度空间L(x,y,σ) :
L(x,y,σ)=G(x,y,σ)*I(x,y)
(1)
其中,高斯函数G(x,y,σ)为:
(2)
在尺度空间采用高斯差分(DoG)函数探测到方向和尺度不变特性的特征点.通过对比度去除一些对比度较低的特征点,另外还去除一些不稳定的边缘响应点.计算出探测到的特征点与其附近像素间的梯度方向分布特性,选取梯度值最大的方向为当前特征点的方向,使得提取的局部描述子具有旋转不变的特性.采用梯度直方图的方式,每一个特征点最终生成了一个128维的特征描述向量.梯度的计算如下:
m(x,y)=
(3)
θ(x,y)= tan-1((L(x,y+1)-L(x,y-1))/
(L(x+1,y)-L(x-1,y)))
(4)
其中,m(x,y)和θ(x,y)分别为在特征点(x,y)处梯度的模值和方向.
2.2 累积稳定性投票
累积稳定性投票(Accumulated stability voting,ASV)与SLS[13],DSP-SIFT[14]类似,都是在多尺度空间上提取特征描述子.首先,在被探测尺度σ的近邻尺度(λsσ,λlσ)范围内线性等分地采样ns个尺度.其中,λs表示最小尺度的缩放比例;λl表示最大尺度的缩放比例.
然后在每一个采样的尺度的同一个特征点上提取一个SIFT描述子,并求出在两个不同的尺度采样的SIFT描述子的差的绝对值vi,j.vi,j用来度量尺度i和尺度j之间的每一个特征点之间的稳定性,表示为:
vi,j=xi-xj
(5)
其中,xi和xj是从i和j(1≤i,j≤ns)两个不同的尺度提取的SIFT描述子,运算符 | · | 表示输入向量的每一个元素的绝对值.由于在每一个尺度上的每一个特征点都对应一个128维的SIFT描述子,因此,尺度之间的稳定性可以另表示为:
(6)

hm=θt(vm|tm)
(7)
其中,θt为阈值函数,tm为选定的阈值.最后,对所有尺度对所得的二进制形式的稳定性hm执行pooling,得到度量稳定性的实值描述子C:
(8)
最终得到的描述子C即为ASV-SIFT.
3 基于PSO的自适应尺度划分的描述子生成
近年来,实验表明融合多个采样尺度的描述子[13-15]能够获得更加有效的特征描述.尺度的划分在此类方法中起到至关重要的作用,然而,如何进行尺度的划分却没有一个准确的方法.在基于尺度空间的特征描述方法中,都采用主观的经验来进行较为合理的尺度划分,并没有一种高效的尺度划分方法.因此,我们提取了一种基于粒子群算法[27]的自适应尺度划分方法,并将其应用于ASV描述子提取方法中,最终得到高效的描述子提取方法(AD-ASV).
在基于多个采样尺度的描述提取算法中,λs和λl分别表示最小尺度和最大尺度的缩放比例,两者的取值直接影响着最终提取的描述子能否有准确的图像描述,采用粒子群优化算法,来自适应地寻找到能够准确描述图像信息时λs和λl的值.
首先,随机选取范围为1到10的值作为λs和λl的初始值,同时作为粒子群算法的初始值.采用初始的λs和λl值作为初始的尺度划分方式,通过ASV-SIFT方法计算出当下的适应值,然后对第i个粒子的速度和位置进行更新,更新方式如下:
vid=vid+c1r1(pid-xid)+c2r2(pgd-xgd)
(9)
xid=xid+vid
(10)
其中,vid和xid分别为粒子的速度和位置,pid和pgd分别是第i个粒子和整个粒子群迄今为止搜索到的最优位置,c1和c2是非负的学习因子,r1和r2是介于0和1之间的随机数.
迭代中止条件根据粒子群当前搜索到的最优位置是否大于同等设置下的ASV的最优值.如果大于采用ASV得到的值,则终止迭代并返回当前搜索到的最优位置对应的λs和λl的值.完整的算法流程见算法1.
算法1. 基于PSO的自适应尺度划分的描述子生成算法.
输入:群体规模m,加速常数c1和c2,最大代数Gm
输出:适应值mAP,最小尺度的缩放比例λs和最大尺度的缩放比例λl
Step1. 初始化一群群体规模为m的粒子,包括每个粒子初始位置xid和速度vid;
Step2. 采用ASV描述子提取方法,计算每个粒子的适应值mAP,即图像特征点的匹配准确率;
Step3. 对每个粒子,如果它的适应值mAP大于它经历过的最好位置pbest的适应值mAPpb,则将其作为当前的最好位置pbest并将其适应值更新为mAPpb;
Step4. 对每个粒子,如果它的适应值mAP大于全局所经历最好位置gbest的适应值mAPgb,则将其作为当前全局的最好位置gbest并将其适应值更新为mAPgb;
Step5. 根据公式(9)和公式(10)来更新粒子的速度和位置;
Step6. 如未找到一个优于在相同条件下ASV达到的mAP或未达到预设最大代数Gm,返回Step2;反之,则输出当前的适应值mAP以及相应的λs和λl;
Step7. 算法结束.
4 实验与结果
4.1 数据集
本文将在Oxford[28]和Fischer[24]两个图像匹配数据集上进行实验来验证所提算法的有效性.Oxford数据集包含模糊、压缩、视角变化和光照等变换的40个图像对;Fischer数据集弥补了Oxford数据集变换类型不足的缺陷,提供了包含模糊、缩放、旋转、视角变化和非线性变换等变换更加多样的400个图像对.
4.2 实验设置与分析
所有的实验将在Ubuntu 12.04上进行,采用Matlab R2012a编程软件.采用VLFeat工具箱[29]提取经典的描述子,例如SIFT描述子,LIOP描述子等.采用Mikolajczyk和Schmid的结果评价方法[30],计算各个算法的匹配和实际匹配的交除并值(intersection-over-union,IoU),如果超过50%,就认定该匹配是正确的.相比其它基于尺度空间的描述子提取方法,ASV方法由于获得了更好的匹配结果,因此,本文提出的自适应尺度划分方法将应用在ASV描述子提取方法上.
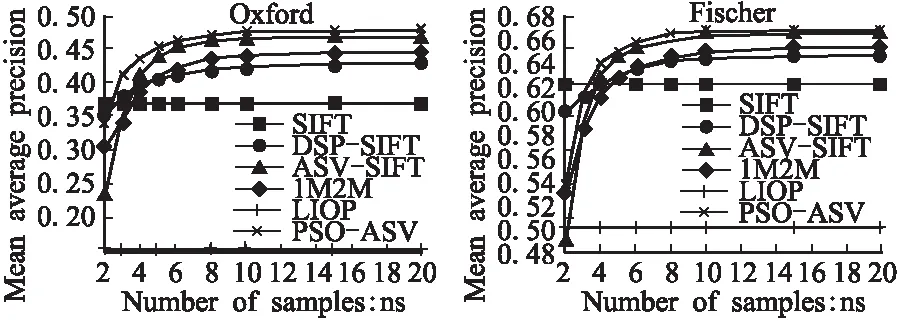
图1 不同的描述子对应的平均准确率Fig. 1 Mean average precision of different descriptors
在不同的尺度划分数目上比较本文所提PSO-ASV方法与多种相关方法的平均匹配准确率mAP.在Oxford数据集和Fischer数据集上的实验结果如图1所示.
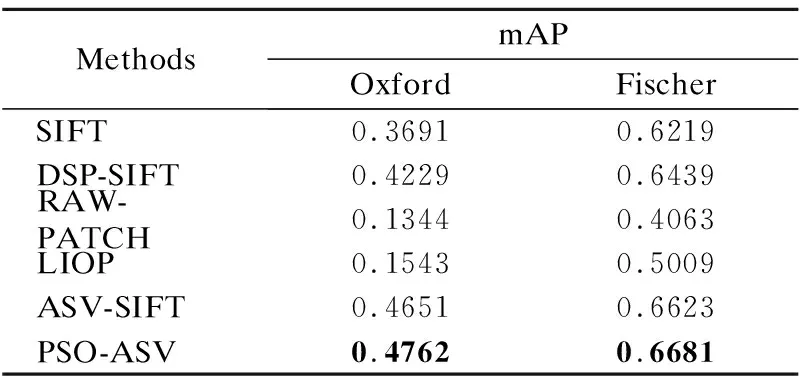
表1 不同描述子的平均准确率比较Table 1 Comparison of mean average precision of different descriptors
从表1中可以看出,当尺度空间的划分数目达到10时,本文所提的PSO-ASV方法都优于其它方法.其中,SIFT,RAW-PATCH,LIOP都不是基于尺度空间的特征描述子,DSP-SIFT,ASV-SIFT是基于尺度空间的特征描述子.为了能够进一步验证本文所提方法的有效性,本文在Oxford数据集上又做了一些对比实验,在每个类型的图像对中选择变换最大的图像对来绘制出P-R曲线来评价文中所提方法,实验结果如图2所示.
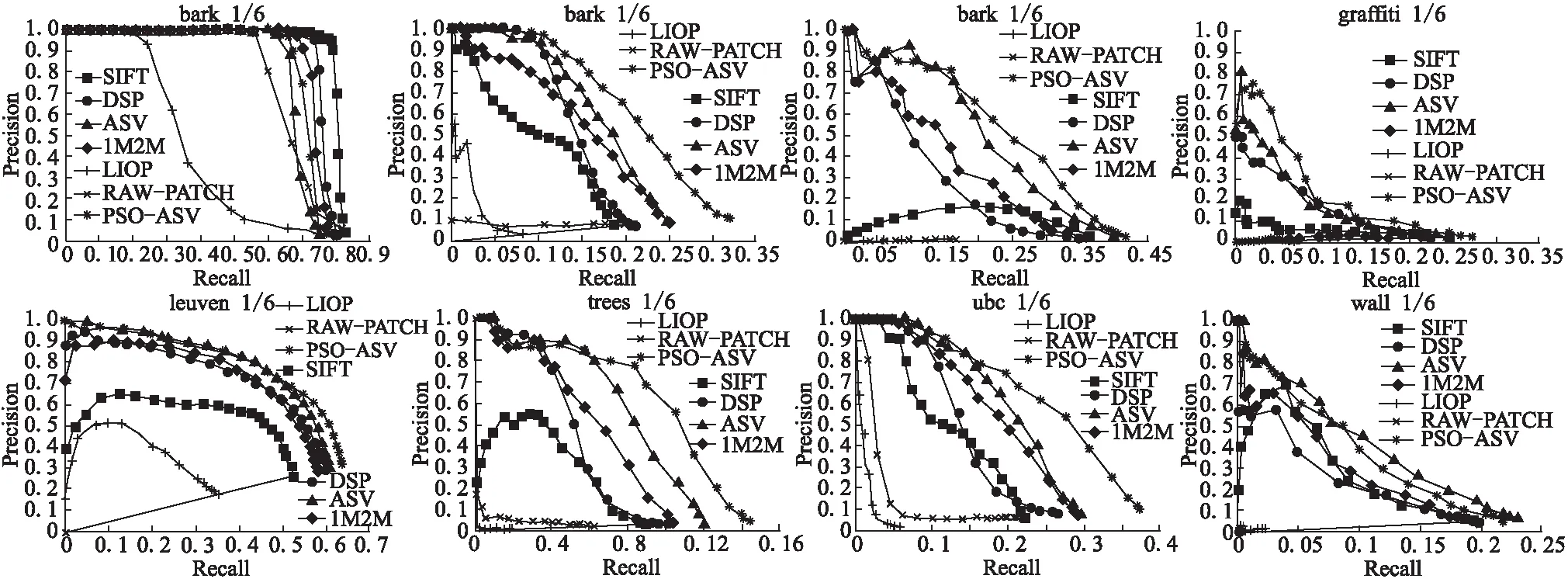
图2 Oxford数据集的8个变换最大的图像对的P-R曲线Fig. 2 P-R curves of eight extreme pairs in the Oxford dataset
从图2可以看出,在多种图像变换方式中,相比其它方法,PSO-ASV方法大都取得了较好的结果,只是在对于视角的变换的wall图像对匹配中,效果不明显.除此之外,本文分析了在不同的图像变化强度下采用不同的特征描述子实现的特征点正确匹配数目,实验结果如图3所示.图3实验结果表明,PSO-ASV方法能够在模糊、压缩和光照变化等图像变换中获得很好的匹配结果,但是对于视角的变换,效果不明显.

图3 在Oxford数据集上,不同的描述子在不同的变换强度下的正确特征点匹配数量Fig. 3 Number of correct correspondences using different descriptors under different transformation magnitudes in the Oxford dataset
在图4中,选取其它的基于尺度空间的描述子提取方法与PSO-ASV方法作head-to-head比较,画布中的每一个点代表使用选择的两个特征描述子匹配的其中一个图像对的平均准确率.从图4中看到,相比SIFT、DSP-SIFT、ASV-SIFT和1M2M,PSO-ASV能够取得更好的匹配结果,也说明本文方法获取了更加精确的图像描述.

图4 PSO-SIFT分别与其它相关方法的head-to-head比较Fig. 4 Head-to-head comparisons between PSO-SIFT and other relative methods
5 总 结
本文提出了新的图像尺度空间划分方法,通过引入粒子群算法,根据描述子的提取方式及尺度空间划分的数目自适应地划分尺度空间.实验结果表明,PSO-ASV方法能够在任何尺度划分数目和特征提取方法下,找到更优的图像尺度划分.虽然PSO-ASV提高了特征匹配的准确率,但是却不可避免地增加了时间的消耗,因此,如何能够更加高效地自适应找寻更优的图像尺度划分,是我们下一步研究的方向.
:
[1] Rubio J,Serrat J,López A,et al.Unsupervised co-segmentation through region matching [C] .Proc of the 25th IEEE Conference on Computer Vision and Pattern Recognition(CVPR),Piscataway,NJ:IEEE,2012:749-756.
[2] Chen H,Lin Y,Chen B.Co-segmentation guided hough transform for robust feature matching [J].IEEE Transactions on Pattern Analysis and Machine Intelligence(TPAMI),2015,37(12):2388-2401.
[3] Chen H,Lin Y,Chen B.Robust feature matching with alternate hough and inverted hough transforms [C] .Proc of the 26th IEEE Conference on Computer Vision and Pattern Recognition(CVPR),Piscataway,NJ:IEEE,2013:2762-2769.
[4] Yang T,Lin Y,Chuang Y.Accumulated stability voting:a robust descriptor from descriptors of multiple scales [C].Proc of the 29th IEEE Conference on Computer Vision and Pattern Recognition(CVPR),Piscataway,NJ:IEEE,2016:327-335.
[5] Dalal N,Triggs B.Histograms of oriented gradients for human detection [C].Proc of the 18th IEEE Conference on Computer Vision and Pattern Recognition(CVPR),Piscataway,NJ:IEEE,2005,1:886-893.
[6] Felzenszwalb P,Girshick R,McAllester D,et al.Object detection with discriminatively trained part-based models [J].IEEE Transactions on Pattern Analysis and Machine Intelligence(TPAMI),2010,32(9):1627-1645.
[7] Liu C,Yuen J,Torralba A.SIFT flow:dense correspondence across scenes and its applications [J].IEEE Transactions on Pattern Analysis and Machine Intelligence(TPAMI),2011,33(5):978-994.
[8] Hsu K,Lin Y,Chuang Y.Robust image alignment with multiple feature descriptors and matching-guided neighborhoods [C].Proc of the 28th IEEE Conference on Computer Vision and Pattern Recognition(CVPR),Piscataway,NJ:IEEE,2015:1921-1930.
[9] Harris C,Stephens M.A combined corner and edge detector [C] .Proc of the 4th Alvey Vision Conference,Citeseer,1988:147-151.
[10] Lowe D.Distinctive image features from scale-invariant keypoints [J].International Journal of Computer Vision(IJCV),2004,60(2):91-110.
[11] Lazebnik S,Schmid C,Ponce J.Beyond bags of features:spatial pyramid matching for recognizing natural scene categories [C].Proc of the 19th IEEE Conference on Computer Vision and Pattern Recognition(CVPR),Piscataway,NJ:IEEE,2006,2:2169-2178.
[12] Yang J,Yu K,Gong Y,et al.Linear spatial pyramid matching using sparse coding for image classification [C].Proc of the 22th IEEE Conference on Computer Vision and Pattern Recognition(CVPR),Piscataway,NJ:IEEE,2009:1794-1801.
[13] Hassner T,Mayzels V,Zelnik-Manor L.On sifts and their scales [C].Proc of the 25th IEEE Conference on Computer Vision and Pattern Recognition(CVPR),Piscataway,NJ:IEEE,2012:1522-1528.
[14] Dong J,Soatto S.Domain-size pooling in local descriptors:DSP-SIFT [C].Proc of the 28th IEEE Conference on Computer Vision and Pattern Recognition(CVPR),Piscataway,NJ:IEEE,2015:5097-5106.
[15] Yang T,Lin Y,Chuang Y.Accumulated stability voting:a robust descriptor from descriptors of multiple scales [C] .Proc of the 29th IEEE Conference on Computer Vision and Pattern Recognition(CVPR),Piscataway,NJ:IEEE,2016:327-335.
[16] Tola E,Lepetit V,Fua P.DAISY:an efficient dense descriptor applied to wide-baseline stereo [J].IEEE Transactions on Pattern Analysis and Machine Intelligence(TPAMI),2010,32(5):815-830.
[17] Wang Z,Fan B,Wu F.Local intensity order pattern for feature description [C] .Proc of the 13th International Conference on Computer Vision(CVPR),Piscataway,NJ:IEEE,2011:603-610.
[18] Hauagge D,Snavely N.Image matching using local symmetry features [C].Proc of the 25th IEEE Conference on Computer Vision and Pattern Recognition(CVPR),Piscataway,NJ:IEEE,2012:206-213.
[19] Leutenegger S,Chli M,Siegwart R.BRISK:Binary robust invariant scalable keypoints [C].Proc of the 24th IEEE Conference on Computer Vision and Pattern Recognition(CVPR),Piscataway,NJ:IEEE,2011:2548-2555.
[20] Rublee E,Rabaud V,Konolige K,et al.ORB:An efficient alternative to SIFT or SURF [C] .Proc of the 13th International Conference on Computer Vision(CVPR),Piscataway,NJ:IEEE,2011:2564-2571.
[21] Balntas V,Tang L,Mikolajczyk K.BOLD-binary online learned descriptor for efficient image matching [C].Proc of the 28th IEEE Conference on Computer Vision and Pattern Recognition(CVPR),Piscataway,NJ:IEEE,2015:2367-2375.
[22] Trzcinski T,Christoudias M,Fua P,et al.Boosting binary keypoint descriptors [C].Proc of the 26th IEEE Conference on Computer Vision and Pattern Recognition(CVPR),Piscataway,NJ:IEEE,2013:2874-2881.
[23] Brown M,Hua G,Winder S.Discriminative learning of local image descriptors[J].IEEE Transactions on Pattern Analysis and Machine Intelligence(TPAMI),2011,33(1):43-57.
[24] Fischer P,Dosovitskiy A,Brox T.Descriptor matching with convolutional neural networks:a comparison to sift [J].ArXiv Preprint ArXiv:1405.5769,2014
[25] Han Xu-feng,Leung T,Jia Yang-qing,et al.MatchNet:unifying feature and metric learning for patch-based matching [C] .Proc of the 28th IEEE Conference on Computer Vision and Pattern Recognition(CVPR),Piscataway,NJ:IEEE,2015:3279-3286.
[26] Zagoruyko S,Komodakis N.Learning to compare image patches via convolutional neural networks[C].Proc of the 28th IEEE Conference on Computer Vision and Pattern Recognition(CVPR),Piscataway,NJ:IEEE,2015:4353-4361.
[27] Kennedy J,Eberhart R.Particle swarm optimization [C] .Proc of the IEEE International Conference on Neural Networks,Perth,Australia,1995:1942-1948.
[28] Hua G,Brown M,Winder S.Discriminant embedding for local image descriptors [C].Proc of the11th IEEE International Conference on Computer Vision(ICCV),Piscataway,NJ:IEEE,2007:1-8.
[29] Vedaldi A,Fulkerson B.VLFeat-an open and portable library of computer vision algorithms [C].Proc of the 18th ACM International Conference on Multimedia,New York:ACM,2010:1469-1472.
[30] Mikolajczyk K,Schmid C.A performance evaluation of local descriptors [J].IEEE Transactions on Pattern Analysis and Machine Intelligence(TPAMI),2005,27(10):1615-1630.

