邻域粗糙集模型的规则提取方法研究

姚 晟，徐 风，赵 鹏，汪 杰，陈 菊

1(安徽大学 计算机科学与技术学院，合肥 230601)

2(安徽大学 计算智能与信号处理教育部重点实验室，合肥 230601)

1 前 言

粗糙集理论[1]是波兰学者Z.Pawlak 于1982年提出的一种新的处理模糊和不确定性知识的数学模型，其主要方法是通过上近似和下近似去刻画不确定信息[2,3]，并且通过属性约简[4]消除冗余属性，简化数据结构，导出问题和分类的规则[5].目前，粗糙集理论已被成功地应用于机器学习[6]、神经网络[7]、模式识别[8]和数据挖掘[9]等领域.经典粗糙集模型建立在等价关系的基础上，只能处理符号型属性，而在现实的很多信息系统中存在大量的数值型属性，这使得经典粗糙集理论的运用具有一定的局限性.为了能让经典粗糙集模型能在数值型数据上有着很好的运用，目前常用的方法是将数值型属性经过离散化处理[10]，使其转化成符号型属性，但是这样处理又会丢失数据中很多信息，因此数据离散化处理并不是一种很好的解决办法.为了较好地解决此类问题，Lin等[11-13]利用距离去定义对象之间的相似性，提出邻域关系代替等价关系，将经典粗糙集模型推广为邻域粗糙集模型.邻域粗糙集模型最大的优势在于可以直接处理数值型属性的数据，因此比起经典粗糙集模型，邻域粗糙集模型有着更加广泛的适用范围.

包含数值型属性的信息系统被称为邻域信息系统[11].在邻域信息系统中，由邻域关系导出的邻域类中对象间属性值均不完全相同，这给信息系统的规则提取带来很大麻烦，因此无法导出一个明确的决策规则.并且对于一个所给的规则前件，如果各属性值与已知的信息系统的取值匹配不完全一致，则无法判定它的决策值.所以邻域信息系统中的规则提取是一个很大的难题.

近年来，Zhu等[14]提出在邻域信息系统中存在着大量的冗余对象，并指出信息系统中少部分对象就可以表达整个全域的信息，因此可以将这些少部分对象作为整个信息系统的决策规则，但是文中并未给出规则提取全面系统化的方法.本文在此基础上，针对邻域粗糙集模型中规则提取的问题，定义一种特殊的决策规则形式，给出规则诱导的方法，并且对于待决策的规则前件，给出其决策的判定方法.最后通过UCI数据集实验验证了本文所提方法在邻域粗糙集规则提取方面具有一定的可行性和合理性.

2 基本理论

2.1 经典粗糙集模型

定义1.称IS=(U，A，V，f)为信息系统，其中U为有限对象集合，A为属性集，V为属性的值域，f为属性到属性值域上的映射，即f(x，a)=v表示对象x在属性a下的取值为v，可简单表示为a(x)=v.

对于∀B⊆A，记

RB={(x，y)ak(x)=ak(y)，∀ak∈B}，

(1)

则RB是U上的等价关系，对象x的等价类定义为[x]B={y(x，y)∈RB}.因此由等价关系RB在U上产生的划分为U/RB={[x]Bx∈U}.

定义2.对于∀X⊆U，设

(2)

(3)

(4)

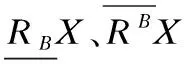
称DIS=(U，A=C∪D，V，f)为决策信息系统，其中属性集A由条件属性集C和决策属性集D组成.在决策信息系统中，决策规则是由一系列属性和属性值构成的基本单元组成[15]，可表示为∧(a，va)→∨(d，vd)，其中a∈C，d∈D，v∈V.若设φ=∧(a，va)，φ=∨(d，vd)，则决策规则也可简单表示为：

φ→φ，

其中φ称为决策规则的前件，φ称为决策规则的后件，即根据前件所作出的决策.

定义3.对于决策信息系统DIS=(U，A=C∪D，V，f)，设决策属性划分为U/RD={D1，D2，…，Dm}，Dec(X)为对象集X的描述，则该决策信息系统导出的决策为Di的确定性规则可表示为[16]：

(5)

从定义3可以看出，决策类的下近似集中对象所描述的决策规则即为该决策的确定性规则.

2.2 邻域粗糙集模型

定义4.设对象xi∈U且B⊆C为数值型属性，则xi在B上的邻域δB(xi)定义为[11]

δB(xi)={xjxj∈U，ΔB(xi，xj)≤δ}，

(6)

其中Δ为距离函数，δ为邻域半径.

从定义4可以看出，对象的邻域大小由Δ距离函数和邻域半径共同决定.目前Δ距离函数广泛采用的是闵可夫斯基(Minkowski)距离[17]，对象xi，xj间的闵可夫斯基距离定义为

(7)

其中A={a1，a2，…，an}.

此外，闵可夫斯基距离有三种常用的特殊形式，分别为当p取值为1、2和∞时的情形.当p=1时，即

(8)

此距离又称为绝对值距离；

当p=2时，即

(9)

此距离又称为欧氏距离；

当p=∞时，即

(10)

此距离又称为切比雪夫距离.

定义5.设邻域决策信息系统为NDIS=(U，A=C∪D，f)，C，D分别为条件属性和决策属性，对于∀X⊆U在邻域关系B⊆C的下近似集和上近似集以及边界域分别定义为[11]

(11)

(12)

(13)

从定义5可以看出，当邻域半径选取为0时，邻域粗糙集模型就转化为经典粗糙集模型.

3 邻域粗糙集模型规则提取与判别

3.1 邻域粗糙集模型的规则提取

由于邻域粗糙集模型中属性的类型为数值型，无法运用属性与属性值的形式去描述决策规则，因此本文定义了一种新的决策规则形式来描述邻域决策系统中的规则.

定义6.对于邻域决策信息系统NDIS=(U，A=C∪D，V，f)，C为条件属性集且均为数值型属性，D为决策属性集.定义邻域决策信息系统中导出决策规则形式为：

Φ→d.

(14)

其中，Φ⊆U为对象子集，称为决策规则的前件，d为决策值，称为决策规则的后件.

定义6中定义的决策规则是通过一个对象集的整体作出相应决策的形式来描述，这种表达方式相对于经典粗糙集模型中的形式显得较为复杂，但是由于数值型属性的取值为数值，存在大量相近的数据，采用传统方法导出规则将会产生大量冗余，因此这样定义的形式相比较具有一定的合理性.

对于决策信息系统中确定性规则的提取，经典粗糙集理论通过对决策类求取下近似的方法来得到[3]，即通过下近似对象集描述的决策规则为确定性规则.同样地，本文也运用类似方法来导出邻域决策信息系统的确定性决策规则.

定义7.在邻域决策信息系统NDIS=(U，A=C∪D，V，f)中，决策属性值域VD={d1，d2，…，dm}，其对应决策类为D1，D2，…，Dm，则信息系统中蕴含的确定性决策规则为：

(15)

如果我们将决策规则前件中集合的基数大小称为决策规则的规模，从定义7中可以看出，决策规则前件是由决策类基于条件属性的下近似集构成的，那么下近似集的大小将直接决定决策规则的规模.而在邻域粗糙集模型中，选取相同的距离函数，邻域半径的大小将直接影响到下近似集的大小，结合定义4和定义5可以得到，随着邻域半径的增大，近似对象的下近似集将随之减小[18].因此在导出决策规则中，选取过于小的邻域半径使得下近似集过大，则这样得到的决策规则的规模就很大，而邻域半径选取过大虽然能使决策规则的规模变小，但是过小导出的决策规则在决策的精确度方面就可能会很低，因此我们需要选取一个合适的邻域半径，使得决策规则的规模较小且决策的精确度较高.我们称这个邻域半径为最优邻域半径，选取最优邻域半径导出的决策规则称为最优的决策规则.

3.2 邻域粗糙集模型的决策判定

由于本文定义的决策规则前件是由对象集表示的，并没有给出对应属性具体的取值，因此对于一个待决策的规则前件，一般情况下很难直接判断出它的决策.为了解决此类问题，本文这里给出一个通过距离判别的方法来对规则决策进行判定.

Δ(X，G)=(X-μ)Ω(X-μ)T.

(16)

马哈拉诺比斯距离简称马氏距离，是描述一个n维向量与一组m个n维向量距离远近的公式，因此我们可以将这个公式引入到邻域粗糙集模型中，将邻域信息系统中每个对象在条件属性下取值的序列看成一个向量，然后根据马氏距离可以得到一个对象与一个对象集之间的距离.

(17)

从定义9可以看出，对于一个待决策的规则前件，其决策值取决于所给前件与已知规则前件距离的远近，最终的决策选取为规则前件最近的决策值.在经典粗糙集模型诱导的决策中，当决策规则前件相同时，对应的决策值是相同的[15-16]，这就相当于本文这里距离为0时的情形，因而本文所提出的决策判别方法为传统方法的推广.

4 实验分析

为了验证本文所提出的方法具有一定可行性和合理性，本实验从UCI 机器学习数据库获取了7个数据集进行实验分析和评估.经过整理后数据集描述如表1所述：

表1 UCI数据集Table 1 UCI data sets

本文实验环节主要分为两部分，第一部分为验证性实验，即对表1中的每个数据集随机选取三分之二作为训练集进行规则提取，然后再将剩余的三分之一作为测试集对这些规则进行测试，通过测试集决策的精确度来验证本文提出方法的可行性.第二部分实验主要探究随着邻域半径变化，决策规则的精确度和决策规则的规模的变化，并给出最优邻域半径的选取问题.

为了消除数据集属性量纲的影响，在进行实验前所有数据集都经过了标准化处理，本实验选用是极差标准化变换[17]，并且距离函数选取为欧氏距离.根据定义4可以看出，邻域半径的选取和数据集属性的个数有着很直接的关系，这对最优邻域半径的统一带来了不便，为了解决这一问题，本实验采用文献[14，18]中关于邻域半径的表示，即：

δ=min(Δ)+w·[max(Δ)-min(Δ)]

(18)

其中min(Δ)，max(Δ)分别表示数据集中所有对象之间距离的最小值和最大值，w为比例系数，满足0≤w≤1.当w=0时，δ=min(Δ)，当w=1时，δ=max(Δ)，这样就可以通过w的选取来决定邻域半径的大小.

图1展示的是各个数据集在第一部分实验的结果.在不同w取值下，通过训练集诱导出决策规则，然后对测试集中每个对象进行决策判别，并与真实决策进行比对，我们将测试集中决策正确的对象数目与总测试数目的比值作为对应w值下决策规则的精确度，为了避免偶然性，我们将实验反复进行7次.图中每条曲线代表每次的实验结果.

观察图1可以发现，测试集决策规则的精确度在w值的[0，0.2]区间上能够达到较高的水平，由于决策规则的精确度反映了决策规则整体对决策判别的正确率，所以运用本文方法导出的决策规则来进行决策判别，其决策结果具有较高的精确度，说明在邻域决策信息系统的规则提取中，这种决策规则形式是可行的.由于邻域决策信息系统中的属性值是连续的，传统的方法很难进行规则提取，因而本文的这种形式的规则不失为一种有效的方法.

由于实验的第一部分验证了方法的可行性，那么实验的第二部分将对每个数据集进行规则提取，并计算其精确度和决策规则的规模，具体结果如图2所示.这里的精确度为训练集和测试集均为整个数据集的计算结果，数据集决策规则规模为每个规则的规模之和.

观察图2可以发现，随着w值的逐渐增大，即邻域半径的逐渐增大，其邻域决策信息系统的决策规则精确度一开始稳定在较高的值，然后逐渐减小至0，说明对于w值选取不宜过大，通过这7个数据集的实验结果可以发现，w取值在[0，0.2]区间内决策规则精确度几乎达到最高，因此在本文提出的规则提取方法中，对于邻域半径的选取，其w值应取[0，0.2]为宜.同时，对于图2中展示的实验结果，随着w值的逐渐增大，决策规则的规模是逐渐减小的，规模的减小意味着决策规则前件所包含的对象越少.由于在定义8所示的规则判定中，需要进行矩阵运算，因而更小规模的规则具有更高的判别效率.因此综合规则精确度和规则的规模，我们需要选取一个精确度又高且规模又小的w值，这个w值正是我们要找的最优邻域半径对应w值，可以看出，本实验得出的最优邻域半径对应的w值为0.2.

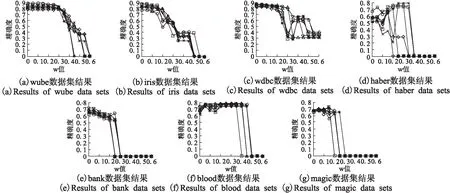
图1 各数据集第一部分实验结果Fig.1 Experimental results of the first part of each data set

图2 各数据集第二部分实验结果Fig.2 Experimental results of the second part of each data set

表2 wdbc数据集部分结果Table 2 Partial results on wdbc data sets

但是，在实际的需求中，有时往往可能需要尽可能缩小决策规则的规模，以达到进一步简化决策规则的效果.或者是追求高精确度的情形，这时我们可以根据要求灵活的选取w值的大小.表2和表3所示的是数据集wdbc和magic在不同的w值下决策规则规模和规则精确度结果.表中的规模值为数据集每个决策规则的规模值之和.

从表2-3可以看出，对于尽量缩小规模，数据集wdbc的w值可以选择0.25，数据集magic可以选择0.2，这样使得决策精确度不会太低且大幅度减少了规则前件中对象的数量，从而提高了决策判别效率.

通过本实验，证明了本文所提出的决策规则形式具有一定的可行性和合理性，应用于邻域决策信息系统的决策提取是合适的.并且通过实验给出了规则提取中邻域半径的选取范围以及最优邻域半径的取值，这个取值具有一定的通用性，可以为实际应用提供参考.

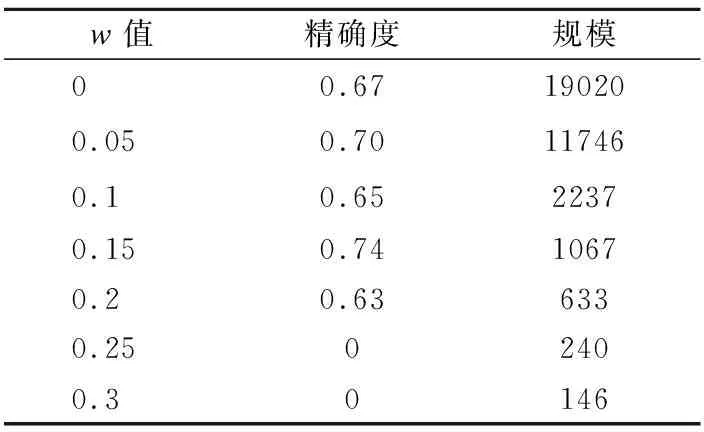
表3 magic数据集部分结果Table 3 Partial results on magic data sets

5 结 语

本文针对目前邻域粗糙集模型中关于规则提取的问题，提出一种特殊形式的决策规则，该决策规则利用对象集作为规则的前件，并给出规则的诱导方法，并且对于待决策的规则前件，通过对已知规则的前件进行距离判别，然后得到对应的决策.UCI数据集的实验结果表明，导出的决策规则对于决策的判别具有较高的准确性，并且决策规则的规模程度也比较小.因此可以看出，本文提出的决策规则提取方法具有一定的可行性和合理性.在接下来的工作中需要进一步探究混合数据类型信息系统的决策规则诱导方法.

：

[1] Pawlak Z.Rough sets[J].International Journal of Computer and Information Sciences，1982，11(5)： 341-356.

[2] Jia Xiu-yin，Shang Lin，Zhou Bing，et al.Generalized attribute reduct in rough set theory[J].Knowledge-Based Systems，2016，91：204-218.

[3] Zhang Wen-xiu，Wu Wei-zhi，Liang Ji-ye，et al.Rough set theory and method[M].Beijing：Science Press，2001.

[4] Teng Shu-hua，Lu Min，Yang A-feng.Efficient attribute reduction from the viewpoint of discernibility[J].Information Sciences，2016，326(C)：297-314.

[5] Huo Lei，Wang Zhi-liang，Automation S O.Rough set based rules extraction method for smart home[J].Modern Electronics Technique，2016.

[6] Shen Kao-yi，Tzeng G H.Contextual improvement planning by fuzzy-rough machine learning： a novel bipolar approach for business analytics[J].International Journal of Fuzzy Systems，2016,18(6):1-16.

[7] Salama M A，Hassanien A E，Mostafa A.The prediction of virus mutation using neural networks and rough set techniques[J].Eurasip Journal on Bioinformatics & Systems Biology，2016，2016(1)：1-11.

[8] Shao Y E，Chiu C C.Applying emerging soft computing approaches to control chart pattern recognition for an SPC-EPC process[J].Neuro Computing，2016，201(92)：19-28.

[9] Chen Li-fen，Tsai C T.Data mining framework based on rough set theory to improve location selection decisions： A case study of a restaurant chain[J].Tourism Management，2016，53：197-206.

[10] Bermanis A，Salhov M，Wolf G.Measure-based diffusion grid construction and high-dimensional data discretization[J].Applied & Computational Harmonic Analysis，2015，40(2)：207-228.

[11] Lin T Y，Neighborhood systems and approximation in database and knowledge base systems[C].Proceedings of the Fourth International Symposium on Methodologies of Intelligent Systems，Poster Session，1989：75-86.

[12] Lin T Y.Granular and nearest neighborhoods： rough set approach[J].Studies in Fuzziness & Soft Computing,2001,70(15)：125-142.

[13] Lin T Y.Granular computing on binary relations I：data mining and neighourhood systems[C].Rough Sets in Knowledge Discovery，1998：107-121.

[14] Zhu Peng-fei，Hu Qing-hua.Rule extraction from support vector machines based on consistent region covering reduction[J].Knowledge-Based Systems，2013，42(2)：1-8.

[15] Wang Yong-sheng，Zheng Xue-feng，Suo Yan-feng.A dynamic rule extraction based on information granularity model for complete data[C].IEEE International Conference on Granular Computing，IEEE,2014：329-333.

[16] She Yan-hong，Li Jin-hai，Yang Hai-long.A local approach to rule induction in multi-scale decision tables[J].Knowledge-Based Systems，2015，89(C)：398-410.

[17] Gao Hui-xuan.Applied multivariate statistical analysis[M].Beijing：Beijing University Press，2005：218-228.

[18] Hu Qing-hua，Yu Da-ren，Xie Zong-xia.Neighborhood classifiers[J].Expert Systems with Applications An International Journal，2008，34(2)：866-876.

[19] Brereton R G ，Lloyd G R.Re-evaluating the role of the Mahalanobis distance measure[J].Journal of Chemometrics，2016，30(4)：134-143.

附中文参考文献：

[3] 张文修，吴伟志，梁吉业，等.粗糙集理论与方法[M].北京：科学出版社，2001.

[17] 高惠璇.应用多元统计分析[M].北京：北京大学出版社，2005.