自适应参数调整的近邻传播聚类算法

王卫涛,钱雪忠,曹文彬

1(江南大学 物联网工程学院 智能系统与网络计算研究所,江苏 无锡 214122)

2(物联网技术应用教育部工程研究中心,江苏 无锡 214122)

3(江南大学 物联网工程学院,江苏 无锡 214122)

1 引 言

聚类分析是对一组数据对象或者物理对象进行处理,最终将对象分成几类,使得同一类对象之间的相似度更大,不同类对象之间的相似度更小.聚类分析已经应用在了数据挖掘,图像压缩,图像边缘检测,基因识别,面部识别和文档检索等领域.在聚类分析的发展过程中,相继提出了k-means,DBSCAN,FCM等一系列的聚类算法,近邻传播算法作为一个新型的聚类算法,2007年Frey和Dueck在Science上发表了Points Clustering by Passing Messages Between Data,系统阐述了近邻传播聚类算(Affinity Propagation,AP)的原理和应用.与其他聚类方法相比,近邻传播算法不需要事先设定聚类的个数,不需要初始化聚类中心点,是一种快速有效的聚类算法,但是在研究的过程中,发现近邻传播算法的偏向参数和聚类个数对最终聚类结果的准确性影响很大.当偏向参数越大时,最终的聚类个数就会越多,偏向参数越小,最终聚类的个数就会越少.传统AP算法选择相似度矩阵的均值作为偏向参数,对于任意分布的数据集,相似度矩阵的均值并不是最好的选择;同时该算法聚类的类数与实际类数有差异,如何使得聚类个数更接近真实类数,同时不影响聚类准确性,这也是一个需要讨论的热点.

针对上述问题,Kaijun Wang[1]提出了自适应近邻传播聚类(AAP),该方法基于梯度下降自适应的选择偏向参数,然而当以固定步长扫描p的空间时,无法精确的获得全局最优解;Xian-hui Wang[2]提出了基于粒子群智能算法自适应搜索最佳的偏向参数(PAAP);B.Jia[3]提出了基于布谷鸟智能算法自适应搜索最佳的偏向参数(CAAP);Libin Jiao[4]提出了基于黄金分割和遗传算法自适应搜索最佳的偏向参数(GS-AP,GA-AP).文献[2,3,4]中提到优化算法固然在一定程度山可以找到最优解,但是算法时间复杂度过大;Ping Li[5]提出在近邻传播算法的迭代过程中增加两个指标,动态改变偏向参数的值(APAP).近邻传播算法不需要事先指定聚类个数,但是为了使得聚类结果尽可能与真实情况保持一致,可以事先指定聚类的个数k来约束近邻传播算法,Wang Y[8],Zhang X[9]提出事先指定k个簇,来对近邻传播算法进行约束.

本文针对上述提到的问题,提出了GKAAP算法.首先,通过灰色狼群算法在传统AP算法迭代过程中动态调整偏向参数;然后,根据新的偏向参数,通过二分查找算法实时的调整偏向参数的搜索区间,接着利用当前的吸引度和归属度信息继续迭代;最后由于聚类的个数无法与准确的类数保持一致,所以通过事先指定数据集的真实簇数k来对聚类结果进行约束调整.上述提到的PAAP,GS/GA-AP,CAAP并没有从时间维度和簇个数维度来考量算法的优劣,仅仅从聚类准确率的维度来考量.而本文提出的改进算法(GKAAP)不仅从聚类准确性的层面考虑,又基于算法时间复杂度的层面考虑.通过对比实验的综合比较,GKAAP算法相比AP,AAP,PAAP,GS/GA-AP,CAAP具有更好的性能.

2 近邻传播算法(AP)

近邻传播聚类算法不需要事先指定聚类的中心点,把所有的样本点作为候选聚类中心点.近邻传播聚类算法主要利用数据集中任意两个样本点之间的相似度进行迭代计算.其中相似度的定义为两个样本点之间欧式距离平方的负数,计算相似度矩阵的公式如下:

s(i,j)=-‖xi-xj‖

(1)

在近邻传播算法中需要设置偏向参数的值,默认设置为相似度矩阵的均值,即p=median(s).该算法在计算过程中引入了归属度矩阵A(Availability)和吸引度矩阵R(Responsibility),在算法迭代过程中两个信息矩阵不断的迭代更新.其中:A=(a(i,j))m×n,a(i,j)是样本点j向样本点i发送的信息值,表示为样本点i选择样本点j作为聚类中心点的合适程度;R=(r(i,j))m×n,r(i,j)是样本点i向样本点j发送的信息值,表示为样本点j作为样本点i聚类中心点的合适程度.归属度矩阵和吸引度矩阵的迭代更新的计算公式如下:

r(i,k)=s(i,k)-max{a(i,j)+s(i,j)}j∈{1,2,…,N|j≠k}

(2)

r(k,k)=p(k)-max{a(k,j)+s(k,j)}j∈{1,2,…,N,j≠k}

(3)

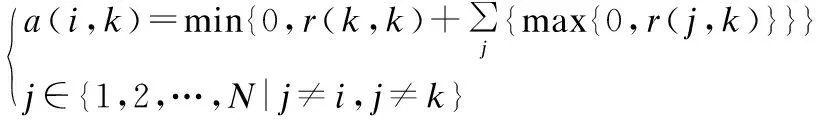
(4)

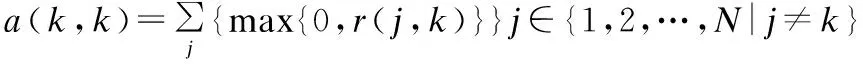
(5)

在计算归属度矩阵相似度矩阵过程中,为了防止震荡,引入了阻尼因子λ来增强算法的稳定性,计算公式如下:

r(i,k)(t+1)=λ.r(i,k)(t)+(1-λ)·r(i,k)(t-1)

(6)

a(i,k)(t+1)=λ.a(i,k)(t)+(1-λ)·a(i,k)(t-1)

(7)

根据以上公式迭代计算归属度矩阵和吸引度矩阵,最终使得聚类目标函数最大化,其中聚类目标函数如下:

(8)

式(8)中,ci为样本点i的聚类中心点,C是由ci组成的向量,i=1,2,…,N(N为样本点个数),S(C)为所有样本点到各自的聚类中心点的相似度之和.其中δk(C)计算公式如下:

(9)

此式为一致性约束惩罚项,如果有某个样本点i选择k作为其聚类中心点,即ci=k,那么样本点k必定选择自身为聚类中心点,即ck=k,否则函数取值-∞,使得样本点i在下次迭代中不再选择样本点k作为自身的聚类中心点.

迭代结束之后通过计算A+R的值来确定聚类中心点,当(r(k,k)+a(k,k))>0时,样本点k即为聚类中心点.各个样本点的聚类中心点ci的计算公式如下:

(10)

该式表示为每个样本点选择归属度和吸引度加和最大的聚类中心点作为自身的聚类中心点.

3 灰色狼群算法(GWO)

3.1 算法描述

Mirialili于2014年提出了GWO算法.在GWO优化算法中,种群中当前最优个体记为α,第二优和第三优的个体分别记为β和δ,剩余个体记为ω,猎物的位置对应于全局最优解.在捕食过程中,通过式(12)对猎物进行包围:

D=|2.r1.Xp(t)-X(t)|

(11)

其中,2.r1为摆动因子(r1为[0,1]之间的随机数),Xp(t)为第t次猎物的位置,X(t)为第t次灰狼个体的位置.利用式(13)对灰狼位置进行更新:

X(t+1)=Xp(t)-A.D

(12)

其中,A为收敛因子,A=2.a.r2-a,r2为[0,1]之间的随机数,a随着迭代次数线性递减到0.

由式(14)计算出α、β、δ与其他灰狼个体的距离,然后由式(15)计算出个体向猎物移动的方向:

(13)

(14)

3.2 GWO算法的优势

GWO算法是灵感来自灰狼的元启发式算法.灰狼算法通过比较得到各个灰狼社会等级提出了三个候选解决方案,用来获取更优值.灰狼算法通过狼群和食物的位置来控制搜索方向,更好的提高了算法的优化效率.与其他进化算法相比,GWO算法的种群之间具有更好的信息共享能力,该算法需调整的参数较少,避免了针对各种问题人工调整参数的繁琐,更好的适用于各种目标函数.为了评估GWO的优化能力,本文对比了遗传算法(GA),粒子群算法(PSO),萤火虫算法(FA),布谷鸟算法(CS),蝙蝠算法(BA).表1给出了五个benchmark测试函数,其中D为维数,fmin为最优的.对比实验见图1到图3.

对比实验见图1到图3.

表1 三个benchmark测试函数Table 1 Three test functions of benchmark

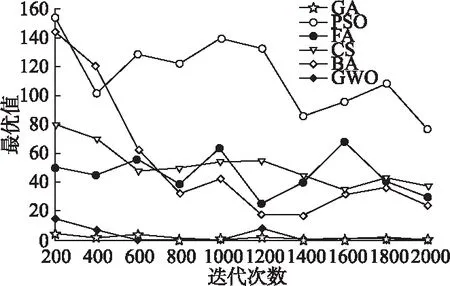
图1 测试函数F1的对比图Fig.1 Comparison chart of the test function F1

图2 测试函数F2的对比图Fig.2 Comparison chart of the test function F2

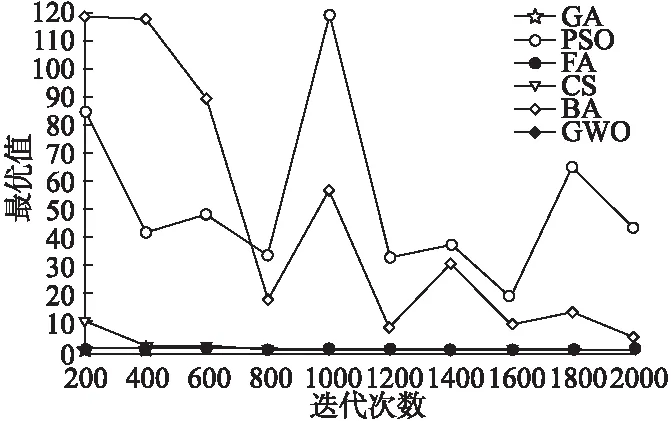
图3 测试函数F3的对比图Fig.3 Comparison chart of the test function F3

benchmark测试函数是群体智能算法测试的通用性函数,具有较强的可信性,其中,迭代次数从200次增加到2000次.从对比结果可以看出,GA、PSO、FA、CS、BA算法在求解最优值时都有较大的波动,而通过GWO算法求解的五个测试函数的最优值几乎都处于0值附近,F1函数在迭代200次、400次和1200次时,GA要好于GWO,在其他迭代次数时,GWO最优;F2函数在所有迭代次数中,FA和GWO都是最优,但GWO要略好于FA;F3函数在所有迭代次数中,GA、FA、CS、GWO四种方法非常接近,都要优于PSO和BA.从三组对比实验来看,GWO算法相比其他进化算法拥有较强的全局搜索能力.

4 GKAAP算法

4.1 算法描述

从3.2中可知GWO算法相对其他算法的优势,AP算法的偏向参数可以作为GWO算法种群的位置,在初始化种群的位置后,进行迭代,在迭代过程中根据新调整的偏向参数去计算Fitness,用Fitness去比较α、β、δ个体的值,同时去更新种群中该三个最优个体的位置,同时计算出种群的搜索方向,最终会搜索出最优的位置,即AP算法中的偏向参数.所以本文算法利用灰色狼群优化算法的思想去动态调整偏向参数.

为了保证实验的效果更好,偏向参数需要在合理的范围内浮动,根据实验观察,当偏向参数的范围为[10pm～0.1pm]时,实验效果更好.其中pm为相似度矩阵的均值.

在随机选取种群之后,挑选其中最优个体的位置作为算法的初始输入.在迭代过程中,当归属度矩阵(A)和吸引度矩阵(R)更新之后,利用灰色狼群优化算法调整偏向参数.在此算法中,偏向参数的值作为灰色狼群算法的一维输入,灰狼的位置X(t)以及猎物的位置D都通过偏向参数来计算.

调整偏向参数之后,为了加快搜寻更合理的偏向参数,需要对偏向参数的搜索区间进行调整.本文利用二分查找算法思想来动态调整搜索区间,通过当前的偏向参数与中间值、上限、下限的比较来调整搜索区间.如果新调整的偏向参数p在[plb～pmid]范围内,并且f(pmid)>f(pub),则有pub=pmid;如果p在[pmid～pub]范围内,并且f(pmid)>f(plb),则有plb=pmid;如果p在[pmid-r～pmid+r]范围内,则搜索区间不变.然后更新pmid,pmid=p,更新之后,进入下一次迭代.

其中,plb为搜索区间的下限,pmid为搜索区间的中间值,pub为搜索区间的上限,r为浮动系数,本文设置为0.05,f为适应度函数.调整区间之后,以当前的r(i,j)和a(i,j)作为起点,继续下次的迭代,直到迭代终止.

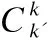
(15)

K′′=K′-K

(16)

其中ε为阈值,本文设置为20,当k′>ε时,K为全集K′,可以防止k′过大,影响程序的性能.

然后根据样本点之间的相似度,分别计算出集合K′′与K中最接近的样本点Cm,同时合并两个类簇,最接近的样本点Cm的计算公式如下:

(17)

其中,k为集合K元素的个数,T为迭代次数,本文设置为100,S(Cil,Ci)为样本点Cil和样本点Ci的相似程度.在计算出最接近点Cm后,更新Cil的标签,同时生成临时的聚类标签组合idx′,当算法迭代k′′(集合K′′的元素个数)次之后,最终形成新的标签组合idx′,如果f(idx′)>f(idx),则有idx=idx′,反之,idx=idx.

综上所述,算法的伪代码见表2.

表2 GKAAP算法Table 2 Algorithm of GKAAP

4.2 适应度函数选取

在采用灰狼调整偏向参数时,适应度函数的选取至关重要,本文选取兰德指数(Rand index,RI)作为适应度函数,兰德指数可以通过原始标签和聚类标签来计算最终的聚类性能.兰德指数计算公式(13):

(18)

其中,f00表示数据点具有不同的类标签并且属于不同类的配对点数目;f11表示数据点具有相同的类标签并且属于同一类的配对点数目,N表示整个数据样本的总量大小.RI取值范围为[0,1],值越大意味着聚类算法的性能越优越.

文献[1,2,3,4]中提到轮廓系数(Silhouette)作为适应度函数,轮廓系数计算公式如下:

(19)

a(t)为聚类Cj中的样本点t与Cj内所有其他样本点的平均距离,b(t)=min{d(t,Ci)},Sill为第l簇的silhouette.其中,i=1,2,…,Ki≠j,d(t,Cj)为Cj的样本点t到另一个类Ci的所有样本点的平均距离.

从公式(18)中可以看出轮廓系数引入了样本点之间的距离,而不同的数据集适用于不同的距离计算规则,所以很难用一个统一的方式去计算轮廓系数.同时从公式(17)、(18)可以看出兰德指数是有标签的评价指标,而轮廓系数是无标签的评价指标,经过大量实验证明有标签的评价指标要优于无标签的评价指标.所以经过分析以兰德指数(RI)作为适应度函数更加合适.

4.3 偏向参数调整分析

本文在3.2通过测试函数验证了灰狼算法有较强的全局搜索能力.为了验证GKAAP算法在搜索偏向参数时,同样具有很好的全局搜索能力.本文选取2个UCI数据集和ORL来对比其他五个算法.为了避免算法的随机性,对比实验都运行10次,取均值.对比结果见图4到图6.纵坐标p是偏向参数,内侧标注的数字为偏向参数对应的类数.

图4 Wine数据集的对比图Fig.4 Comparison chart of Wine data set

图中p_lower是最优偏向参数区间的下限,p_upper是最优偏向参数区间的上限.其中p_lower和p_upper是经过大量的人工实验得到的.

从图4可以看出,AP、AAP、PAAP均没有在最优的区间内,PAAP有3次靠近最优区间边缘,CAAP和GS/GA-AP均有1次在最优区间内,而GKAAP则有6次在最优区间内.

从图5可以看出,其他五个算法均没有在最优区间内,AAP、PAAP、CAAP、GS/GA-AP均比AP更靠近最优区间的边缘,而GKAAP则有9次在最优区间内.

图5 Soybean数据集的对比图Fig.5 Comparison chart of Soybean data set

从图6看出,AP和AAP均没有在最优区间内,PAAP有3次在最优区间内,GS/GA-AP有2次在最优区间内,GKAAP有5次在最优区间内,而CAAP则全部在最优区间内.图6中最优区间的范围很小,说明在搜索时达到范围边缘时需要进行局部搜索,CAAP局部搜索能力要优于GKAAP,但是GKAAP的局部搜索能力还是要明显优于其他四种算法.从这三个对比实验可以看出,在搜索近邻传播算法偏向参数时,本文提出的GKAAP算法具有更强的全局搜索能力.

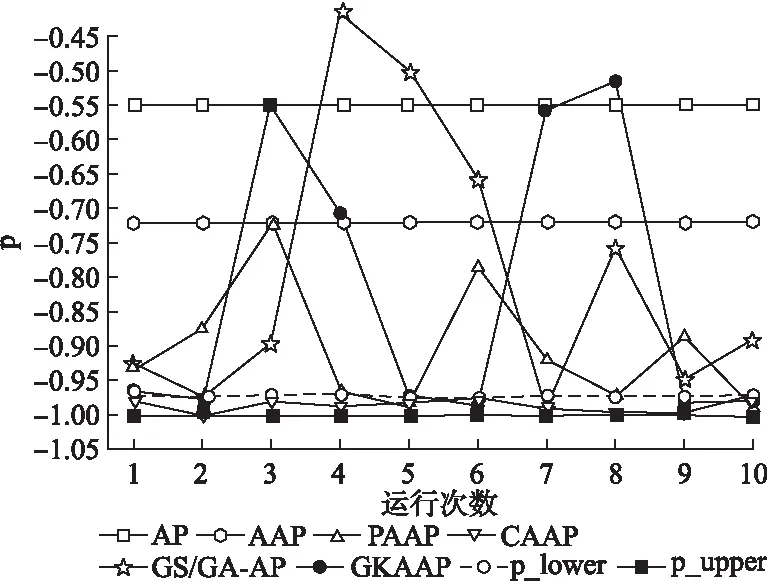
图6 ORL数据集的对比图Fig.6 Comparison chart of ORL data set

5 实验结果与分析

不同指标往往具有不同的量纲和单位,这样会影响数据分析的结果,为了消除指标之间的量纲的影响,本文对数据集进行了归一化处理.本文选取了11个数据集,其中10个UCI数据集和ORL人脸数据库.数据集信息见表3及图7.其中,ORL人脸库由剑桥大学AT&T实验室创建.该库由40位志愿者,每人10幅图像组成,每张图像分辨率为112×92,人脸的尺度有10°的变化,深度旋转和平面旋转可达20°.

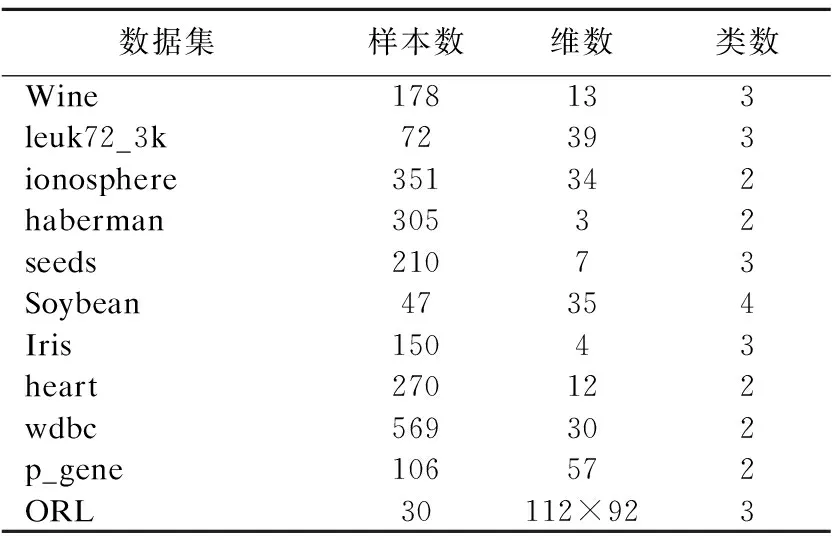
表3 数据集信息Table 3 Information of data set

图7 三组ORL人脸示意图Fig.7 Map of three groups of ORL faces

5.1 评价指标

为了更加客观的反映聚类算法的优劣,本文选取F-Measure作为算法的评价指标,F-Measure是由precision(精确率)和recall(召回率)共同表示,准确率(F-Measure)通常用来表示聚类准确性的优劣.计算公式如下:

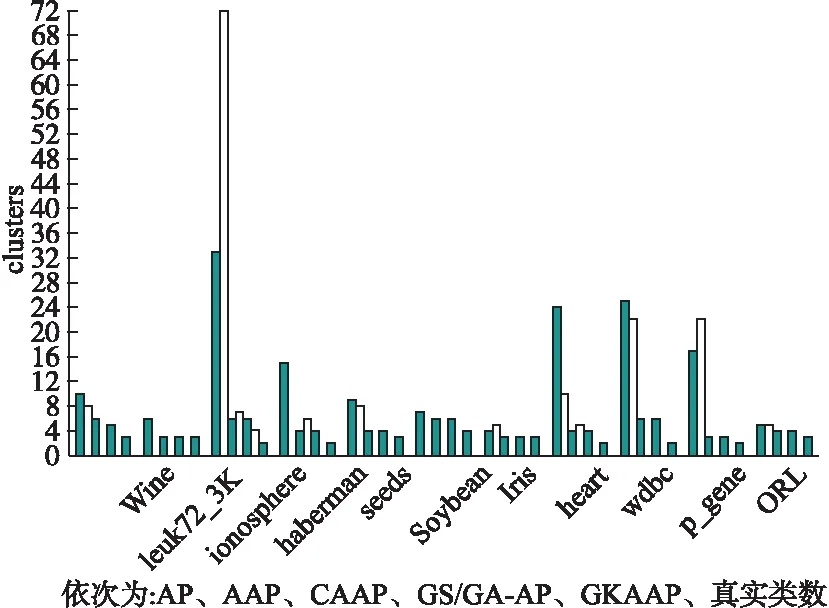
图8 六种方法聚类类数与真实类数对比图Fig.8 Comparison chart of six kinds of clusters with real

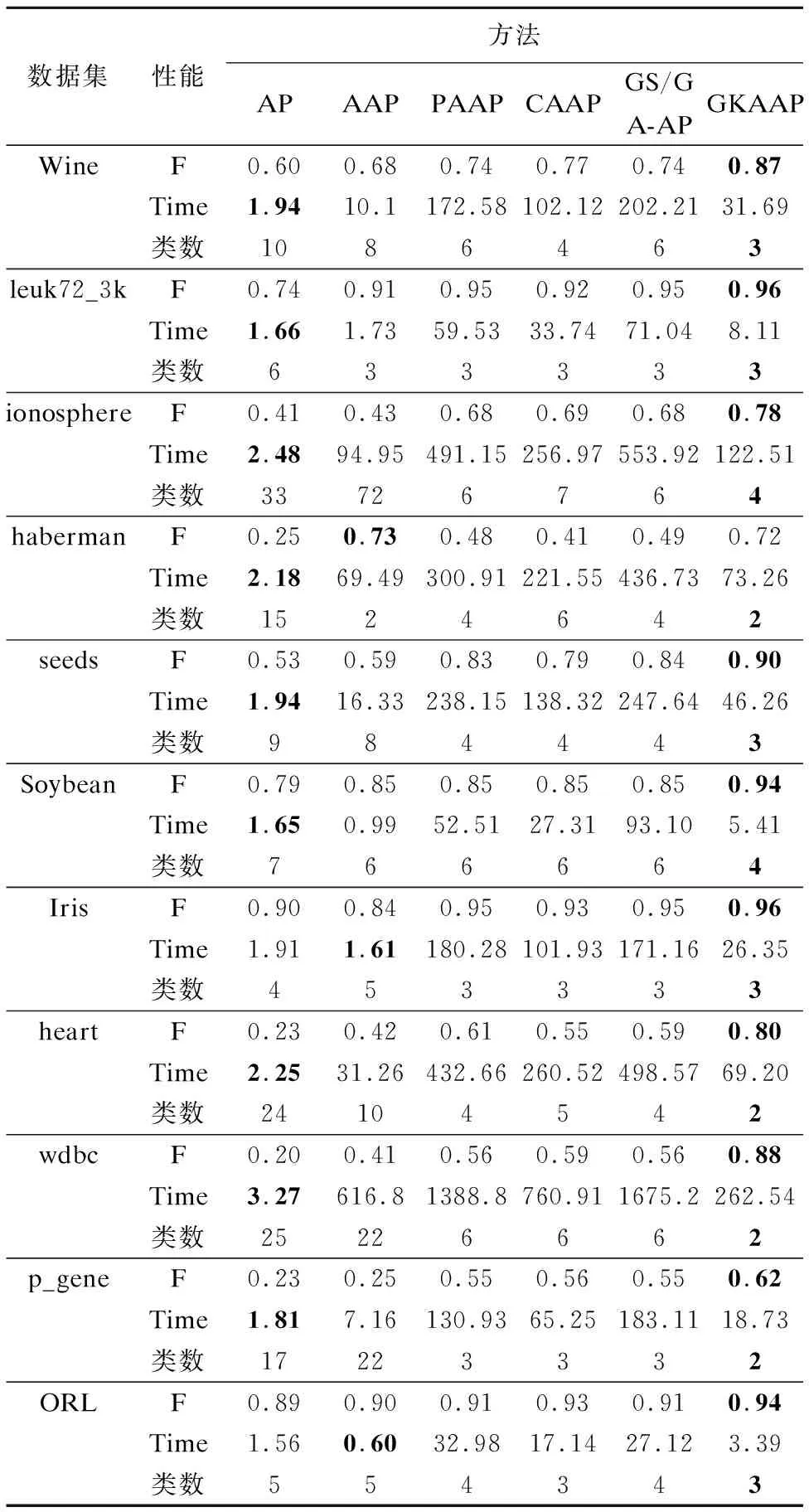
表4 F-measure、时间、类数对比表Table 4 Table chart of F-measure,Time,clusters

(20)

5.2 准确率、时间、类数分析

本文从准确率、时间、聚类类数三个维度对AP,AAP,PAAP,CAAP,GS/GA-AP,GKAAP做了对比.实验为了避免算法的随机性,每个算法运行10次,取均值.其中,F为准确率(F-measure),Time单位为秒(S).表4为数据对比,图8为六种方法的聚类类数与真实类数的对比.

从准确率来看,GKAAP算法在这11个数据集上,相比其他5种算法有了明显的提升,虽然在haberman数据集上AAP算法要好于GKAAP,但是GKAAP在该数据集要明显优于其他通过进化算法改进的AP.

从算法运行时间来看,由于原始AP算法没有动态调整偏向参数所以在算法运行时间上要好于其他算法.AP,AAP,GKAAP的算法时间复杂度都为O(T),其中,GKAAP需要考虑优化偏向参数时适应度函数的计算时间,所以在运行时间上要多于AP,AAP.但GKAAP算法相比PAAP、CAAP、GS/GA-AP等通过进化算法改进的算法还是有了明显的缩短,PAAP,CAAP,GS/GA-AP算法时间复杂度为O(T.N),由于在调整新的偏向参数后利用当前的A和R的值,会加快算法的收敛,所以在时间复杂度上要优于PAAP,CAAP,GS/GA-AP.

从聚类类数以及图8的对比来看,GKAAP算法的聚类相比其他五种算法更接近真实的类数.在ionosphere数据集上当偏向参数减少到类数为4时,准确率为最好,如果继续减少则准确率下降,所以GKAAP算法在该数据集的最终结果的类数要多于真实类数,但是比其他算法更接近真实类数.从4.2可知,本文算法在调整偏向参数时,总是可以找到最优的偏向参数.在输出聚类结果之后,通过指定数据集的簇数对聚类结果进行约束调整使得聚类结果的类数和准确率更好.最后从聚类准确率、算法运行时间、聚类类数这三个维度来看,本文提出的GKAAP算法显然性能是最优的.

5.3 效果图分析

为了能够更加直观地看出六种聚类算法优劣,本文通过聚类效果图展示的形式,来更加直观的反映表4数据的有效性.为了更好的显示聚类效果,本文通过PCA将数据集降至2维,从而可以在二维平面上显示最终的聚类结果.本文选取Wine数据集做效果图展示的对比.

其中Wine数据集有178个样本点,13维属性,3类数据,其对比效果见图9到图14.

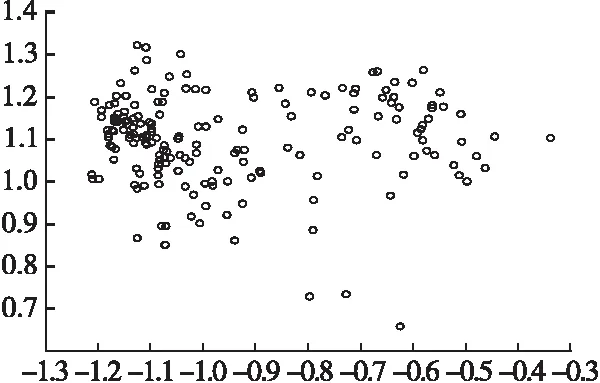
图9 原始数据集分布图Fig.9 Raw dataset distribution

图10 Wine通过原始AP算法聚类效果图Fig.10 Clustering effect map of Wine by AP

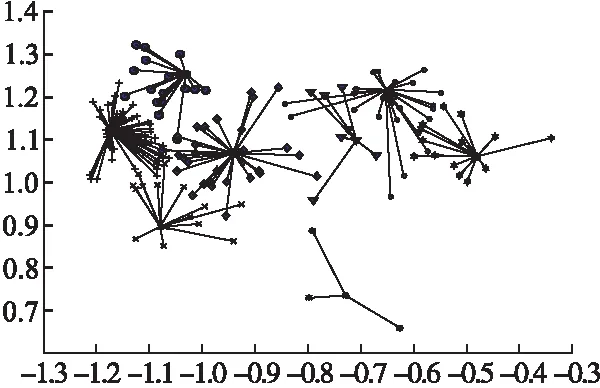
图11 Wine通过AAP算法聚类效果图Fig.11 Clustering effect map of Wine by AAP

由图9-图14知,AP聚10类,AAP聚8类,PAAP和GS/GA-AP均聚6类,CAAP聚4类,而GKAAP聚3类，与Wine的类数相符，且聚类后样本点分布的区域与原始数据集分布很接近,区域密度也类似,类与类间很少交叉.AP、AAP、PAAP、CAAP、GS/GA-AP都有3个点被作为孤立点,被单独聚为一类.证明这几种方法在处理一些边缘数据点时效果很差.

图12 Wine通过PAAP和GS/GA-AP算法聚类效果图Fig.12 Clustering effect map of Wine by PAAP or GS/GA-AP

图13 Wine通过CAAP算法聚类效果图Fig.13 Clustering effect map of Wine by CAAP

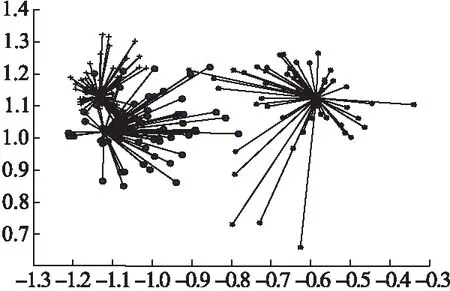
图14 Wine通过GKAAP算法聚类效果图Fig.14 Clustering effect map of Wine by GKAAP

从图中直观地看出GKAAP算法对传统AP算法有明显改进,同时相比较本文中提到其他的改进算法也有明显的改进，结合表4的数据分析说明GKAAP具有很好的聚类性能.

6 结束语

本文介绍了近邻传播(AP)和灰色狼群(GWO)的原理与步骤,同时介绍了通过指定的数据集簇数进行约束调整的方法.然后对基于灰色狼群算法自适应调整偏向参数(GKAAP)的问题进行建模和求解.最后在UCI数据集和ORL人脸数据库上进行了对比实验.证明了本文所研究的方法既能有效的调节偏向参数,找出最优的偏向参数,同时使得最终的聚类与真实类数更加的接近,又能相比其他优化算法缩短运行时间,使得最终的聚类效果达到更优.

：

[1] Wang K,Zhang J,Li D,et al.Adaptive affinity propagation clustering[J].Acta Automatica Sinica,2007,33(12):1242-1246.

[2] Wang X,Qin Z,Zhang X.Automatically affinity propagation clustering using particle swarm[J].Journal of Computers,2010,5(11):1731-1738.

[3] Jia B,Yu B,Wu Q,et al.Adaptive affinity propagation method based on improved cuckoo search[J].Knowledge-Based Systems,2017,111(C):27-35.

[4] Jiao L,Zhang G,Wang S,et al.Optimal preference detection based on golden section and genetic algorithm for affinity propagation clustering[J].International Journal of Distributed Sensor Networks,2015,9204 (64):253-262.

[5] Li P,Ji H,Wang B,et al.Adjustable preference affinity propagation clustering[J].Pattern Recognition Letters,2016,85(420):72-78.

[6] Hang W,Chung F L,Wang S.Transfer affinity propagation-based clustering[J].Information Sciences,2016,348(1176):337-356.

[7] Wang C D,Lai J H,Suen C Y,et al.Multi-exemplar affinity propagation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2013,35(9):2223-2237.

[8] Wang Y,Chen L.K-MEAP:Multiple exemplars affinity propagation with specified K clusters[J].IEEE Transactions on Neural Networks and Learning Systems,2015,27(12):1-13.

[9] Zhang X,Wang W,Norvag K,et al.K-AP:generating specified K clusters by efficient affinity propagation[C].IEEE International Conference on Data Mining (ICDM),2010 IEEE 10th International Conference on IEEE,2010:1187-1192.

[10] Wei Z,Wang Y,He S,et al.A novel intelligent method for bearing fault diagnosis based on affinity propagation clustering and adaptive feature selection[J].Knowledge-Based Systems,2017,116(C):1-12.

[11] Emary E,Zawbaa H M,Grosan C.Experienced gray wolf optimization through reinforcement learning and neural networks[J].IEEE Transactions on Neural Networks and Learning Systems,2017,PP(99):1-14.

[12] Li L,Sun L,Guo J,et al.Modified discrete grey wolf optimizer algorithm for multilevel image thresholding[J].Computational Intelligence and Neuroscience,2017,(285-296):1-16.

[13] Bose P,Douïeb K,Iacono J,et al.The power and limitations of static binary search trees with lazy finger[J].Algorithmica,2016,76(4):1264-1275 |.

[14] Kim S,Heo K,Oh H,et al.Widening with thresholds via binary search[J].Software:Practice and Experience,2015,46(10):1318-1328.

[15] Jiang J,Huang J,Wang X R,et al.Investigating key genes associated with ovarian cancer by integrating affinity propagation clustering and mutual information network analysis[J].European Review for Medical and Pharmacological Sciences,2016,20(12):2532-2540.

[16] Zhou Shi-bing,Xu Zhen-yuan,Tang Xu-qing.A method for determining the optimal number of clusters based on affinity propagation clustering[J].Kongzhi Yu Juece/control & Decision,2011,26(8):1147-1152.

[17] Xu Ming-liang,Wang Shi-tong,Hang Wen-long.A semi-supervised affinity propagation clustering method with homogeneity constraint[J].Acta Automatica Sinica,2015(2):255-269.

[18] Xiao Yu,Yu Jian.Semi-supervised clustering based on affinity propagation algorithm[J].Journal of Software,2008,19(11):2803-2813.

附中文参考文献：

[16] 周世兵,徐振源,唐旭清.一种基于近邻传播算法的最佳聚类数确定方法[J].控制与决策,2011,26(8):1147-1152.

[17] 徐明亮,王士同,杭文龙.一种基于同类约束的半监督近邻反射传播聚类方法[J].自动化学报,2015(2):255-269.

[18] 肖 宇,于 剑.基于近邻传播算法的半监督聚类[J].软件学报,2008,19(11):2803-2813.