基于密度峰值的云变换加速机制

杨 洁，王国胤，庞紫玲

1(重庆邮电大学 计算智能重庆市重点实验室，重庆 400065)

2(遵义师范学院 物理与电子科学学院，贵州 遵义 563002)

1 引 言

粒计算[1]是基于多层次粒结构研究思维方式、问题求解方法、信息处理模式的理论.早在1997年，Zadeh教授[2]就提出了粒计算是模糊信息粒化、粗糙集理论和区间计算的超集，是粒数学的子集.粒计算并不是个具体的计算理论模型或方法，而是一种方法论.在粒计算的“大伞”之下，粒计算包含了很多具体的粒化模型，如模糊集[2]、粗糙集[3]、商空间[4]、云模型[5]等.这几种粒化模型分别从不同的角度描述人类从不同粒度解决问题的能力，有着严谨的约束条件，但是同时也具有一定的局限性.

云模型[5]是李德毅院士于1995年在概率论和模糊理论两者的基础上提出的定性概念与其定量表现形式的双向转换模型.其中，正向云变换(Forward Cloud Transformation，FCT)和逆向云变换(Backward Cloud Transformation，BCT)是实现双向认知变换的重要工具.如图1所示，通过FCT和BCT，云模型可以实现内涵与外延的双向转换.

图1 云模型双向认知转换图Fig.1 Bidirectional cognitive transformation of cloud model

与其他粒化模型对信息的硬划分不同，由于定性概念的外延往往是不确定的、模糊的、变化的，涉及到随机性和模糊性两种不确定性，云模型将模糊理论与概率论相结合，通过三个特征参数：(Ex，En，He)，可以度量一个定性概念的信息粒度，可以实现对信息的软划分.其中，Ex代表期望，可以作为概念粒度的基本确定性衡量；En代表熵，可以作为粒度的不确定性度量，由概念的随机性和模糊性共同决定;He代表超熵，可以将定性概念的随机性约束弱化为某种“泛正态分布”，反映定性概念所对应的随机变量偏离正态分布的程度.通过En和He可以构建概念含混度用来衡量概念的共识程度，为一个基本概念的表征，计算和度量提供了基础.由于这种粒化方式考虑了数据的概率分布，获取的知识具有更强的泛化能力，而且利用云模型进行粒化不需要先验知识，它可以从原始数据中统计规律，实现定量到定性概念的转换.

自适应高斯云变换 (Adaptive Gaussian cloud transform，AGCT)[6]，是众多云模型粒计算机制中最为合理的一种方法.AGCT可以根据不确定性概念在不同粒度层次上的不同表现形式，建立了一种多粒度的推理模型与方法，该方法直接从数据中获得不同粒度层次的云概念，从数据拟合的角度实现了从细粒度概念到粗粒度概念的跃升.但AGCT只能通过逐层学习达到概念层次跃升.当数据样本较庞大时，采用逐层变粒度的方法必然比较耗时，时间复杂度为O(m2N)，其中m为初始波峰数,N为样本个数.因此，AGCT很难满足时限约束条件下的变粒度有效计算.如果能利用关键信息粒进行加速计算，实现跨层的变粒度机制，那么对于概念的提取将在很大程度上减少时间的损耗.

2014年在《Science》发表的论文“Clustering by fast search and find of density peaks[7]，DPC”(密度峰值聚类)提出的局部密度和相对距离这两个假设能够有效、快速的发现任意形状的簇.该方法融合K-medoids[8]，DBSCAN[9]和mean-shift[10]聚类的特点，简洁新颖.密度峰值算法的提出引起学界广泛关注，并且已经应用于许多领域，包括图像中人物的年龄估计[11]、计算机视觉中的基础矩阵估计[12]、分析化学[13]、社交网络[14].因此，DPC新颖而简洁思路可以为我们解决AGCT时间复杂度过高的问题提供思路.

本文第2节简要介绍了密度峰值、高斯云变换的一些基本知识，并分析了AGCT存在的问题.第3节围绕这些基本问题，分析了利用密度峰值的思想改进AGCT的可行性并给出改进算法；第4节通过实验验证了改进算法的优越性；最后是研究展望与总结.

2 相关定义

2.1 密度峰值聚类

密度峰值聚类算法的核心思想在对于聚类中心的刻画上.文献[7]认为聚类中心同时具有以下两个特点：

1)本身的密度大，即被比它密度小的邻居点包围；

2)与比它密度更大的数据点之间的距离相对更大.

在这样的模型中，密度峰值聚类主要有两个需要计算的量：第一，局部密度ρ；第二，相对距离δ.局部密度和相对距离的定义分别如下：

定义1[7].样本点i的局部密度，定义如下

(1)

其中

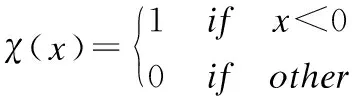
定义2[7].样本点i的相对距离

(2)

其中，指标集

如图2(a)所示，为二维散点图，其中样本点编号代表自身的局部密度，不同的颜色代表不同的类.图2(b)为以局部密度为横坐标和相对距离为纵坐标产生的图2(a)的数据对应的决策图，决策图为我们提供了一种手动选取聚类中心的启发式方法.在图2(b)中选择局部密度ρ和相对距离δ同时相对较大的(矩形虚线内的点)，由于这些点的密度较大，邻域中的邻居点较多，并且与比它密度更大的点的距离较远，所以将这些点标记聚类中心.

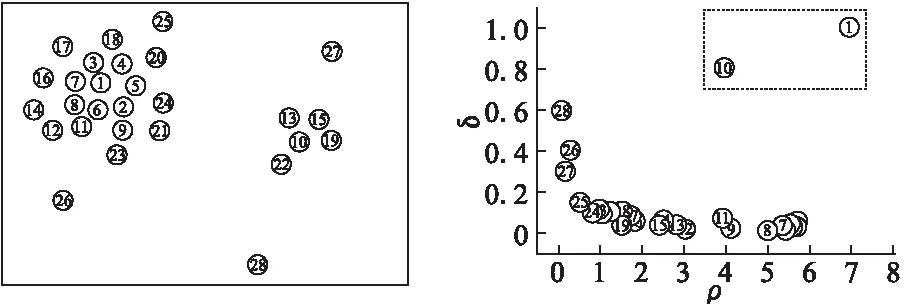
图2 中心点选取例子Fig.2 Example of choosing centers

2.2 高斯云变换

概念层次在数据挖掘中有着重要的作用.通过自动生成概念层次，可有效地提高数据挖掘的效率，在不同层次上发现知识[15].由于数据库中大量存在各种数值型属性，传统的一些概念层次生成算法[16-18]都只能对论域进行硬划分，并不能很好的反映数据的分布状况.同时，这些算法都只能生成概念树，且概念爬升比较机械，不能反映定性概念的模糊性、随机性以及不同层次概念之间的多隶属关系.由于基于云模型的粒化方式考虑了数据的概率分布，获取的知识具有更强的泛化能力.因此，结合虚拟泛概念树的跃升原理，建立多层次、多粒度的概念外延空间成为云模型研究的一个方向.

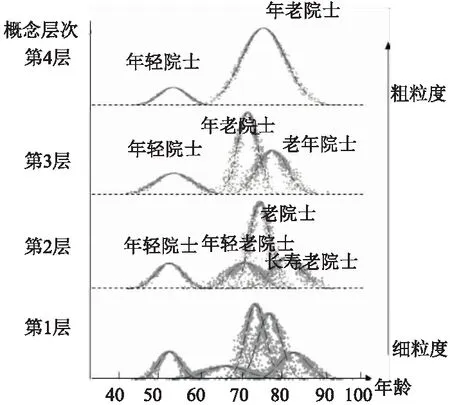
图3 AGCT对院士群体聚类形成的多粒度概念[6]Fig.3 Multi-granularity concepts of academician group by AGCT

刘玉超和李德毅等[6]根据不确定性概念在不同粒度层次上的不同表现形式，提出了自适应高斯云变换(AGCT)，建立了一种多粒度的推理模型与方法，该方法直接从数据中获得不同粒度层次的云概念，从数据拟合的角度实现了从细粒度概念到粗粒度概念的跃升.图3为利用AGCT对中国工程院院士群体进行云变换得到的不同概念层次.

因此，高斯云变换是一个聚类的过程，也是一个变粒度计算的过程，甚至可以说是一个深度学习的过程.与单纯的逆向云算法比较，对于任意一个给定的数据集而言，难以仅用一个定性概念来描述，则通过高斯云变换可生成多个不同粒度的概念，这比用逆向云算法生成的单个概念更具有普遍性.

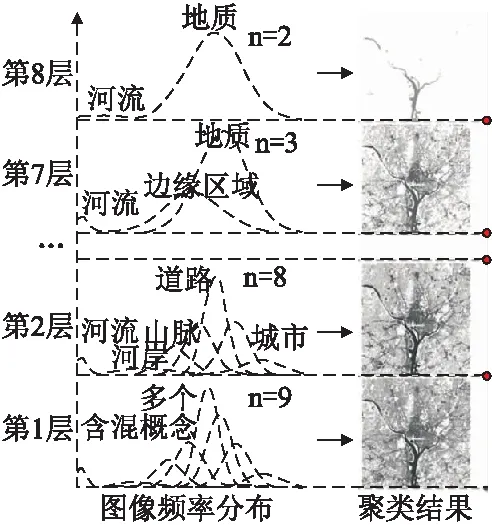
图4 利用AGCT进行粒度空间优化Fig.4 Granular optimization by AGCT

图4展示了一个利用AGCT实现粒度空间优化的例子，通过实际约束条件调节概念含混度，可以实现不同粒度层次上对遥感图像进行图像分割，使其不同的概念层次具有不同的分割结果，最终提取符合人类认知的概念个数，从而实现了概念数量，粒层和层次的生成，选择和优化问题.

3 基于密度峰值的云变换加速机制

3.1 跨层机制

面对大数据分析带来的挑战，数据分析的重心从算法的研究转移到数据表达模型的研究.以往的计算方法以算法为中心，重点在于降低算法的时间复杂度，但在大数据环境下，即使是具有较低时间复杂度的算法仍然难以保证计算的有效性.将计算方法转变为以数据为中心，研究变粒度机制，可以实现数据的多粒度表达，做到将数据规模变小，从而提供“有效”计算.其中，利用关键信息粒加速计算可以再很大程度上减少不必要的时间损耗，其目的是在较低粒层上依据信息粒的价值度量识别出关键信息粒，由其状态的改变，直接触发高层信息粒的改变，实现跨层机制，从而做出决策，采取行动，为建立满足时限约束条件的变粒度有效计算模型提供条件.

如图5所示的整个粒空间结构中，Layerk表示最细粒度的粒层，其中各个小圆点代表最细粒度数据，具有同类关系的数据构成信息粒.Layert是粒空间结构中的某一粒层，通过利用该层中关键信息粒实现跨层机制，从而无需经过Layers层直接跃升到Layerr层，在一定程度上减少了变粒度过程所需的时间.

3.2 自适应云变换加速机制

由第2.1节可知，基于对聚类中心点的假设，密度峰值聚类算法可以快速寻找中心点，但是要寻找中心点必须要计算每个样本点的局部密度，而计算局部密度的距离矩阵代价时间复杂度较大，需要O(N2).AGCT根据数据样本的的频度来进行数据拟合，通过去抖动后得到波峰数及其位置信息分别作为初始云模型的数目和期望，文献[6]认为数据样本点的频率与其对概念的贡献度成正比，即高频率的数据对概念的贡献较大；反之，低频率的数据对概念的贡献较小.受密度峰值聚类思想启发，对于灰度直方图来说，那些频度相对较大且离比它频度大的点相对远的数据点才是概念的主要贡献点.因此，在AGCT算法中，通过选取这样的数据点为初始云概念提供先验知识，可以很大程度上降低云变换的时间复杂度.

图5 跨层机制示意图Fig.5 Schematic of cross layer mechanism

本文基于自适应高斯云变换通过统计样本频度进行云变换的原理，借鉴密度峰值的思想，通过遍历计算每个样本点的频度，把它们各自的频度当成是DPC中的局部密度来快速寻找中心点，为AGCT的初始峰值的选取提供先验信息，直接从细粒度跃升到较粗粒度上面进行变粒度机制，从而实现云变换加速机制.由于距离矩阵是基于论域的，而通常情况下，尤其是对于图像来说，论域的取值范围远远小于样本点个数，因此，计算论域取值之间的距离代价也相对较小.该算法在保证概念抽象精度的前提下，从很大程度上减少时间复杂度.如算法1所示，为本文基于密度峰值提出的启发式云变换加速机制(Heuristic Gaussian Cloud Transfromation based on Density peaks，HGCT_DP)

算法1.基于密度峰值的启发式云变换(HGCT_DP)

输入：数据样本集X{xi|i=1，2，…，N}的频率直方图p(xi)以及论域{yj|j=1，2，…，N′}

输出：m个高斯云C(Exk，Enk，Hek)|k=1，2，…，m′

①根据p(xi)计算论域中每个取值yj的频度ρi以及相对距离δj；

②通过p(xi)和δj输出决策图，选取聚类中心centerk|k=1，2，…，m，并记录这个m个点的信息，作为概念数量的初始值.

③将②中m个中心点的信息作为高斯变换的输入，并转换成m个高斯分布；

G(μk，δk)|k=1，2，…，m′

④对于第k个高斯分布，计算其标准差的缩放比αk，则第k个表征概念的高斯云参数为：

Exk=μk

Enk=(1+αk)*σk/2

Hek=(1-αk)*σk/6

CDk=(1-αk)/(1+αk)

从而得到k个云模型.

在算法1中，m′的选取我们采用冗余法，选取3～5倍直观中心点的个数.

算法2.自适应云变换加速机制(AGCT_acc)

输入：数据样本集X{xi|i=1，2，…，N}，概念含混度阈值β

输出：M个高斯云模型

① 统计数据样本集X{xi|i=1，2，…，N}的频率直方图p(xi)

②利用HGCT_DP算法将数据集X{xi|i=1，2，…，N}聚类成m个高斯云C(Exk，Enk，Hek)|k=1，2，…，m′；

③ 按含混度顺序，对每m个高斯云的含混度CD进行判断，如果CDk>β，k=1，2，…，m′，则概念数m′=m′-1，跳转至②；否则，输出M个含混度小于等于β的高斯云：

C(Exk，Enk，Hek)|k=1，2，…，M

由算法2可知，本文提出的AGCT_acc通过直接在较粗粒度上进行概念跃升，虽然减少了时间复杂度，同时也减少了逐层学习的次数，但较AGCT而言，AGCT_acc的精度未必会损失很大，尤其是当数据集规模较大时，可以在保证精度的前提下从很大程度上减少时间损耗，对于实际应用是有必要的.图6为利用AGCT_acc对两张不同的图片进行云变换时对应的决策图以及最终生成的云概念.我们利用AGCT_acc在大量数据集上进行概念抽象得到初始中心点个数的经验值约为显著点个数(图6(b)为2个，图6(e) 为4个)的3～5倍.

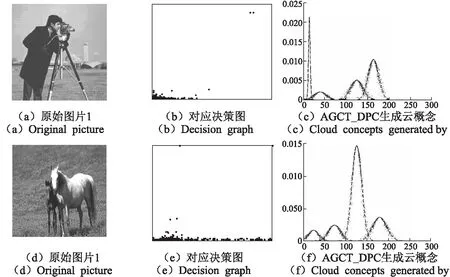
图6 不同图片对应的AGCT_acc的决策图及其云概念Fig.6 Decision graph and cloud concepts of different pictures by AGCT_DPC

由于本文采用的统计论域是每个取值的频度，并把频度当成是DPC中的局部密度来计算.因此，假设论域有N′个取值，则计算距离矩阵时间复杂度为O(N′2).由于N′=N，所以O(N′2)可以忽略不计.再者，由于通过DPC的思想可以为AGCT的初始峰值的选取提供先验信息，从而可以直接从较粗粒度上面实现概念跃升.假设初始选取m′个峰值点，则AGCT_acc总的时间复杂度为O(N′2)+O(m′2N)≈O(m′2N)，其中N为数据样本点个数.由第1节分析可知，AGCT的时间复杂度约为O(m2N)，由于m′2≼m2，所以O(m′2N)≼O(m2N).因此，AGCT_acc的时间复杂度远低于AGCT.

4 实验仿真分析

本实验的硬件配置为Intel i5-2430M的CPU，8G内存，操作系统为Windows7 64bit OS的台式机，采用MATLAB2014软件进行仿真.

4.1 图像分割中过渡区发现

人类不仅能从有确定目标的图像中获取知识，而且可以从不确定目标的图像提取概念，但这些不确定图像传递的信息是模糊的，不能直观的进行理解，而这些信息往往在某些领域(工业、空间探测、医学等)又是比较重要的.基于云模型在处理不确定性以及双向认知方面所具有的优势，本文以工业中常见的激光熔覆图像为例，对这类图像进行分割，以提取出所符合认知的目标概念.

激光熔覆图是一种新的表面改性技术，在工业中具有广泛的应用前景.在该工艺中，如何从激光熔覆图像获取精确的激光高度是关键点之一[19].如果只考虑图像的灰度值属性，那么图7 (a)显示了一幅256×256像素、灰度值在[0，255]之间的激光熔覆图，白色区域为高能密度的激光，黑色区域为背景颜色，同时在前景和背景之间存在一个过渡区域.以图像中像素点的灰度值作为数据集合，通过采用本文提出的AGCT_acc算法对图像进行概念提取的结果，得到3个概念如表1所示.

图7(b)A为GCT算法对激光熔覆图进行分割得到的三色图；图7 (c)为IS-IE算法[19](基于粗糙直方图的云模型图像分割算法)所获得的三个概念所对应的三色图，图7 (d)为AGCT_acc算法所获得的三个概念所对应的三色图，其中灰色部分对应概念C1，黑色部分为概念C2，白色部分为概念C3.实验证明，本文提出的AGCT_acc算法也能对激光熔覆图的三个区域同时进行划分，而且不确定性区域较小，从直观上更符合人的认知特点.但由于对此类实验结果当前不存在衡量标准，因此这里不将三种算法得到的三色图进行数据上的对比.

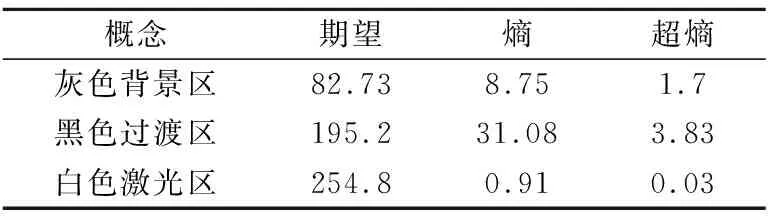
表1 AGCT_acc图5(a)上聚类形成的3个概念Table 1 Comparison of two granularity concepts

图7 AGCT、IS-IE与AGCT_acc分割结果对比Fig.7 Comparison of segmentation results by AGCT，S-IE and AGCT_acc

4.2 多粒度图像分割

由于文献[6]已经通过验证了AGCT算法在图像分割方面的性能，因此，本文着重对比提出的算法AGCT_acc与AGCT两种算法在多粒度图像分割的效果和时间损耗上的差异.

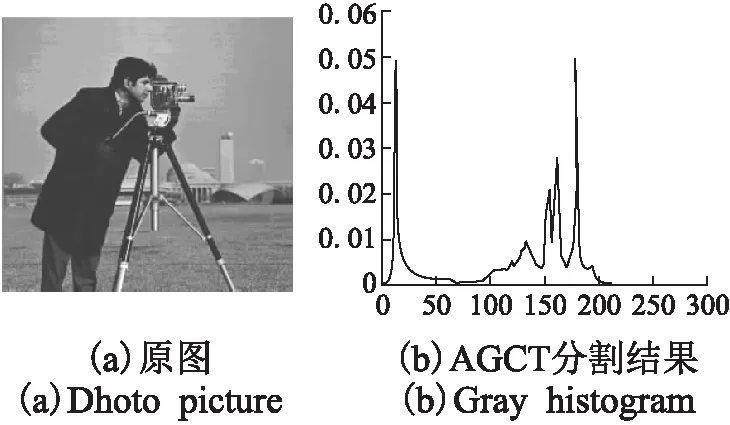
图8 一幅灰度特征明显的photo图像Fig.8 A photo image with distinct gray features

如图8所示，图8 (a)是一幅图像分割中的经典图像，直观上感觉图像从大尺度上应分为两类，因为人和相机明显区别于其他背景信息.图像的其灰度直方图如图8(b)，本文以图8(a)为实验对象，分别利用AGCT_acc与AGCT对对图8(a)进行概念抽象，形成不同粒度、不同层次的云概念，从不同粒度对图像进行分割，从分割效果和时间损耗两方面对AGCT_acc与AGCT两种方法进行对比.

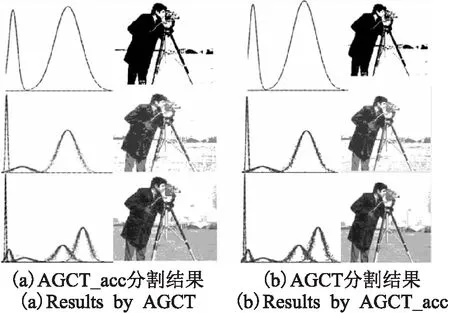
图9 AGCT_acc与AGCT变粒度对比图Fig.9 Comparison of variable granularity by AGCT_acc and AGCT

如图9所示，为AGCT_acc与AGCT变粒度对比图，从上至下，依次采用概念外围区不交叠、基本区不交叠、骨干区不交叠的粒度变换策略，基于AGCT_acc与AGCT的图像分割先从大尺度对全局信息进行粗粒度分割，形成整体上划分的两个概念，再从较细度上发现相机支架、草地等局部特征信息，最后对天空、远处建筑等区域进行较细粒度的划分.从图中可以看出，AGCT_acc与AGCT的分割效果基本上是一致的.

表2 AGCT_acc与AGCT在图8(a)=上聚类形成的2个粒度概念对比Table 2 Comparison of two granularity concepts generated on fig.8(a) by AGCT_acc and AGCT

表2、表3和表4分别给出了不同粒度对应的云概念参数以及时间损耗，可以看出AGCT_acc比AGCT形成同一粒度上云概念的时间损耗非常接近，从而保证了两种方法在图8(a)的分割效果一致.

表3 AGCT_acc与AGCT在图8 (a)上聚类形成的3个粒度概念对比Table 3 Comparison of three granularity concepts generated on fig.8 (a) by AGCT_acc and AGCT

5 展望与总结

作为一种简单有效的数据分析方法，密度峰值聚类算法思想新颖而简洁，通过算法的假设条件可以快速寻找中心点.基于高斯云变换统计样本频度进行概念跃升的特点，本文利用密度峰值的思想提出一种云变换加速机制，用于加速高斯云变换中变粒度过程，实现概念的快速跃升，并从理论上证明本文提出的AGCT_acc算法的时间复杂度远小于AGCT.通过图片数据集上的实验显示，进一步验证了本文提出的算法的时间损耗远低于AGCT.虽然AGCT_acc减少了逐层学习的次数，但得到的概念与AGCT非常相似，即精度并未很大程度的损耗.总结全文，我们认为本文提出的算法还可以从以下几个方面进行深入研究：

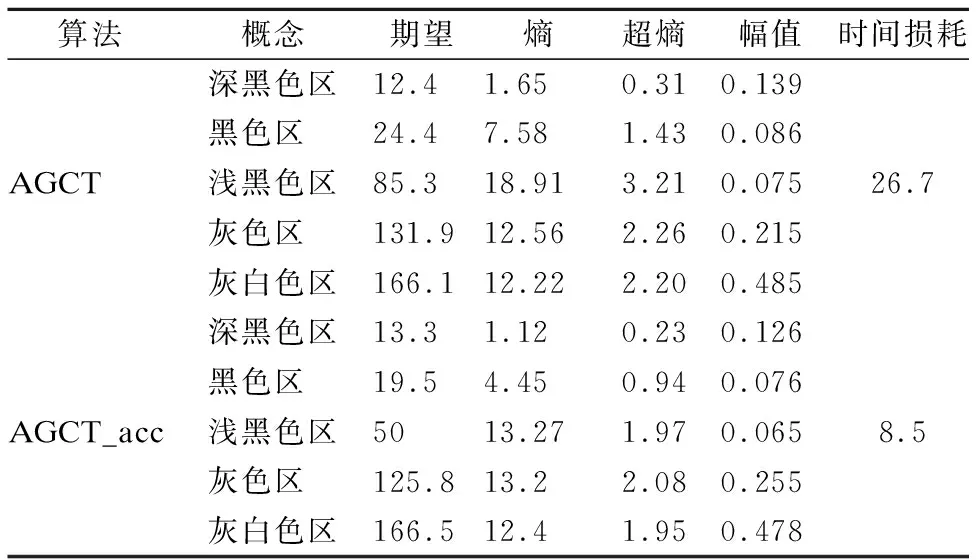
表4 AGCT_acc与AGCT在图8 (a)上聚类形成的5个粒度概念对比Table 4 Comparison of five granularity concepts generated on fig.8 (a) by AGCT_acc and AGCT

1)本文提出的AGCT_acc算法的不足之处之一是在选取中心点个数时需要人的参与，即该算法是启发式算法，因此有必要研究如何利用密度峰值聚类算法中样本点γ值(γ=δ*ρ)的渐变关系自适应选取中心点以及获取中心点个数，使AGCT_acc算法自适应化.

2)高斯云变换以高斯混合模型为基础，保证其数学理论上的科学性和严谨性，从特定问题出发，通过调节概念含混度优化概念数目，粒度大小，层次关系等，可以模拟人类认知中的变粒度过程[6].目前的高斯云变换只能实现从细粒度到粗粒度的合成机制，无法实现从粗粒度到细粒度的分解机制.如果能实现分解机制，对于某些特定的情形可以避免云模型迭代次数过高的问题，从而进一步降低时间复杂度.

：

[1] Pedrycz W.Granular computing：analysis and design of intelligent systems[M].CRC Press，2013.

[2] Zadeh L A.Fuzzy sets[J].Information & Control ( Inf & Contr)，1965，8(65)：338-353.

[3] Pawlak Z.Rough sets[J].International Journal of Computer & Information Sciences，1982，11(5)：341-356.

[4] Zhang Yan-ping，Zhang Ling，Wu Tao.The representation of different granular worlds：a quotient space[J].Chinese Journal of Computers，2004，27(3)：328-333.

[5] Li De-yi，Meng Hai-jun.Membership and membership cloud generator[J].Journal of Computer Research and Development，1995，32(6)：15-20.

[6] Liu Y C，Li D Y，He W，et al.Granular computing based on gaussian cloud transformation[J].Fundamenta Informaticae，2013，127(14)：385-398.

[7] Rodriguez A，Laio A.Machine learning clustering by fast search and find of density peaks[J].Science，2014，344(6191)：1492-1496.

[8] Park H S，Jun C H.A simple and fast algorithm for K-medoids clustering[J].Expert Systems with Applications (Expert Syst Appl)，2009，36(2)：3336-3341.

[9] Saragih J M，Lucey S，Cohn J F.Deformable model fitting by regularized landmark mean-shift[J].International Journal of Computer Vision，2011，91(2)：200-215.

[10] Sun K，Geng X，Ji L.Exemplar component analysis：a fast band selection method for hyperspectral imagery[J].IEEE Geoscience & Remote Sensing Letters (IEEE Geosci Remote S)，2015，12(5)：998-1002.

[11] Chen Y W，Lai D H，Qi H，et al.A new method to estimate ages of facial image for large database[J].Multimedia Tools & Applications，2016，75(5)：1-19.

[12] Wu H，Wan Y.Clustering assisted fundamental matrix estimation[J].Computer Science，2015.

[13] Dean K M，Davis L M，Lubbeck J L，et al.High-speed multiparameter photophysical analyses of fluorophore libraries[J].Analytical Chemistry，2015，87(10)：5026-5030.

[14] Wang M，Zuo W，Wang Y.An improved density peaks-based clustering method for social circle discovery in social networks[J].Neurocomputing，2015，179(29)：219-227.

[15] Jiang Rong，Li De-yi，Fan Jian-hua.An automatic generation method for the generalized concept tree of numerical data[J].Chinese Journal of Computers，2000，23(5)：470-476.

[16] Cheung D，Fu A，Han J.Knowledge discovery in databases：arule-based attribute-oriented approach[C].Proceedings of the International Symposum on M ethodologies for Intelligent Systems，Charlotte，NC，1994：164-173.

[17] Lu Y.Concept hierarchy in data mining：specification，generation and implementation[D].Simon Fraser University，1997.

[18] Han J，Fu Y.Discovery of multiple-level association rules from large databases[C].Proceeding of the 21st VLDB Conference，Zurich,Swizevland,1995.

[19] Yao Hong.Research on image segmentation method based on the concept of connotation and denotation bidirectional cognitive transformation[D].Chongqing：Chongqing University of Posts and Telecommunications，2013.

附中文参考文献：

[4] 张燕平，张 铃，吴 涛.不同粒度世界的描述法—商空间法[J].计算机学报，2004，27(3)：328-333.

[5] 李德毅，孟海军.隶属云和隶属云发生器[J].计算机研究与发展，1995，32(6)：15-20.

[15] 蒋 嵘，李德毅，范建华.数值型数据的泛概念树的自动生成方法[J].计算机学报，2000，23(5)：470-476.

[19] 姚 红.基于概念内涵与外延双向认知变换的图像分割方法研究[D].重庆：重庆邮电大学，2013.