一种基于高斯混合模型、结合拓扑与内容的大规模社团发现方法
罗国华,龚欣哲,王英奎,何东晓,金 弟
(天津大学 计算机科学与技术学院,天津 300350)
1 引 言
社团结构是复杂网络中最重要的拓扑属性之一,具有“同一社团内之结点相互连接紧密、不同社团间之结点相互连接稀疏”之特点[1].社团发现的目的就是要探测出复杂网络中具有的社团结构,可帮助人们理解复杂网络的功能、发现复杂网络中隐藏的规律、预测复杂网络的行为等.它不仅吸引了大量不同学科的研究工作者,而且已被应用于如:恐怖组织识别、组织结构管理、蛋白质功能预测、搜索引擎等诸多领域[2,3].
对复杂网络的社团结构挖掘是一个十分经典的研究课题,已经有很多先前的相关研究,早期的研究方法主要有图分割法,聚类方法和谱分析法几种,而这些研究方法基本上都与图论有关,图论是一种简单明了又具有很大研究空间的数学学科分支,是由数学家欧拉开创的一项重要的工作.现在已经在计算机科学界拥有巨大的研究价值.人们对网络的研究经历了几个阶段,从开始的规则网络中节点之间关系的研究,到后来的随机网络中节点间关系的研究,直到现在的复杂网络中关系的研究,都离不开图论.
关于复杂网络中进行社团发现的问题,目前已经有了许多种解法,大致上分为两类:
1)忽略内容信息而更加关注处理网络中的拓扑性以及拓展性问题.
2)同时关注内容信息以及拓扑信息.从本质上来看,第二种方式是在第一种方法的基础上的提高,因为内容信息可以为提升推断社团的质量提供帮助.但是这种方法在网络的扩展时,会面临更多的成本问题[4].
为了能够在网络中发现社团结构,研究者们做出了许多努力.在接下来的研究中,一些研究者们专注于研究在连接关系上的社团划分,这是由社团结构的直观定义:社团结构是一种内部连接紧密而与外部连接稀疏的结构来得出的方法.这方面的算法根据采用的技术或理论的不同,它们主要可以分为:凝聚或分裂算法[5]、基于模块度优化的方法[6]、谱方法[7]、动力学方法[8]等.
上述方法只是利用的链接关系而忽略网络中每个节点所含有的内容信息,导致在一些问题中,划分结果不能反映每个聚类中的主题关系.在一些社团发现问题,如推荐好友时,内容信息是十分重要的,如果只考虑连接关系的话,就只能够找到与用户关系最为密切的好友,但无法找到和用户所关注的兴趣爱好最为相近的好友.所以同时利用网络中节点的拓扑连接关系与内容信息来发现社团的方法也在不断地被更多人所重视.
同样的,也有许多利用内容信息帮助发现社团的研究,其中之一的方法就是概率生成模型,这是一种基于一个或多个潜变量,结合内容和拓扑连接,估计条件分布来寻找社区分配的方法.例如:Leskovec 等[9]同时利用网络拓扑与结点属性,提出了一个可扩展性的重叠社团检测算法.基于结点隶属每个社团的概率,首先面向网络拓扑构建概率生成模型;然后针对结点的属性构建Logistic模型;最后合并两个模型,并采用极大似然估计求解.Yu 等[10]通过把原始网络转化为“结点-链接”交互(NEI)图,将网络拓扑、结点上的内容和链接上的内容有效融合;通过在每一步更新的NEI 图上采用异步随机游走方法,动态检测网络社团结构.
面对如今规模越来越大的网络数据,对图像进行采样再进行聚类的方法越来越吸引人们的注意力,如果一个图结构中的边界经过采样变得尽可能的少,那么社团发现算法就能够用更少的空间、占据更小的存储空间来得出与原图经过社团发现算法操作后相近的结果.2013年,Ruan 等人提出了基于TF-IDF方法的,对于网络中节点的内容信息进行处理,以达到结合拓扑与内容进行社团发现的目的的CODICIL算法[4].该算法中的TF-IDF方法维度过高,不能够准确的描述每个节点内容信息的特征情况,并且计算量十分庞大.对此,本文基于此算法,使用高斯混合模型(GMM)拟合结合网络中拓扑结构以及节点内容信息的社团发现算法,通过在真实世界网络数据集中的比较,表明这一算法相对于只考虑网络中的拓扑信息的社团发现算法,可以比较好的在网络中进行社团发现,且在精度和速度上比原算法优越.
2 方 法
一个图结构可以被分为三个部分:图中的节点,图中的边和图中每个节点所代表的内容信息.我们定义符号ζt=(V,εt,T)来表示图,其中,ζt表示有n个节点V=v1,v2,…,vn的集合,而在图中会存在t条连接节点与节点间边εt.同时,由于每个节点有其节点本身所含有的内容信息,而这些内容信息可以被看作一个向量,我们称其为词向量(term vectors)或者内容向量(content vectors),每个节点的会含有n个内容向量T=t1,t2,…,tn.他们一起构成了我们整个算法所需要的网络.我们需要在这个网络中对内容向量进行处理,生成每个节点内容最相近的邻居节点,将他们之间生成一条内容边后,与网络中原有拓扑边进行结合,经过采样之后,进行社团发现.
2.1 创建内容边
在本文中,我们将使用高斯混合模型(Gaussian mixture model),来拟合图ζt=(V,εt,T)中每个点相对于每个聚类的关系.使用由数个不同的高斯模型混合组成的高斯混合模型来拟合的原因是通过高斯分布的线性组合,可以拟合相当复杂的概率密度形式.如果使用的高斯分布足够多,几乎可以拟合所有的连续概率密度.
我们使用了R语言中的Flexmix软件包来实现高斯混合模型算法(GMM).Flexmix包是R的扩展包之一,它提供方法来使用EM算法和模型选择来拟合有限混合模型[14].也就是说,不仅是我们目前使用的高斯模型之间可以进行拟合,如伯努利模型,二次模型等模型之间都可以进行互相拟合.有限混合模型是由K个不同的成分的凸组合(wiki)得出的.即权重非负且和为1.Flexmix包使用规则如下:
flexmix(formula,data=list(),k= NULL,cluster = NULL,
model = NULL,concomitant = NULL,
control = NULL,weights = NULL)
使用此软件包得出的结果是经GMM方法拟合出图ζt=(V,εt,T)中每个点相对于每个聚类关系的N×K(N节点,K类)概率矩阵A,我们通过向量之间的相似性计算方法,计算出每两个节点之间的内容相似度.一般来说,我们经常使用的是余弦相似度(cosine similarity)方法,即:
(1)
通过余弦相似度方法所得出的每个节点vi相似度最大的k(k=50)个邻居vj,我们将他们所构成的一条边(vi,vj),添加到内容边集合εc中.
此方法相对于TF-IDF方法能体现出两个优越性:
1)能使最后的聚类结果精度提高;因为GMM方法本身就是比较成熟且精度高的聚类算法,而TF-IDF不能够准确的描述每个节点内容信息的特征情况;所以最后的结果的精度相应的提高.
2)计算速度的提高;TF-IDF方法维度过高(N×N),计算量十分庞大,而GMM方法使得为N×K的矩阵A,K类的数量是远小于N节点的数量的,所以维度的大幅度降低,使得计算速度的提高.
2.2 对边集合进行采样
我们在上一步创建内容边中,得到了每个节点与其内容上最相似的k个节点,并将他们之间创建一条内容边存在了边集合εc中,而我们原有的数据中,存在有在连接关系上的拓扑网络边集合εt,所以我们的第一步是将这两个集合合并为一个集合,目的是将一些内容上十分相似,但是在拓扑结构上没有联系的节点互相联系起来.最终得到一个总的边集合εu=εc+εt.再将εc,εt分别与εu进行相似度计算,一般我们会使用Jaccard算法:
1http://linqs.cs.umd.edu/projects/projects/lbc/
(2)
(3)
(4)
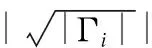
这样,我们通过对集合εu中边的采样,得到了采样后的边集合εsample,我们可以将这些边和没有变动的节点结合一起,组成最后我们的采样结果:一个图结构的网络数据ζsample=(v,εsample).
2.3 聚类划分采样图
得出一个简化的图ζsample后,这样我们就完成了CODICIL算法的核心部分,我们接下来只需要使用EIG以及CNM聚类算法,对我们之前得到的采样结果图ζsample进行聚类,就可以得到一个即考虑了节点之间的拓扑连接信息,也考虑了节点内含有的内容信息的聚类结果.
3 实 验
本实验是基于CODICIL算法在一个网络数据中结合边链接和内容信息进行社团发现的;使用我们提出改进后的高斯混合模型的CODICIL算法得出聚类结果数据,再使用评价函数将这个结果与原TF-IDF的CODICIL算法和只使用拓扑链接数据的聚类效果进行评价.
实验数据1采用的是Cornell,Texas,Washington,CiteSeer和Pubmed Diabetes 五个数据集,例如:CiteSeer数据集是关于学术论文数字图书馆的引文索引数据,数据中的文章被归纳成六类领域,在我们的实验结构图中,每个节点代表每篇文章,无向边代表文章之间的引用关系,每个节点的内容信息则用源于研究文章词汇的二进制向量表示.所有实验均运行于配置为3.70GHz CPU、8核处理器且内存为32GB的windows7机器上,且所有算法均基于R语言和MATLAB实现.
我们实验使用的数据集分为两部分(以CiteSeer为例),一部分为文章(节点)之间的引用关系(链接边)的数据,另一部分为每篇文章对应词汇的二进制特征向量表示的内容特征信息及每篇文章的真实归属6个类领域的聚类.接下来,我们提交给算法处理的数据集,必须被归纳为两个矩阵:一个是数据点之间的拓扑连接矩阵,代表着网络中的拓扑信息(即为CiteSeer数据集的第一部分).另一个是每个数据点的内容向量的集合所组成的矩阵,代表着网络中每个节点的内容信息(即为CiteSeer数据集的第二部分).如果我们的网络中有n个节点,每个节点的内容向量有m项内容特征,那么我们的拓扑连接矩阵就是一个n×n的矩阵,而内容向量矩阵应该是一个n×m的矩阵.所以我们需要将数据集中的每篇文章,即网络中的节点,以序号的方式命名后,用数字的形式替代拓扑文件中的引用关系文章名,而内容向量部分数据集本身不需要我们调整,每篇文章所属的真实数据聚类归属和文章名一样,替换成序号数字的形式.将CiteSeer数据集载入到flexmix软件包的高斯混合模型算法中实现创建内容边:
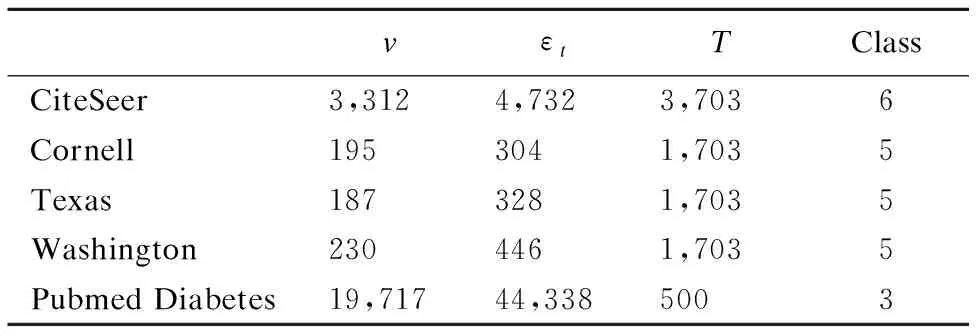
表1 实验数据集ζt=(v,εt,T)Table 1 Experimental data set ζt=(v,εt,T)
R> CiteSeer _mix<-flexmix(matrix~1,
+ data= CiteSeer _content,model=FLXMCmvcombi(),
+ control=list(minprior=0.005),k=6)
R>posterior(CiteSeer _mix)
得出每个节点对应6个类的概率矩阵,对此矩阵进行通过向量之间的相似性计算方法,计算出每两个节点之间的内容相似度.再按照本文第2节所述的方法进行后续的对边集合进行采样和聚类划分采样图步骤得到聚类结果.
在此我们还采用了两种不同的评价函数对拓扑信息和内容结合最终得到的邻接矩阵的聚类结果与我们事先得到的已知聚类归属数据进行精确性比对.评价函数分别是NMI和F-score评价指标.

表2 EIG 函数聚类结果比较Table 2 EIG function clustering results compare
根据实验数据对比,我们可以看出,在绝大多数情况下,无论是在使用EIG聚类函数(表2),或者是使用CNM聚类函数(表3)的情况下,我们改进后的使用高斯混合模型的GMM_CODICIL都比使用TF-IDF的CODICIL算法的聚类效果会更好一些.
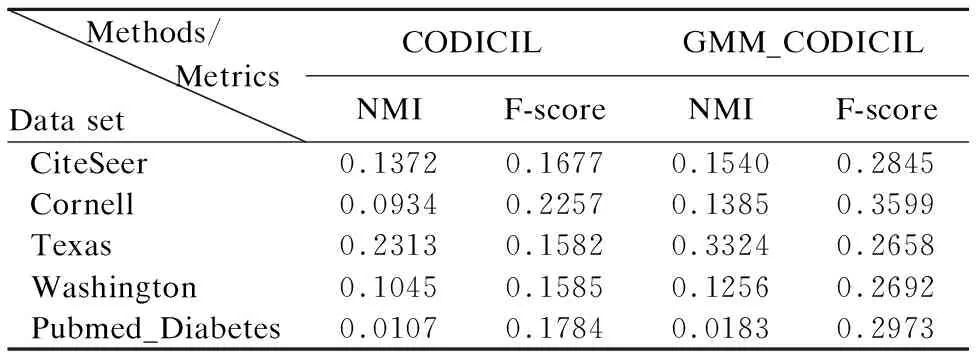
表3 CNM 函数聚类结果比较Table 3 EIG function clustering results compare
同时因为GMM在维度上相对于TF-IDF降低了,所以在计算速度上也明显加快.
4 结 论
本文提出了使用高斯混合模型(GMM),来对原CODICIL算法中,对内容向量中的内容特征进行权重调整的方法进行改进.本文通过分析GMM方法与每个节点的内容向量相对于数个内容聚集中心的内容相似性之间的相似性,得出可以使用EM算法来迭代产生GMM的隐变量期望,从而求得网络中每个节点所带有的内容信息与设定的数个聚集之间的相似度,从而分析出节点的内容信息的倾向.同时基于CODICIL算法,计算出与之前仅包含拓扑信息的网络不同的,兼顾拓扑信息与内容信息的网络数据来进行社团发现,有利于提高社团发现的精确度.最后通过评估实验,验证了算法的准确性和实用性.
我们以后的工作主要有两方面:一方面,将加入语义信息,给打上语义标签,使得在聚类图标中能体现出社团的语义比例信息,从而更直观的表示出聚类社团的信息.另一方面,由于本文方法的运行计算速度快,将本文方法向动态性扩展,应用于动态网络社团挖掘研究领域,并试图从中探测和揭示出具有重要意义的真实网络社团结构.
:
[1] Girvan M,Newman M E J.Community structure in social and biological networks[J].Proc.Natl.Acad.Sci.USA,2002,99(12):7821-7826.
[2] Wang Li,Cheng Xue-qi.Dynamic community in online social networks[J].Chinese Journal of Computers,2015,38(2):219-237.
[3] Johnson N F,Zheng M,Vorobyeva Y,et al.New online ecology of adversarial aggregates:ISIS and beyond[J].Science,2016,352(6292):1459-1463.
[4] Ruan Y Y,Fuhry D,Parthasarathy S.Efficient community detection in large networks using content and links[C].Proceedings of the 22nd International World Wide Web Conference (WWW-13),Rio de Janeiro,Brazil:WWW,2013:1089-1098.
[5] Jia S W,Gao L,Gao Y,et al.Defining and identifying cograph communities in complex networks[J].New Journal of Physics,2015,17(1):013044.
[6] Zhang P,Moore C.Scalable detection of statistically significant communities and hierarchies,using message passing for modularity[J].Proc.Natl.Acad.Sci.USA,2014,111(51):18144-18149.
[7] Li Y X,He K,Bindel D,et al.Uncovering the small community structure in large networks:a local spectral approach[C].Proceedings of the 24th International World Wide Web Conference (WWW-15),Florence,Italy:WWW,2015:658-668.
[8] Rosvall M,Esquivel A V,Lancichinetti A,et al.Memory in network flows and its effects on spreading dynamics and community detection[J].Nature Communications,2014,5(1):4630-4637.
[9] Yang J,McAuley J,Leskovec J.Community detection in networks with node Attributes[C].Proceedings of the IEEE 13th International Conference on Data Mining (ICDM-13),Dallas,Texas:IEEE,2013:1151-1156.
[10] Wang C D,Lai J H,Yu P S.NEIWalk:community discovery in dynamic content-based networks[J].IEEE Trans.Knowl.Data Eng.,2014,26(7):1734-1748.
[11] Liu Da-you,Jin Di,He Dong-xiao,et al.Community mining in complex networks[J].Journal of Computer Research and Development,2013,50(10):2140-2154.
[12] Newman M E J,Clauset A.Structure and inference in annotated networks[J].Nature Communications,2016,7(1):11863-11873.
[13] Wang X,Jin D,Cao X C,et al.Semantic community identification in large attribute networks[C].Proceedings of the 30th AAAI Conference on Artificial Intelligence (AAAI-16),Phoenix,Arizona:AAAI,2016:265-271.
[14] Gruen B,Leisch F,Sarkar D,et al.Flexmix:flexible mixture modeling[EB/OL].https://CRAN.R-project.org/package=flexmix,2015.
附中文参考文献:
[2] 王 莉,程学旗.在线社会网络的动态社区发现及演化[J].计算机学报,2015,38(2):219-237.
[11] 刘大有,金 弟,何东晓,等.复杂网络社团挖掘综述[J].计算机研究与发展,2013,50(10):2140-2154.

